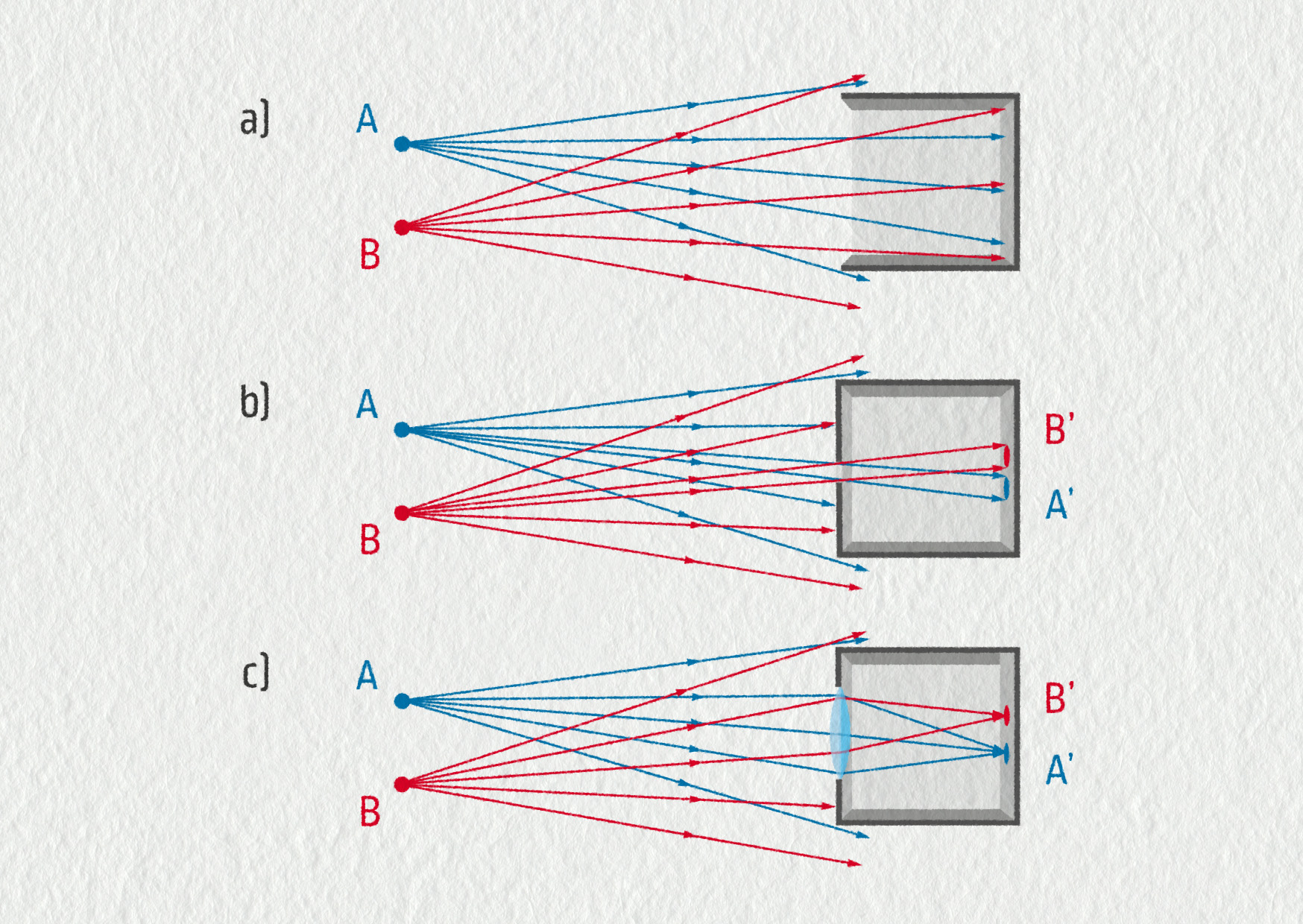
Zobrazení v geometrii je předpis, který určuje jednotlivým bodům (vzorům) jejich obrazy. Například v osové souměrnosti se body zobrazí vždy na kolmici k ose ve stejné vzdálenosti od ní. Zobrazení v optice můžeme chápat jako fyzickou realizaci matematického zobrazení pomocí světla. Při optickém zobrazení se mění chod paprsků tak, že vzniká obraz předmětu v jiném místě prostoru. Pojďme se podívat, jak může takové zobrazení vypadat v praxi. Použijeme k tomu dva bodové zdroje A a B a projekční plochu (stínítko). Tou může být bílý papír, fotografický film, snímač digitálního foťáku nebo sítnice v našem oku. Na obrázku 23.31 část a) vidíme, co se stane, když zdroje umístíme před projekční plochu a necháme paprsky šířit volně prostorem. V tomto případě žádný obraz nevznikne, protože oba zdroje osvětlují celou projekční plochu.
Zdroj
Na obrázku 23.31 část b) vidíme nejjednodušší způsob, jak vytvořit optické zobrazení. Nazývá se dírková komora neboli camera obscura. Před projekční plochu umístíme miniaturní otvor, který odstíní téměř všechny paprsky. Ty, které projdou, vytvoří obrazy bodů na ploše. Tento jednoduchý princip zobrazování byl historickým předchůdcem fotoaparátu. Problém dírkové komory je ten, že otvor musí být velmi malý, aby nedošlo k podstatnému rozmazání obrazu. Díky tomu proniká dovnitř jen minimální množství světla. Pro dokonalé zobrazení, kdy se bod zobrazí přesně na bod, by byl potřeba nekonečně malý (bodový) otvor, který by do komory pouštěl nekonečně málo světla.
Pořádné zobrazovací zařízení proto musí měnit směr chodu paprsků, jak vidíme na obrázku 23.31 část c). Dírku nahradíme skleněnou čočkou ve správné vzdálenosti od projekční plochy. Čočka láme paprsky právě tak, aby se paprsky vycházející z jednoho bodu protly opět v jednom bodě. Říkáme, že v bodě A′ vzniká skutečný obraz bodu A. Tento obraz můžeme pozorovat okem na projekční ploše nebo zachytit na senzor fotoaparátu.
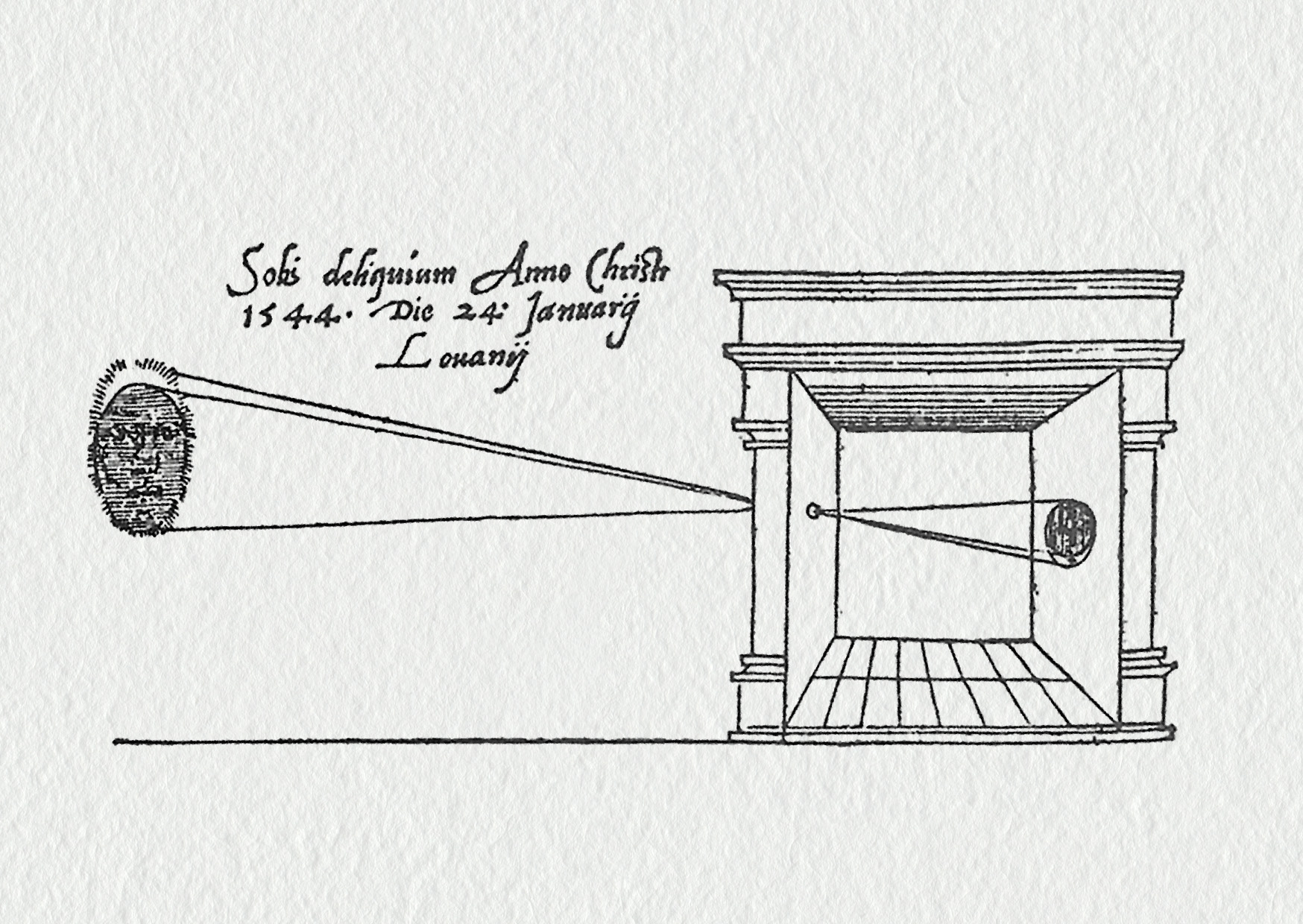
Dírková komora (latinsky camera obscura, anglicky pinhole camera) je jednoduché optické zobrazovací zařízení ve tvaru uzavřené skříňky či prostoru, v jehož jedné stěně je malý otvor, který na protilehlé stěně vytváří obraz vnějšího prostoru (viz obrázek 23.32).
Zdroj
S obrazem vytvořeným malou dírkou se lze setkat v přírodě i v běžném životě a lidé v různých koutech světa ho pozorovali již od pradávna. Například Aristoteles se ve svém díle zamýšlel nad problémem, proč sluneční světlo procházející malým čtyřúhelníkovým otvorem, vytváří kruhový obraz Slunce. Uspokojivou odpověď ale neznal, protože principy geometrické optiky tehdy nebyly známy. Také arabský fyzik a matematik Alhazen v 10. století popisuje převrácený obraz vytvořený malou dírkou. První podrobnější popis dírkové komory najdeme v rukopise Leonarda da Vinciho z konce 15. století. Leonardo ji používal ke studiu perspektivy.
V průběhu 16. století byla camera obscura malou místností, kde se obraz promítal na stěnu otvorem v protilehlé stěně. Byla využívána k pozorování zatmění slunce a ke zkoumání zákonů zobrazování. Později se z ní stal přenosný přístroj a nakonec byla dírka nahrazena spojnou čočkou. Tyto zobrazovací přístroje se používaly jako malířská pomůcka a začátkem 19. století se staly základem konstrukce prvních fotoaparátů.
Přestože technicky je již dírková komora překonaná, stále se najdou umělci a nadšenci, kteří pomocí dírkové komory pořizují fotografie. Vyrobit jednoduchou dírkovou komoru je snadné. Do jedné stěny uzavíratelné krabičky z neprůsvitného materiálu se udělá otvor, na který se umístí kousek slabého plíšku s nepatrnou dírkou. Zvenku se otvor přelepí proužkem černé lepenky. Ta poslouží jako spoušť. Na protější stěnu se ve tmě připevní film nebo fotopapír a fotoaparát je připraven k práci. Pokud byste si chtěli sami vyzkoušet výrobu dírkové komory a dozvědět se víc informací, můžete se inspirovat například na těchto webových stránkách: https://www.pinhole.cz/ nebo podrobnější stránka v angličtině: https://jongrepstad.com/pinhole-photography/.

Zdroj
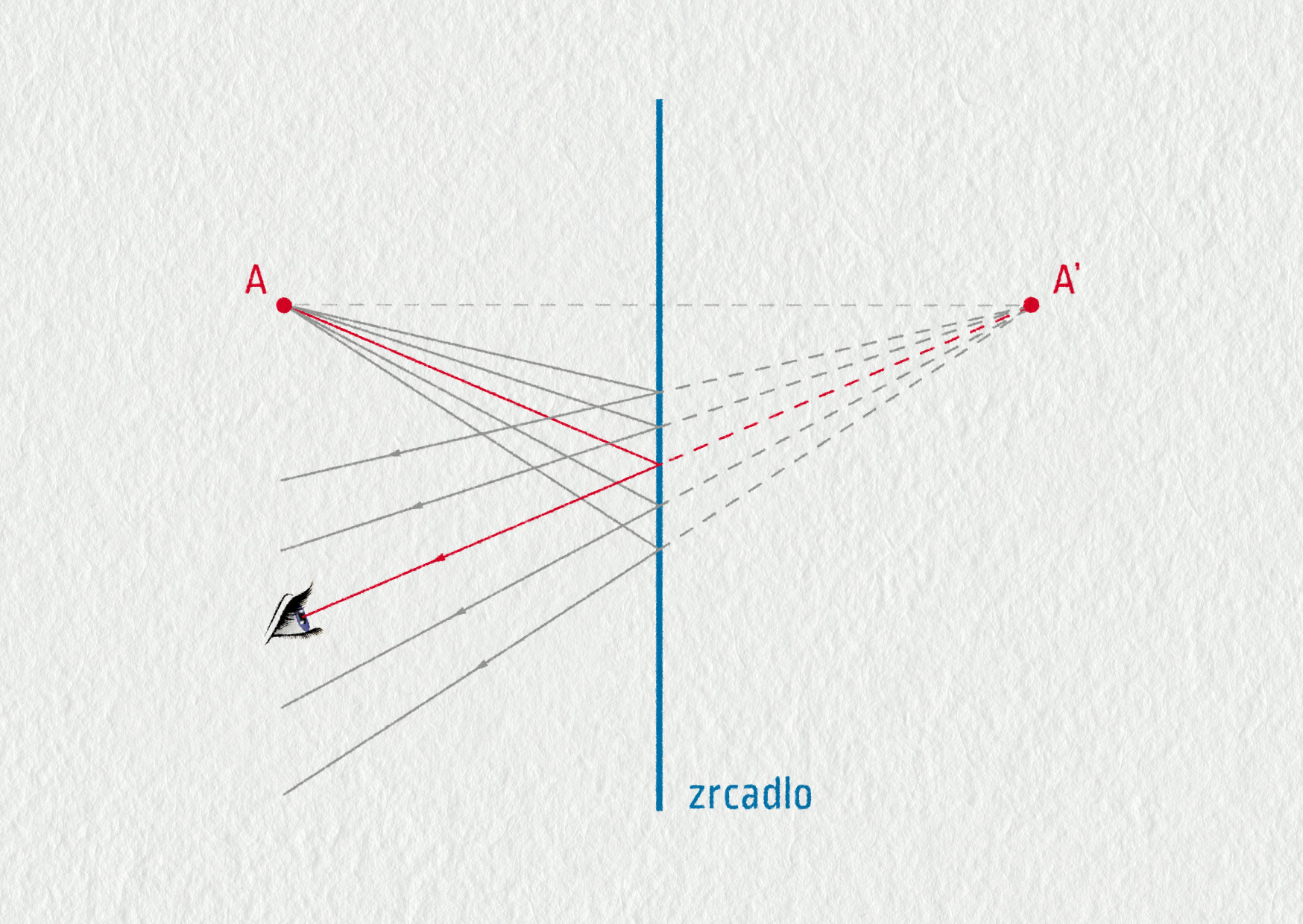
V optice se setkáváme ještě s trochu záhadným pojmem „neskutečný obraz“. K jeho objasnění použijeme obyčejné rovinné zrcadlo. Na obrázku 23.34 vidíte paprsky, jak se odrážejí od zrcadla podle zákona odrazu a některé z nich dopadají do oka pozorovatele. Přestože se bod A nachází před zrcadlem (vlevo), pozorovatel vidí jeho obraz A′ za zrcadlem vpravo. Proč tomu tak je? Oko nemá žádnou informaci o celkovém chodu paprsků prostorem. Určuje polohu předmětu pouze na základě směru, ze kterého přicházejí paprsky. V našem případě oko zaznamená rozbíhavé paprsky, jako by vycházely z bodu A′. Říkáme, že pozorovatel vidí v bodě A′ neskutečný obraz bodu A. Neskutečný obraz bodu je tedy zdánlivý zdroj rozbíhavých paprsků. Jeho polohu najdeme v průsečíku prodloužení rozbíhavých paprsků.
Zdroj
Skutečný obraz bodu = bod, kde se protínají paprsky sbíhavého svazku světla.
Neskutečný obraz bodu = bod, odkud zdánlivě vycházejí paprsky rozbíhavého svazku světla.
Z geometrické konstrukce na obrázku vyplývá, že rovinné zrcadlo vytváří rozbíhavý svazek světla a proto za zrcadlem pozorujeme neskutečný obraz předmětů. Polohu pozorovaného bodu určuje oko vždy výhradně podle směru odkud do něj přicházejí paprsky.
Obrazy bodů při zobrazení rovinným zrcadlem nemusíme složitě rekonstruovat, jako na obrázku výše. Stačí si uvědomit, že můžeme použít osovou souměrnost. To znamená, že vzdálenost obrazu bodu od zrcadla je vždy stejná jako vzdálenost jeho vzoru.
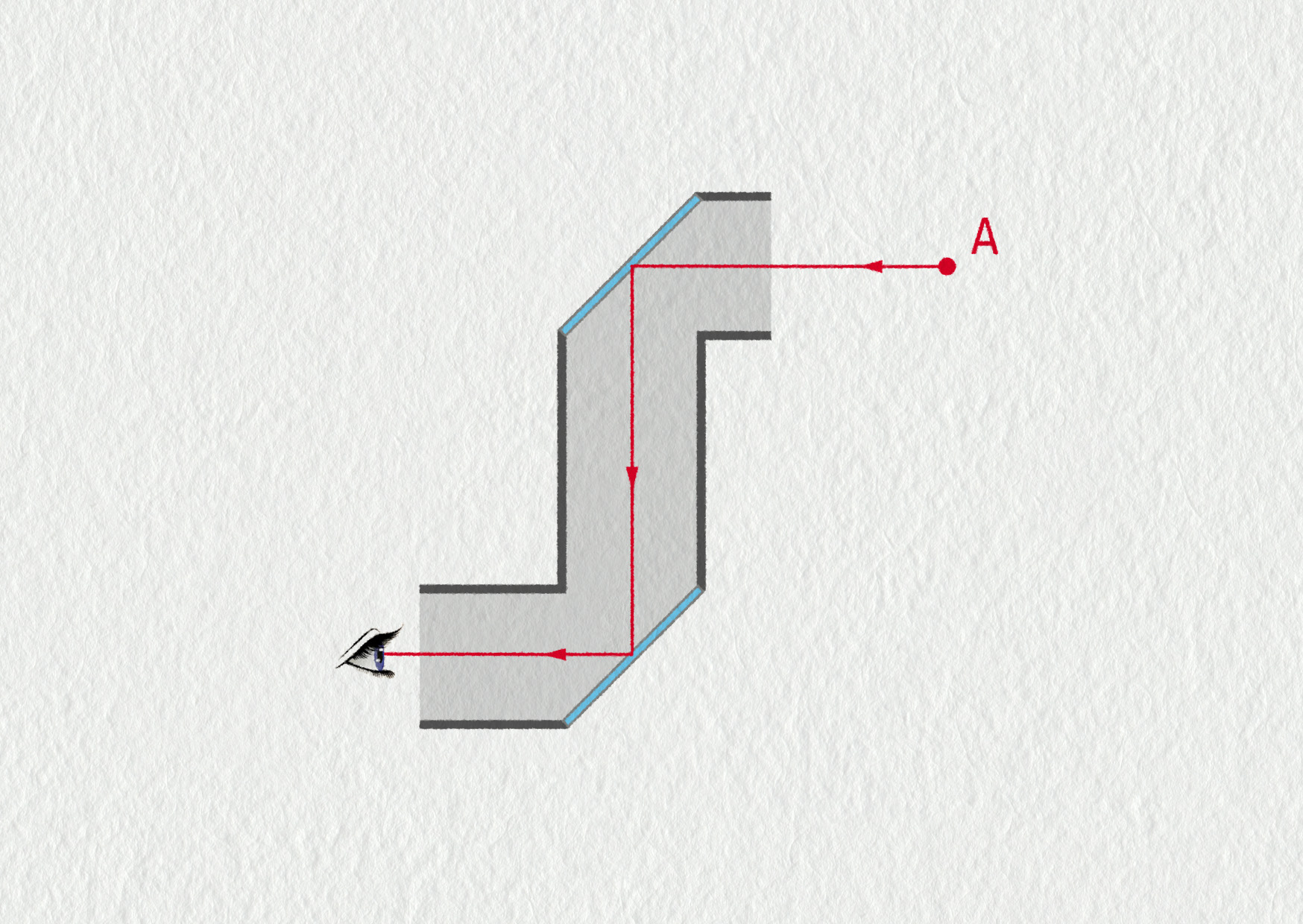
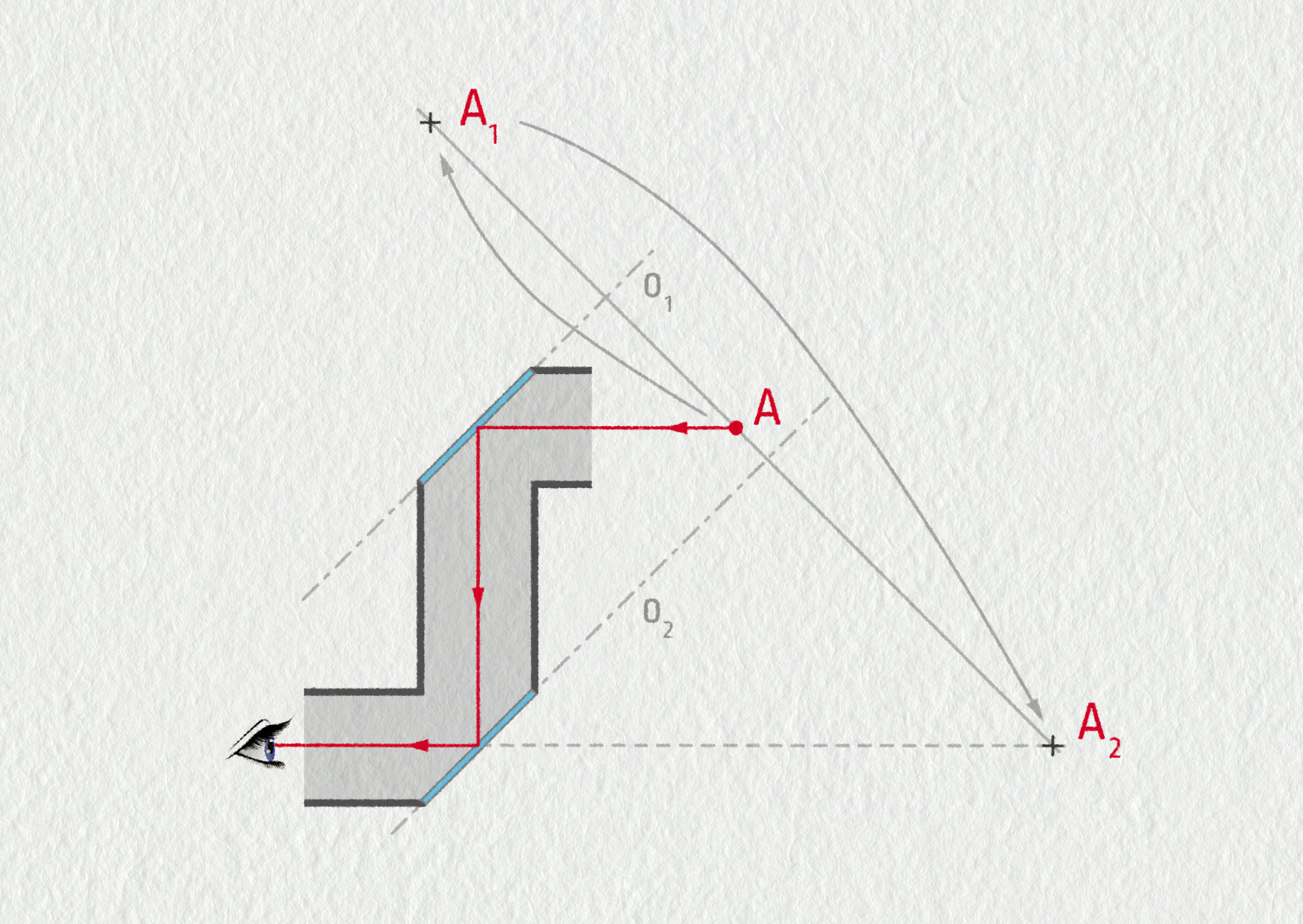
Na obrázku je znázorněn princip periskopu, který umožňuje „vidět za roh“. Periskop je tvořen dvěma rovnoběžnými zrcadly, která jsou umístěna pod úhlem 45° v rozích trubice. Světlo z bodu A se pak dostane do oka pozorovatele vyznačeným způsobem. Kde uvidí pozorovatel bod A? Jinými slovy, kde vznikne neskutečný obraz bodu A?
Zdroj
Nejprve velmi jednoduchá odpověď: bod A uvidíme v tom směru, odkud přichází paprsky do oka, tedy vpravo od něj. Pro určení přesné polohy pozorovaného bodu je nutné najít (neskutečný) obrazu bodu A. To můžeme udělat pomocí dvou osových souměrností, jak je naznačeno na obrázku 2.36. Výsledek je v souladu s naši prvním odhadem.
Zdroj
Pro upřesnění je třeba dodat, že osová souměrnost je zobrazení v rovině. Ve skutečnosti však zobrazení probíhá v prostoru, proto se nejedná o osovou souměrnost, ale souměrnost podle roviny zrcadla. Body se zobrazují na kolmicích k rovině zrcadla ve stejné vzdálenosti. Hezky to ilustruje následující obrázek 2.37. Na osové souměrnosti či souměrnosti podle roviny je zajímavé, že vzor a obraz jsou jen nepřímo shodné. Jednoduše řečeno, mají vyměněnou levou a pravou stranu.

Zdroj
Čočky
Primitivní skleněné čočky byly známé již ve starém Řecku a Římě. Bylo možné pomocí nich například zapálit oheň, případně se používaly jako „zvětšovací skla“. K výrobě kvalitních čoček však potřebujeme vhodný druh skla a přesnou techniku jeho broušení. Proto se první brýle objevily až koncem 12. století v severní Itálii a první dalekohledy pak začátkem 17. století v Nizozemí. Také příroda dokázala pomocí evoluce vyvinout čočku jako součást oka obratlovců či chobotnic.
Čočky používáme především k optickému zobrazování. Zobrazení čočkou je možné díky tomu, že čočka mění směr chodu paprsků přesně určeným způsobem. Světlo se láme na rozhraní čočky a okolního prostředí. Konkrétně pak rozlišujeme dva druhy čoček – spojky a rozptylky.
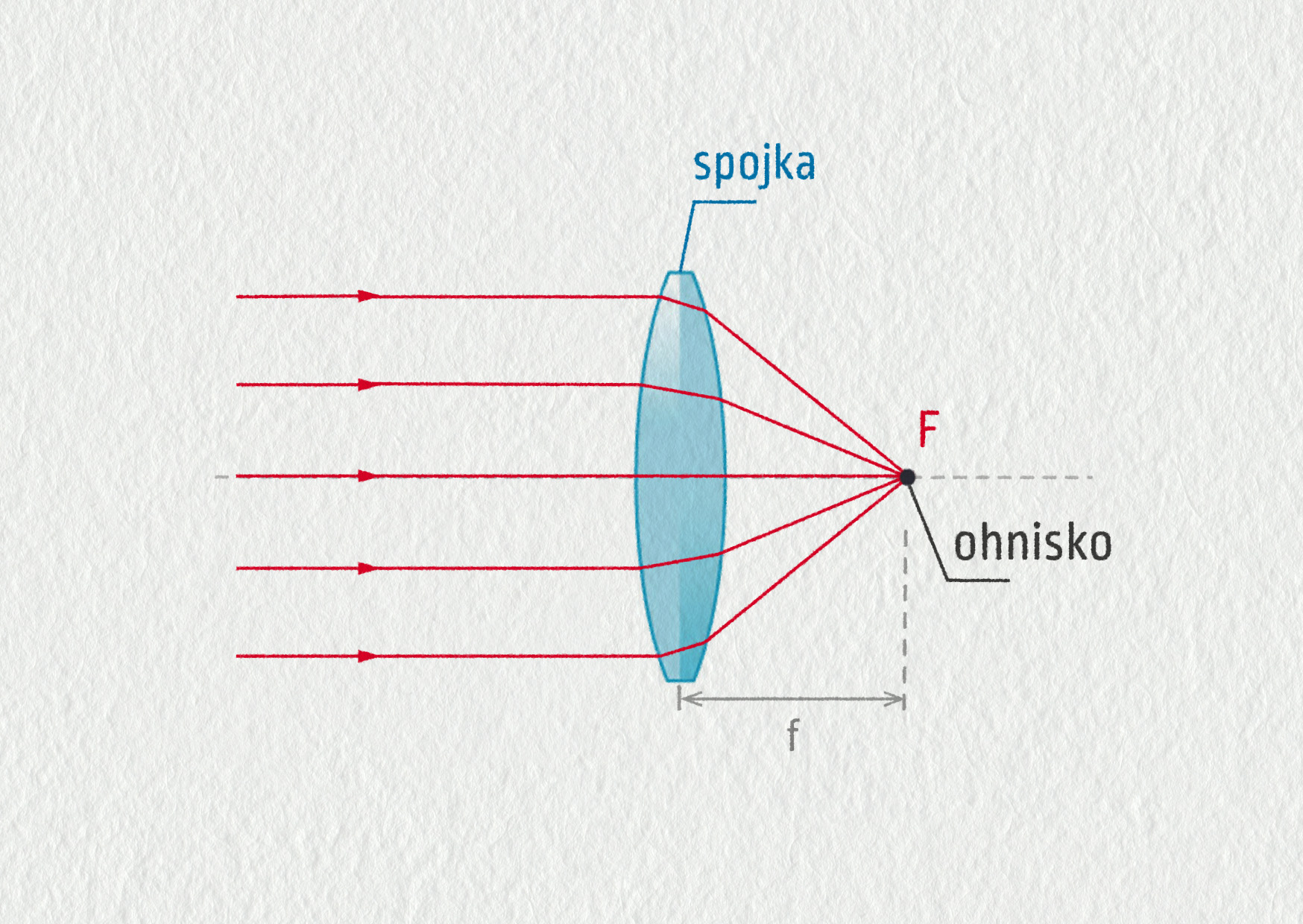
Spojná čočka (spojka) láme světlo tak, že mění rovnoběžný svazek paprsků na svazek sbíhavý. Bod, kde se původně rovnoběžné paprsky protínají, nazýváme ohnisko (F). Vzdálenost ohniska od čočky se nazývá ohnisková délka (\(f\)).
Zdroj
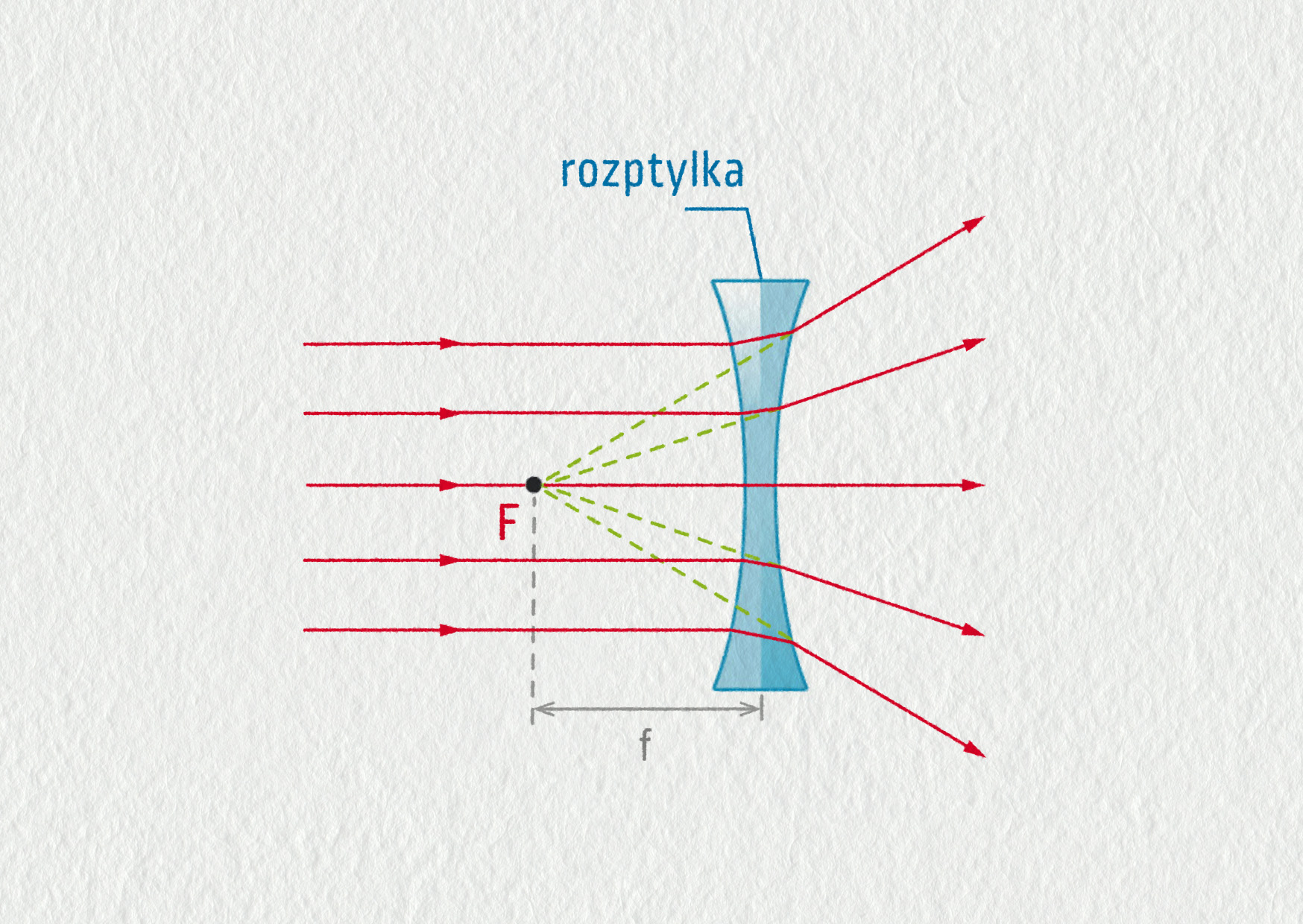
Rozptylná čočka (rozptylka) láme světlo tak, že mění původní rovnoběžný svazek paprsků na svazek rozbíhavý. Bod, ze kterého rozbíhavý svazek zdánlivě vychází, se nazývá ohnisko. U rozptylky leží ohnisko na stejné straně, ze které přichází světlo.
Zdroj
Parametrem, který určuje „sílu“ čočky, je její ohnisková délka \(f\). Silnější čočka láme světlo víc a bude mít ohnisko blíže, její ohnisková délka bude kratší. Podle dohody se dále rozlišuje spojka a rozptylka podle znaménka. Spojky mají ohniskovou délku kladnou, rozptylky zápornou. V praxi se síla čočky často popisuje také pomocí optické mohutnosti. Optická mohutnost je definována jako převrácená hodnota ohniskové délky.
Optická mohutnost čočky:
\(\varphi = 1/f\)
\(f\) – ohnisková délka čočky
Jednotkou optické mohutnosti je m−1, ale v optice je zvykem tuto jednotku nazývat dioptrie (značka D). „Sílu“ čočky tak můžeme popsat dvěma způsoby. Například spojka s ohniskovou délkou 0,5 m má optickou mohutnost 2 D. Silnější spojka o kratší ohniskové délce 0,1 m bude mít větší optickou mohutnost 10 D.
Optická mohutnost se může jevit jako zbytečná veličina; pro popis síly čočky si vystačíme s ohniskovou délkou. Je tu však jedna praktická výhoda. Pokud umístíme čočky těsně k sobě, pak se celková optická mohutnost rovná součtu optických mohutností jednotlivých čoček. Řečeno matematicky: \(\varphi=\varphi_1+\varphi_2\).
Pojďme se nyní zaměřit na problém, jak vyrobit čočku, aby měla výše uvedené vlastnosti. Většinou se čočky brousí ze skla, ale mohou být i plastové. Volbou materiálu určíme index lomu. Jaký musí mít čočka tvar? Nejjednodušší možností je kulová čočka ohraničená dvěma kulovými plochami, které jsou charakterizované svými poloměry. Na obrázku 23.41 vidíme tři různé čočky (přesněji jejich 2D provedení) na optické tabuli. Všimněte si, že čočky na obrázku mají jednu stranu rovnou. Rovinu můžeme chápat jako kulovou plochu o nekonečném poloměru. Přesný vztah pro ohniskovou délku kulové čočky najdete v poznámce.

Zdroj
Ohnisková vzdálenost je základní parametr čočky, který závisí obecně na poloměrech křivosti čočky \(r_1\) a \(r_2\), tloušťce čočky \(d\) a na jejím indexu lomu \(n\) podle následujícího vztahu (za předpokladu, že okolí má index lomu roven 1):
\[ \frac1f = (n-1)\left(\frac1{r_1}-\frac1{r_2}\right) + \frac{d(n-1)^2}{nr_1r_2} \]Vidíme, že uvedený vztah je poměrně komplikovaný, ale dá se pomocí základní aproximace a vhodně zvolené čočky výrazně zjednodušit. Pokud využijeme aproximace tenké čočky, u které lze tloušťku čočky zanedbat (\(d=0\ \mathrm{m}\)), tak se vynuluje poslední člen v předcházející rovnici. Dostaneme vztah
\[ \frac1f = (n-1)\left(\frac1{r_1}-\frac1{r_2}\right) \]Pokud navíc zvolíme ploskovypuklou čočku (jedna strana je rovná), která má jeden z poloměrů křivosti roven nekonečnu, tak dojde opět k dalšímu zjednoduší rovnice:
\[ \frac1f = (n-1)\frac1{r_1} \quad\Rightarrow\quad f = \frac{r_1}{n-1} \]Tento zjednodušený vztah dává do přímé souvislosti dva základní parametry čočky (index lomu \(n\) a poloměr křivosti \(r_1\)) s ohniskovou vzdáleností čočky \(f\).
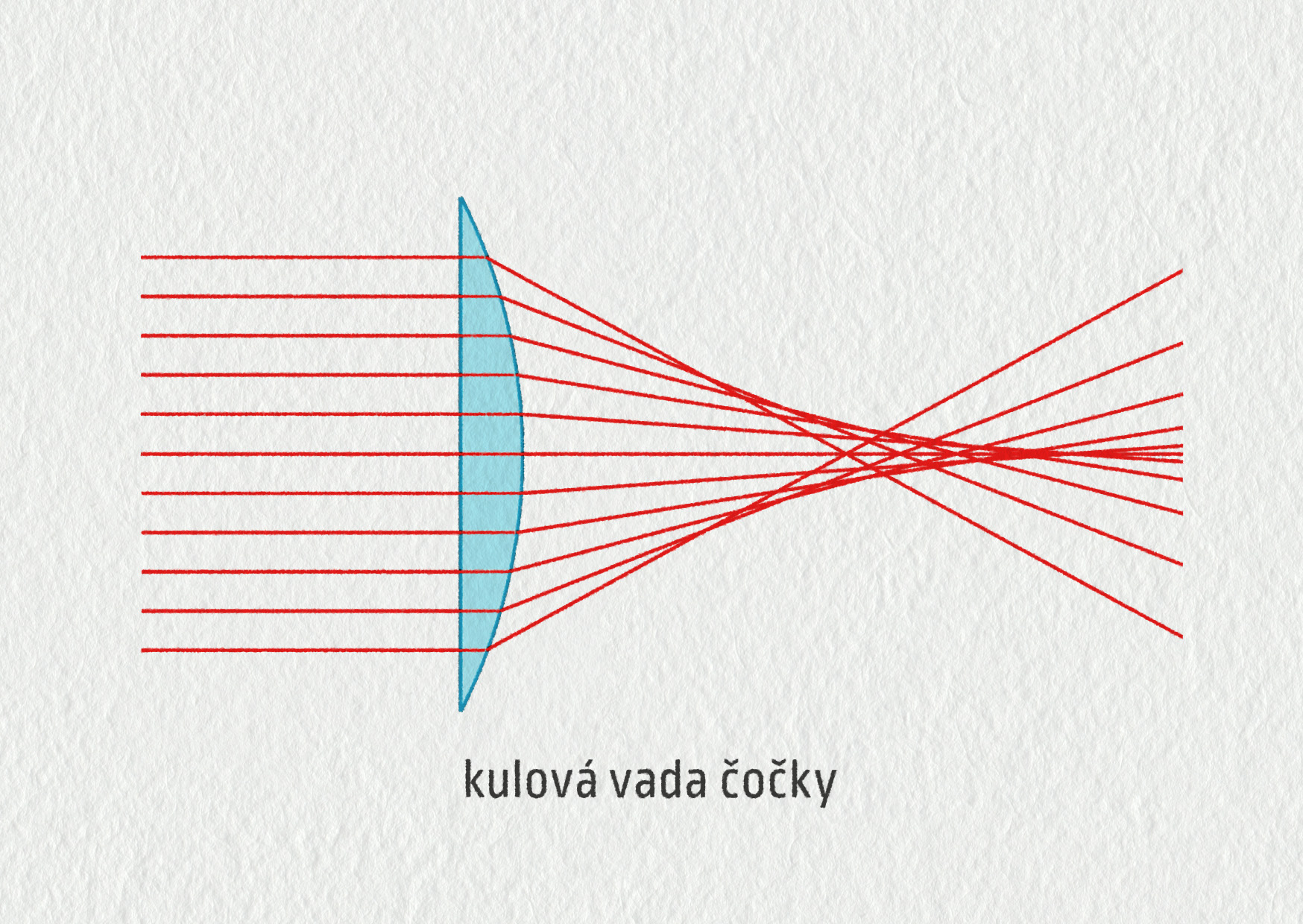
Kulová čočka ovšem neláme světlo zcela přesně. Při zobrazování pak vznikají nejrůznější vady. Pro konstrukci kvalitních optických přístrojů se proto používají čočky složitějšího tvaru, případně také kombinace více čoček a kombinace různých materiálů. Dvě nejdůležitější optické vady shrnují následující obrázky 23.42 a 23.43.
Zdroj
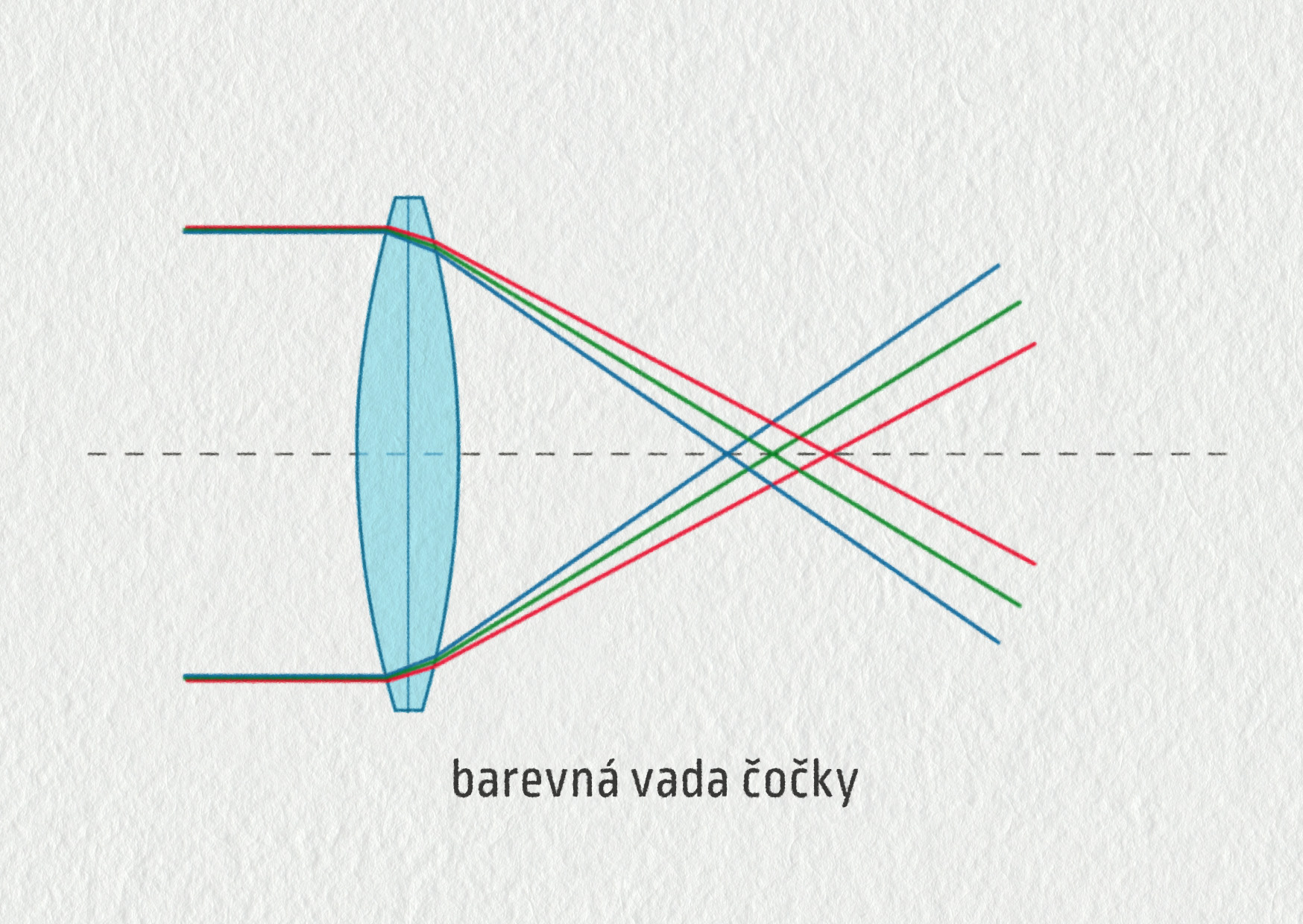
Zdroj

Zdroj
Geometrická konstrukce zobrazení
V tomto odstavci se seznámíme s jednoduchým postupem, jak můžeme pomocí geometrie konstruovat obrazy předmětů, které vytváří čočky. Pro tento účel budeme používat následující pojmy. Jejich znázornění můžete sledovat na obrázku 23.45.
Optická osa je přímka procházející středem spojky, která je na ni kolmá.
Tenká čočka je čočka, jejíž tloušťku je možné zanedbat. Proto ji budeme znázorňovat jako úsečku.
Ohnisko spojky je bod, kde se sbíhají původně rovnoběžné paprsky. Ohnisko rozptylky je bod, ze kterého zdánlivě vycházejí původně rozbíhavé paprsky. Každá čočka má dvě ohniska ležící souměrně na obou stranách.
Význačné paprsky jsou vybrané paprsky, které používáme ke konstrukci obrazu.
1) Paprsek procházející středem čočky po průchodu čočkou nemění svůj směr.
2a) Spojka: paprsek rovnoběžný s optickou osou se po průchodu čočkou láme do ohniska.
2b) Rozptylka: paprsek rovnoběžný s optickou osou se láme tak, že zdánlivě vychází z ohniska.
3a) Spojka: paprsek procházející ohniskem se láme na rovnoběžný s optickou osou.
3b) Rozptylka: paprsek směřující do ohniska na druhé straně čočky se láme na rovnoběžný s optickou osou.
Ke konstrukci obrazu stačí použít k získání průsečíku pouze dva význačné paprsky. Třetí paprsek může posloužit jako kontrolní.
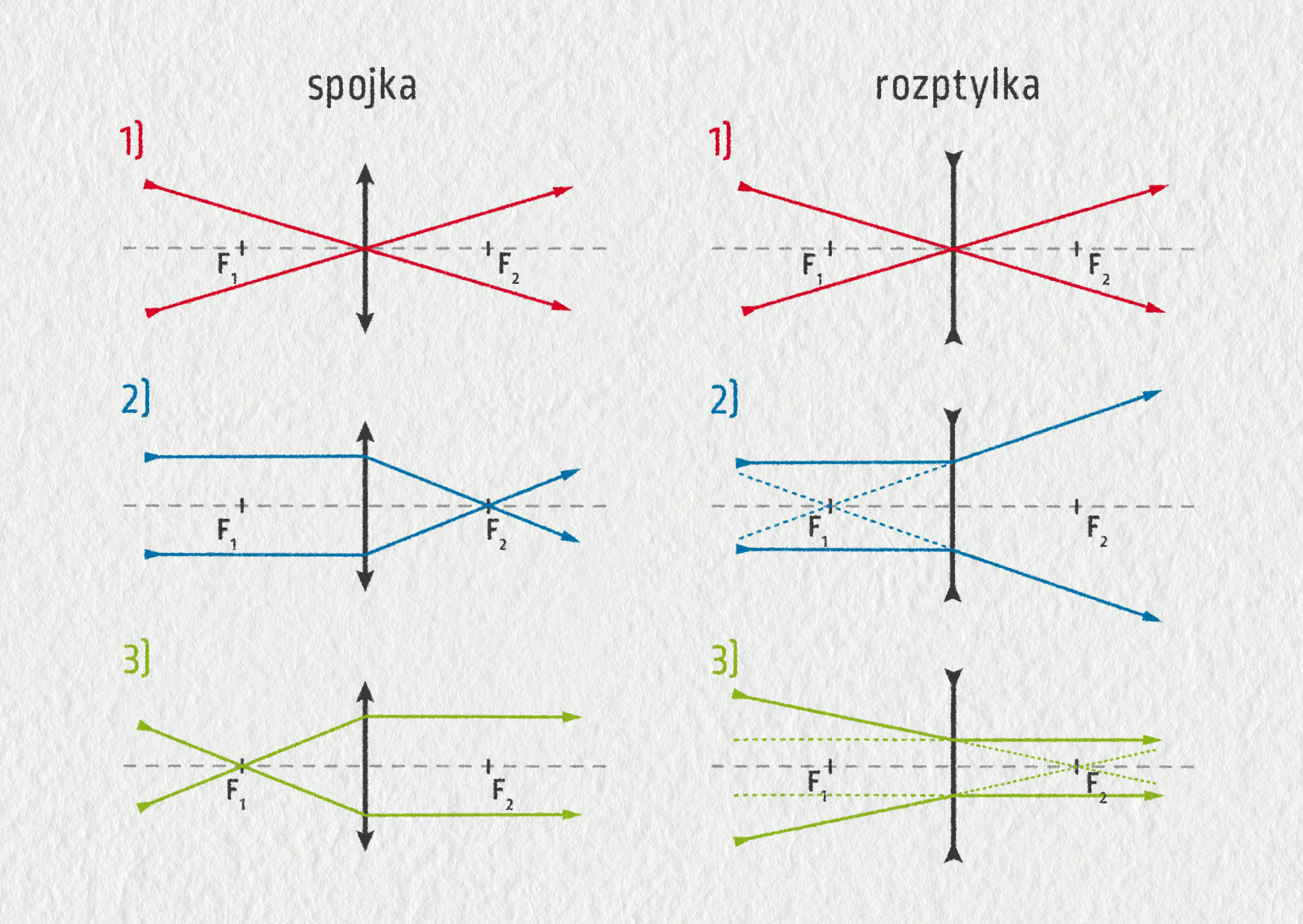
Zdroj
Většinou chceme sestrojit obraz konkrétního předmětu. K tomu nám stačí vybrat si libovolný bod tohoto předmětu, který neleží na optické ose, a provést jeho zobrazení pomocí význačných paprsků. Předmět pak znázorňujeme schematicky pomocí šipky. Na ukázku jsou na následujícím obrázku provedeny dvě konstrukce obrazu pro konkrétní spojku a rozptylku.
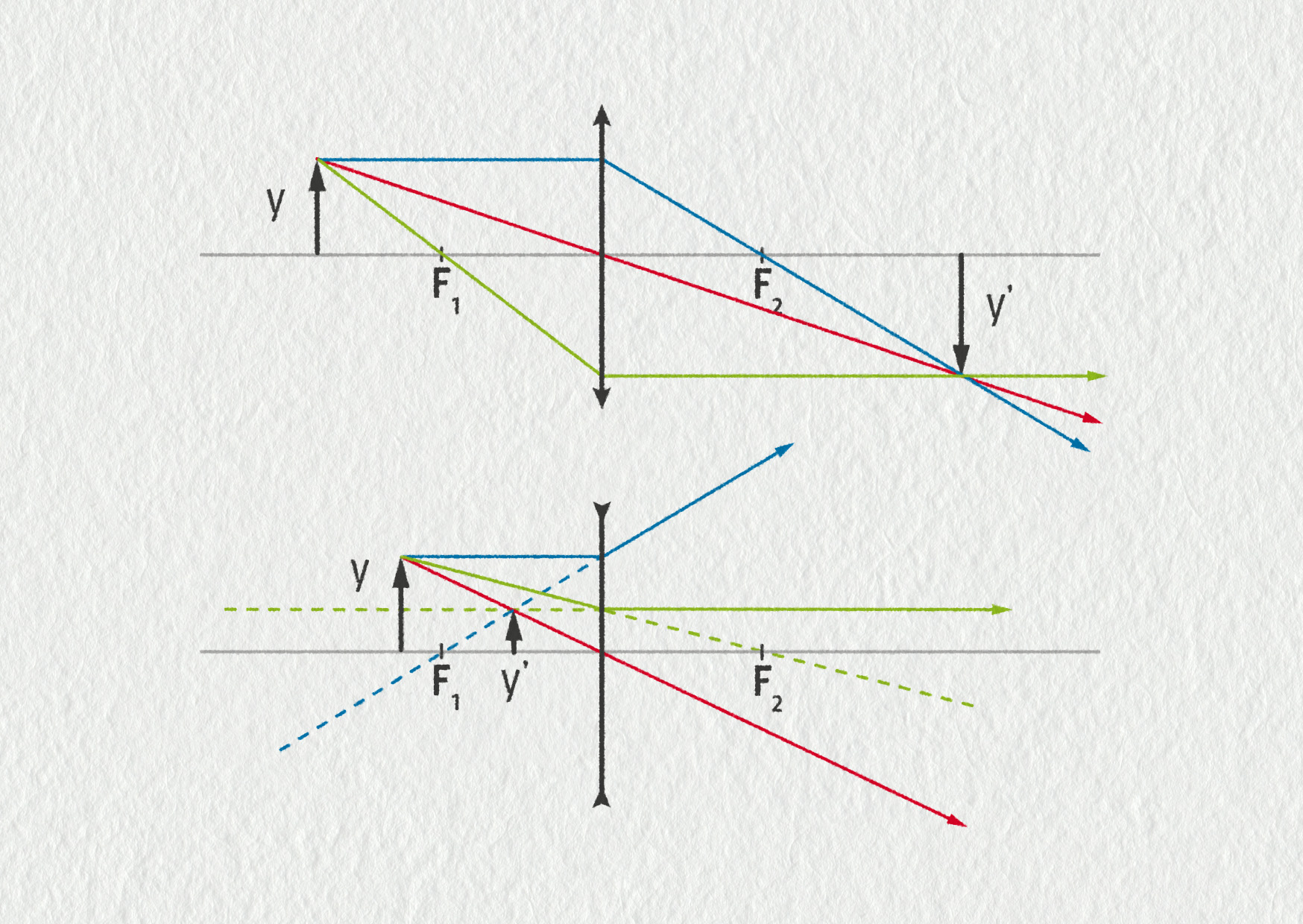
Zdroj
Provedené zobrazení nám umožňuje z konstrukce „vyčíst“ důležité vlastnosti obrazu.
- Je obraz skutečný nebo neskutečný? Skutečný obraz vytváří sbíhavé paprsky (první konstrukce), zatímco neskutečný obraz se nachází ve zdánlivém zdroji rozbíhavých paprsků (druhá konstrukce).
- Je obraz zvětšený nebo zmenšený? Zvětšení určíme snadno pomocí poměru velikostí šipek. V první konstrukci jde o zvětšený obraz a naopak v druhé o zmenšený.
- Je obraz přímý nebo převrácený? Jsou-li předmět i obraz na stejné straně optické osy a šipky míří stejným směrem, jde o přímý obraz (druhá konstrukce). V opačném případě se jedná o převrácený obraz (první konstrukce).
Vlastnosti obrazu závisí na druhu čočky, ale také na vzdálenosti předmětu od čočky. Abyste nemuseli dlouho rýsovat, doporučujeme rozpohybovat si zobrazení pomocí geogebry. Na základě této simulace pak můžete snadno vyřešit následující příklad.
Spojka v geogebře: https://www.geogebra.org/m/yspcx4b8
Rozptylka v geogebře: https://www.geogebra.org/m/qm23pjzg
Doplňte druhý sloupec tabulky pro typické vzdálenosti předmětu od spojky.
| předmětová vzdálenost \(a\) | vlastnosti obrazu |
|---|---|
| \(a > 2f\) | |
| \(a = 2f\) | |
| \(2f > a > f\) | |
| \(a = f\) | |
| \(f > a > 0\) |
V případě rozptylky je situace mnohem jednodušší. Tabulka má jediný řádek.
| předmětová vzdálenost \(a\) | vlastnosti obrazu |
|---|---|
| \(a > 0\) |
Spojka
| předmětová vzdálenost \(a\) | vlastnosti obrazu |
|---|---|
| \(a > 2f\) | převrácený, skutečný a zmenšený |
| \(a = 2f\) | převrácený, skutečný a stejně velký |
| \(2f > a > f\) | převrácený, skutečný a zvětšený |
| \(a = f\) | přímý obraz v nekonečnu |
| \(f > a > 0\) | přímý, neskutečný a zvětšený |
Rozptylka
| předmětová vzdálenost \(a\) | vlastnosti obrazu |
|---|---|
| \(a > 0\) | přímý, neskutečný a zmenšený |
Chcete-li si rýsování obrazů trochu procvičit pomocí tužky a pravítka, můžete si stáhnout tento pracovní list.
Zobrazovací rovnice
Už víme, jak najít obraz geometrickou konstrukcí a jaké může mít vlastnosti. Existuje ale ještě jeden elegantnější způsob, jak popsat zobrazení, a to výpočtem pomocí zobrazovací rovnice čočky. Ta popisuje souvislost mezi ohniskovou délkou \(f\), vzdáleností předmětu \(a\) a vzdáleností obrazu \(a'\). Kromě toho můžeme přesně vypočítat také zvětšení čočky \(Z\), a to jako podíl velikosti obrazu \(y'\) a velikosti předmětu \(y\). Veličiny jsou přehledně vyznačeny na obrázku 23.47.
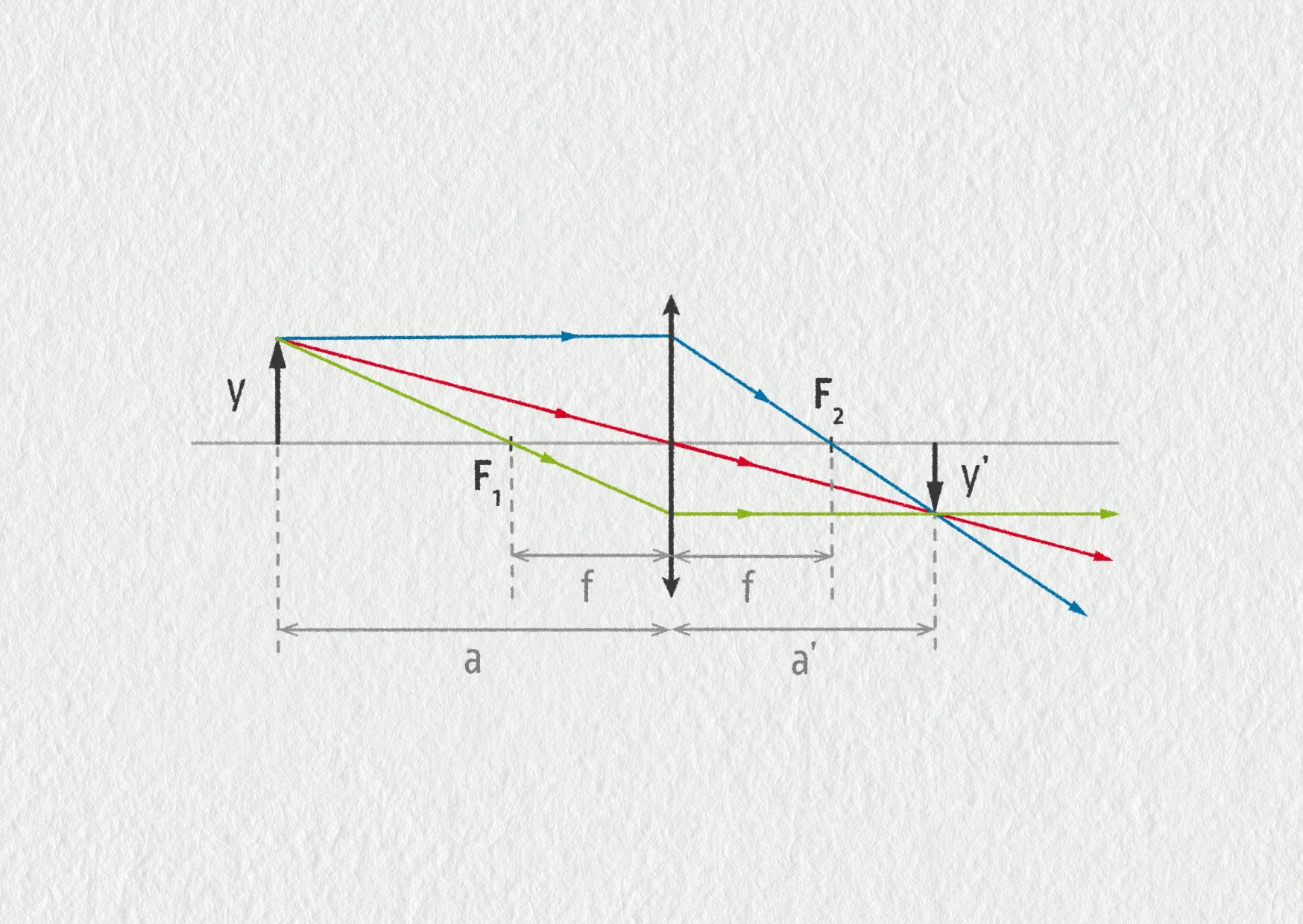
Zdroj
Zobrazovací rovnice vyjadřuje vztah mezi veličinami \(a\), \(a'\) a \(f\):
Zobrazovací rovnice čočky:
\[ \frac1a + \frac1{a'} = \frac1f \]Zvětšení:
\[ Z = \frac{y'}y = -\frac{a'}a \]\(a\) – předmětová vzdálenost
\(a'\) – obrazová vzdálenost
\(y\) – poloha předmětu
\(y'\) – poloha obrazu
\(f\) – ohnisková délka čočky
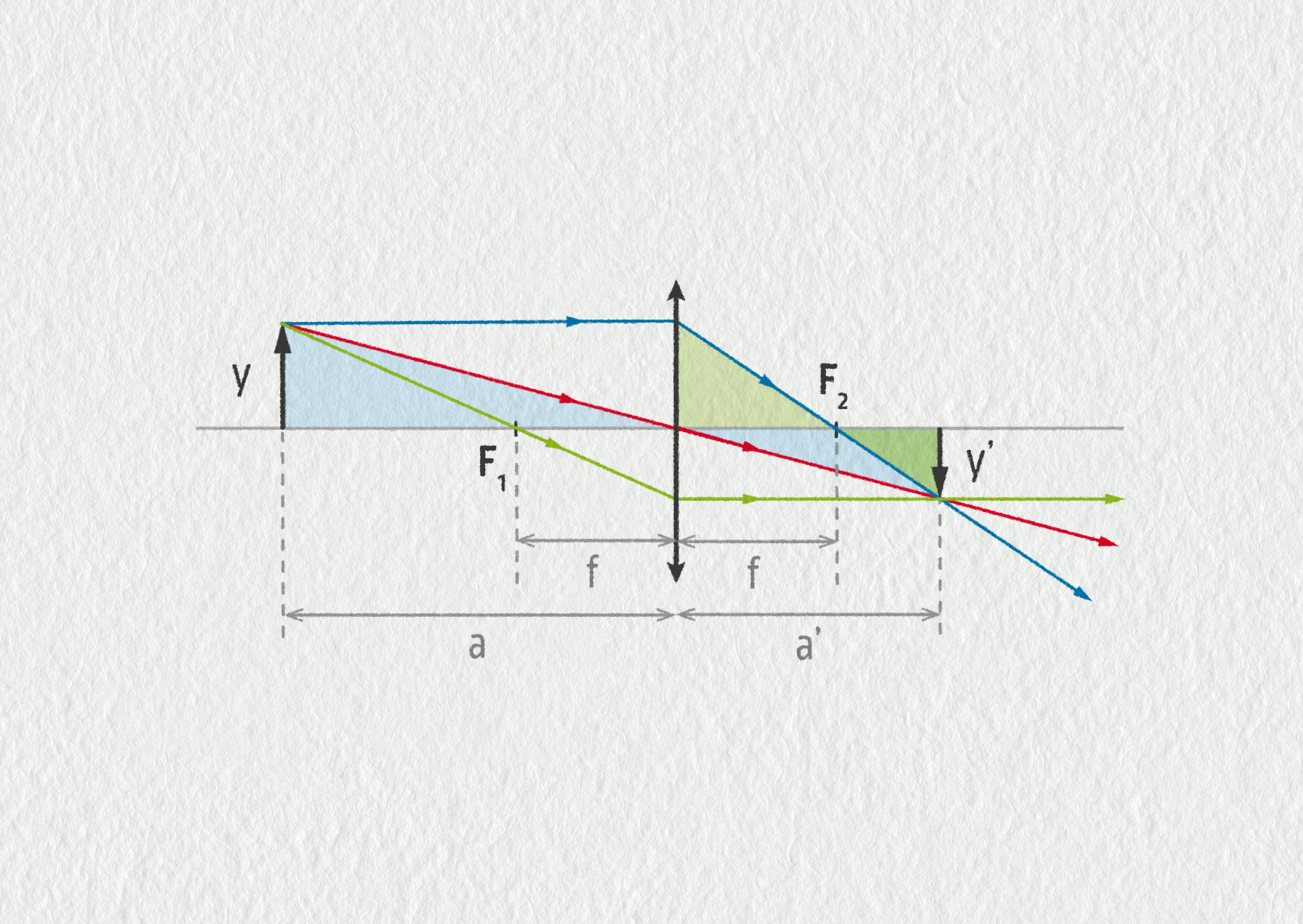
Zobrazovací rovnici je možné elegantně odvodit pomocí podobných trojúhelníků, což je provedeno v poznámce.
V obrázku jsou vybarvené dvojice podobných trojúhelníků.
Zdroj
Z obrázku plyne, že \(a'/a=y'/y\) (modré trojúhelníky) a \(y'/y=(a'-f)/f\) (zelené trojúhelníky).
Porovnáním obou rovnic dostaneme
\[ \frac{a'}a=\frac{a'-f}f\;. \]Odtud pak násobením af získáme
\[ fa' = aa' - af \quad\Rightarrow\quad fa' + fa = aa'\;. \]Poslední rovnici vydělíme \(aa'f\) a dostaneme
\[ \frac1a + \frac1{a'} = \frac1f \]Abychom mohli pomocí zobrazovací rovnice řešit všechny úlohy, je potřeba dodržovat určitý systém ve znaménkách použitých veličin:
| \(f\) | kladné | spojka |
| záporné | rozptylka | |
| \(a\) | kladné | předmět je před čočkou |
| záporné | — | |
| \(a'\) | kladné | obraz je za čočkou (skutečný) |
| záporné | obraz je před čočkou (neskutečný) | |
| \(Z\) | kladné | obraz je přímý |
| záporné | obraz je převrácený |
Nyní je již používání zobrazovací rovnice velmi snadné. Je to elegantnější a rychlejší metoda než geometrická konstrukce.
Zobrazujeme spojkou o ohniskové délce 2 cm. Předmět se nachází 80 cm od čočky. Určete polohu a vlastnosti obrazu.
Ze zadání vyplývá, že \(f=2\ \mathrm{cm}\) a \(a=80\ \mathrm{cm}\). Ze zobrazovací rovnice nejprve vyjádříme neznámou \(a'\):
\[\begin{aligned} \frac1a + \frac1{a'} &= \frac1f\\ \frac1{a'} &= \frac1f - \frac1a\\ a' &= \frac{af}{a-f}\\ \end{aligned}\]Nyní můžeme dosadit hodnoty v cm a dostáváme
\[ a' = \frac{80\cdot2}{80-2}\ \mathrm{cm} = 2{,}05\ \mathrm{cm}\;. \]Pro zvětšení platí:
\[ Z = -a'/a = -2{,}05/80 = -0{,}025\;. \]Závěr: Vznikne skutečný, převrácený, zmenšený obraz ve vzdálenosti 2,05 cm od čočky. Obraz bude zmenšený na 0,025 násobek své původní velikosti. Přesná konstrukce této úlohy není možná, protože poměr velikosti předmětu a obrazu je příliš velký. Situace zhruba odpovídá zobrazení v lidském oku.
Zobrazujeme spojkou o ohniskové délce 40 mm. Předmět se nachází 36 mm od čočky. Určete polohu a vlastnosti obrazu.
Vycházíme z obecného řešení předchozího příkladu.
\[ a' = \frac{af}{a-f} = \frac{36\cdot40}{36-40}\ \mathrm{mm} = -360\ \mathrm{mm}\;. \] \[ Z = -a'/a = 360/40 = 9\;. \]Závěr: Pozorujeme neskutečný, přímý, zvětšený obraz ve vzdálenosti 360 mm před čočkou. Obraz bude zvětšený na devítinásobek své původní velikosti. Situace odpovídá zobrazení lupou, kterou ještě podrobněji probereme později.
Zrcadla
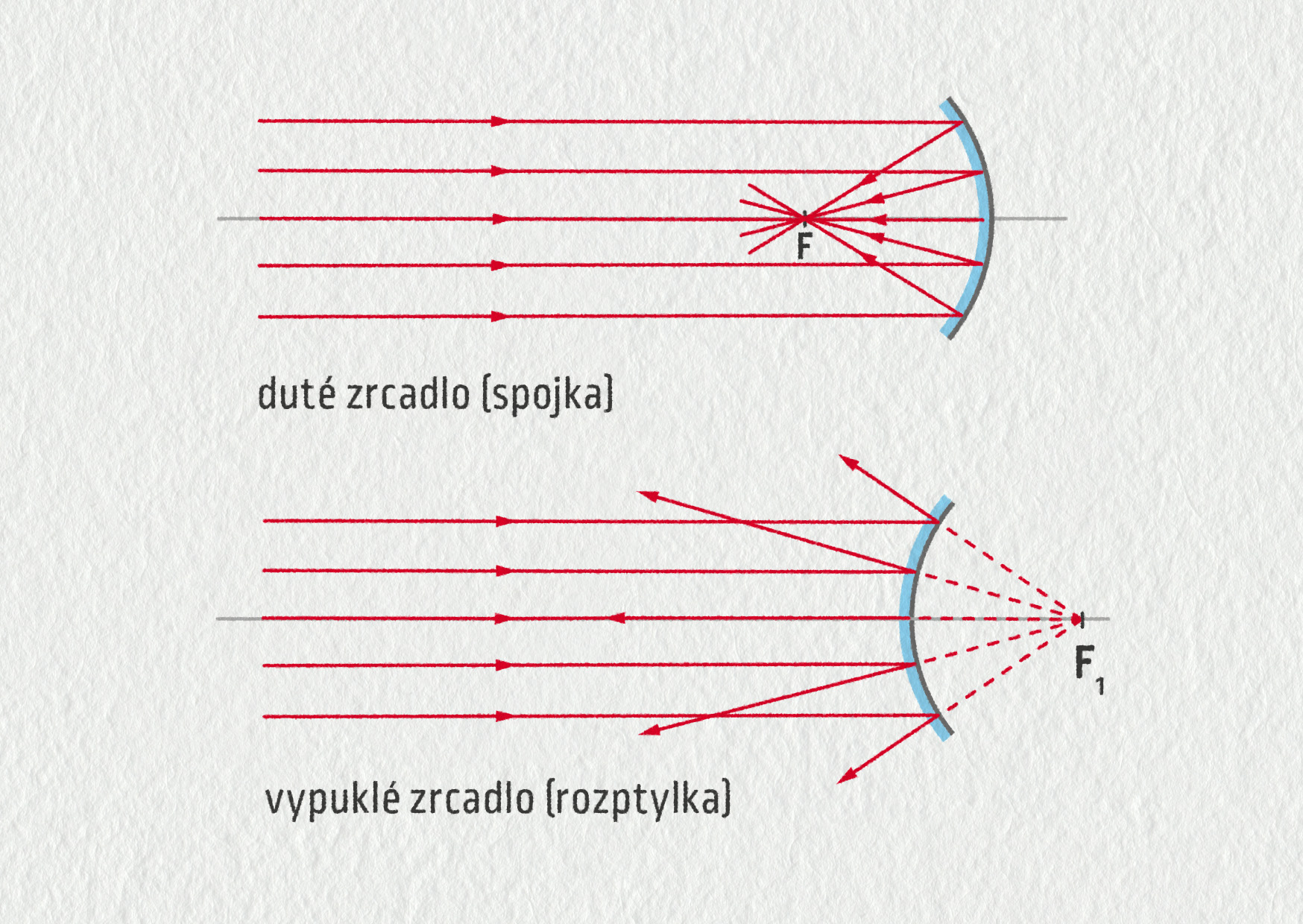
Kromě čoček můžeme ke zobrazování používat také zrcadla. Kromě rovinného zrcadla se nabízí také zrcadla zakřivená. Spojka se chová podobně jako duté zrcadlo, rozptylka pak jako vypuklé zrcadlo. Vše je přehledně znázorněno na obrázku 23.49.
Zdroj
Podobně jako u čoček, je nejjednodušší možností zrcadlo tvořené částí kulového povrchu. To je charakterizované poloměrem křivosti \(r\). Pro jeho ohniskovou délku pak platí:
\[ f = r/2\;. \]Zrcadlo, které netrpí kulovou vadou, se nazývá parabolické a má tvar rotačního paraboloidu. Navíc u zrcadel není problém s disperzí způsobující barevnou vadu čoček. Proto se zrcadla používají třeba v astronomických dalekohledech. Na druhou stranu má zrcadlo jednu podstatnou nevýhodu. Skutečný obraz vzniká na stejné straně jako předmět, proto se zrcadla nehodí pro běžná zobrazovací zařízení, jako jsou fotoaparáty.
Oba nástroje pro hledání polohy obrazu fungují také pro zrcadla. Při konstrukci pomocí význačných paprsků pouze místo lomených paprsků rýsujeme paprsky odražené. V případě zobrazovací rovnice se pouze prohodí význam znaménka polohy obrazu. Kladné \(a'\) znamená obraz před zrcadlem (skutečný) a záporné \(a'\) znamená obraz za zrcadlem (neskutečný).
Duté zrcadlo se používá v reflektorech k vytváření málo rozbíhavých svazků světla. Najdete je například v dálkových světlech u aut nebo jako osvětlení na koncertech. V jaké pozici vůči zrcadlu se musí nacházet zdroj světla, aby vznikl rovnoběžný svazek paprsků? Popsanou situaci načrtněte.

Zdroj
Zdroj světla se musí nacházet v ohnisku dutého zrcadla (nejlépe parabolického).
Kosmetické zrcadlo je duté zrcadlo, ve kterém se můžete vidět „zvětšeně“. Uvažujme kosmetické zrcadlo o ohniskové délce 30 cm.
- V jaké vzdálenosti musí být obličej člověka, aby mohl v zrcadle pozorovat svůj neskutečný, zvětšený a přímý obraz?
- Vypočítejte, jak se zobrazí předmět, který je ve vzdálenosti 20 cm od zrcadla.
a) Obličej člověka se musí nacházet mezi zrcadlem a ohniskem, tedy maximálně 30 cm od zrcadla.
b) Duté zrcadlo se chová stejně jako spojka, použijeme zobrazovací rovnici.
\[\begin{aligned} \frac1a + \frac1{a'} &= \frac1f\\ \frac1{a'} &= \frac1f - \frac1a\\ a' &= \frac{af}{a-f}\\ \end{aligned}\]Nyní můžeme dosadit hodnoty v cm a dostáváme
\[ a' = \frac{20\cdot30}{20-30}\ \mathrm{cm} = -60\ \mathrm{cm}\;. \]Pro zvětšení platí:
\[ Z = -a'/a = -(-60)/20 = 3\;. \]Čočky a zrcadla

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

