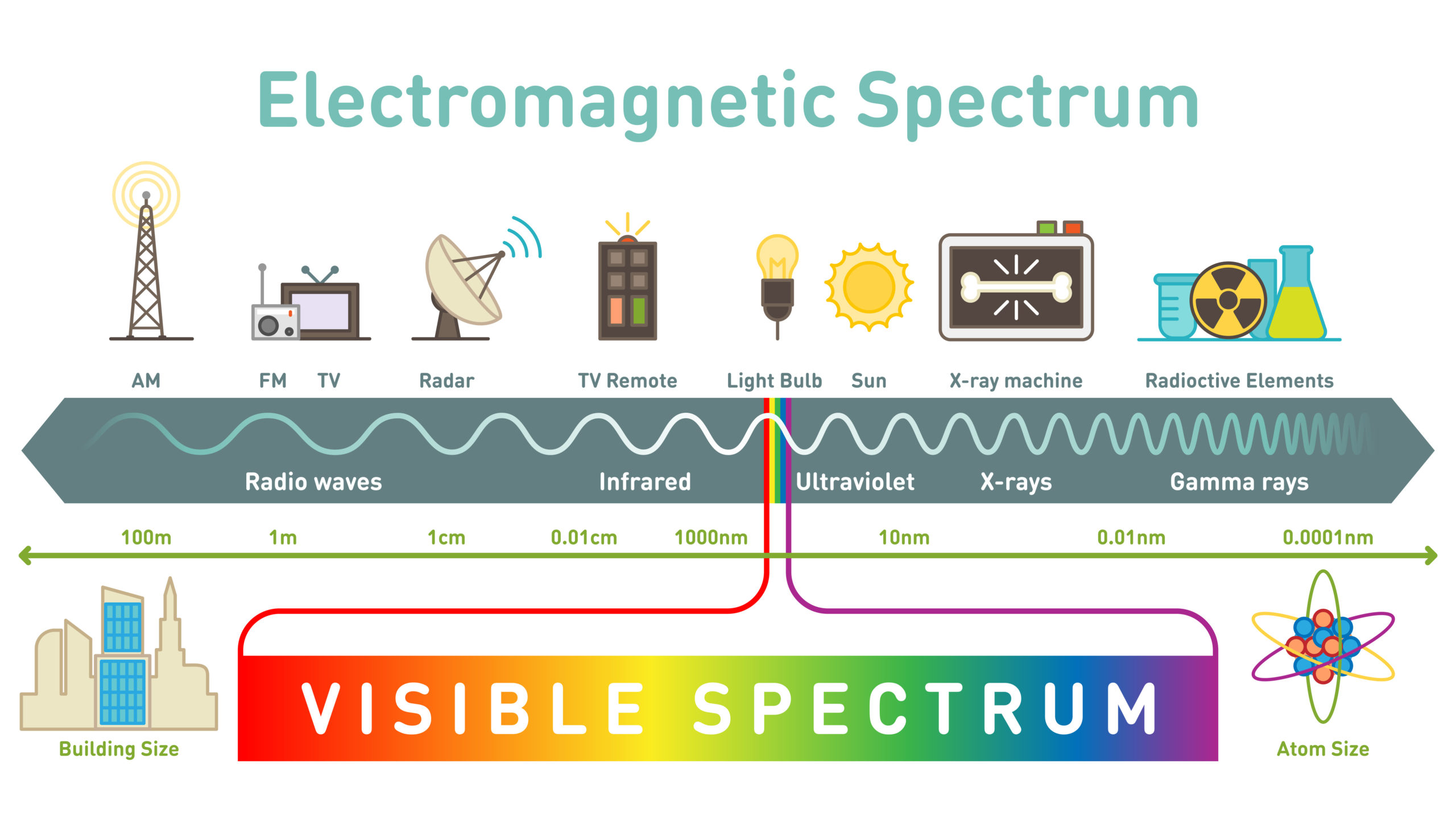
V minulých kapitolách jsme se dozvěděli, že světlo je určitý druh elektromagnetické vlny, který se může projevit také jako svazek částic – fotonů. V této kapitole se pokusíme naše znalosti o světle rozšířit na další druhy elektromagnetických vlnění. Světlo je část elektromagnetického spektra, kterou dokážeme vnímat okem. Přísluší mu vlnové délky od 380 nm do 780 nm. Jaké druhy elektromagnetických vlnění leží vně tohoto intervalu? Jaké mají vlastnosti?
Zdroj
Na předcházejícím obrázku si můžeme prohlédnout, jaké další druhy elektromagnetického vlnění existují. Dejme ovšem pozor na měřítko vodorovné osy. Je na něm znázorněna vlnová délka. Není však vynesena lineárně, ale v logaritmickém měřítku. Pokud bychom tato záření seřadili na ose lineárně a viditelné záření (světlo) by odpovídalo šířce jedné oktávy klavíru, celá délka našeho nástroje by sahala velmi daleko, až do vzdálenosti odpovídající 1 astronomické jednotce (150 ⋅ 106 km). Tak obrovská je „klaviatura“ našeho nástroje, který se v této kapitole pokusíme popsat.
| Druh | Rozsah vlnových délek \(\lambda\) | Zdroj | Vlastnosti | Využití v astronomii | Další využití |
|---|---|---|---|---|---|
| radiové | 30 km až 1 m | elektromagnetický oscilátor | vlnové vlastnosti, šíří se dobře na velké vzdálenosti | výtrysky černých děr, molekulární a prachová mračna | rozhlasové vysílání, námořní a letecká komunikace |
| mikrovlnné | 1 m až 0,3 mm | elektromagnetický oscilátor, magnetron | vlnové vlastnosti, optimální pro přenos dat | reliktní záření, plyn a prach v galaxiích, rodící se hvězdy | televizní vysílání, GPS komunikace, mikrovlnná trouba, sušení dřeva, wi-fi, bluetooth, radar |
| infračervené | 0,3 mm až 780 nm | zahřátá tělesa (teploty v rozsahu přibližně −240 °C až 17 700 °C) | přenos tepla, málo pohlcováno vodou, dobře proniká přes zakalené prostředí, částečně pohlcováno zemskou atmosférou | dálkový průzkum Země, výzkum planetárních atmosfér, plynu a prachu v galaxiích, exoplanet, mlhovin, hnědých trpaslíků a červených obrů | bezkontaktní teploměry, dálková ovládání, termovize, rehabilitace |
| viditelné | 780 nm až 380 nm | horké zdroje (hvězdy, plamen, žárovka), přechody elektronlů v atomech (výbojka) nebo v pevných látkách (LED) | vlnový i částicový charakter, jeho studiem se zabývá optika | základní pozorování hvězd | zdroj informací pro člověka, nezbytné při fotosyntéze, zdroj energie až fotovoltaika |
| ultrafialové | 380 nm až 10 nm | horké hvězdy, rtuťová výbojka, elektrický oblouk | vyvolává luminiscenci, pohlcováno obyčejným sklem, ionizační účinky | pozorování mladých hvězd, novy a supernovy, polární záře | sterilizace vody, nástrojů, vytvrzování materiálů, umění, ochrana bankovek a dokladů |
| rentgenové | 10 nm až 1 pm | rentgenka | ionizační účinky, proniká i pevnými látkami | studim sluneční korony, pulsarů akrečních disků černých děr | technické a lékařské zobrazování, léčba zhoubných nádorů |
| gama | méně než 1 pm | rentgenka, rozpad atomových jader | silné ionizační účinky, proniká i pevnými látkami | neutronové hvězdy, černé díry, exploze supernov | radiogeneze, sterilizace, léčba zhoubných nádorů |
Elektromagnetickým vlnám přiřazujeme vlnovou délku \(\lambda\) a frekvenci \(f\), které spolu souvisí známým vztahem \(\lambda=c/f\). Symbol \(c\) označuje rychlost šíření vln (světla) ve vakuu. Má velikost \(c=299\,792\,458\ \mathrm{m/s}\approx3{,}00\cdot10^8\ \mathrm{m/s}\). Základní dělení elektromagnetických vln podle vlnové délky a společných vlastností je uvedeno v tabulce.
Elektromagnetickou vlnu můžeme také popsat podle energie fotonů příslušné frekvence: \(E=hf\), kde \(h=6{,}626\,070\,15\cdot10^{-34}\ \mathrm{J}\cdot\mathrm{s}\) je hodnota Planckovy konstanty a \(f\) frekvence elektromagnetické vlny. Vlnění s vysokou frekvencí (počínaje ultrafialovým vlněním) nazýváme ionizující záření kvůli jeho účinkům na atomy a molekuly. Toto záření přenáší tak velkou energii, že při průchodu látkou a jeho částečné či úplné absorpci dochází k uvolnění elektronů z původně neutrálního atomu a vzniku iontu.
Záření černého tělesa
Všechny látky produkují elektromagnetické záření, které je způsobeno tepelným pohybem (kmitáním) jejich částic. Hovoříme o tepelném záření. Z praxe víme, že při teplotě okolo 500 stupňů Celsia začíná tepelné záření zasahovat i do viditelné oblasti spektra – pozorujeme slabé červené zbarvení. S rostoucí teplotou se intenzita záření zesiluje a barva se posouvá směrem ke žluté.

Zdroj
Koncem 19. století se fyzikové marně pokoušeli vytvořit teoretický model záření těles. Povedlo se to až v roce 1900 Maxovi Planckovi pomocí kvantové hypotézy. Ve svém modelu předpokládal, že energie z tělesa odchází po kvantech, nikoliv spojitě. Bylo to vůbec poprvé, kdy se ve fyzice objevila myšlenka kvantování energie.
Planckův vyzařovací zákon platí pro absolutně černé těleso. To je ideální těleso, které pohlcuje veškeré záření všech vlnových délek, které na něj dopadá. Absolutně černé těleso je současně ideální zářič; ze všech těles o stejné teplotě vysílá největší možné množství zářivé energie. Černé těleso podle Planckova zákona vyzařuje spojité elektromagnetické záření, které závisí pouze na teplotě tělesa. Toto záření vzniká pouze tepelným pohybem částic v tělese. Velmi dobrým příkladem černého tělesa jsou hvězdy. Naopak tělesa s kovovým povrchem se jako černá nechovají – záření se od nich silně odráží.
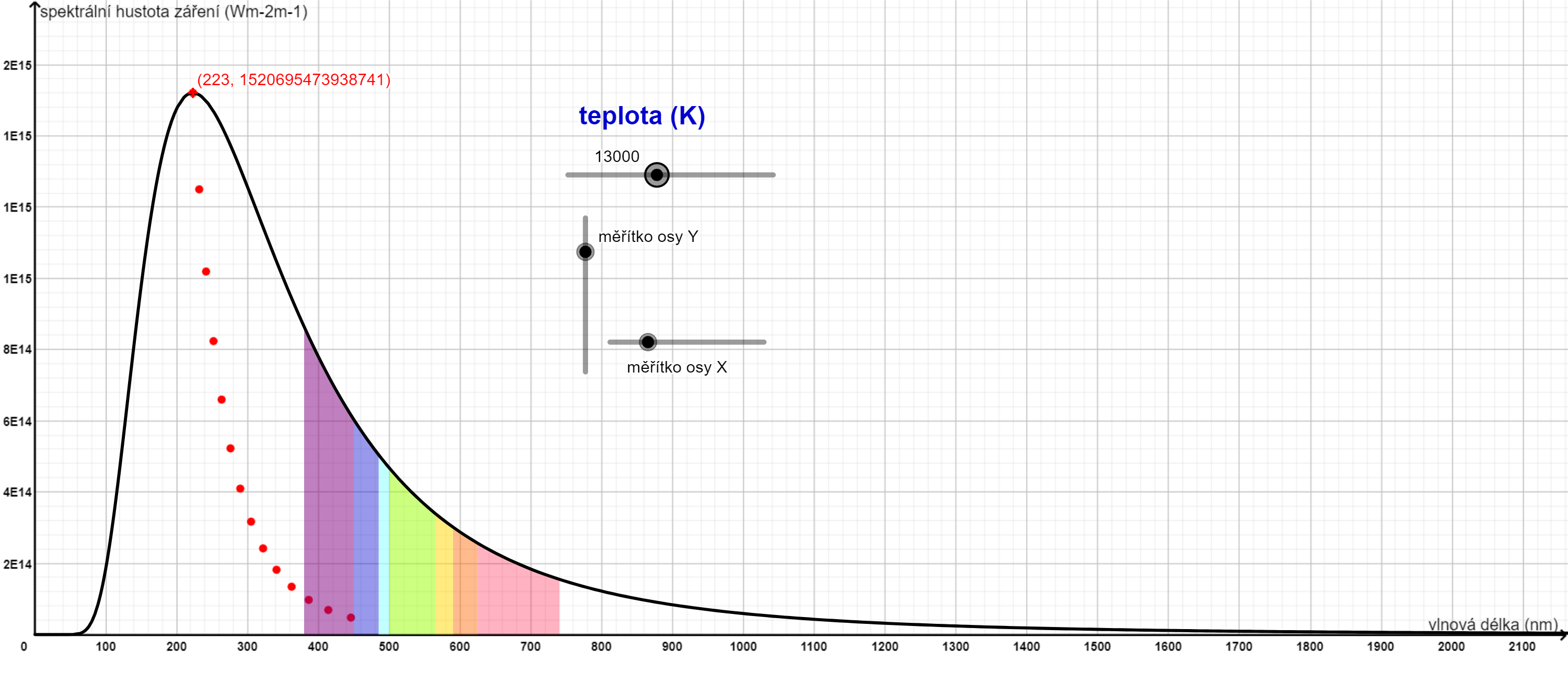
V následujícím interaktivním grafu si můžeme prohlédnout, jak záření černého tělesa závisí na jeho teplotě. Na svislé ose vynášíme spektrální hustotu záření, což je množství energie připadající na jednotku vlnové délky a na vodorovné ose vlnovou délku. Vidíme, že černé těleso září na různých vlnových délkách s různou intenzitou.
Zdroj
Při detailnějším zkoumání se všimneme, že s rostoucí teplotou černého tělesa, se zvětšuje obsah plochy pod křivkou a maximum záření se posouvá směrem do nižších vlnových délek. Dále tato pozorování popíšeme kvantitativně pomocí dvou jednoduchých vzorců.
Pomocí simulace znázorňující záření absolutně černého tělesa určete vlnovou délku v nm odpovídající maximu záření při teplotě 10 000 K.
První pozorování je popsáno Stefanovým-Boltzmannovým zákonem, který říká, že intenzita vyzařování černého tělesa je úměrná čtvrté mocnině termodynamické teploty.
Matematicky zapíšeme:
\[ I = \sigma T^4\;, \]přičemž \(I\) je intenzita vyzařování černého tělesa a \(T\) jeho termodynamická teplota. Konstanta úměrnosti mezi intenzitou vyzařování a termodynamickou teplotou je Stefanova-Boltzmannova konstanta o velikosti \(\sigma=5{,}67\cdot10^{-8}\ \mathrm{W}\cdot\mathrm{m}^{-2}\cdot\mathrm{K}^{-4}\). Chceme-li vyjádřit celkový zářivý výkon tělesa, musíme intenzitu záření vynásobit jeho plochou \(S\), Dostáváme tedy \(P=SI=S\sigma T^4\).
Druhým experimentálním faktem je Wienův posunovací zákon. Jeho obsahem je vztah mezi vlnovou délkou maxima záření absolutně černého tělesa a termodynamickou teplotou. Podle tohoto zákona ve tvaru \(\lambda_\mathrm{max}=b/T\) je vlnová délka maxima záření \(\lambda_\mathrm{max}\) absolutně černého tělesa nepřímo úměrná termodynamické teplotě \(T\). Konstanta úměrnosti má velikost \(b=2{,}898\cdot10^{-3}\ \mathrm{m}\cdot\mathrm{K}\).
Teplejší objekty září více v oblasti UV nebo třeba i RTG záření, zatímco chladnější objekty mají maximum záření v oblasti viditelného nebo infračerveného záření. Tyto poznatky nám umožňují například určit na základě spektra hvězdy její teplotu nebo bezkontaktně měřit teplotu povrchu různých těles.
Určete vlnovou délku, na jaké nejvíce září člověk.
Uvažujme teplotu člověka kolem 37 °C, což odpovídá 310 K. Vlnovou délku maxima záření černého tělesa při teplotě 310 K vypočítáme dosazením do vztahu
\[ \lambda_\mathrm{max} = \frac bT = \frac{2{,}898\cdot10^{-3}}{310}\ \mathrm{m} = 9{,}3\cdot10^{-6}\ \mathrm{m} = 9{,}3\ \mu\mathrm{m}\;. \]Určete celkový zářivý výkon Slunce, víte-li, že jeho povrchová teplota je 5 800 K.
Zářivý výkon určíme pomocí Stefanova-Boltzmannova zákona:
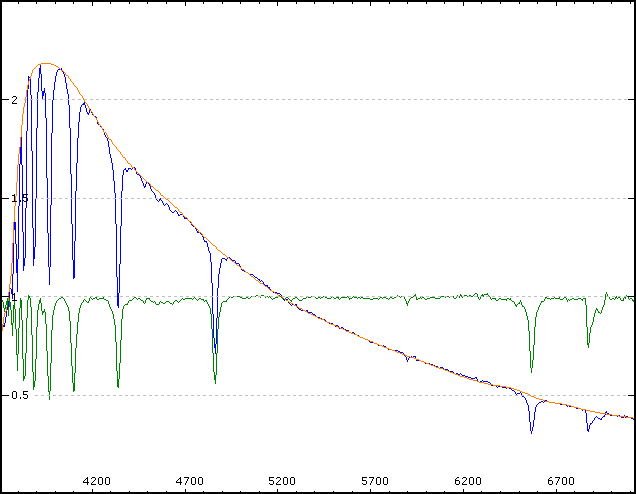
\[ P = SI = S\cdot\sigma T^4 = 4\pi R^2\cdot\sigma T^4 = 4\pi\cdot(7\cdot10^8)^2\cdot5{,}67\cdot10^{-8}\cdot5800^4=4\cdot10^{26}\ \mathrm{W}\;. \]Určete povrchovou teplotu hvězdy Sirius na základě analýzy jejího spektra. Výsledek porovnejte s její teplotou udávanou v odborné literatuře.
Zdroj
Nejprve je potřeba určit, pro kterou vlnovou délku je intenzita záření vysílaného hvězdou maximální. Tuto hodnotu, \(\lambda_\mathrm{max}=3900\ \hbox{Å}=390\ \mathrm{nm}\), odečteme jako vlnovou délku odpovídající maximu spektrální křivky. Dosazením do Wienova posunovacího zákona pak určíme teplotu hvězdy:
\[ T = \frac{b}{\lambda_\mathrm{max}} = \frac{2{,}898\cdot10^{-3}}{390\cdot10^{-9}}\ \mathrm{K} = 7430\ \mathrm{K}\;. \]Tato vypočítaná teplota poměrně dobře odpovídá hodnotám uvedeným v tabulce na obrázku 26.25.

