V předchozích kapitolách jsme se snažili popsat pohyb těles pomocí sil, kterými na sebe působí. Nyní se seznámíme s jiným způsobem popisu přírody – pomocí práce a energie. Jsou to běžně používané pojmy. Často říkáme, že člověk vykonal nějakou práci, nebo že má hodně energie. Zároveň se ale jedná o fyzikální veličiny, které je nutné správně definovat (ne vždy, když pracujete, konáte také práci ve fyzikálním slova smyslu). Pojďme se proto ponořit do studia těchto tajuplných veličin.
Mechanická práce
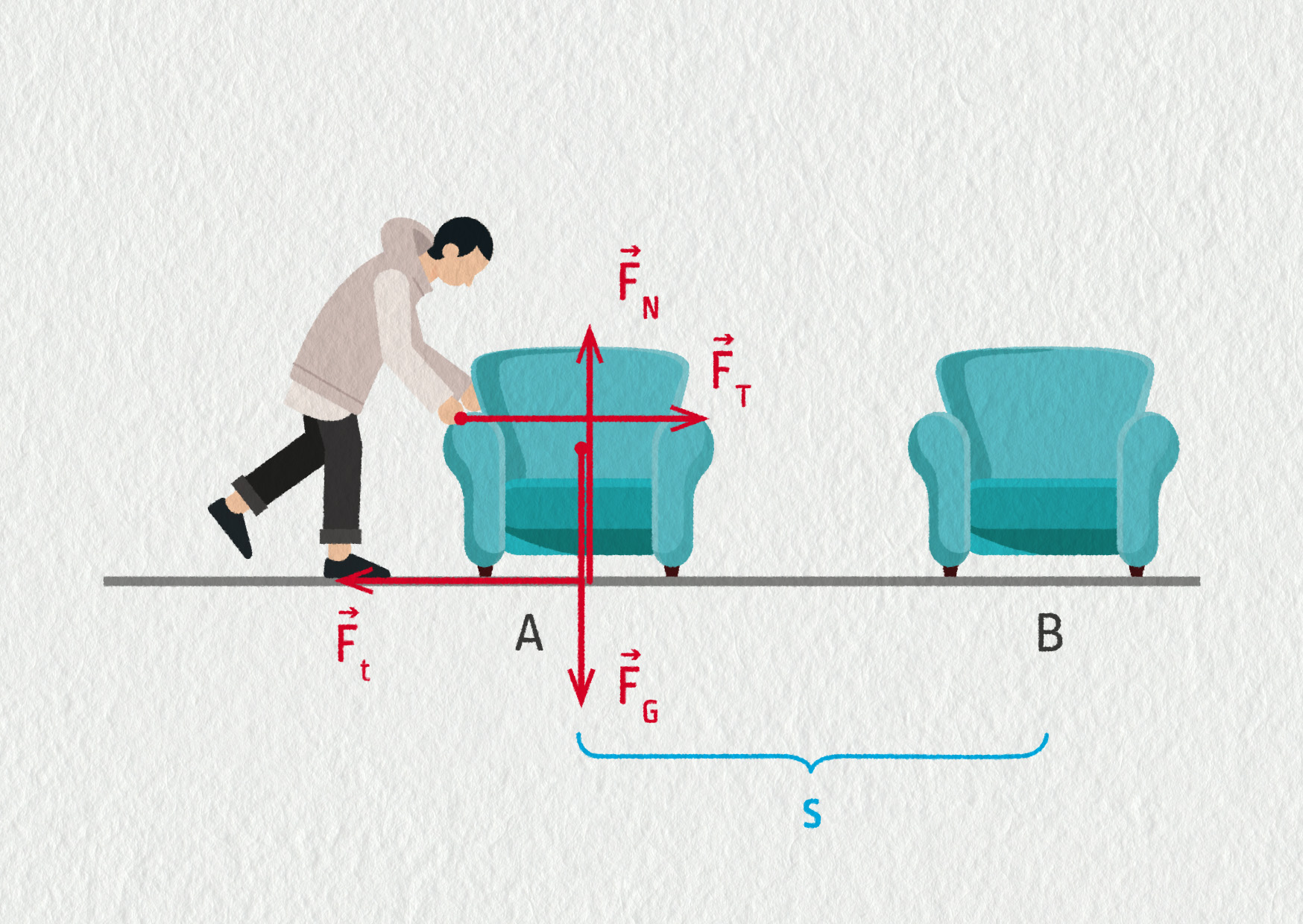
Studujme běžnou situaci, kdy člověk posunuje křeslo po podlaze.
Zdroj
Na křeslo působí čtyři síly: tíhová \(\Vec{F}_\mathrm{G}\), tlaková podložky \(\Vec{F}_\mathrm{N}\), tlaková síla člověka \(\Vec{F}_\mathrm{T}\), třecí síla \(\Vec{F}_\mathrm{t}\). Vlivem těchto sil se těleso posune z bodu A do bodu B čili urazí dráhu s. Tlaková síla \(\Vec{F}_\mathrm{T}\) tlačí křeslo dopředu, působí ve směru posunutí. Kdyby působila jen ona, pohyb by se zrychloval. Třecí síla \(\Vec{F}_\mathrm{t}\) působí proti směru pohybu, má tedy na pohyb opačný účinek – brzdí ho. Síly \(\Vec{F}_\mathrm{N}\) a \(\Vec{F}_\mathrm{G}\) působí kolmo na směr pohybu, vykompenzují se, čili neurychlují ani nebrzdí tento pohyb.
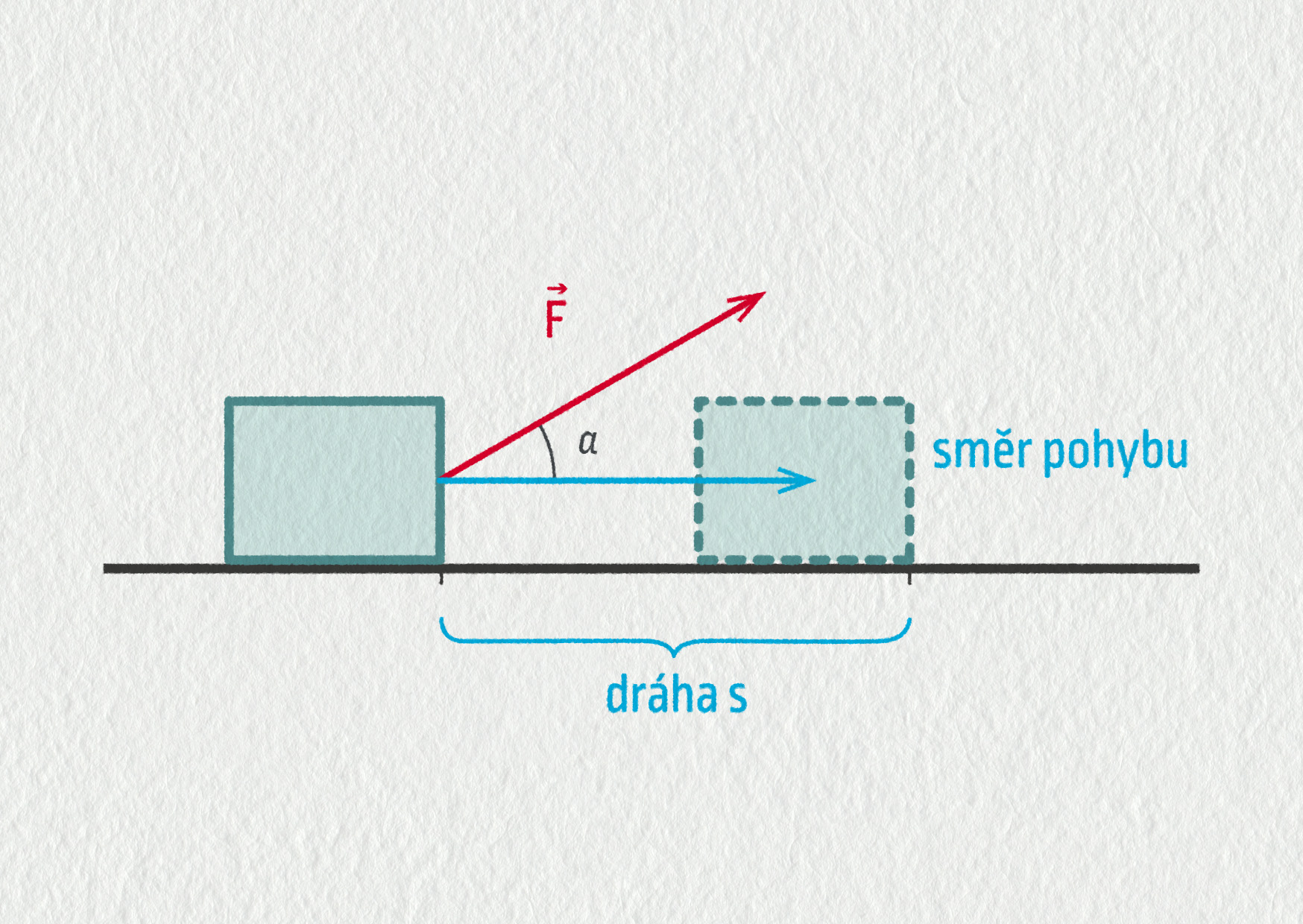
Chceme-li číselně vyjádřit, jakou energii daná síla předá tělesu na dráze s, definujeme veličinu
Definice mechanické práce
\[W_\mathrm{F} = Fs\cos\alpha\]
F ... velikost síly
s ... uražená dráha/posunutí
α ... úhel mezi silou a směrem pohybu
Poznámka: Uvedený vztah předpokládá konstantní sílu a neměnný úhel působení.
Zdroj
Jednotkou práce je joule J. Platí \(\mathrm{J=N\cdot m}\).
Práce se vždy vztahuje k určité síle; jde-li např. o třecí sílu \(\Vec{F}_\mathrm{t}\), píšeme \(W_\mathrm{t}=F_\mathrm{t}s\cos\alpha_\mathrm{t}\). Někdy se setkáme s formulací „člověk vykonal práci”. V tom případě se jedná o práci síly, kterou člověk působil na dané těleso. Pokud na těleso působí více různých sil, může každá síla konat jinou práci, které rozlišíme pomocí indexu.
Jak uvidíme později, práce je jeden ze způsobů, jak ukládat energii do tělesa.
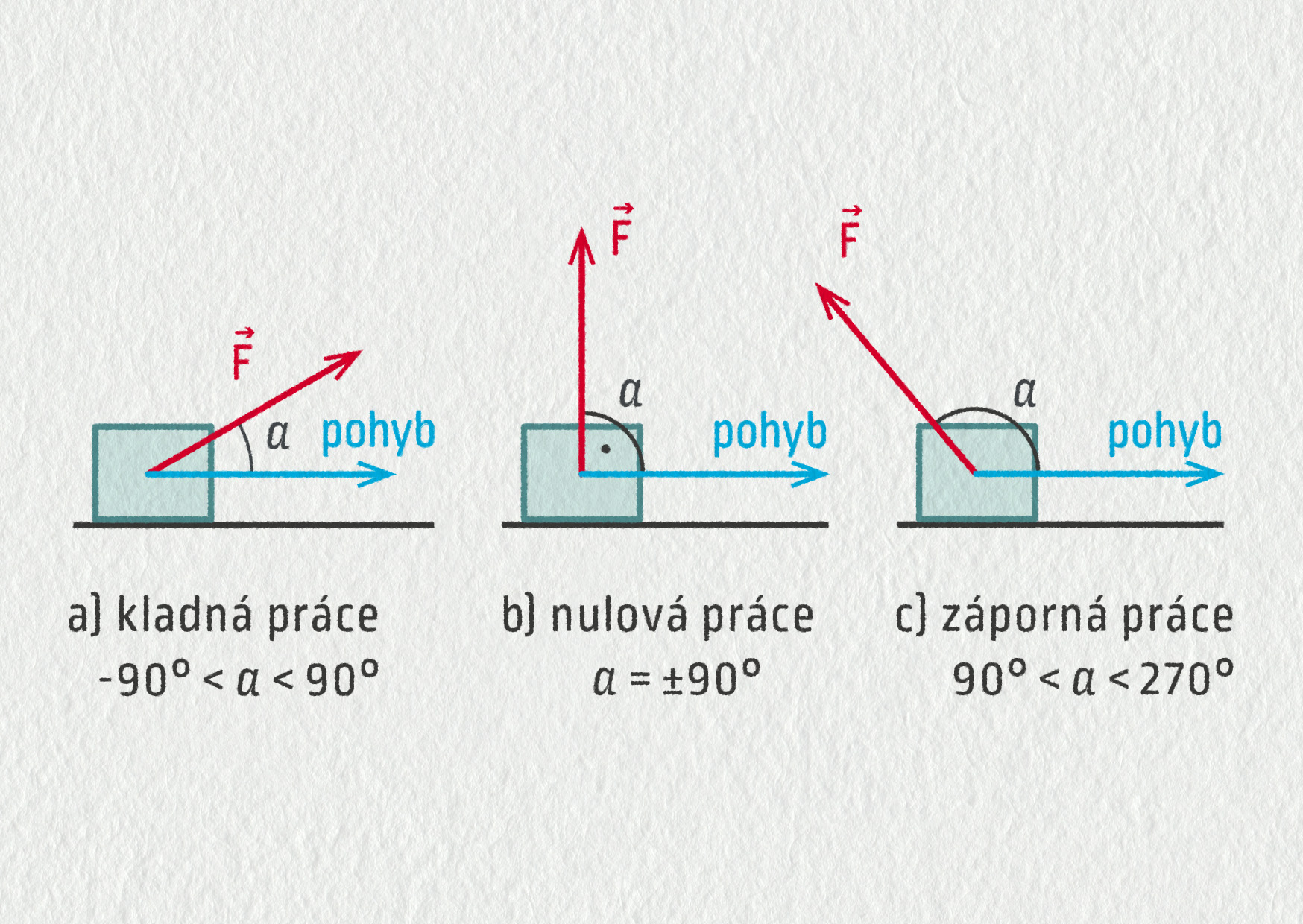
Síla může vykonávat kladnou, nulovou nebo dokonce zápornou práci. Záleží na tom, jaký směr svírá vektor síly \(\Vec{F}\) a směr pohybu (viz obrázek 6.8).
Zdroj
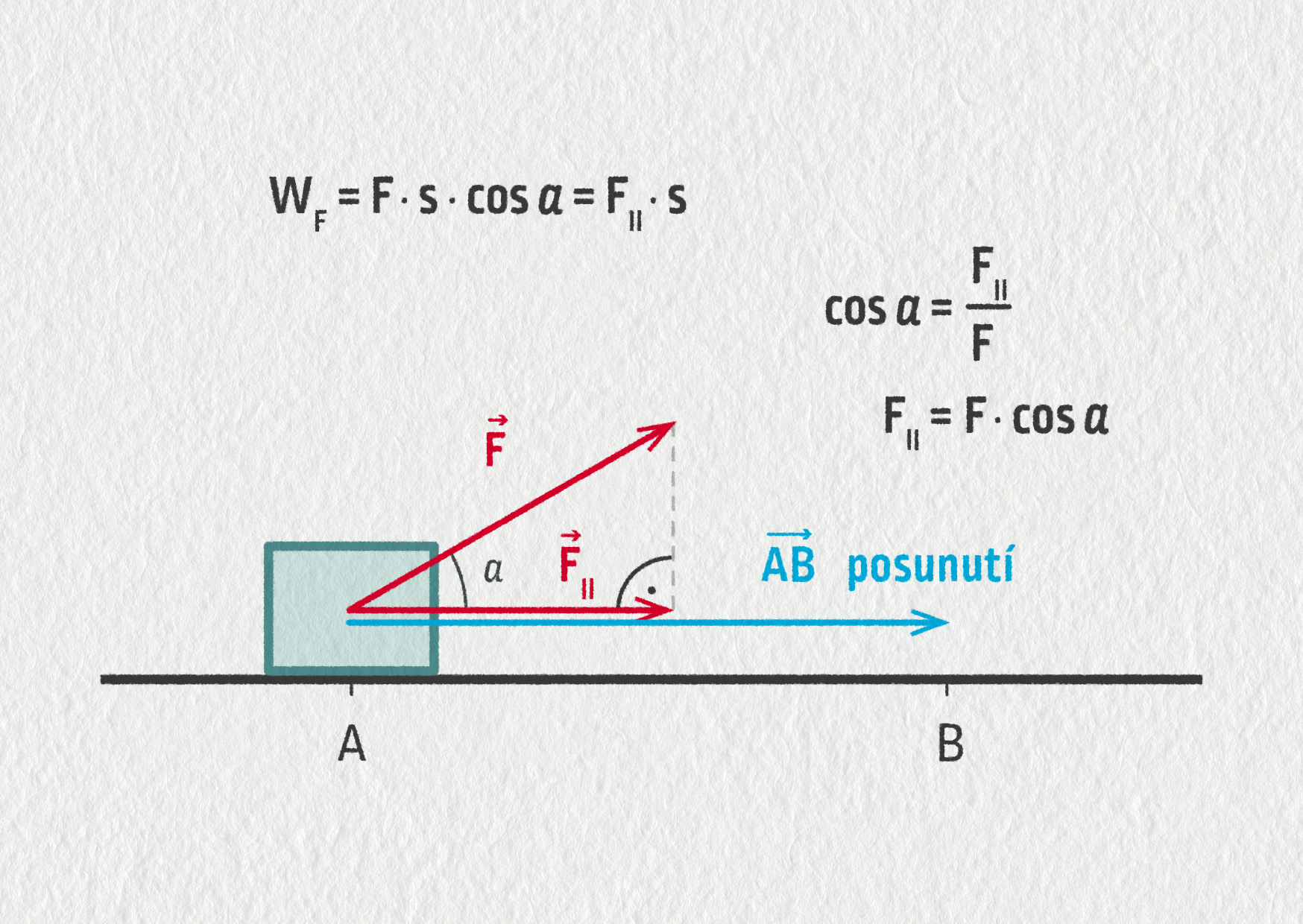
Nově zavedená veličina mechanická práce je zajímavá. Její velikost totiž závisí na úhlu α, který spolu svírají dva vektory: vektor síly \(\Vec{F}\) a vektor posunutí \(\overrightarrow{AB}\).
Píšeme: \(W_F=F\cdot|\overrightarrow{AB}|\cdot\cos\alpha\).
Když se na tuto situaci podíváme detailněji (viz obrázek), zjistíme, že část výrazu
o velikosti \(F\cos\alpha\) je průmětem vektoru síly do směru posunutí.
Zdroj
Výsledkem je číslo s fyzikální jednotkou (skalární veličina), které vyjadřuje, jak moc se síla podílí na změně rychlosti tělesa. Výraz \(W_F=F\cdot|\overrightarrow{AB}|\cdot\cos\alpha=F\cdot\cos\alpha\cdot|\overrightarrow{AB}|=F_\parallel\cdot|\overrightarrow{AB}|\) tak můžeme také chápat jako součin průmětu síly do směru posunutí a velikosti posunutí.
Právě tato vlastnost je v matematice popsána skalárním součinem dvou vektorů. Proto můžeme práci definovat jako skalární součin vektoru síly \(\Vec{F}\) a vektoru posunutí \(\overrightarrow{AB}\): \(W_F=\Vec{F}\cdot\overrightarrow{AB}\).
Skalární součin může být kladný, nulový nebo dokonce záporný, jak jsme viděli v obrázku 6.8. Teď již víme, že síla působí svým průmětem ve směru pohybu tělesa nebo proti jeho pohybu, tudíž ho urychluje, nebo naopak jeho rychlost snižuje.
V případě síly kolmé na posunutí síla pouze zakřivuje trajektorii jeho pohybu.
\(W_\mathrm{N}=F_\mathrm{N}s\cos 90^\circ =0\ \mathrm{J}\), protože \(\cos 90^\circ =0\).
\(W_\mathrm{G}=F_\mathrm{G}s\cos 90^\circ =0\ \mathrm{J}\), protože opět \(\cos 90^\circ =0\).
Těleso se stále dotýká podložky, ve svislém směru se nepohybuje čili podle zákona setrvačnosti se musí vyrušit síla gravitační s tlakovou silou podložky, \(F_\mathrm{N}=F_\mathrm{G}=m\cdot g=160\ \mathrm{N}\).
Velikost třecí síly určíme ze vztahu \(F_\mathrm{t}=fF_\mathrm{N}=0{,}25\cdot160\ \mathrm{N}=40\ \mathrm{N}\). A protože jde o pohyb rovnoměrný, velikost třecí síly \(F_\mathrm{t}\) je rovna velikosti tlakové síly \(F_\mathrm{T}\). Velikosti prací těchto sil pak závisí ještě na úhlu, který spolu působící síla a směr pohybu svírají.
\[W_\mathrm{t} = F_\mathrm{t}s\cos 180^\circ =\, 40\cdot3\cdot(-1)\ \mathrm{J} = -120\ \mathrm{J}\] \[W_\mathrm{T} = F_\mathrm{T}s\cos 0^\circ =\, 40\cdot3\cdot1\ \mathrm{J} = 120\ \mathrm{J}\]Tatínek jde spolu s malým Martinem sáňkovat. Martin má hmotnost 16 kg a táhne sáňky o hmotnosti 4 kg na provazu, jehož směr je rovnoběžný se zasněženou loukou. Koeficient tření mezi saněmi a sněhem je 0,1.
- Vypočítejte, jakou práci Martin vykoná při tažení saní na louce dlouhé 80 m.
- Vypočítejte, jak velkou práci vykoná na stejné dráze Martinův tatínek, který je vyšší, táhne silou 4,3 N a provaz saní svírá se směrem pohybu úhel 30°.
- Jakou práci vykoná tatínek, když tentokrát vezme saně na ramena a vůbec je netáhne?
- Velikost tahové síly odpovídá (1. Newtonův zákon) velikosti třecí síly mezi saněmi a sněhem. \(F_\mathrm{tah} = F_\mathrm{t} = fF_\mathrm{N} = fmg = 0{,}1\cdot4\cdot9,8\ \mathrm{N} = 3{,}9\ \mathrm{N}\). Pro práci vykonanou tahovou silou platí: \(W_\mathrm{tah} = F_\mathrm{tah}s = 3{,}9\cdot80\ \mathrm{J} = 312\ \mathrm{J}\).
- Práci, kterou vykoná tatínek, vyjádříme vztahem \(W_\mathrm{tat} = F_\mathrm{tat}s\cos 30^\circ \). Po dosazení: \(W_\mathrm{tat}=4{,}3\cdot80\cdot30^\circ\ \mathrm{J}=297\ \mathrm{J}\). Tatínek vykoná menší práci, protože při tažení saní pod úhlem α je trochu nadzvedává, a saně jsou tedy brzděny menší třecí silou, kterou musíme překonávat.
- Jestliže tatínek vezme saně na ramena, působí na ně silou, která je kolmá ke směru pohybu, a z našeho pohledu tedy práci nekoná. Chceme-li vysvětlit, proč je potom unavený, musíme si uvědomit, že člověk se při chůzi mírně pohupuje. Jeho těžiště se peridodicky zvedá a zase klesá o přibližně 5 cm. Síla, kterou tatínek drží saně na rameni, tedy také koná práci, a dokonce opakovaně. Další faktor, který bychom měli započítat, je také únava svalů. Svalová vlákna, držíme-li nějaký předmět, jsou napnuta, ale po určité době je musíme uvolnit, abychom je mohli znovu použít. Únava svalů tedy pramení také z tohoto mikroskopického zapínání svalových vláken. Ani tato mikroskopická práce není v našem fyzikálním vzorci započtena.
Osobní automobil o hmotnosti 1100 kg sjel bez brzdění z kopce dolů úsek silnice o délce 200 m (viz obrázek). Proti jeho pohybu působila průměrná odporová síla 300 N. Vypočítejte práci každé ze sil, které na něj působily.
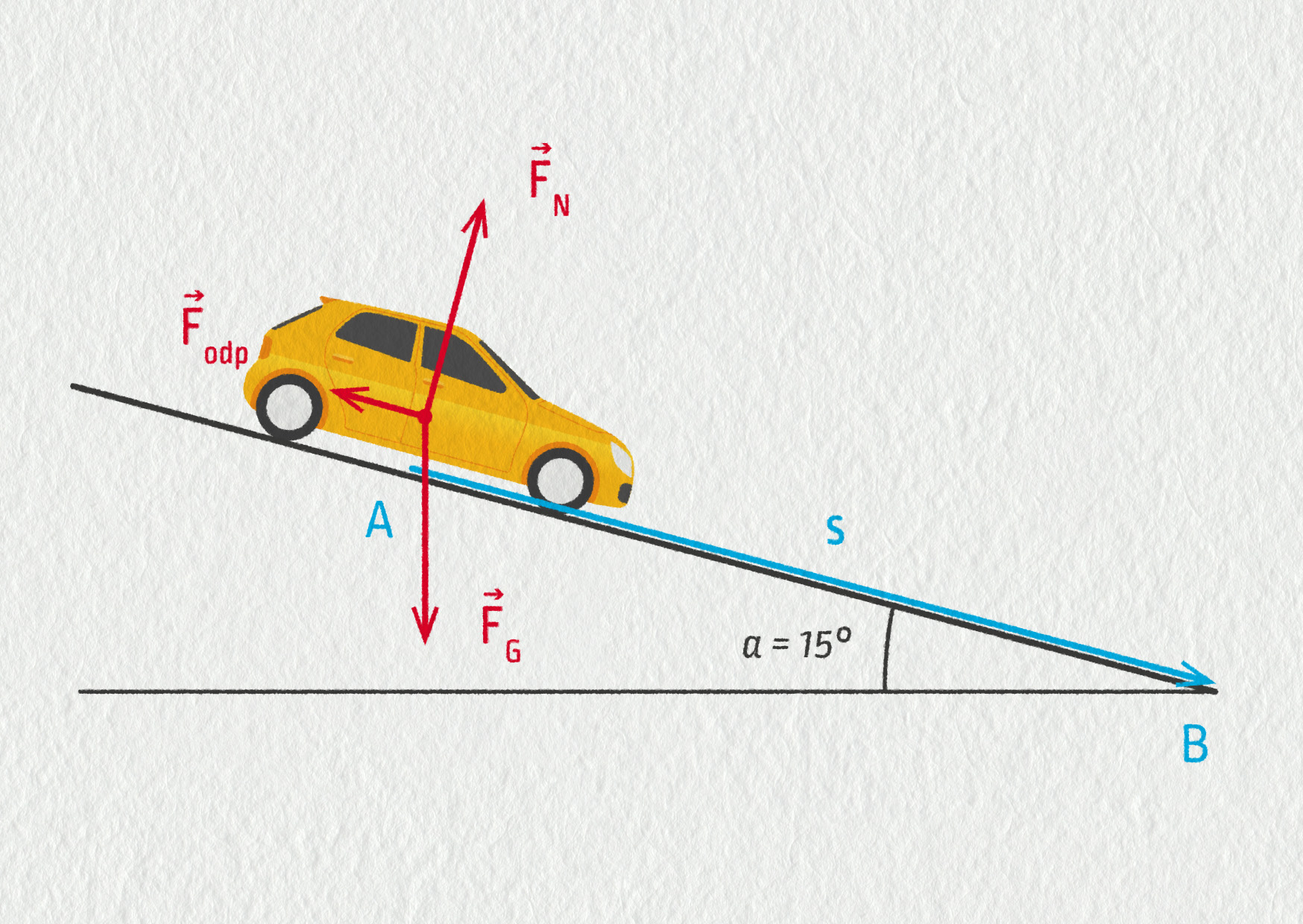
Zdroj
\(W_\mathrm{G}=F_\mathrm{G}s\cos 90^\circ \alpha)=570\ \mathrm{kJ}\), \(W_\mathrm{N}=0\), protože vektor síly je kolmý na směr posunutí, \(W_\mathrm{odp}=F_\mathrm{odp}s\cos 180^\circ =-F_\mathrm{odp}s = -60\,000\ \mathrm{J}=-60\ \mathrm{kJ}\).
Doposud jsme v našich úvahách počítali pouze se silami, které působí různými směry, ale mají stále stejnou velikost. Dokážeme spočítat práci i v případě, že se velikost síly mění?
Ano, a není to nijak složité. Jestliže se velikost síly nijak nemění, je práce vykonaná silou na tělese rovna \(W=Fs\), což v grafu \(F=f(s)\) odpovídá obsahu vyznačeného obdélníku.

Zdroj
Předpokládejme nyní, že se velikost působící síly jednou změní. V první části působení (0 až \(x_1\)) má síla velikost \(F_1\), v druhé části působení (\(x_1\) až \(x_2\)) má síla velikost \(F_2\). V obrázku vidíme, že celková vykonaná práce je rovna součtu obsahů jednotlivých obdélníků.
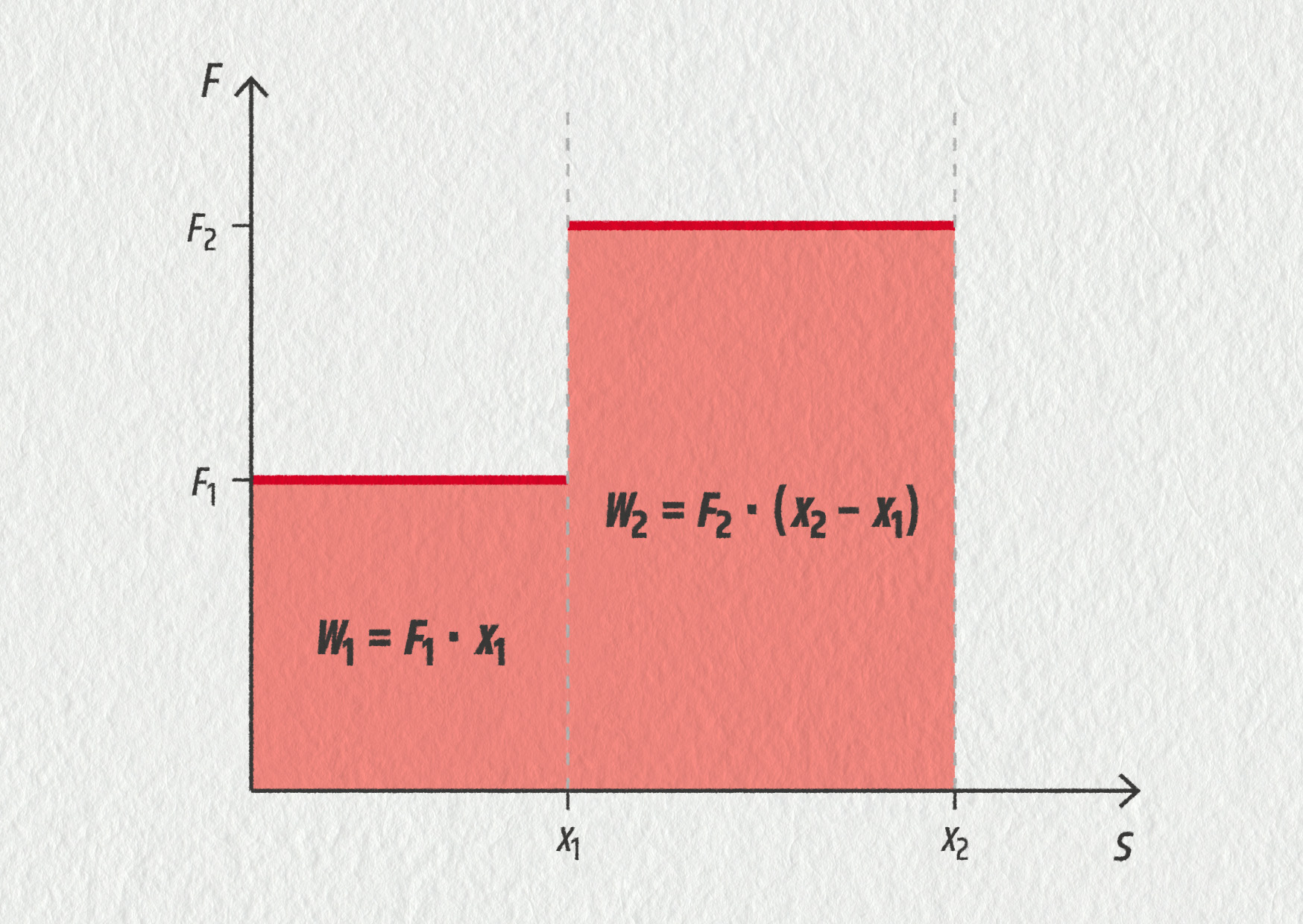
Zdroj
Pokud bude takových úseků více, vždy sečteme práce vykonané na jednotlivých úsecích. V případě spojitě se měnící síly mezi polohami \(x_1\) a \(x_2\) je velikost práce vykonané silou rovna obsahu plochy ohraničené polohami \(x_1\) a \(x_2\), křivkou a osou x. Podobnou úvahu jsme již využili v kapitole 3., kde jsme jako plochu pod grafem rychlosti v závislosti na čase získali uraženou vzdálenost.
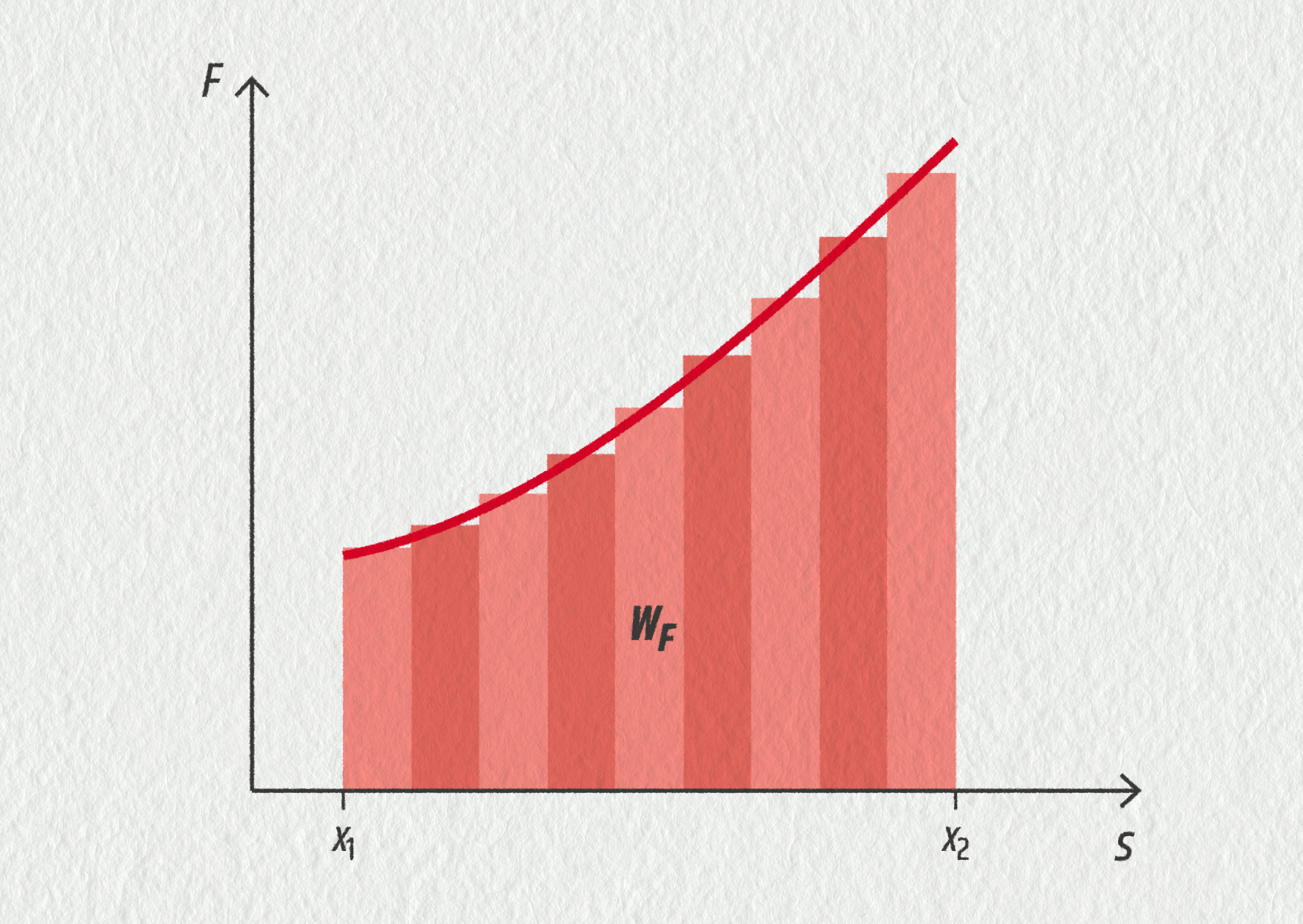
Zdroj

