Oko
V poslední části této kapitoly se budeme věnovat využití zobrazení v konkrétních optických přístrojích. Jednoznačně nejdůležitějším optickým „přístrojem“ je pro nás oko. Lidský zrak vyvinula evoluce do téměř dokonalé podoby a je pro nás nejdůležitějším smyslem. Pojďme nyní prozkoumat jeho fungování. K vytvoření zrakového vjemu jsou potřeba tři kroky:
- Optické zobrazení
- Přeměna světla na nervový vzruch
- Zpracování obrazu
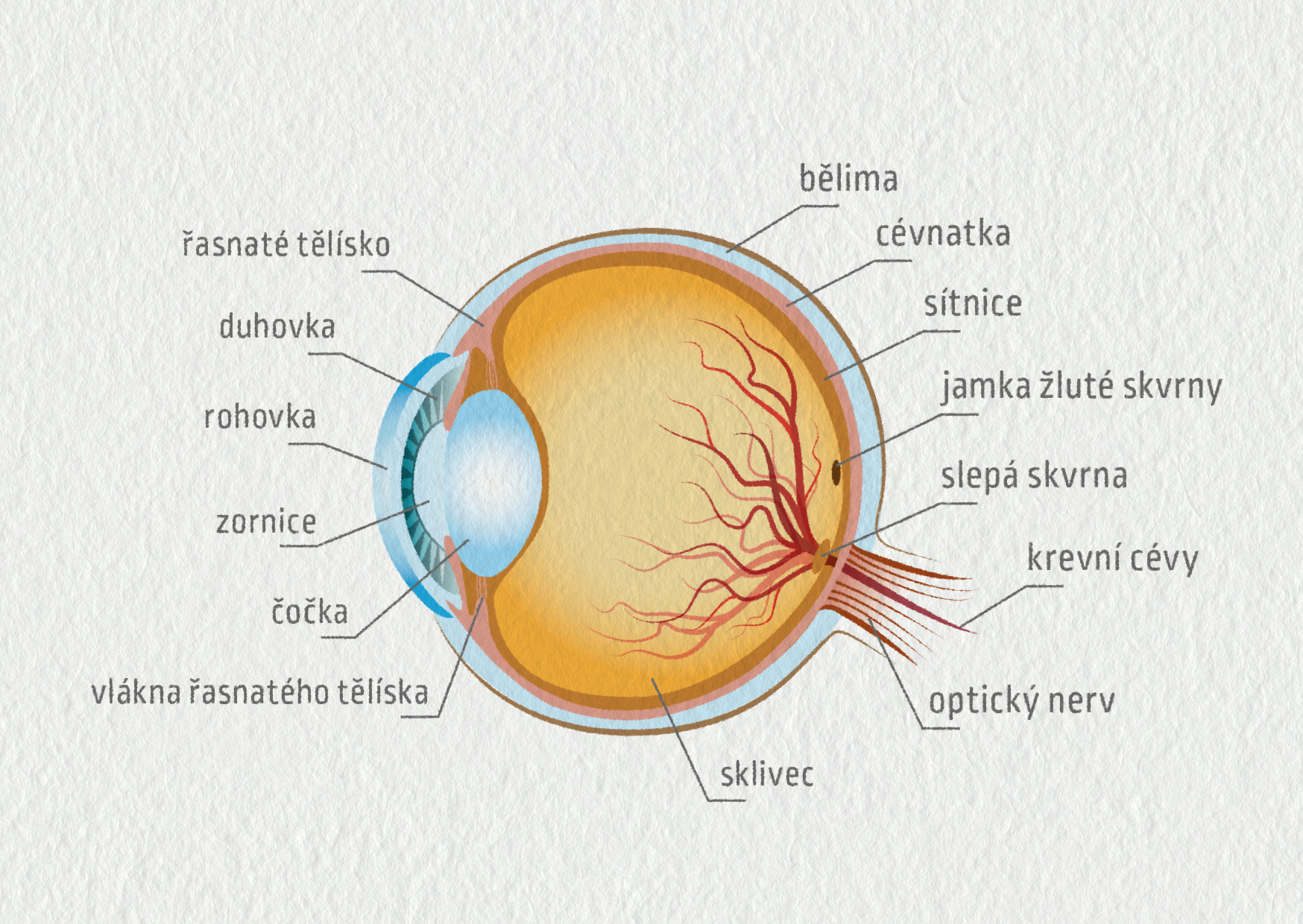
Oko slouží k vytvoření ostrého obrazu a jeho přeměně na nervový vzruch. Zpracování obrazu se pak děje v mozku. Nejdůležitější části oka vidíte na obrázku 23.52.
Zdroj
Oko se chová jako spojka s proměnnou ohniskovou délkou. Vytváří skutečný zmenšený a převrácený obraz skutečnosti. Lom světla probíhá na rohovce a na čočce, přičemž nejsilnější je hned první lom na rozhraní vzduch – rohovka. Zatímco tvar rohovky je stálý, čočka se může deformovat a tím mírně měnit svoji optickou mohutnost. Deformaci čočky (akomodaci) zajišťují svaly v řasnatém tělísku. Zdravé oko dokáže díky tomu vytvořit na sítnici ostrý obraz předmětů ve vzdálenostech zhruba od 20 cm do nekonečna.
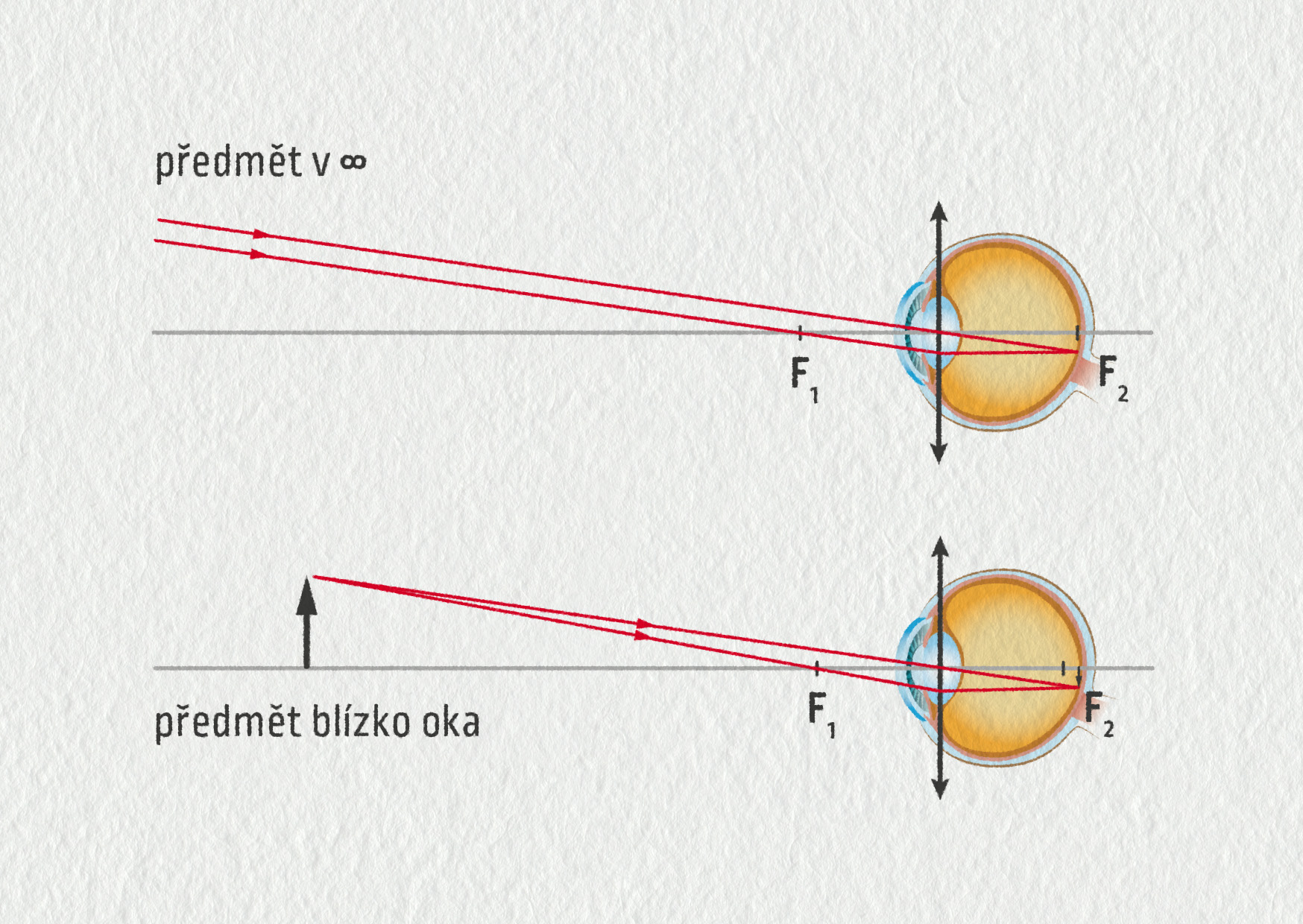
Zdroj
Průměr oční koule člověka je cca 2 cm. Na základě tohoto údaje určete, jaká je přibližně optická mohutnost oka. Napište hodnotu v dioptriích:
Ohnisková délka musí odpovídat průměru oka, proto \(f=0{,}02\ \mathrm{m}\) a \(\varphi=1/f=50\ \mathrm{D}\). Optická mohutnost oka je ve skutečnosti cca 60 D.
Pro konkrétní oko definujeme blízký bod – minimální vzdálenost předmětu, který dokáže oko ještě zaostřit. A naopak vzdálený bod – maximální vzdálenost předmětu, který dokáže zaostřit. Pokud není váš vzdálený bod v nekonečnu, poznáte to jednoduše tak, že vzdálené předměty nevidíte zcela ostře. Blízký bod si můžete snadno změřit sami. Vezměte nějaký text a najděte nejmenší vzdálenost, ze které na něj dokážete zaostřit. Možná jste si všimli, že zaostřování na velmi krátkou vzdálenost je trochu nepříjemné. Je to tím, že čočku je třeba deformovat do krajní polohy. Proto byla dohodou stanovena vzdálenost, ze které byste měli být schopni číst pohodlně bez zbytečného namáhání oka:
Konvenční zraková vzdálenost \(d=25\ \mathrm{cm}\).
Podle polohy blízkého a vzdáleného bodu rozlišujeme dvě nejčastější oční vady:
Krátkozrakost (myopie)
Hlavním příznakem krátkozrakosti je neostré vidění na větší vzdálenosti. Vzdálený bod oka je blíž než v nekonečnu. Je to tím, že paprsky se sbíhají už před sítnicí, a na sítnici tedy nevzniká ostrý obraz. Krátkozrakost se napravuje rozptylkou, která sníží optickou mohutnost oka a posune ostrý obraz na sítnici.
Myopie je nejčastěji způsobena špatnou anatomií oka, kdy jeho velikost neodpovídá optické mohutnosti. Vada se proto vyvine většinou během dospívání. Zajímavé je, že krátkozrakost je typická civilizační nemoc. V Evropě už postihuje víc jak čtvrtinu obyvatel a toto číslo neustále roste. Naopak u přírodních národů je myopie poměrně vzácná. Lékaři přišli na to, že na rozvoj myopie mají kromě genetiky zásadní vliv dva faktory. Jde o čas strávený venku a čas strávený zaostřením na blízký předmět (mobil, počítač, kniha).
Dalekozrakost (hyperopie)
Hlavním příznakem dalekozrakosti je nemožnost zaostřit blízké předměty (blízký bod je příliš daleko). Člověk potřebuje „brýle na čtení“. Optická mohutnost oka je příliš malá a ostrý obraz vzniká až za sítnicí. Proto se dalekozrakost napravuje spojkou.
Hyperopie nejčastěji vzniká tak, že s přibývajícím věkem klesá pružnost oční čočky a ta se již nedokáže dostatečně deformovat. Špatná zpráva pro osoby s krátkozrakostí je, že dalekozrakost ji nekompenzuje. Člověk pak trpí oběma vadami současně a potřebuje dvoje brýle.
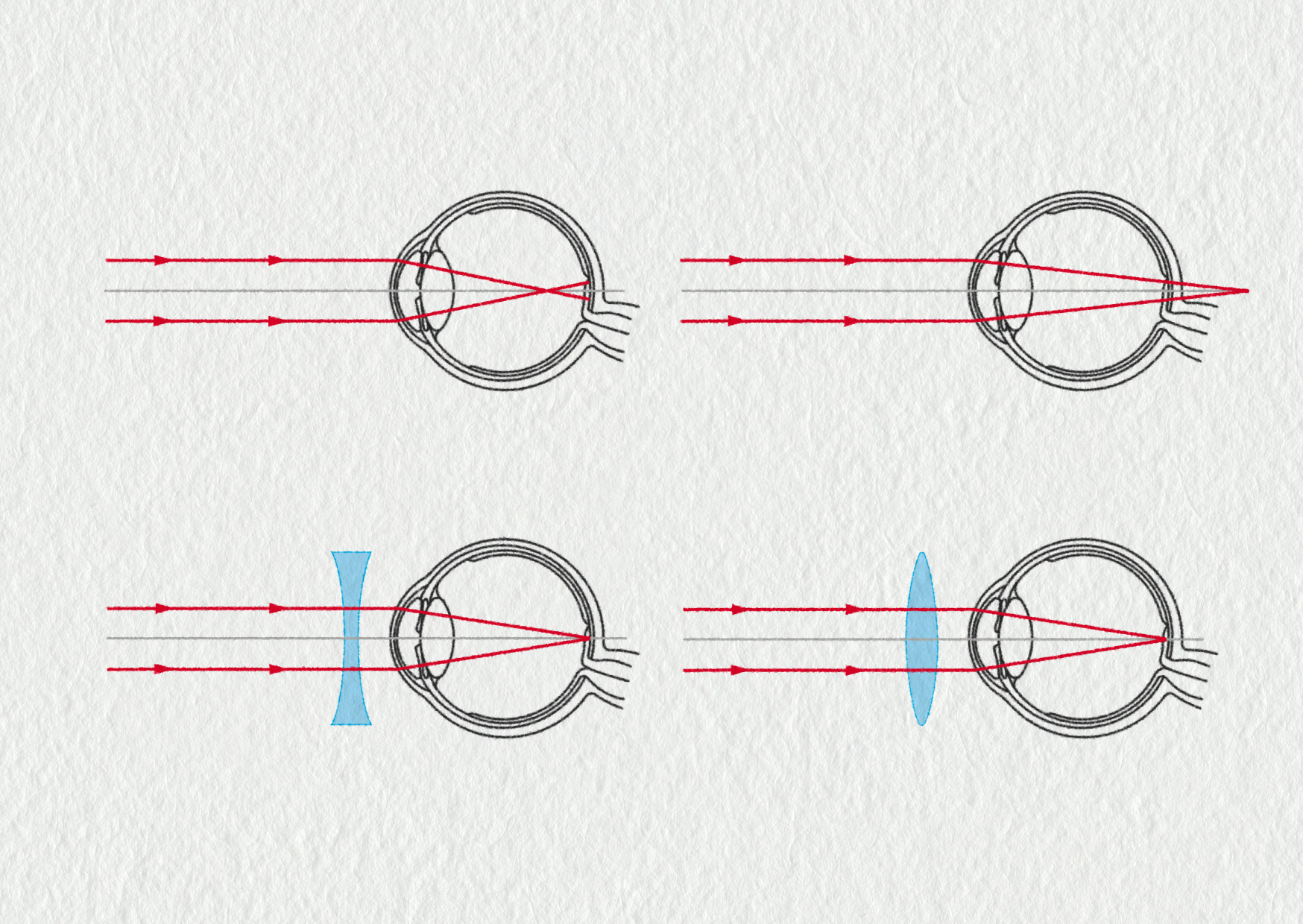
Zdroj
Martin už není nejmladší a trpí dalekozrakostí. Jeho oko má blízký bod ve vzdálenosti 70 cm. Pro práci na počítači a čtení potřebuje brýle. Vypočítejte, jakou optickou mohutnost brýlí bude Martin potřebovat, aby mohl zase číst z konvenční zrakové vzdálenosti 25 cm.
Předmět se nachází v oblasti, kam Martin nedokáže zaostřit. Role brýlí spočívá v tom, že vytvoří neskutečný obraz předmětu ve vzdálenosti, kam oko zaostřit dokáže. V tomto případě proto potřebujeme vytvořit neskutečný obraz předmětu ve vzdálenosti 70 cm před čočkou. K tomu použijeme spojku, kde \(a=25\ \mathrm{cm}\), \(a'=-70\ \mathrm{cm}\) (hodnota je záporná, protože obraz bude před čočkou). Tyto hodnoty můžeme dosadit do zobrazovací rovnice a vypočítat potřebnou ohniskovou délku \(f\):
\[\begin{aligned} \frac1a + \frac1{a'} &= \frac1f\\ \frac1f &= \frac{aa'}{a+a'} = 39\ \mathrm{cm} = 0{,}39\ \mathrm{m}\;.\\ \end{aligned}\]Optickou mohutnost pak určíme jako převrácenou hodnotu ohniskové délky: \(\varphi=1/f=2{,}6\ \mathrm{D}\).
Vraťme se ještě jednou k fungování zraku. K převodu světla na nervový vzruch slouží sítnice. Je tvořena dvěma druhy buněk, které reagují na světlo. Tyčinky jsou citlivější, ale reagují pouze na intenzitu světla. Pomocí tyčinek dokážeme vidět za šera. Čípky jsou méně citlivé, ale pro náš zrak důležitější, protože zajišťují barevné vidění (o barevném vidění se dočtete podrobněji v kapitole 24). Odhaduje se, že tyčinek je cca 120 miliónů, zatímco čípků jen asi 7 milionů. Čípky jsou však vysoce koncentrované do oblasti žluté skvrny, což je místo, kde optická osa oka protíná sítnici. Pouze v této malé části sítnice vzniká ostrý obraz. Celý zbytek sítnice slouží jen k perifernímu vidění. Tuto situaci ilustruje následující obrázek.

Zdroj
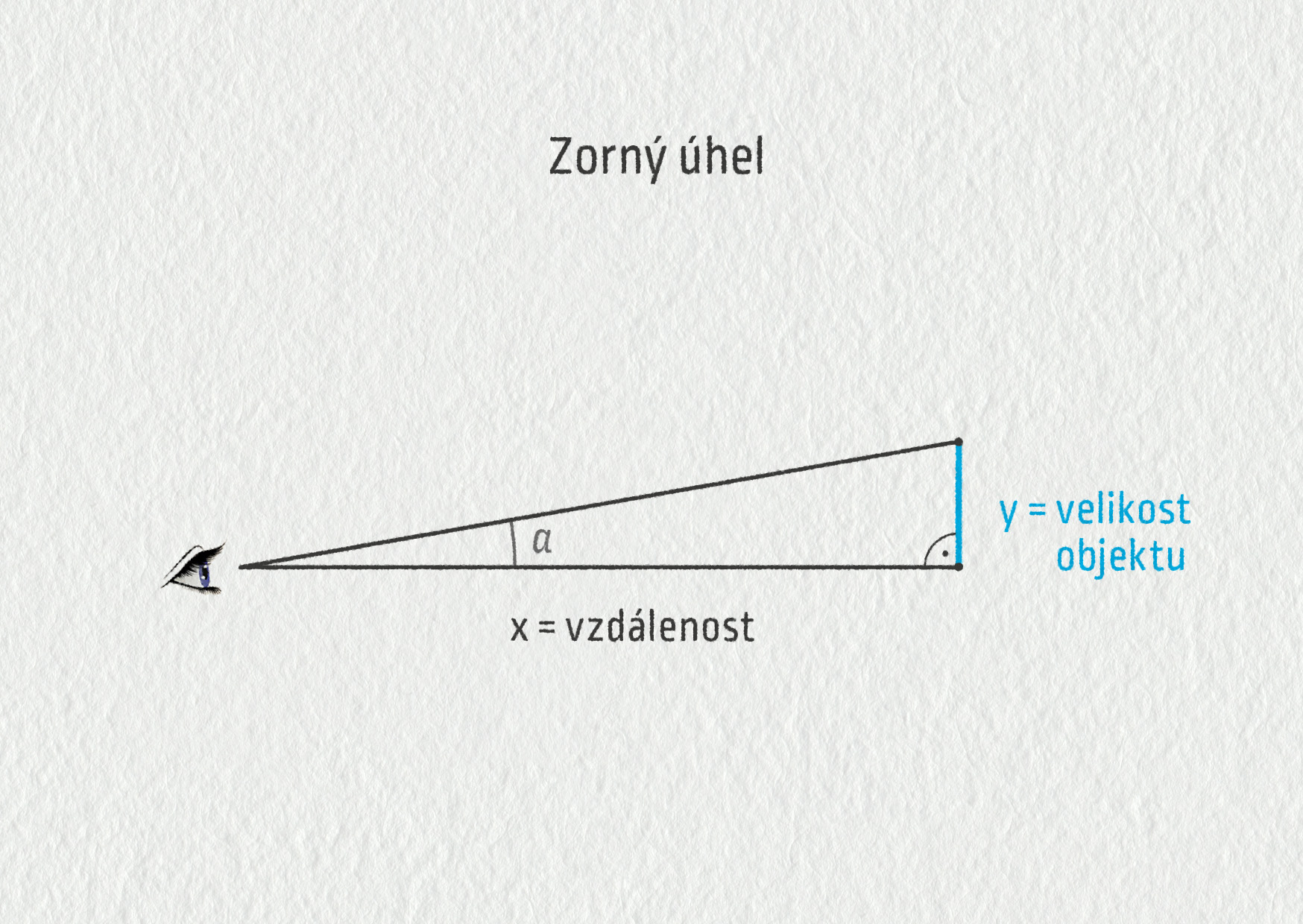
Hustota buněk na sítnici v oblasti žluté skvrny určuje, jak jemné detaily dokážeme rozlišit. Tento důležitý parametr se nazývá rozlišovací schopnost oka. Je definována pomocí zorného úhlu (viz obrázek 23.56).
Zdroj
Z obrázku vyplývá, že pro zorný úhel platí \(\tan\alpha=y/x\). Rozlišovací schopnost oka je definována jako minimální zorný úhel, pod kterým ještě dokážeme rozlišit dva body. Platí:
Rozlišovací schopnost oka \(\alpha_\mathrm{MIN}=1'=1/60^\circ\).
Pokud dosadíme do vztahu \(\tan\alpha=y/x\) hodnotu \(\alpha_\mathrm{MIN}=1'\), můžeme snadno vypočítat, jak velké objekty (jak vzdálené body) dokážeme rozeznat z určité vzdálenosti. Rozlišovací schopnost oka si můžete sami změřit v kapitole 24.
Vypočítejte, jak vzdálené body dokážeme okem rozlišit
- při čtení (\(x=d=25\ \mathrm{cm}\)),
- na druhém konci třídy (\(x=10\ \mathrm{m}\)),
- na Měsíci (\(x=380\,000\ \mathrm{km}\)).
Nejprve provedeme obecné řešení úlohy:
\[ \tan\alpha = \frac yx \quad\Rightarrow\quad y = x\tan\alpha = x\tan(1') = 0{,}000\,29\cdot x\;. \]Nyní dosadíme zadané vzdálenosti \(x\) a výsledky zaokrouhlíme:
- čtení: \(y=0{,}07\ \mathrm{mm}\)
- třída: \(y=3\ \mathrm{mm}\)
- Měsíc: \(y=100\ \mathrm{km}\)
Pomocí zorného úhlu určuje člověk také velikost předmětů. Ale pozor, jde o relativní, nikoliv absolutní velikost. Dobrým příkladem je Slunce a Měsíc. Oba objekty se nám jeví na obloze stejně velké, protože je pozorujeme oba přibližně pod stejným zorným úhlem cca 0,5°. Pokud však neznáme jejich vzdálenosti od Země, nelze jejich velikost srovnávat.
Na závěr se krátce zmíníme o zpracování obrazu v mozku. Informace z tyčinek a čípků putují zrakovým nervem do zrakového centra. V této části mozku probíhá třídění a zpracování informací. Uvažte, že „datový tok“, který přichází z očí do mozku je obrovský – odhaduje se že jde o několik desítek GB za sekundu. Centrum zraku funguje zjednodušeně řečeno tak, že rozpoznává v záplavě přicházejících dat známé tvary a přiřazuje jim určitý význam. Teprve takto filtrované a zjednodušené informace putují do našeho vědomí.

Zdroj
Fotoaparát
Fotoaparát (nebo kameru) můžeme považovat za technickou kopii lidského oka. Jejich význam je podobný – slouží k vytvoření zmenšeného skutečného obrazu reality. Následující obrázek 23.58 ukazuje „anatomii“ obvyklého fotoaparátu.
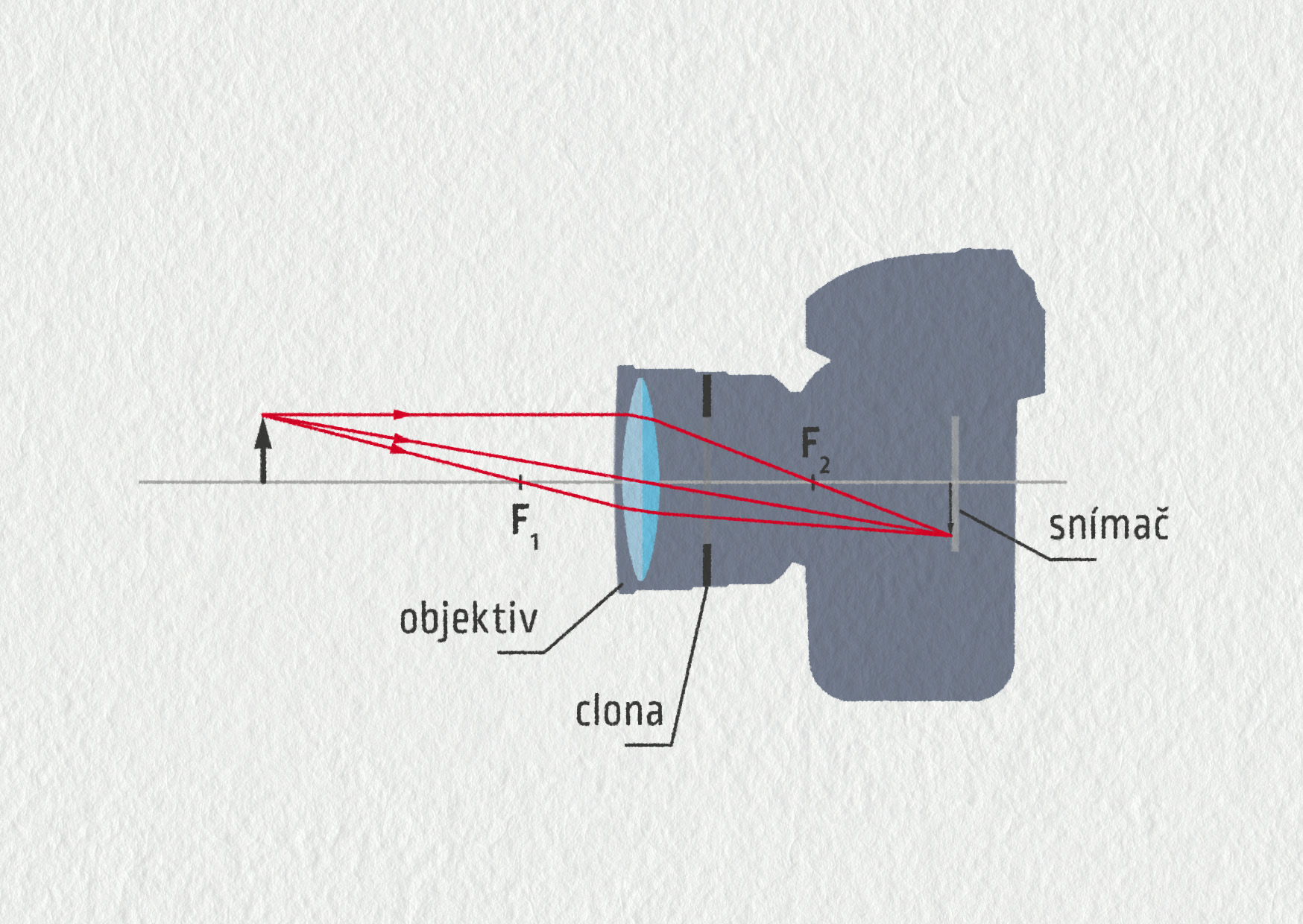
Zdroj
Objektiv může být v nejjednodušším případě tvořen jedinou spojkou, jako je na obrázku. Pokud je objektiv tvořen více čočkami, je jeho konstrukce složitější, ale význam zůstává stejný. Zaostřování se děje, narozdíl od oka, posunem čočky vůči snímači. Nejdůležitějším parametrem každého objektivu je jeho ohnisková délka. Objektiv s velkou ohniskovou délkou má úzký záběr a naopak (viz obrázek 23.59). Označení ZOOM pak znamená objektiv s měnitelnou ohniskovou délkou.
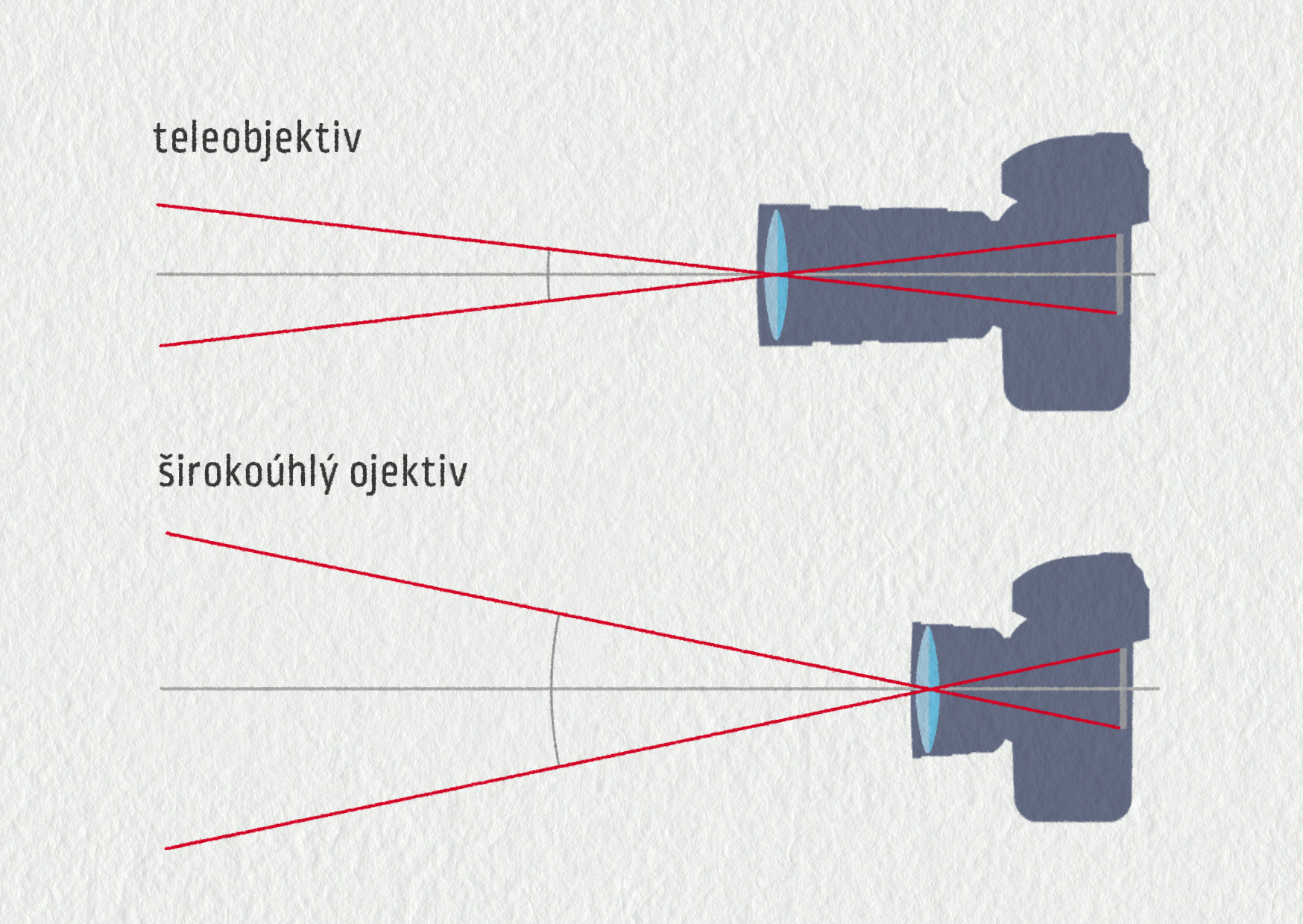
Zdroj
Clona je kruhový otvor s měnitelným průměrem a slouží k regulaci množství světla, dopadajícího na snímač (ke stejnému účelu slouží duhovka v oku). Množství světla, které dopadne na snímač, je dále možné ovlivnit ještě expozičním časem a také citlivostí snímače. V dnešních fotoaparátech a kamerách za nás správné nastavení osvětlení hlídá elektronika.
Snímač je tvořen speciálním typem čipu, který obsahuje velké množství „buněk“ tvořených fototranzistory. Jejich počet se u běžných snímačů pohybuje v nižších jednotkách milionů a udává se v jednotkách megapixel. Každý pixel má vyhrazeno celkem 24 bitů, to je \(2^{24}=16\,777\,216\) barevných odstínů. Ty vzniknou kombinací intenzity tří barevných kanálů (RGB) po 8 bitech. Více o barevném modelu RGB se dočtete v kapitole 24.
Vypočítejte, kolik MB informace obsahuje barevná fotografie s rozlišením 16 megapixelů.
\[ 24\ \hbox{bitů}\cdot16\cdot10^6\ \hbox{pixelů} = 384\cdot10^6\ \hbox{bitů} = 48\ \mathrm{MB}\;. \]
Poznámka: Ve skutečnosti vám tato fotografie zabere pouze něco kolem 6 MB, protože data se ukládají v komprimovaném formátu (např. JPEG). Komprese je pak naprostou nezbytností u videa, kde každou sekundu vznikne minimálně 24 takových obrázků.
Fotografie

Zdroj

Zdroj

Zdroj

Zdroj
Mikroskop a dalekohled
Na závěr se budeme věnovat přístrojům, které mají za úkol zvětšovat zorný úhel. Představte si, že stojíte 10 m daleko od nápisu, který si chcete přečíst. Písmena jsou malá a vy nápis nepřečtete, zorný úhel je příliš malý. Stačí přijít blíž, zorný úhel se zvětší a vy si můžete nápis v klidu přečíst. Problém nastane v případě, že pozorovaný předmět je tak malý, že blíž už oko dát nemůžete, neboť narazíte na blízký bod vašeho oka. V takovém případě potřebujete lupu nebo mikroskop. Někdy není problém ve velikosti předmětu, ale ve vzdálenosti. K hvězdě či planetě prostě blíž přijít nemůžete. V takovém případě budete potřebovat dalekohled. Zvětšení zorného úhlu popisujeme pomocí úhlového zvětšení. Je to poměr nového a původního zorného úhlu.
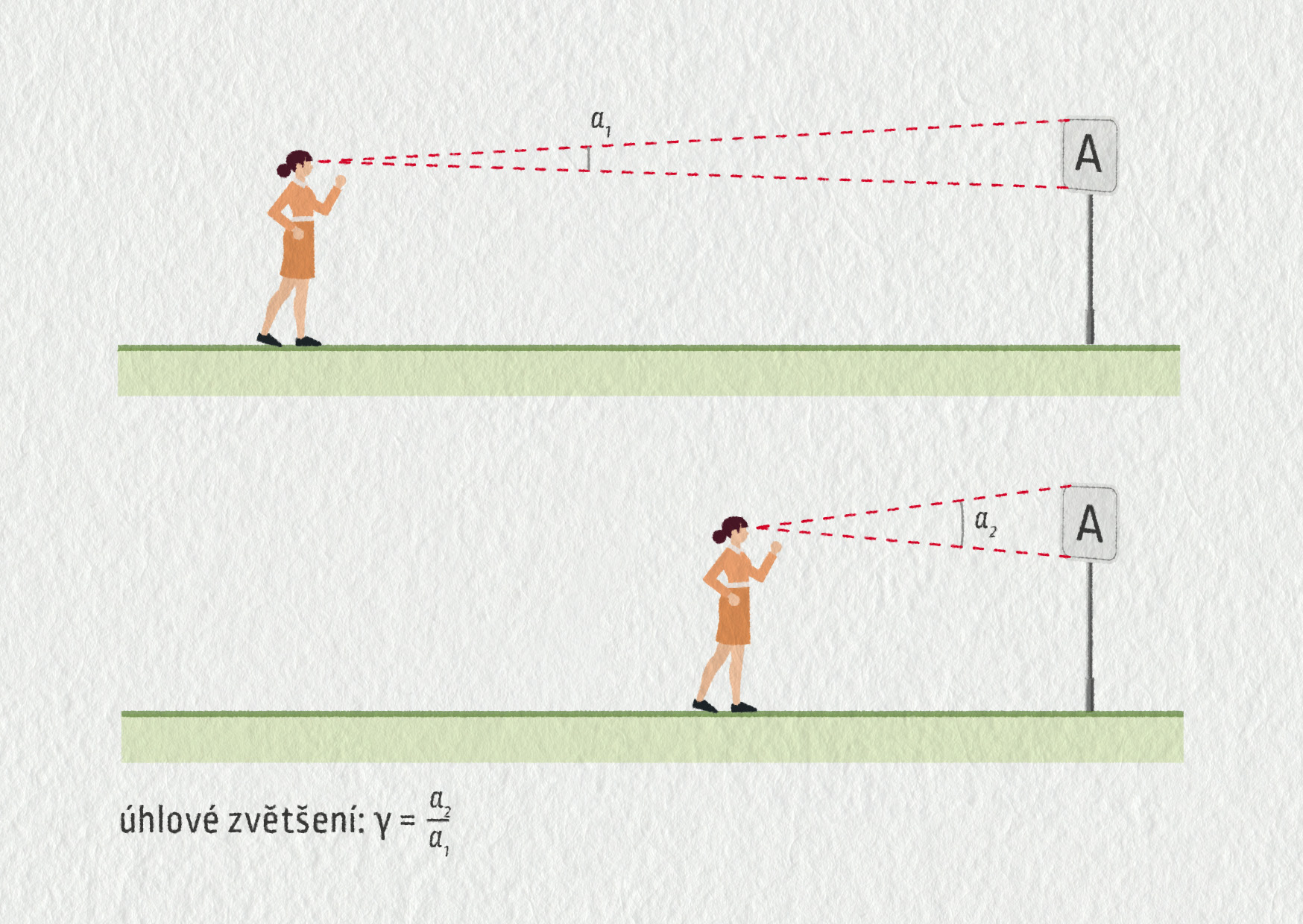
Zdroj
Lupu používáme tak, že pozorovaný předmět umístíme do ohniska spojky. Dejme tomu, že máme hodinářskou lupu s ohniskovou délkou 5 cm a pozorovaný předmět má velikost 4 mm.
- Pomocí konstrukce nebo výpočtu určete, vlastnosti a polohu obrazu vytvořeného lupou.
- Vypočítejte zorný úhel, pod jakým pozorujeme předmět pomocí lupy.
- Vypočítejte zorný úhel, pod jakým pozorujeme předmět bez lupy z konvenční zrakové vzdálenosti \(d=25\ \mathrm{cm}\).
- Určete úhlové zvětšení lupy.
- Dokažte, že pro úhlové zvětšení lupy platí jednoduchý přibližný vztah \(\gamma=d/f\), kde \(d\) je konvenční zraková vzdálenost a \(f\) je ohnisková délka použité čočky.
a) Použijeme-li zobrazovací rovnici a dosadíme \(f=50\ \mathrm{mm}\), \(a=50\ \mathrm{mm}\), Vyjde nám, že \(a'\) nelze vypočítat, neboť ve zlomku dělíme nulou. Fyzikálně to znamená, že obraz vzniká v nekonečnu. Pro snadnější vyřešení dalších otázek bude dobré si vytvořit náčrtek této situace.
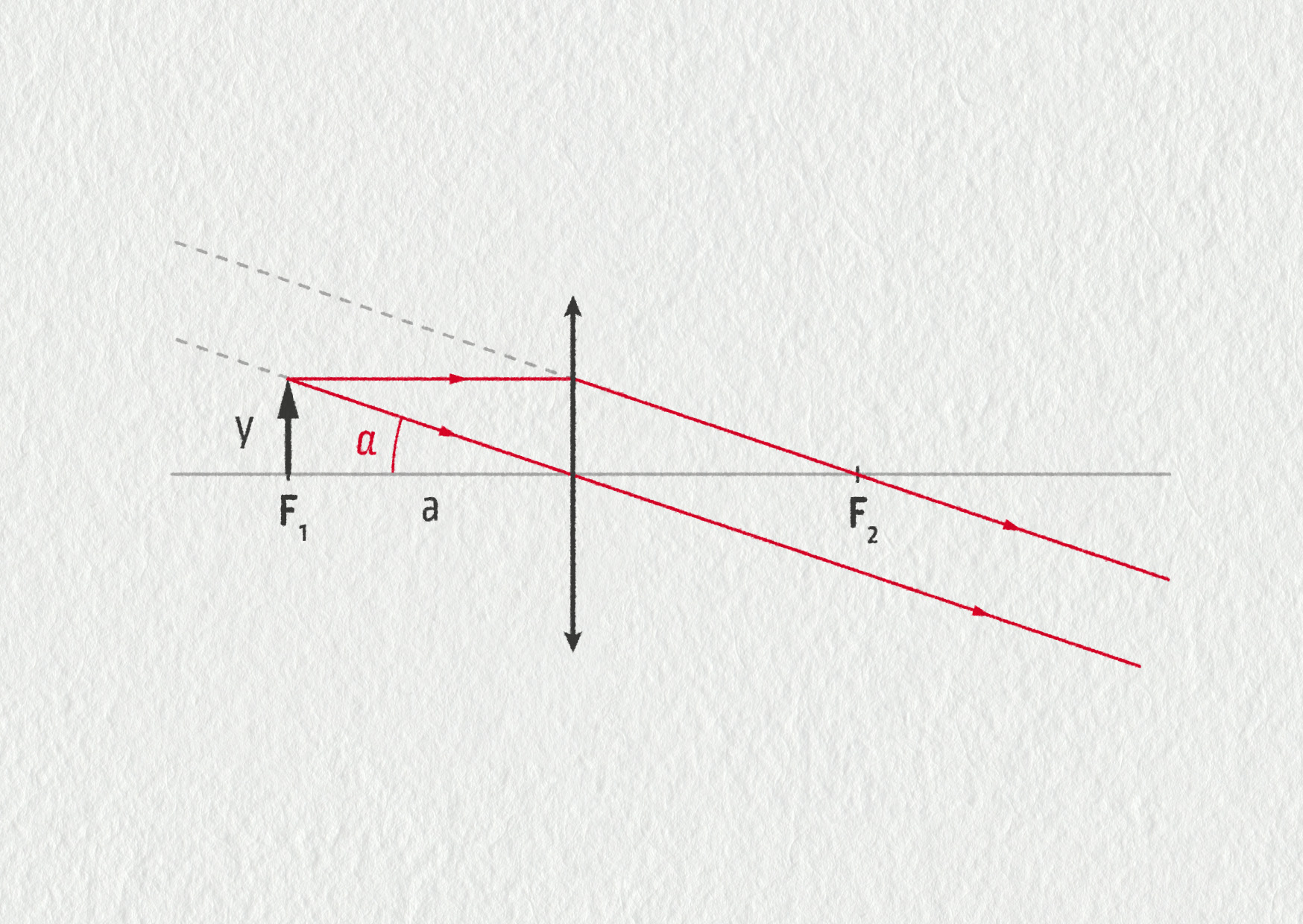
Zdroj
b) Zorný úhel je v náčrtku označen jako \(\alpha\). Z pravoúhlého trojúhelníku vyplývá, že
\[ \tan\alpha = \frac ya = \frac yf = \frac{4}{50} = 0{,}08\;. \]Odtud \(\alpha=4{,}6^\circ\).
c) Zorný úhel při pozorování okem označíme \(\beta\). Platí
\[ \tan\beta = \frac yd = \frac{4}{250} = 0{,}016\;. \]Odtud \(\beta=0{,}9^\circ\).
d) Úhlové zvětšení lupy je poměr zorných úhlů: \(\gamma=\alpha/\beta=5\).
e) Pro úhlové zvětšení platí \(\gamma=\alpha/\beta\). Pro malé úhly můžeme použít přibližný vztah \(\alpha/\beta\approx\tan\alpha/\tan\beta\). Pak už stačí dosadit:
\[ \gamma = \frac{\alpha}{\beta} \approx \frac{\tan\alpha}{\tan\beta} = \frac{y/f}{y/d} = \frac yd\; \]V příkladu jsme dokázali, že úhlové zvětšení lupy (s předmětem v ohnisku) můžeme určit jako \(\gamma=d/f\), kde \(d\) je konvenční zraková vzdálenost a \(f\) je ohnisková délka použité čočky. Ale toto úhlové zvětšení je omezeno tím, že ohniskovou délku čočky nelze zmenšovat libovolně. Čím silnější je čočka, tím větší problém představují její optické vady. Naštěstí můžeme použít dvě nebo více čoček a vytvořit tak mikroskop.
Mikroskop
Základní schéma mikroskopu vidíme na obrázku. Spojku s menší ohniskovou vzdáleností, která je blízko pozorovanému předmětu y, označujeme jako objektiv. Objektiv vytváří skutečný, převrácený a zvětšený obraz \(y'\). Ten vzniká záměrně v blízkosti ohniska druhé spojky s větší ohniskovou vzdáleností, kterou označujeme jako okulár. Okulár vytváří neskutečný, zvětšený a přímý obraz \(y''\), který pozorujeme okem.
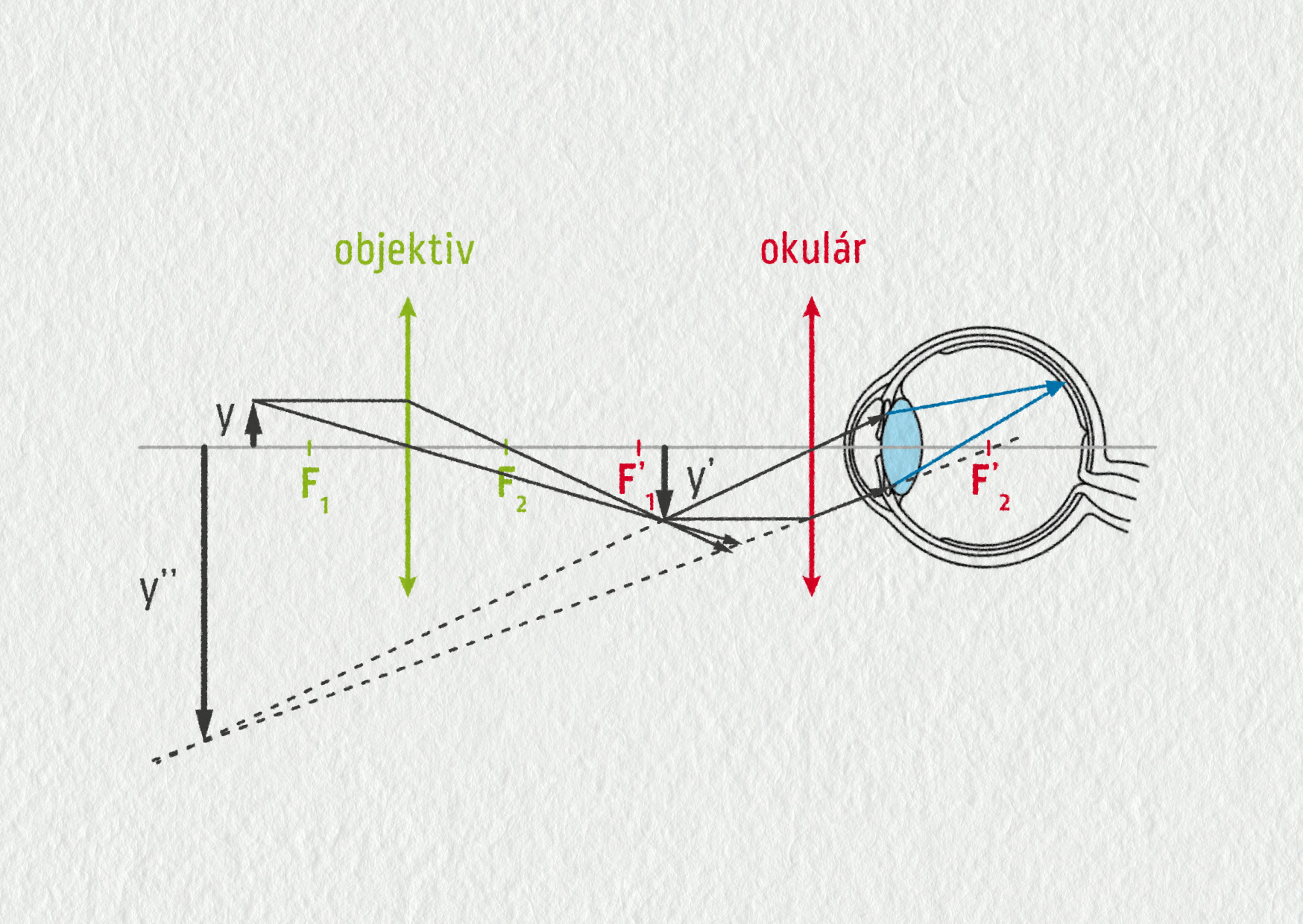
Zdroj
Pro úhlové zvětšení mikroskopu můžeme odvodit vztah:
\[ \gamma = \frac{\Delta}{f_\mathrm{OB}} \frac{d}{f_\mathrm{OK}}\;, \]kde \(\Delta=|F_2F_{1'}|\) je vzdálenost ohnisek objektivu a okuláru, \(f_\mathrm{OB}\) je ohnisková délka objektivu, \(f_\mathrm{OK}\) je ohnisková délka okuláru a \(d=25\ \mathrm{cm}\) je konvenční zraková vzdálenost.

Zdroj
Úhlové zvětšení optického mikroskopu je v praxi omezeno hodnotou cca 1 000. Tento limit nevyplývá ze vztahu pro zvětšení, je totiž způsoben vlnovými vlastnostmi světla.
Keplerův dalekohled
Pomocí dvou spojek můžeme vytvořit také určitý druh dalekohledu, který se po svém objeviteli nazývá Keplerův. Jeho schéma vidíme na obrázku 23.65. Pozorovaný předmět se nachází v nekonečnu a bez dalekohledu bychom jej pozorovali pod úhlem \(\alpha\). Objektiv (první spojka) vytváří skutečný, převrácený a zmenšený obraz \(y'\). Okulár (druhá spojka) pak slouží jako lupa. Vytváří neskutečný obraz \(y''\) v nekonečnu, který pozorujeme okem.
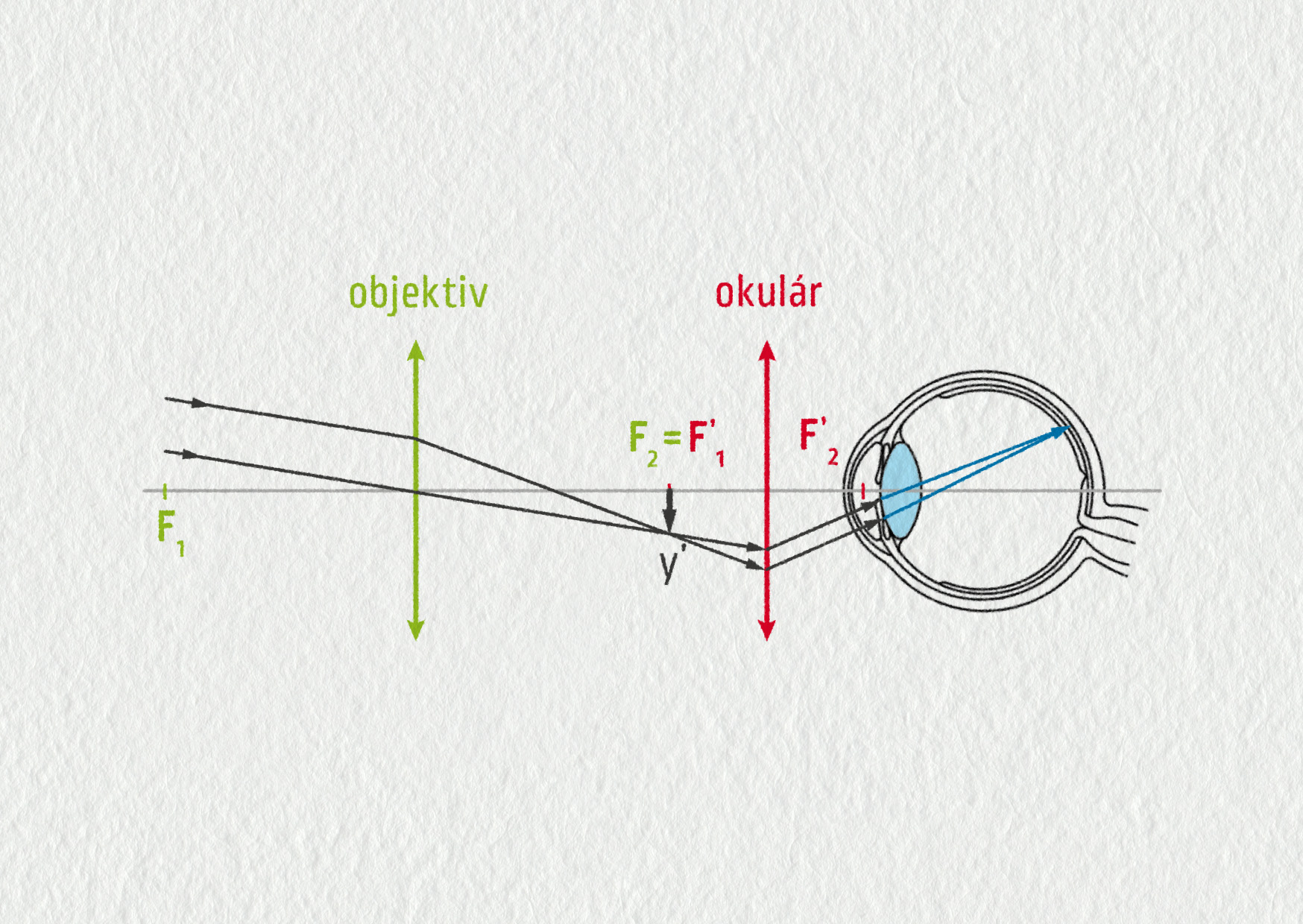
Zdroj
Pro úhlové zvětšení Keplerova dalekohledu platí:
\[ \gamma = \frac{f_\mathrm{OB}}{f_\mathrm{OK}}\;, \]kde \(f_\mathrm{OB}\) je ohnisková délka objektivu a \(f_\mathrm{OK}\) je ohnisková délka okuláru.
Keplerovým dalekohledem vidíme sledovaný objekt převrácený, což v astronomii nevadí. Pro pozemská pozorování bývá chod paprsků v dalekohledu upraven pomocí hranolů tak, aby výsledný obraz nebyl převrácený. Takto upravený dalekohled se nazývá triedr. Rozlišovací schopnost dalekohledu je limitována vlnovými vlastnostmi světla, podobně jako u mikroskopu. Kromě samotného zvětšení má zásadní význam také průměr objektivu. Podrobněji o tom pojednává článek v kapitole 24. V astronomii se dnes už Keplerova konstrukce dalekohledu příliš nepoužívá. Většinou se setkáme se zrcadlovými dalekohledy, neboť zrcadla je možné vyrobit větší a netrpí barevnou vadou.

Zdroj

