Světlo je jeden z nejzajímavějších fyzikálních objektů. Spory o podstatu světla provázely fyziku po velkou část její historie. Otázku, „co“ je to světlo, však nechejme do dalších kapitol. V geometrické optice se zabýváme otázkou, „jak“ se světlo šíří prostorem. Pomocí geometrické optiky můžeme pochopit, jak funguje zrak a umožňuje nám konstruovat optické přístroje od brýlí po fotoaparáty a dalekohledy.
Proč vidíme?
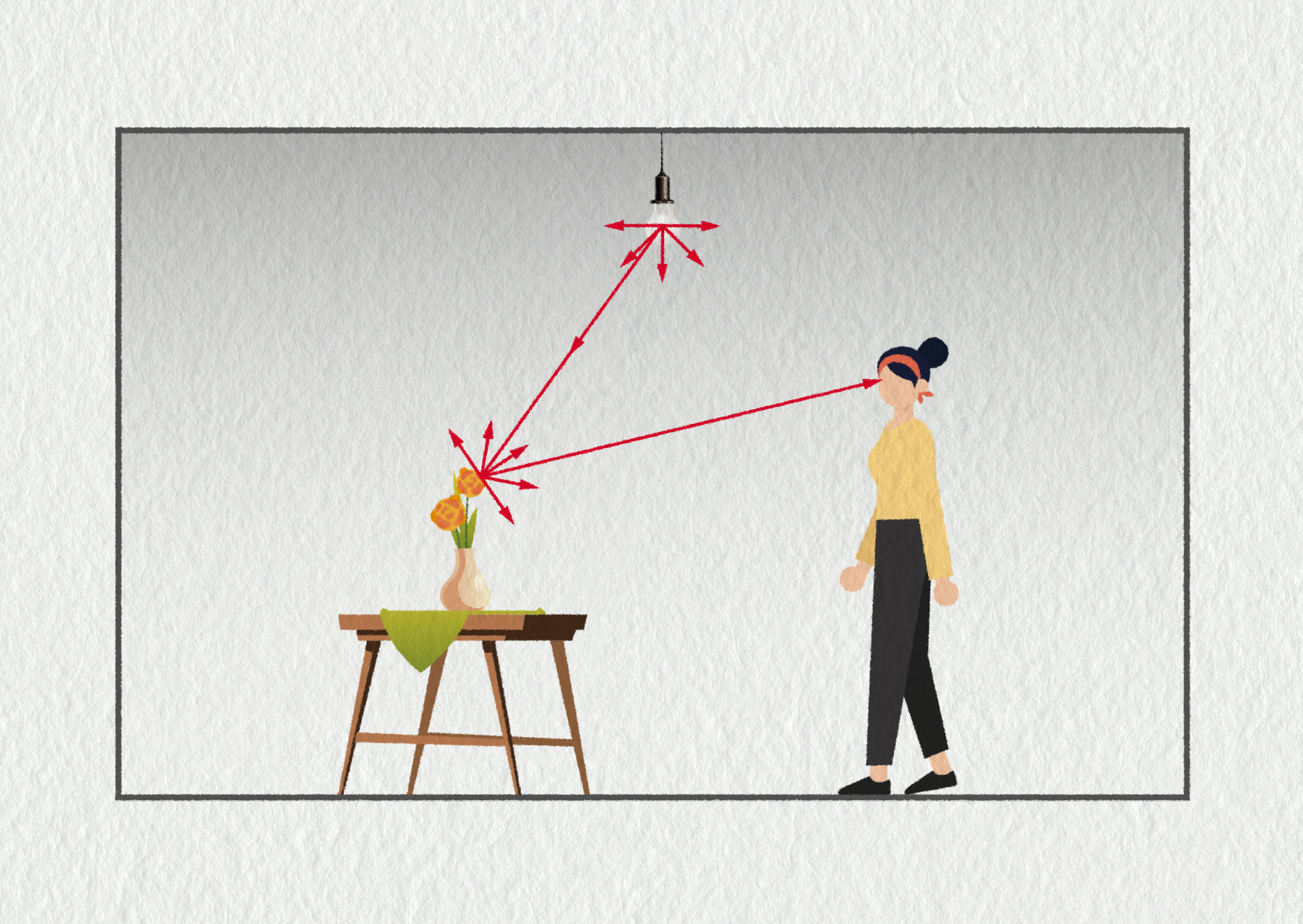
Na úvod si představíme základní pojmy geometrické optiky. Použijeme k tomu příklad Hanky sledující květinu (viz obrázek 23.15). Jaké jsou podmínky nutné k tomu, aby lidské oko mohlo vidět nějaký předmět?
Zdroj
Zdroj světla
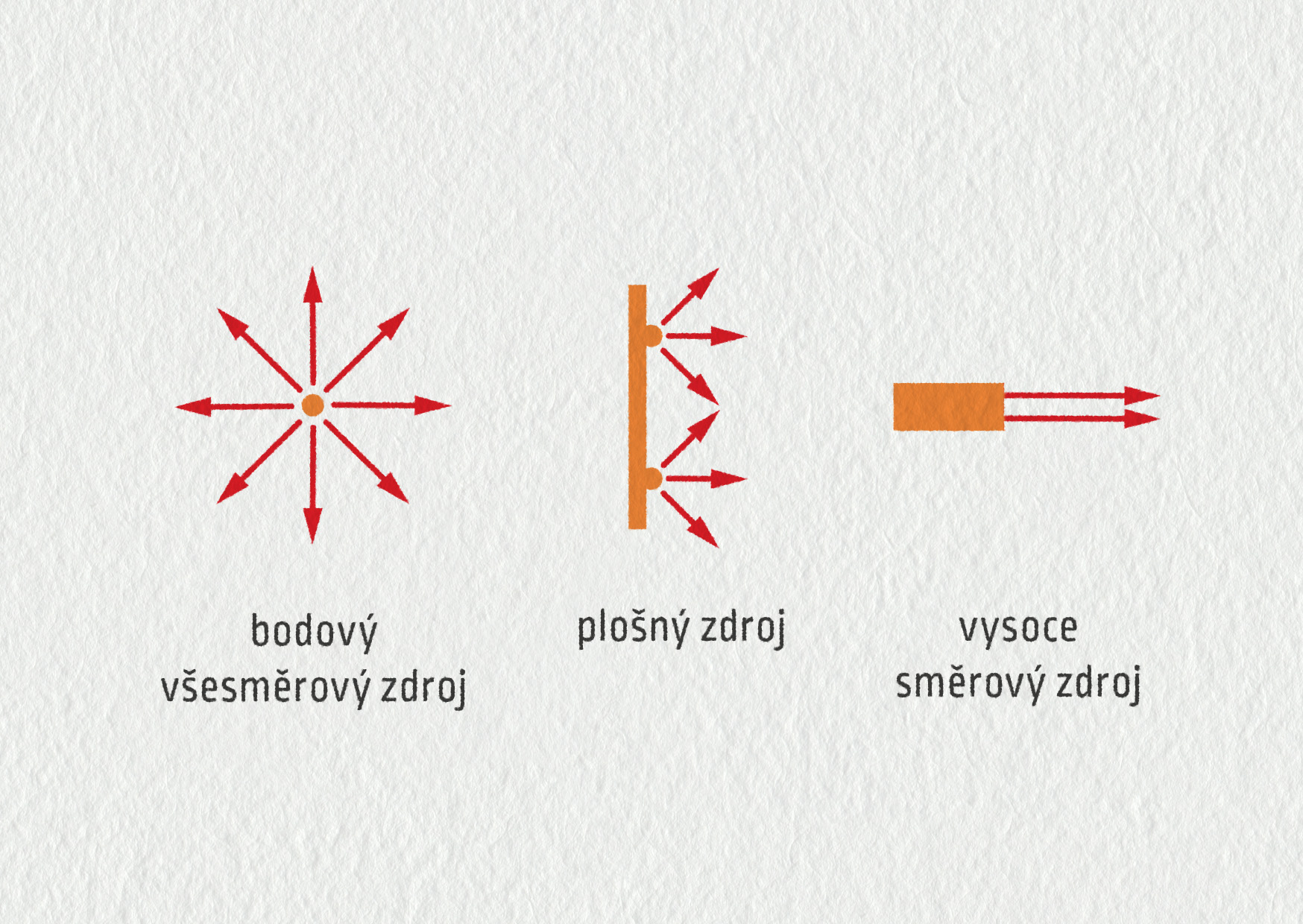
Zdrojem světla je předmět, ze kterého vychází světlo (Slunce, žárovka, plamen, světluška). O zdrojích světla se podrobněji dočtete v kapitole 26. Pro účely geometrické optiky je podstatná velikost zdroje a to, jakými směry se z něj šíří světlo. Nejjednodušším případem je bodový všesměrový zdroj (viz obrázek 23.16). Je to bod, ze kterého vychází světlo všemi směry. Takový zdroj ve skutečnosti neexistuje, ale například hvězdy na noční obloze mají k tomuto ideálu velmi blízko. Většina zdrojů kolem nás jsou zdroje plošné. Ty se skládají z velkého množství mnoha bodových zdrojů (například zářivka). Možná vás napadlo, že zářivka je mnohem menší než hvězda, kterou jsme použili jako příklad bodového zdroje. Ano, ale hvězda je od nás, na rozdíl od zářivky, velmi daleko. Dalo by se říci, že každý plošný zdroj, pozorovaný z velké vzdálenosti, se bude jevit jako bodový. Posledním příkladem je směrový zdroj. Například laserové ukazovátko je plošným zdrojem, ale světlo z něj vychází prakticky jen jedním směrem.
Zdroj
Prostředí
Abychom mohli vidět, musíme se nacházet ve vhodném prostředí, které světlo příliš nepohlcuje. Takové prostředí označujeme jako průhledné a jeho ideálním případem je vakuum. Všechna ostatní průhledná prostředí (voda, vzduch, sklo) světlo do určité míry ovlivňují. Mohou ho pohlcovat nebo rozptylovat. Pohlcování světla je dobře pozorovatelné v případě mořské vody – do větších hloubek se žádné světlo nedostane. Pohlcování světla je často selektivní – různé barvy jsou pohlcovány různě. U vody je nejvíce pohlcována červená barva, do hloubky proto proniká jen modrá. Při rozptylu je světlo náhodně vychylováno ze svého původního směru. Rozptyl většinou nastává na mnoha mikroskopických částečkách (například prachových částicích ve vzduchu).

Zdroj
Předmět
U neprůhledných pozorovaných předmětů záleží na jejich povrchu, kolik světla pohltí a kolik odrazí, případně jakým směrem. Pohlcování světla je opět selektivní – některé barvy jsou pohlcovány, jiné nikoliv. Tím získávají předměty svoji barvu (více o barevném vidění v kapitole 24). Až na zvláštní výjimky, odrážejí předměty světlo do všech směrů.
Máme tu zdroj světla, průhledné prostředí, kterým se světlo šíří, a předměty, od kterých se odráží. Nakonec musí světlo dopadnout do zobrazovacího zařízení, kde se z dopadajícího světla vytváří obraz. Obraz umí vytvářet nejen lidské oko ale také fotoaparát nebo kamera. Jejich princip vyložíme na konci této kapitoly.
Zákon přímočarého šíření světla
Geometrická optika získala svůj název zcela záměrně. Šíření světla totiž popisuje pomocí geometrie. Konkrétně k tomu využívá paprsky. Paprsky jsou myšlené čáry, které popisují dráhu šíření světla prostředím. V částicovém modelu by se jednalo o trajektorie světelných částic a ve vlnovém modelu o kolmice na vlnoplochy. Celá geometrická optika stojí na třech základních zákonech, které popisují chod paprsků v různých situacích. Tyto tři zákony je možné odvodit z Fermatova principu (viz motivační aktivita) nebo pomocí vlnové teorie (viz kapitola 22).
První zákon popisuje, jak se světlo šíří v homogenním průhledném prostředí. To je takové prostředí, které má ve všech bodech stejné vlastnosti.
V homogenním průhledném prostředí se světlo šíří po přímkách.
K vyřešení úlohy, která se odehrává v homogenním prostředí, vám proto bude stačit jen pravítko.
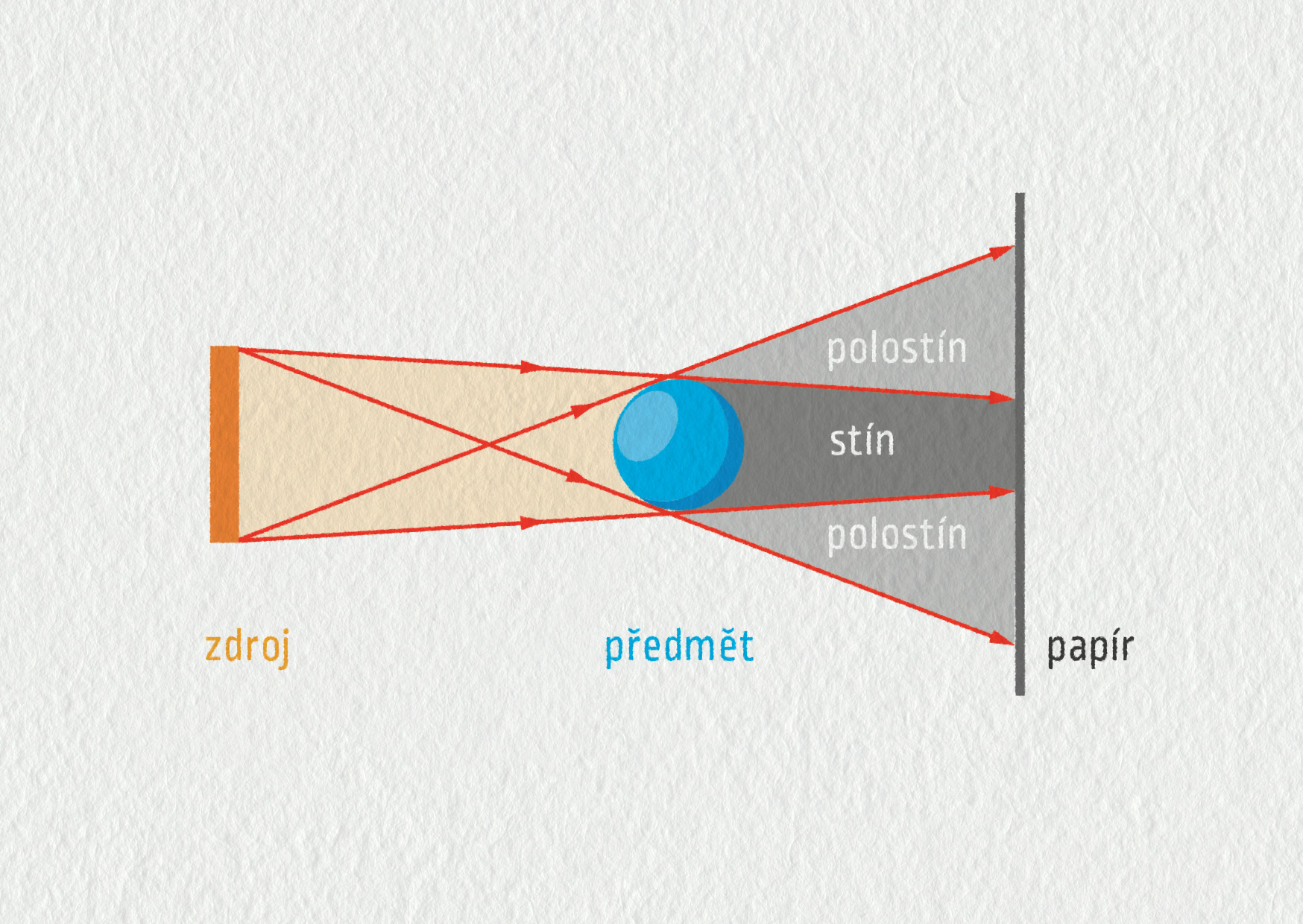
Pomocí paprsků odvoďte, jak bude vypadat stín kruhového předmětu osvětleného plošným zdrojem světla. Úlohu řešte pouze dvourozměrně. Trojrozměrné řešení můžete zkusit vyřešit na základě své prostorové představivosti nebo pomocí experimentu v tmavé místnosti.

Zdroj
Z každého bodu plošného zdroje vychází do všech směrů nekonečno přímých paprsků. V geometrické optice si z nich vždy vybíráme jen ty, které jsou podstatné pro řešení úlohy. V tomto případě to budou „okrajové“ paprsky, které tvoří tečny k předmětu z krajních bodů zdroje (viz obrázek 23.19a).
Zdroj

Zdroj
Zákon odrazu
Nyní se zaměříme na situaci, kdy světlo dopadá na rozhraní dvou různých prostředí. V tomto případě mohou nastat dva jevy – odraz a lom. Zatímco lom světla nastává pouze na rozhraní dvou průhledných prostředí, k odrazu dochází prakticky od všech povrchů. Ke studiu zákona odrazu však budeme potřebovat předmět s dostatečně hladkým povrchem, a tím je zrcadlo. Na obrázku je zachycen odraz laserového světla od rovinného zrcadla. Pomocí úhloměru na pozadí můžeme jednoduše vidět, že úhel dopadu \(\alpha\) je stejný jako úhel odrazu \(\alpha'\).

Zdroj
Pro pořádek je potřeba úhel dopadu a odrazu správně definovat. Úhly v optice měříme vždy od kolmice dopadu, což je kolmice na rozhraní v bodě dopadu (viz obrázek 23.20). Dále je potřeba doplnit, že odražený paprsek leží ve stejné rovině dané kolmicí dopadu a dopadajícím paprskem. Zákon odrazu můžeme zapsat matematicky velmi jednoduše:
Zákon odrazu:
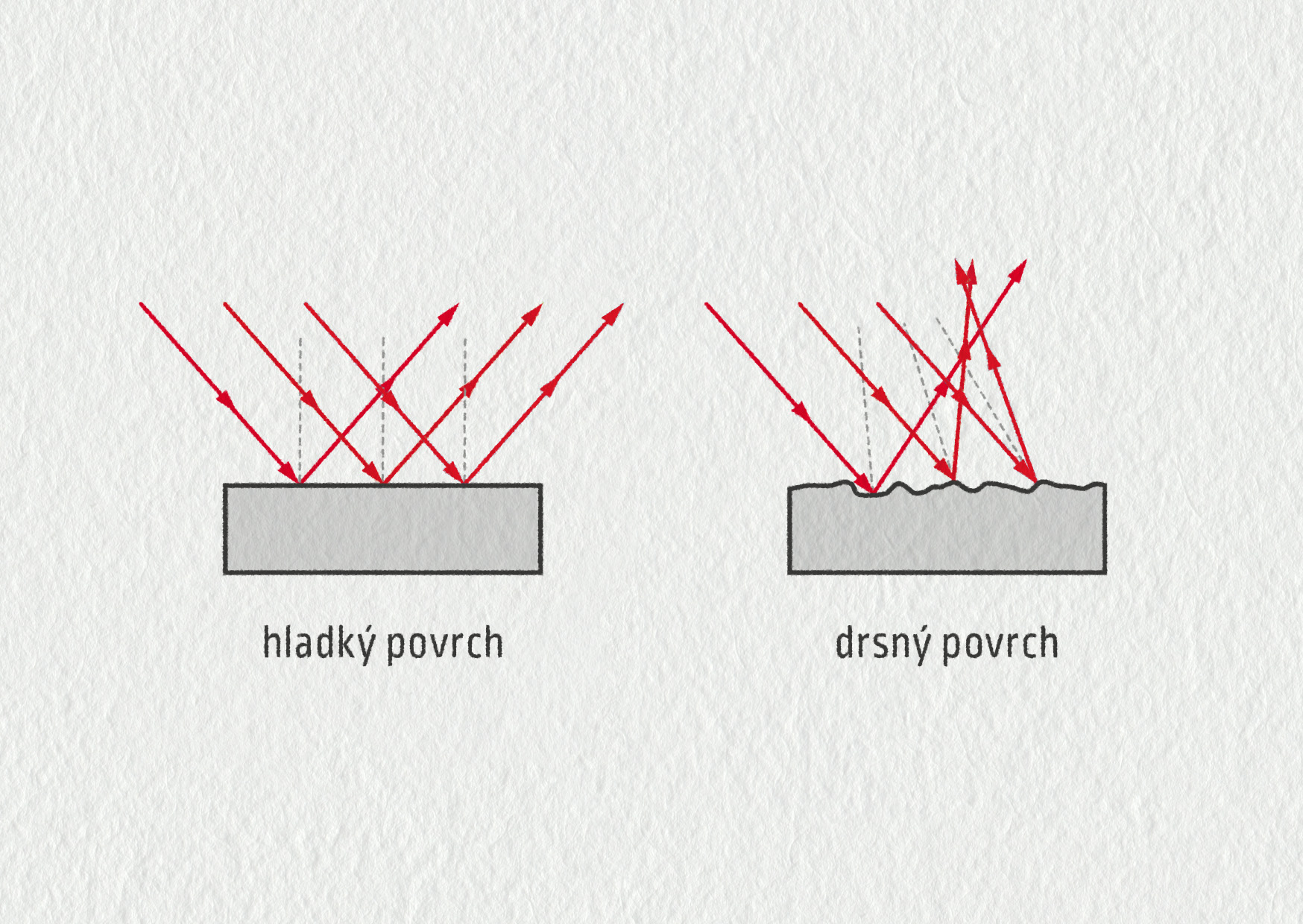
\[ \alpha=\alpha' \]Aby se světlo skutečně odrazilo přesně podle zákona odrazu, musí být odrazná plocha dostatečně hladká na mikroskopické úrovni. Dostatečně hladké rozhraní pro odraz vytváří například klidná vodní hladina nebo sklo. Právě ze skla se vyrábí také zrcadla, a to nanesením tenké kovové vrstvy na zadní stranu skla.
Co se stane, pokud se světlo odráží od drsného povrchu, ukazuje další obrázek 23.21. Odražené světlo je rozptýlené do mnoha směrů. Tento druh odrazu je v praxi mnohem častější, protože většina materiálů má na mikroskopické úrovni drsný povrch. Díky rozptylu se vždy najdou nějaké paprsky, které zamíří i do oka pozorovatele – předmět je pro něj viditelný i ze směru, který neodpovídá úhlu odrazu. Proto přečtete třeba text napsaný na tabuli z jakéhokoliv místa ve třídě.
Zdroj
Jak vysoké rovné zrcadlo a v jaké výšce potřebuje stojící člověk vysoký 180 cm k tomu, aby se v něm viděl celý (tedy od chodidel po temeno hlavy)? Zrcadlo je umístěno na svislé stěně. K vyřešení úlohy použijte geometrickou konstrukci.
Situace je znázorněna na obrázku. Nejdřív je potřeba si uvědomit, že je úplně jedno, jak daleko od zrcadla člověk stojí. Z obrázku vyplývá, že bude stačit zrcadlo o výšce 90 cm umístěné zhruba naproti horní polovině těla. Přesná poloha zrcadla závisí na poloze očí pozorovatele.
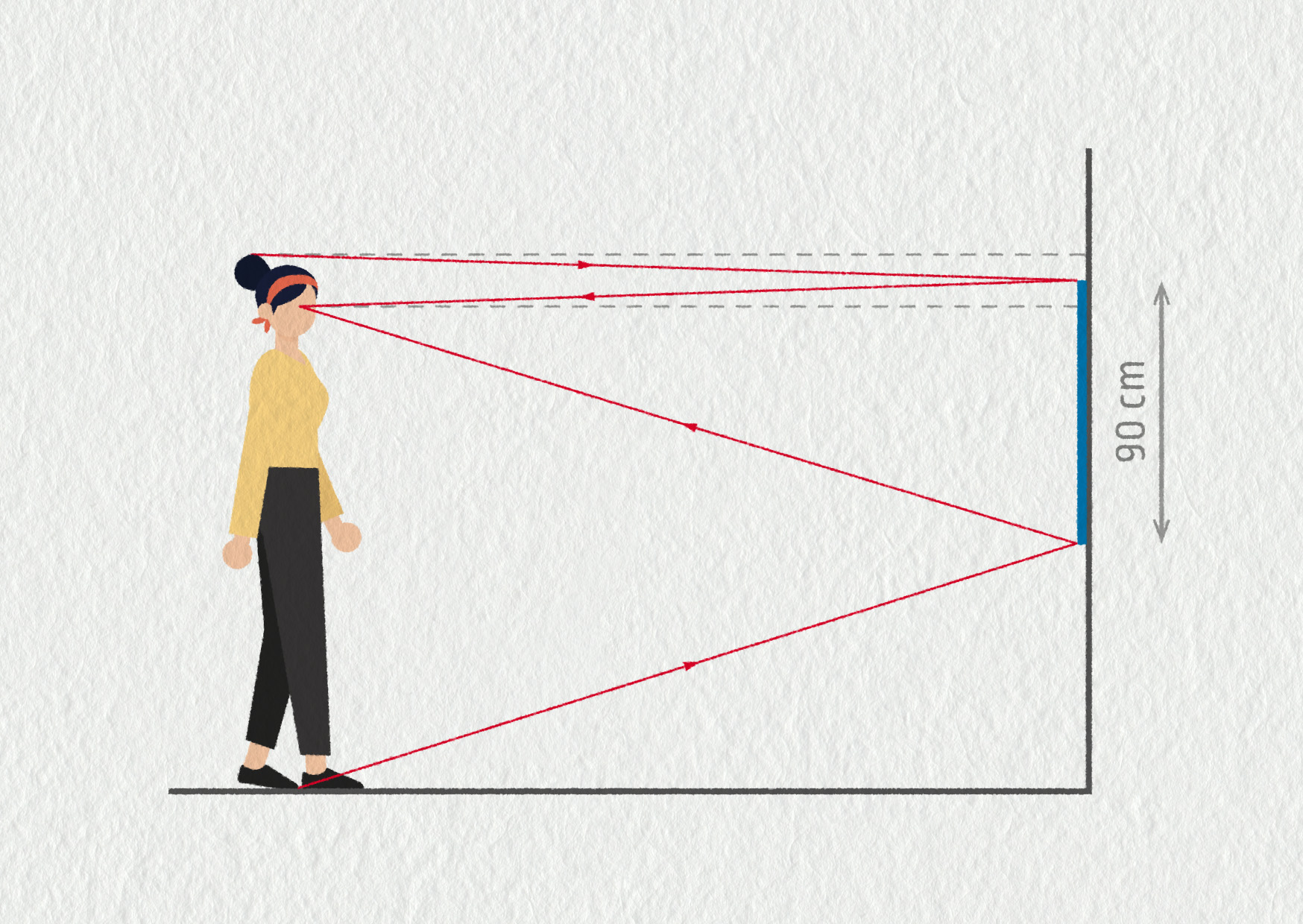
Zdroj
Zákon lomu
Než si představíme zákon lomu, je potřeba zavést jednu praktickou veličinu, která charakterizuje dané optické prostředí. Jedná se o index lomu \(n\). Je definován jako podíl rychlosti světla ve vakuu a rychlosti světla v daném prostředí.
Index lomu
\[ n = \frac cv \]\(c=299\,792\,458\ \mathrm{m/s} \mathrel{\approx} 3\cdot10^8\ \mathrm{m/s}\) – rychlost světla ve vakuu
\(v\) – rychlost světla v daném prostředí
Jinými slovy, index lomu je bezrozměrná veličina, která určuje, kolikrát je rychlost světla v daném prostředí menší než ve vakuu. Hodnoty indexu lomu pro některá prostředí jsou uvedeny v tabulce. Jak vidíte, indexy lomu jsou docela pěkná čísla blízká jedničce, narozdíl od rychlosti světla.
| prostředí | index lomu |
|---|---|
| vakuum | 1 |
| vzduch | 1,0003 |
| voda (při 20 °C) | 1,33 |
| slaná voda (26%) | 1,37 |
| sladká voda (50%) | 1,42 |
| etanol | 1,36 |
| křemenné sklo | 1,46 |
| sklo (podle druhu) | 1,5–1,9 |
| diamant | 2,42 |
| karbid křemíku (SiC) | 2,65 |
Poznámka k tabulce: index lomu mírně závisí také na vlnové délce světla, uvedené hodnoty jsou pro vlnovou délku 580 nm (odpovídá žluté barvě).
Zákon lomu popisuje situaci, kdy se paprsek po dopadu na rozhraní láme – proniká do druhého prostředí. Celá situace je názorně zachycena na obrázku 23.23 zobrazujícím lom laserového světla při přechodu ze vzduchu do plastu.

Zdroj
Zákon lomu
Jestliže se paprsek šíří v prostředí o indexu lomu \(n_1\) a dopadá na rozhraní pod úhlem \(\alpha\), tak se ve druhém prostředí o indexu lomu \(n_2\) láme pod úhlem \(\beta\), přičemž platí
\[ n_1\sin\alpha = n_2\sin\beta \]Mohou nastat dvě různé situace – lom ke kolmici a lom od kolmice. Lom ke kolmici nastane v případě, že se světlo šíří do prostředí s vyšším indexem lomu (například ze vzduchu do plexiskla). Druhá varianta, tedy lom od kolmice, nastane, když se paprsek šíří do prostředí s nižším indexem lomu (například z plexiskla do vzduchu). Obě situace můžete porovnat také na obrázku 2.34.

Zdroj
Na předchozím obrázku 23.24 si můžeme všimnout také odraženého paprsku. Je to tím, že odraz a lom probíhají většinou současně – část světla se odrazí a zbytek se zlomí.
Pomocí obrázků lomu světla určete index lomu plexiskla, ze kterého je vyroben půlválec. Proveďte výpočet pro obě situace (lom ke kolmici a lom od kolmice)
Z obrázku odečteme úhel dopadu \(\alpha=30^\circ\). Úhel lomu je v případě lomu ke kolmici \(\beta=20^\circ\). V případě lomu od kolmice \(\beta=47^\circ\). Nyní zapíšeme zákon lomu
\[ n_1\sin\alpha = n_2\sin\beta \]V prvním případě vstupuje světlo ze vzduchu do plexiskla a platí tedy \(n_1=1\) (vzduch) a \(n_2\) je hledaný index lomu plexiskla:
\[ \sin\alpha = n_2\sin\beta\;. \]Odtud
\[ n_2 = \frac{\sin\alpha}{\sin\beta}\;. \]Po dosazení číselných hodnot odečtených z obrázku vyjde pro index lomu plexiskla \(n_2=1{,}46\).
V druhém případě vstupuje světlo z plexiskla do vzduchu a platí tedy \(n_2=1\) a \(n_1\) je hledaný index lomu plexiskla:
\[ n_1\sin\alpha = \sin\beta\;. \]Odtud
\[ n_1 = \frac{\sin\beta}{\sin\alpha}\;. \]Po dosazení číselných hodnot odečtených z obrázku vyjde pro index lomu plexiskla \(n_2=1{,}46\).
Světelný paprsek dopadá na skleněnou desku s rovnoběžnými stěnami (viz obrázek). Načrtněte průchod paprsku deskou. Pomocí zákona lomu dokažte, že paprsek vycházející z desky je rovnoběžný s dopadajícím paprskem.

Zdroj
Řešení je patrné z obrázku 23.26. Úhel lomu z prvního rozhraní (\(\beta\)) je stejně velký jako úhel dopadu na druhé rozhraní (\(\beta'=\beta\)). Zákon lomu pro první rozhraní zapíšeme jako \(n_1\sin\alpha=n_2\sin\beta\) (\(n_1\) je index lomu vzduchu, \(n_2\) je index lomu skla). Pro druhé rozhraní platí \(n_2\sin\beta=n_1\sin\alpha'\). Porovnáním obou rovnic dostaneme \(n_1\sin\alpha=n_1\sin\alpha'\) a odtud \(\alpha=\alpha'\). Proto je paprsek po průchodu deskou rovnoběžný s dopadajícím paprskem.
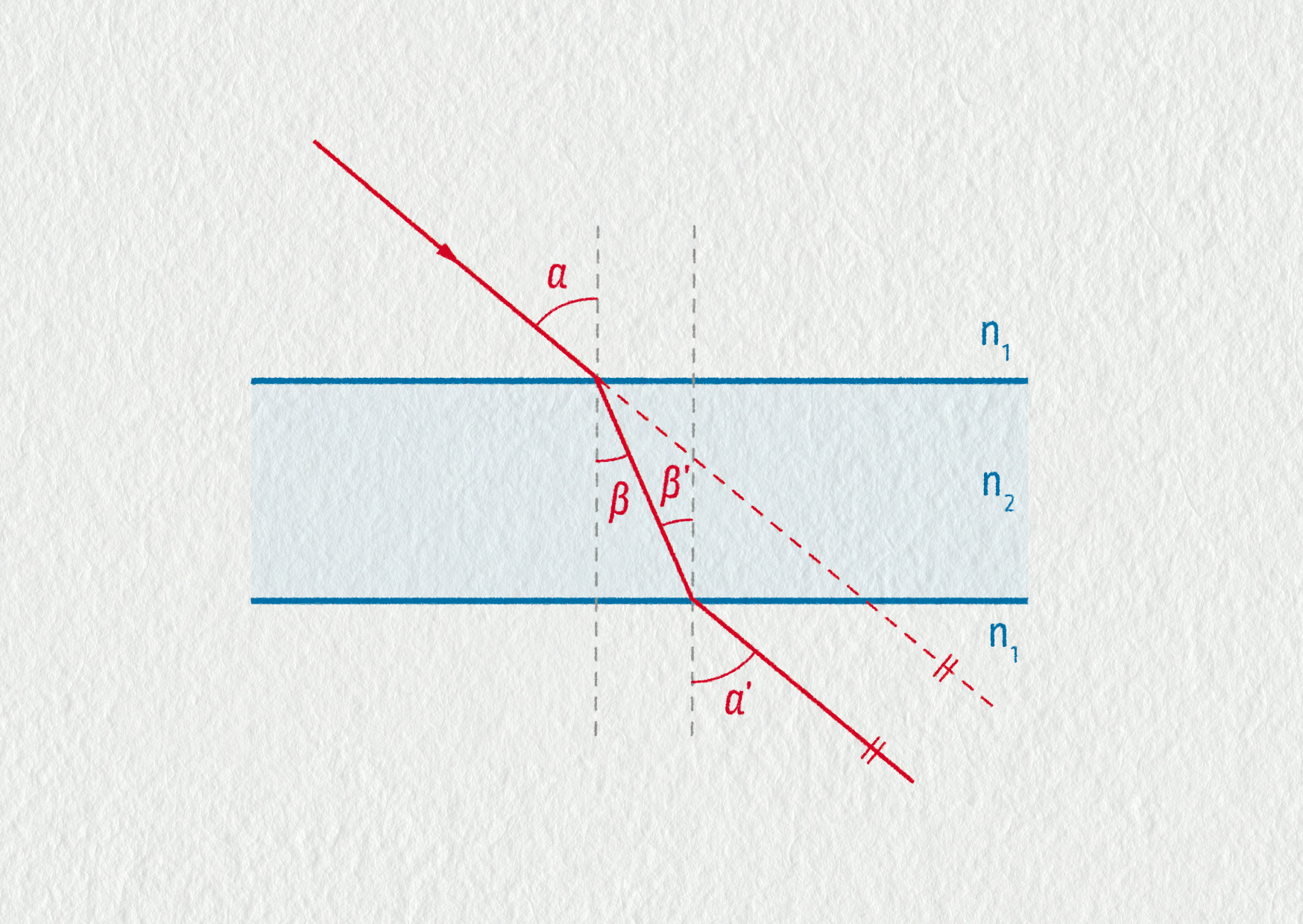
Zdroj
V případě lomu od kolmice, kdy se paprsek šíří z prostředí s větším indexem lomu \(n_1\) do prostředí s nižším indexem lomu \(n_2\), může nastat zajímavý jev, který se nazývá totální odraz. Na sérii obrázků 2.37 je zachycena situace, kdy postupně zvětšujeme úhel dopadu \(\alpha\). Až do chvíle, kdy úhel lomu \(\beta\) dosáhne hodnoty téměř 90°, můžeme pozorovat odražený i lomený paprsek. Budeme-li dále zvětšovat úhel dopadu, lomený paprsek zcela zmizí a veškeré světlo se od rozhraní odrazí.

Zdroj
Pro mezní situaci, kdy \(\beta=90^\circ\), definujeme mezní úhel dopadu \(\alpha_\mathrm{m}\), po jehož překročení již nemůže nastat lom a proto se veškeré světlo od rozhraní odrazí. Mezní úhel lze určit jednoduše ze zákona lomu, do kterého dosadíme \(\alpha=\alpha_\mathrm{m}\) a \(\beta=90^\circ\):
\[\begin{aligned} n_1\sin\alpha_\mathrm{m} &= n_2\sin 90^\circ\\ n_1\sin\alpha_\mathrm{m} &= n_2\cdot1\\ \sin\alpha_\mathrm{m} &= n_2/n_1\\ \end{aligned}\]Výše uvedený vztah pro mezní úhel platí za podmínky, že \(n_1>n_2\). Je-li druhým prostředím vzduch, tak lze vztah ještě zjednodušit, jelikož přibližně platí \(n_2=1\).
Na obrázku 23.28 vidíme dvojitý totální odraz světla v hranolu ve tvaru rovnoramenného trojúhelníku. Hranol tohoto tvaru se používá k převrácení obrazu. Stanovte podmínku pro index lomu materiálu, ze kterého je hranol vyroben, aby dopadající a odražený paprsek byly rovnoběžné.

Zdroj
Z obrázku 23.28 je patrné, že světlo uvnitř hranolu dopadá na rozhraní pod úhlem \(\alpha=45^\circ\). Pro mezní úhel platí rovnice:
\[ n_1\sin\alpha_\mathrm{m} = n_2\sin(90^\circ)\;. \]Světlo se šíří do vzduchu, proto \(n_2=1\). Odtud
\[ n_1 = 1/\sin\alpha_\mathrm{m}\; \]Mezní úhel musí být menší nebo roven 45°. Dostaneme \(n_1=1/\sin(45^\circ)=1{,}41\). Závěr: index lomu materiálu hranolu musí mít hodnotu alespoň 1,41.
Totální odraz světla má bohaté využití v praxi. Kromě odrazných hranolů se využívá hlavně v optických vláknech. Princip šíření světla v optickém vláknu ukazuje obrázek.

Zdroj
Ohebné a tenké vlákno umožňuje šíření světla jen s minimálními ztrátami. Využití najdeme v optoelektronice a telekomunikaci, kde slouží k přenosu signálů. V medicíně se optická vlákna využívají v endoskopu, který slouží k vyšetření dutin v lidském těle.
Odraz a lom světla

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

