Deformace gumy
Úkol: Studujte prodlužování gumového vlákna při rostoucím zatížení.
- Sestrojte graf závislosti normálového napětí \(\sigma\) na relativním prodloužení \(\varepsilon\).
- Z grafu odečtěte hodnotu meze pružnosti \(\sigma_B\) a hodnotu Youngova modulu \(E\).
- Výsledky porovnejte s různými tabulkovými materiály.
- Odpovídají vlastnosti materiálu jeho charakteristikám z grafu na obrázku 13.66?
Vybavení: gumové vlákno 1 mm × 3 mm, stojan, sada závaží, pravítko, posuvné délkové měřidlo
Teoretický úvod
Zdroj
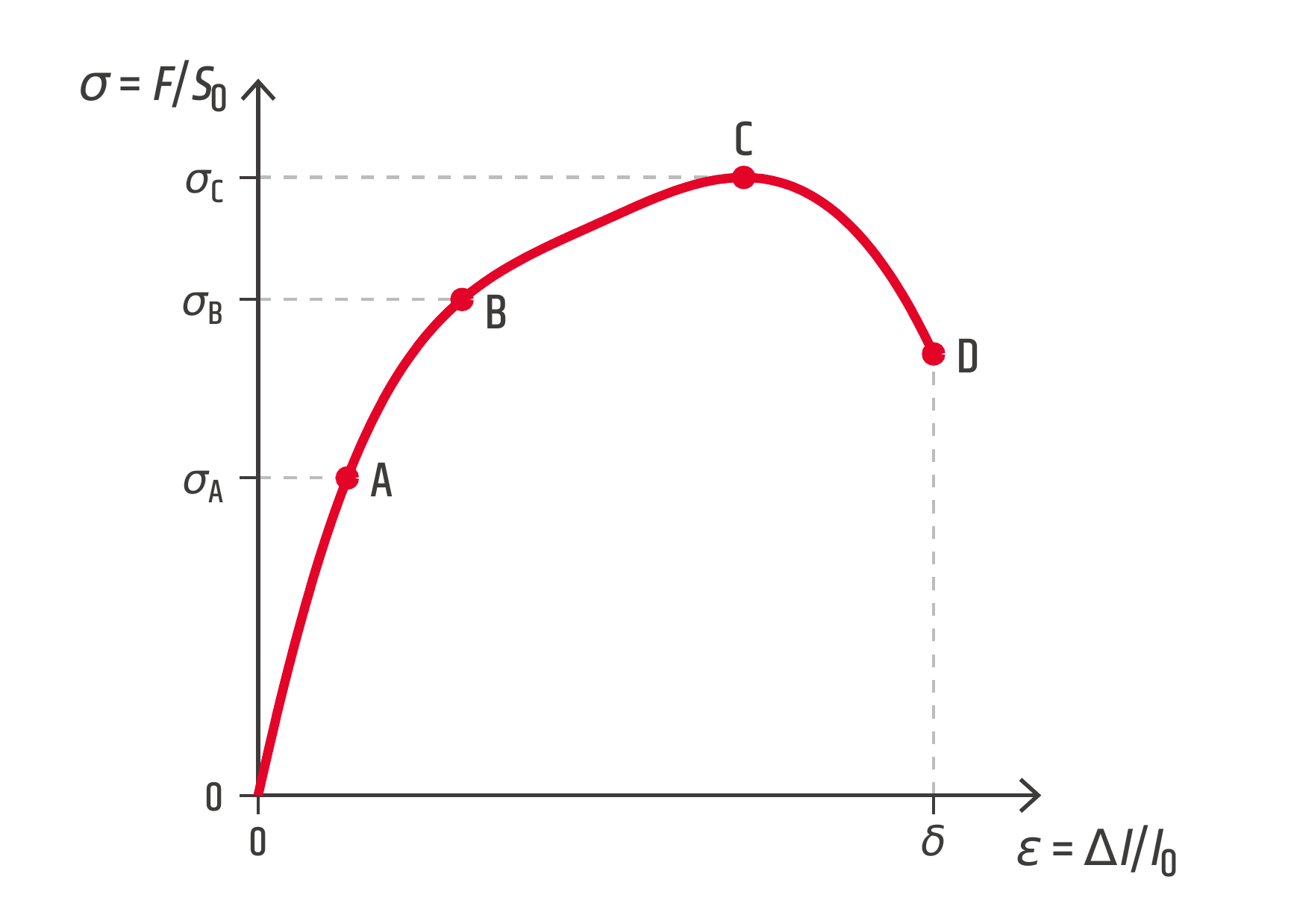
Na vloženém obrázku si objasněme důležité body deformační křivky. Část OA této křivky je lineární, zde platí Hookův zákon. Napětí \(\sigma_A\) odpovídající bodu A označuje mez úměrnosti. Youngův modul pružnosti \(E\) je roven směrnici této lineární části grafu. Bod B odpovídá mezi pružnosti. Naší zkouškou se budeme snažit určit mez, po kterou je materiál stále pružný, což znamená, že přestane-li působit deformační síla, vrátí se ke své původní délce.
Vrchol deformační křivky odpovídá mezi pevnosti, tedy maximálnímu napětí dosaženému při tahové zkoušce. V bodě D dochází k přetržení materiálu. Tyto dvě charakteristiky studovat nebudeme.

Zdroj
Postup:
- Připravte si kousek gumy dlouhý přibližně 35 cm. Na obou jeho koncích vytvořte očka tak, aby mezi uzlíky zůstalo alespoň 5 cm. Tuto délku budeme považovat za délku gumy v nezatíženém stavu a značit ji \(l_0\). Změřte příčný průřez gumy.
- Gumu zavěste na stojan a postupně na ni zavěšujte závaží o hmotnosti 50 g. Změřte její délku \(l\).
- Odeberte všechna závaží a změřte délku gumy v nezatíženém stavu.
- Postup opakujte do doby, kdy se guma již nevrátí do své původní délky.
- Vypočítejte relativní prodloužení \(\varepsilon\) a napětí \(\sigma \textsubscript{n} \).
- Sestrojte graf napětí na relativním prodloužení a odpovězte na otázky v zadání.
Ukázka výsledků:
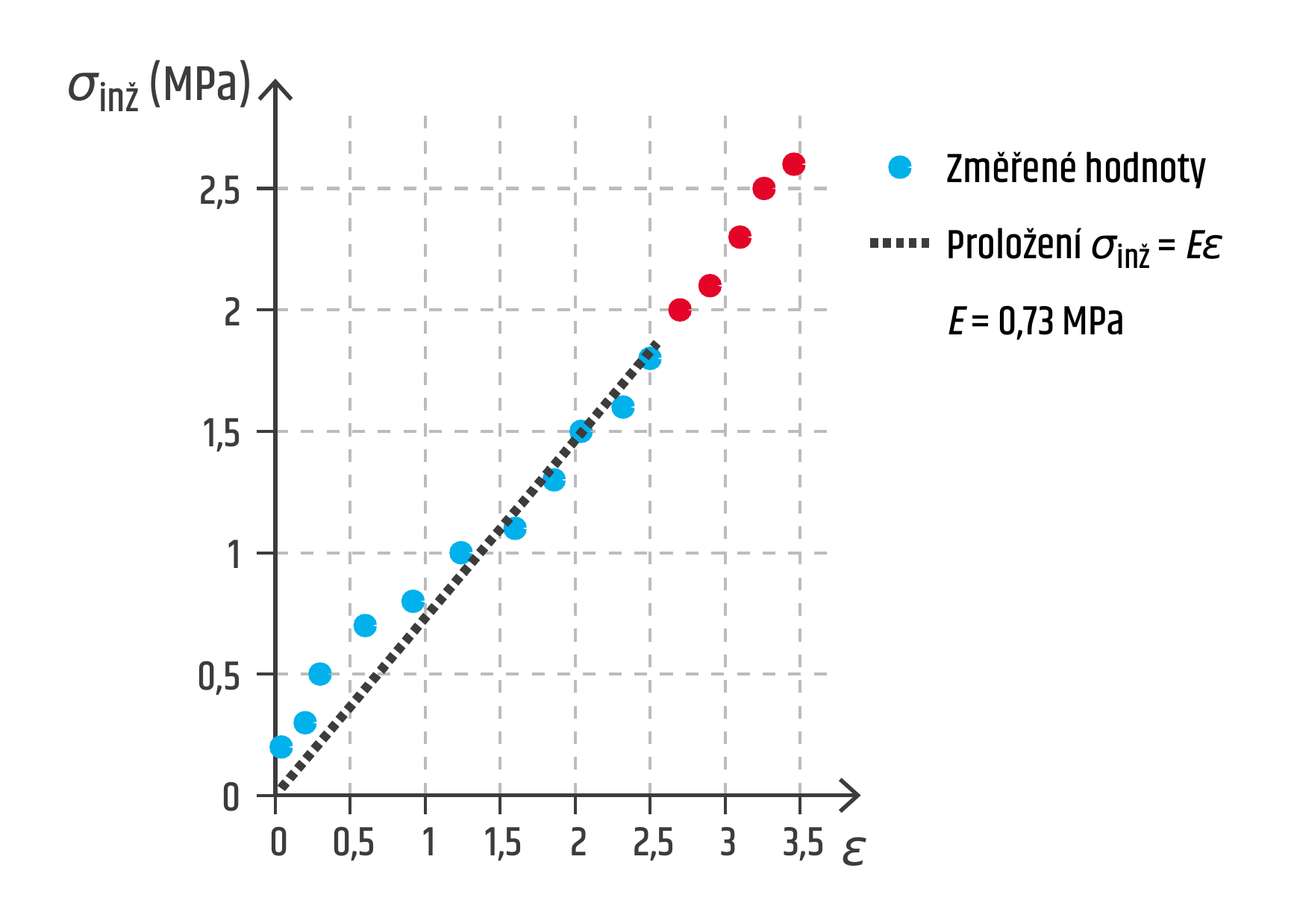
Zdroj
Odečtené hodnoty: \(E=0{,}73\ \mathrm{MPa}\), \(\sigma_B=1{,}8\ \mathrm{MPa}\).

