Kinetická energie a její souvislost s prací

Cvičení 1

Nadhazovač v baseballu hodí míček rychlostí 120 km/h směrem k odpališti. Chytač míček zastaví ve své rukavici.

6.42 - Baseball
Zdroj
  1. Je práce vykonaná nadhazovačem kladná, záporná nebo nulová? Vysvětlete.
  2. Je práce vykonaná chytačem kladná, záporná nebo nulová? Vysvětlete.
  1. Práce vykonaná nadhazovačem je kladná, protože díky ní míček zrychluje a změna jeho pohybové energie je kladná.
  2. Práce vykonaná chytačem je záporná, protože se míček zastaví a změna jeho pohybové energie je záporná.

Cvičení 2

Jakou práci musí vykonat běžec, když zrychlí z klidu na 7,7 m/s? Uvažujte, že jeho hmotnost je 73 kg.

2,2 kJ

Cvičení 3

Kulka o hmotnosti 9,5 g letí rychlostí 1,3 km/s.

  1. Vypočítejte její kinetickou energii.
  2. Jaká by byla kinetická energie kulky, kdyby její rychlost byla pouze poloviční?
  3. Jaká by byla kinetická energie kulky, kdybychom ji dokázali vystřelit dvojnásobnou rychlostí?
  1. 8,0 kJ
  2. energie je čtvrtinová oproti předchozí situaci, tedy 2,0 kJ
  3. energie je čtyřikrát větší než v první části příkladu, protože energie závisí na druhé mocnině rychlosti, tedy 32 kJ

Cvičení 4

Práce W0 je práce potřebná k urychlení automobilu z klidu na 50 km/h.

  1. Je práce potřebná k urychlení tohoto automobilu ze 50 km/h na 150 km/h rovna \(2W_0\), \(3W_0\), \(8W_0\), nebo \(9W_0\)?
  2. Vyberte nejlepší z následujících zdůvodnění:
    1. Práce potřebná k urychlení automobilu závisí na druhé mocnině rychlosti.
    2. Konečná rychlost je třikrát větší než rychlost po vykonání práce W0.
    3. Změna rychlosti z 50 na 150 km/h je dvojnásobek změny rychlosti z 0 na 50 km/h.

a) \(8W_0\) – výpočet:

\[ \begin{aligned} W_0 &= E_{\mathrm{k}1} - E_{\mathrm{k}0} = \frac{1}{2}mv_1^2 - 0 = \frac{1}{2}mv_1^2\\ W_1 &= E_{\mathrm{k}2} - E_{\mathrm{k}1} = \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2 = \frac{1}{2}m(v_2^2 - v_1^2)\\ & = \frac{1}{2}m(9v_1^2 - v_1^2) = \frac{1}{2}m\cdot8v_1^2 = 8\cdot\frac{1}{2}mv_1^2 = 8W_0 \end{aligned}\]

b) nejlepší zdůvodnění je 2); musíme uvažovat změnu \(E_\mathrm{k}\)

Cvičení 5

Borová šiška o hmotnosti 140 g spadne z výšky 16 m na zem. Při dopadu má rychlost 13 m/s.

  1. S jakou rychlostí by dopadla na zem, kdyby nepůsobil odpor vzduchu?
  2. Vykonal odpor vzduchu na šišce kladnou, zápornou nebo nulovou práci? Vysvětlete.
  3. Jak velkou práci vykonaly odporové síly vzduchu?
  4. Určete průměrnou odporovou sílu, kterou vzduch působí na padající borovou šišku.
  1. 17,7 m/s
  2. zápornou (odpor působí proti pohybu tělesa)
  3. −10 J
  4. 0,63 N

Cvičení 6

Curling je olympijský sport. Hraje se s kameny o hmotnosti 18,5 kg na vodorovné ledové ploše. V ideálním případě hráč pustí kámen tak, že na odhodové čáře „hog line“ má rychlost \(v_1=2{,}52\ \mathrm{m/s}\) a zastaví se přesně ve středu kruhů ve vzdálenosti \(d_1=28{,}35\ \mathrm{m}\).

6.43 – Curling (Olympijská kvalifikace, Plzeň 2018)
Zdroj
  1. Proč nelze tření u curlingu zanedbat?
  2. Vyjádřete obecně práci všech sil působících na kámen.
  3. Pomocí prací a kinetické energie určete velikost třecí síly \(F_\mathrm{t}\).
  1. protože by se kámen nikdy nezastavil a hra by nebyla možná
  2. \(W_\mathrm{t}=-F_\mathrm{t}s\)
  3. 2,1 N

Cvičení 7

Automobil o hmotnosti 1100 kg jede po vodorovné cestě rychlostí 19 m/s. Po projetí 32 m dlouhého úseku nezpevněné písčité cesty se jeho rychlost snížila na 12 m/s.

  1. Jaká je celková práce sil působících na automobil? Kladná? Záporná? Nulová? Vysvětlete.
  2. Nalezněte průměrnou velikost výsledné síly působící na automobil v tomto úseku.
  1. záporná, protože se snížila rychlost automobilu a změna jeho kinetické energie je také záporná
  2. 3,7 kN

Cvičení 8

Cyklista o hmotnosti 65 kg jede na kole vážícím 8,8 kg rychlostí 14 m/s.

  1. Jak velkou práci musí vykonat brzdy, aby cyklista zastavil?
  2. Jaká je brzdná vzdálenost, jestliže cyklista zastaví za 4 s?
  3. Jaká je průměrná velikost brzdné síly?

Předpokládáme rovnoměrně zpomalený pohyb, což nemusí odpovídat realitě.

  1. -7,2 kJ
  2. 28 m
  3. 260 N

Cvičení 9

Síla působící na předmět ho posunuje z polohy x = 0 do polohy x = 0,75 m. Její velikost se mění podle následujícího obrázku.

6.44 – Práce proměnné síly
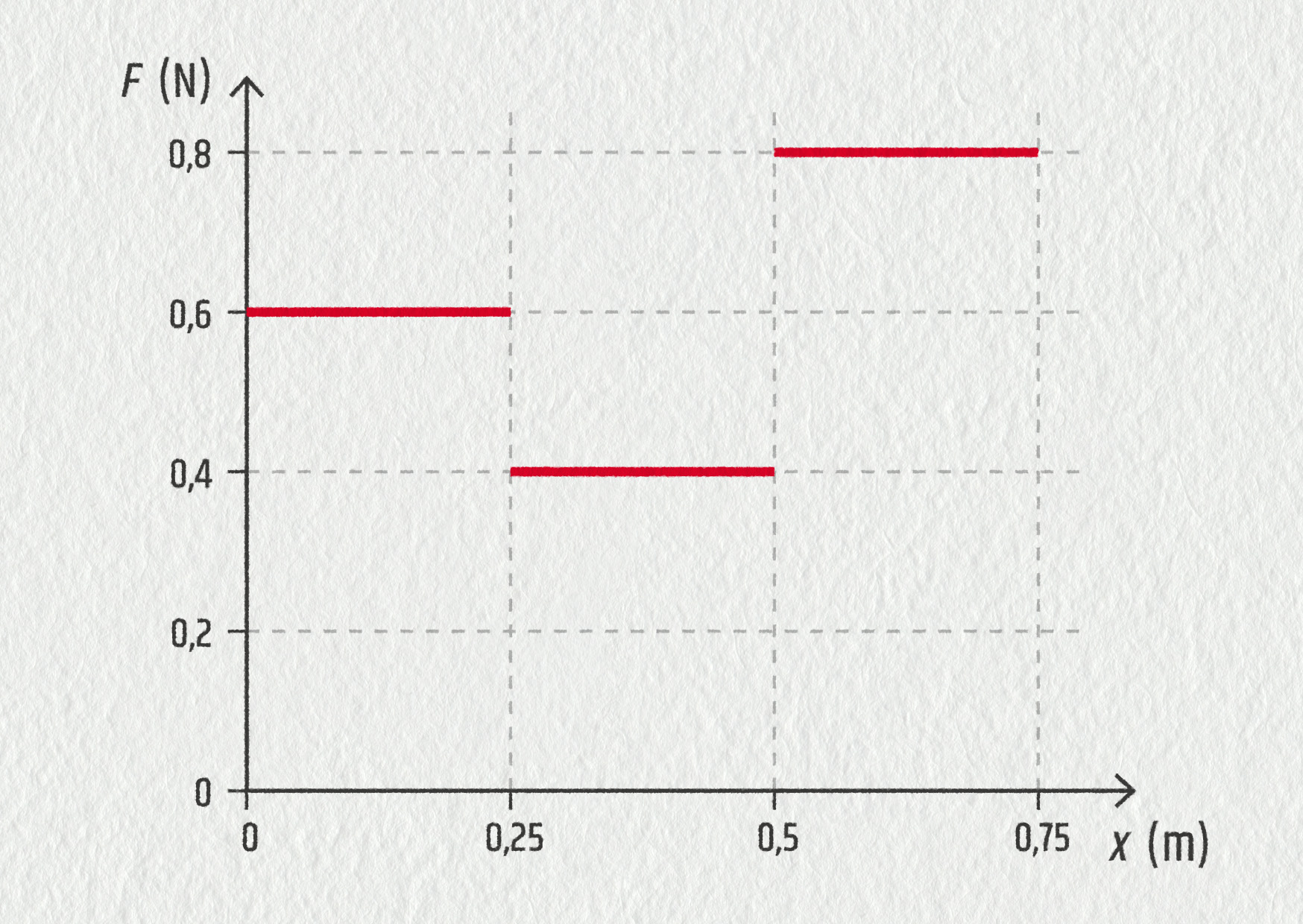
Zdroj
  1. Jak velkou celkovou práci síla vykonala?
  2. Jak velká práce byla silou vykonána, když se předmět pohyboval pouze mezi x = 0,15 m a x = 0,60 m?
  1. 0,45 J
  2. 0,24 J

Cvičení 10

Na předmět působí síla, jejíž velikost se mění podle následujícího obrázku.

Určete celkovou práci vykonanou silou, jejíž velikost se mění podle obrázku. Za předpokladu, že tato síla urychlila kuličku o hmotnosti 60 g, která byla původně v klidu, vypočítejte její výslednou rychlost.

6.45 – Práce proměnné síly
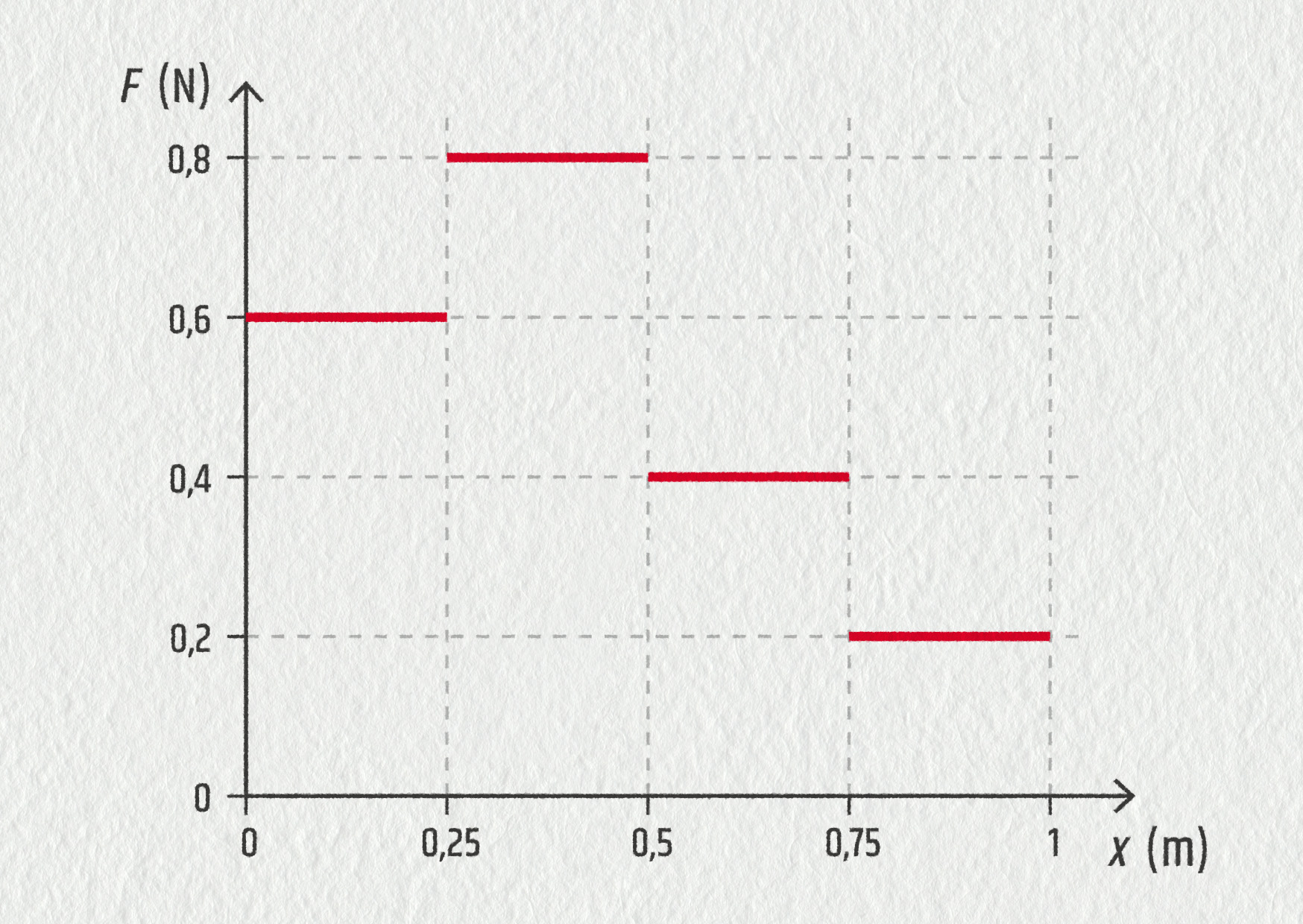
Zdroj

Určete konečnou polohu předmětu, jestliže jeho počáteční poloha je 0,40 m a celková práce vykonaná silou má velikost 0,21 J.

  1. 0,5 J
  2. 4,1 m/s
  3. 0,9 m

Cvičení 11

Určete celkovou práci vykonanou silou, jejíž velikost se mění podle obrázku. Za předpokladu, že tato síla urychlila kuličku o hmotnosti 60 g, která byla původně v klidu, vypočítejte její výslednou rychlost.

6.46 – Práce proměnné síly
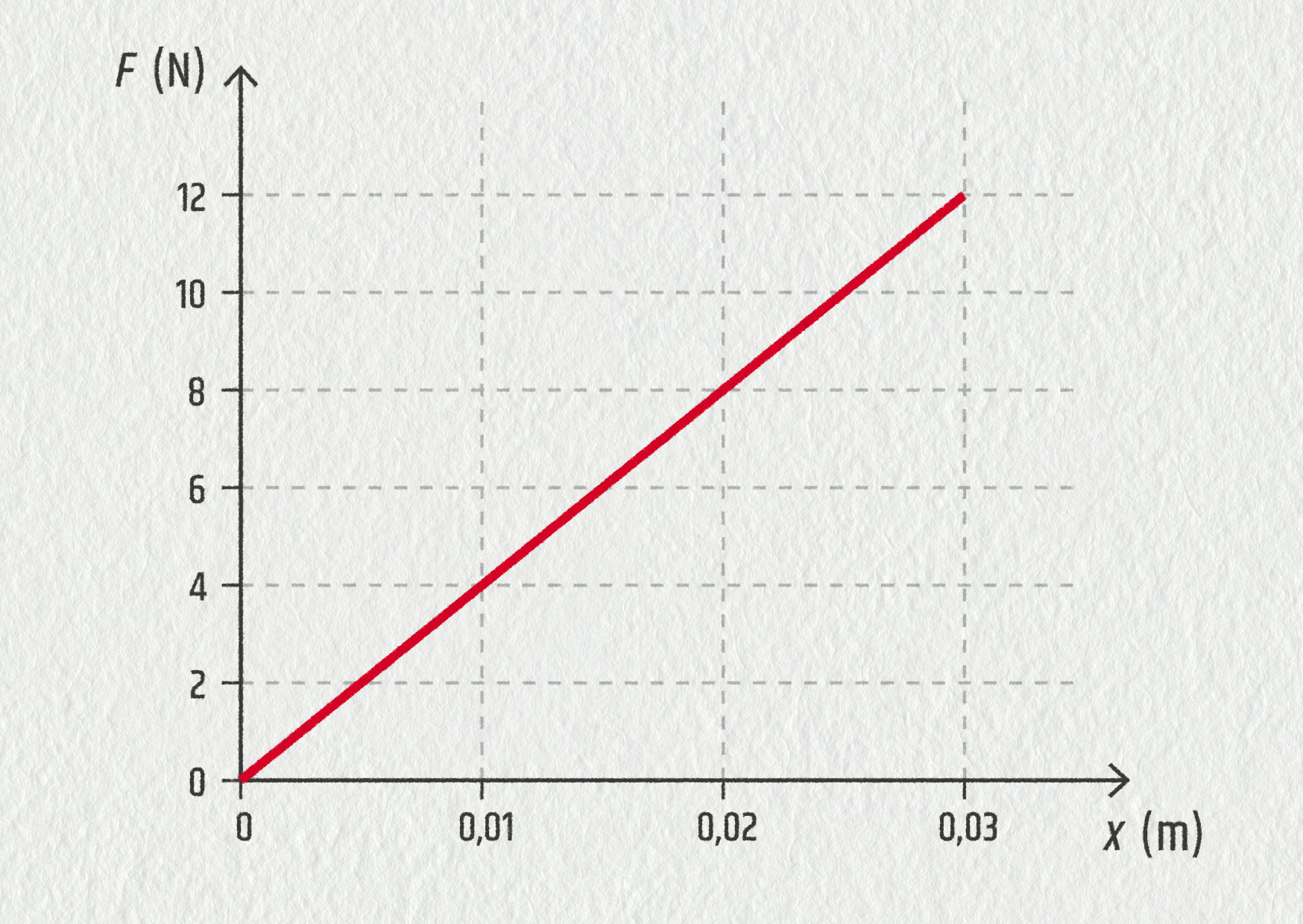
Zdroj
  1. Celková práce: 0,18 J
  2. Výsledná rychlost: 2,4 m/s
Tlačítko pro návrat zpět nahoru na stránce (back to top)