„Horská dráha“ s Hot Wheels
Úkol:
- Prozkoumejte pomocí autíček Hot Wheels zákon zachování mechanické energie.
- Určete práci vykonanou třecími silami v jednotlivých fázích experimentu.
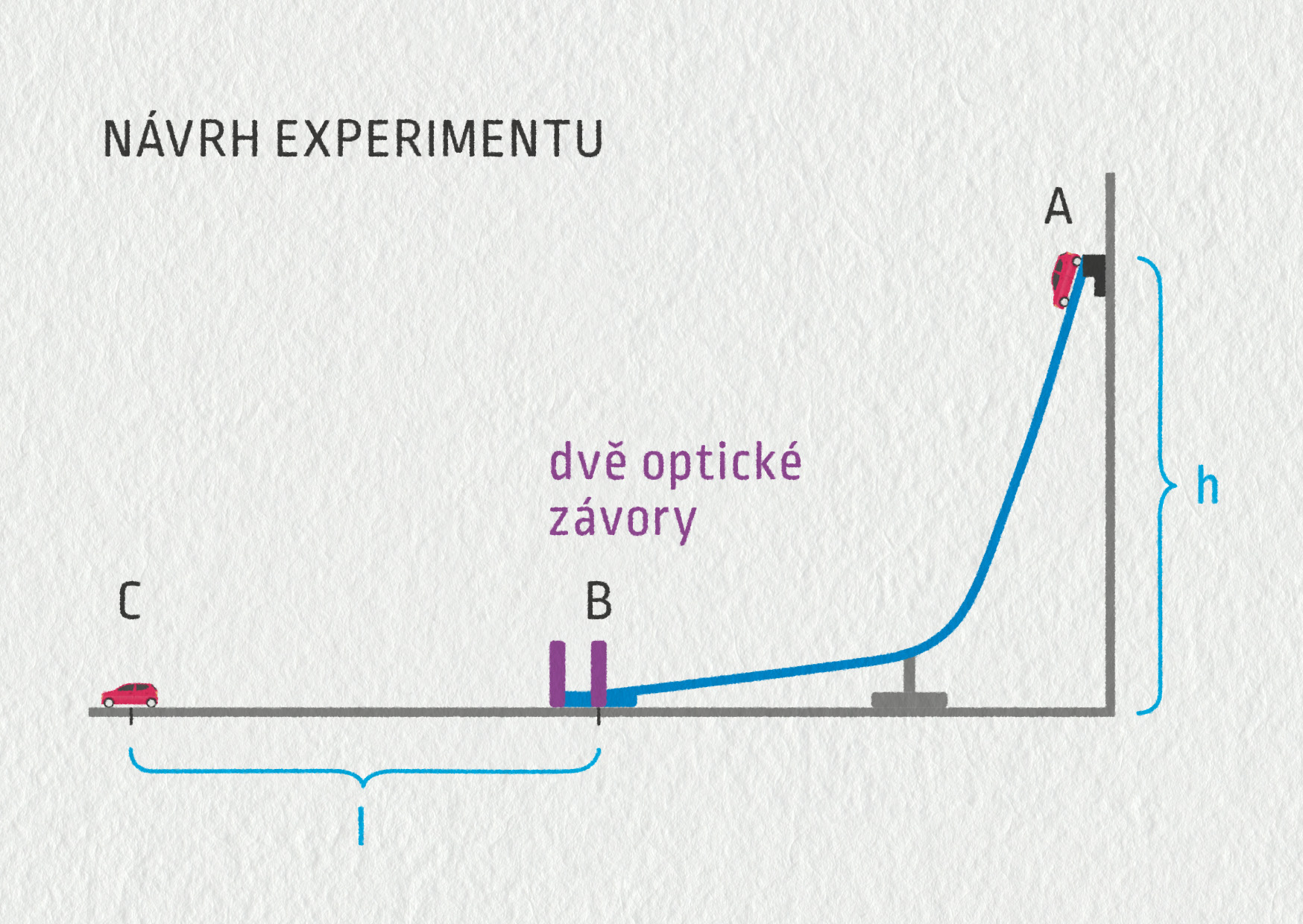
Zdroj
Postup:
- Autíčko pouštíme z nejvyššího bodu dráhy (bod A). Výšku zapíšeme do tabulky a vypočítáme polohovou energii autíčka v počátečním bodě. Kinetická energie je nulová, neboť pouštíme autíčko bez počáteční rychlosti.
- V nejnižším bodě dráhy (bod B) změříme pomocí optické závory (dvou optických závor) rychlost autíčka. Vypočítáme kinetickou energii autíčka.
- Autíčko pokračuje ve svém pohybu po podlaze, ujede vzdálenost l a v bodě C se zastaví. Jeho polohová i kinetická energie jsou nulové. Změříme vzdálenost l.
- Postup několikrát opakujeme a výsledky zapisujeme do tabulky. Můžeme použít různá autíčka, anebo jedno autíčko, které pouštíme z různých výšek.
| bod A | bod B | bod C | úsek AB | úsek BC | ||||
|---|---|---|---|---|---|---|---|---|
| m (g) | h (cm) | EpA (J) | v (m/s) | EkB (J) | l (cm) | změna Em (J) | změna Ek (J) | |
| Auto 1 | ||||||||
| Auto 2 | ||||||||
| Auto 3 | ||||||||
| Auto 4 | ||||||||
| Auto 5 | ||||||||
Otázky:
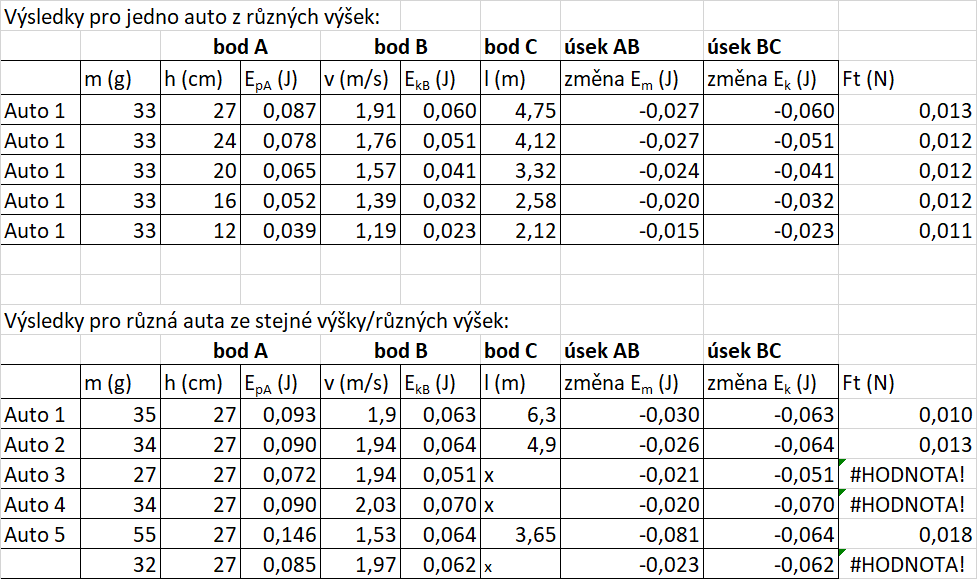
- V prvním úseku dráhy (AB) bychom mohli očekávat, že mechanická energie autíčka \((E_\mathrm{m}=E_\mathrm{p}+E_\mathrm{k})\) zůstane zachována. Jaké jsou vaše výsledky? Odpovídají této teorii? Pokuste se o vysvětlení.
- Ve druhém úseku dráhy (BC) se autíčko pohybuje po vodorovné rovině tak dlouho, až zastaví (nebo do něčeho dříve narazí). Čím je to způsobeno?
- Podívejte se na následující nákres nové dráhy. Může autíčko projet loopingem, když neuvažujeme tření? Stejná otázka s ohledem na naměřené výsledky (uvažujte vliv tření). Co navrhujete, aby byl průjezd auta loopingem bezpečný?

Zdroj
Inspirace: https://science.howstuffworks.com/engineering/structural/roller-coaster.htm
Zdroj

