Cvičení 1
Určete počet dimenzí (1D, 2D, 3D) nutných k popisu těchto pohybů:
- Let letadla
- Vrh koulí
- Pád kamene
Cvičení 2
Uveďte několik příkladů pohybů, kdy můžete, respektive nemůžete nahradit sami sebe hmotným bodem.
Cvičení 3
Jak můžeme měřit okamžitou rychlost pomocí sonaru/radaru?
Cvičení 4
Popište, jak by mohl fungovat tachometr na kole. Zaměřte se na to, jaké veličiny se budou přímo měřit a jak z nich získat hodnotu okamžité a průměrné rychlosti.
Cvičení 5
Akcelerometr v klidu na povrchu Země ukazuje hodnotu 1 g.
- Jakou hodnotu ukáže akcelerometr, který se pohybuje se zrychlením 3 g směrem nahoru?
- Jakou hodnotu ukáže akcelerometr, který padá volným pádem?
- 4 g
- 0 g
Cvičení 6
- Hlemýžď leze rychlostí 5 m za hodinu. Kolik urazí za 1 s?
- Člověk jde rychlostí 5 km/h. Kolik ujde za 1 s?
- Běžný trajekt pluje rychlostí 20 uzlů. Kolik urazí za 1 s?
- Auto jede po dálnici v Kalifornii maximální povolenou rychlostí 65 mph. Kolik ujede za 1 s?
- 1,4 mm
- 1,4 m
- 0,51 m
- 29 m
Cvičení 7
- Vlak TGV jede rychlostí 420 km/h. Za jak dlouho urazí vzdálenost 862 km Marseille–Paříž, pokud nikde nezastavuje?
- Trasu mezi New Yorkem a Londýnem o délce 5600 km zvládají dopravní letadla obvykle zhruba za 6 hodin. V únoru roku 2020 urazil tuto trasu Boeing 747 v rekordním čase 4 hodiny 56 minut. Bylo to díky extrémně silnému proudění vzduchu nad Atlantikem. Vypočítejte (a) obvyklou průměrnou, (b) rekordní průměrnou rychlost letadla.
- 2 h 3 min
- 930 km/h, 1 140 km/h
Cvičení 8
Vlak zrychluje z klidu se stálým zrychlením 2 m/s2.
- Jaká bude jeho rychlost po uplynutí 15 s?
- Za jak dlouho dosáhne rychlosti 40 m/s?
- 30 m/s
- 20 s
Cvičení 9
Míč byl vržen svisle dolů rychlostí 5 m/s. Jeho zrychlení je g = 10 m/s2 směrem dolů.
- Jaká bude jeho rychlost za 1 s?
- Jaká bude jeho rychlost za 2 s?
- Jaká bude jeho rychlost za 3 s?
- 15 m/s
- 25 m/s
- 35 m/s
Cvičení 10
Míč byl vržen svisle vzhůru rychlostí 15 m/s. Jeho zrychlení je g = 10 m/s2 směrem dolů.
- Jaká bude jeho rychlost za 1 s?
- Jaká bude jeho rychlost za 2 s?
- Jaká bude jeho rychlost za 3 s?
- 5 m/s (pohyb směrem nahoru)
- –5 m/s (pohyb směrem dolů)
- –15 m/s (pohyb směrem dolů)
Cvičení 11
John Paul Stapp byl vojenský pilot USA, který v padesátých letech na vlastním těle testoval, jaké přetížení člověk zvládne. Postavil raketové sáně, ve kterých během 5 s od startu dosahoval rychlosti 630 mil za hodinu. Při brždění přežil i rekordní přetížení 46 g. Prudké zastavení mu sice tehdy zlomilo zápěstí a způsobilo dočasnou slepotu, ale jeho výzkum vedl ke zlepšení katapultovacích zařízení v letadlech. Později se přesunul od stíhaček do automobilového průmyslu, kde pomáhal s vývojem bezpečnostních pásů a airbagů.
Jaké bylo průměrné zrychlení raketových sání J. P. Stappa při startu?
Cvičení 12
Graf znázorňuje závislost polohy tří těles na čase. Vyberte všechna správná tvrzení:
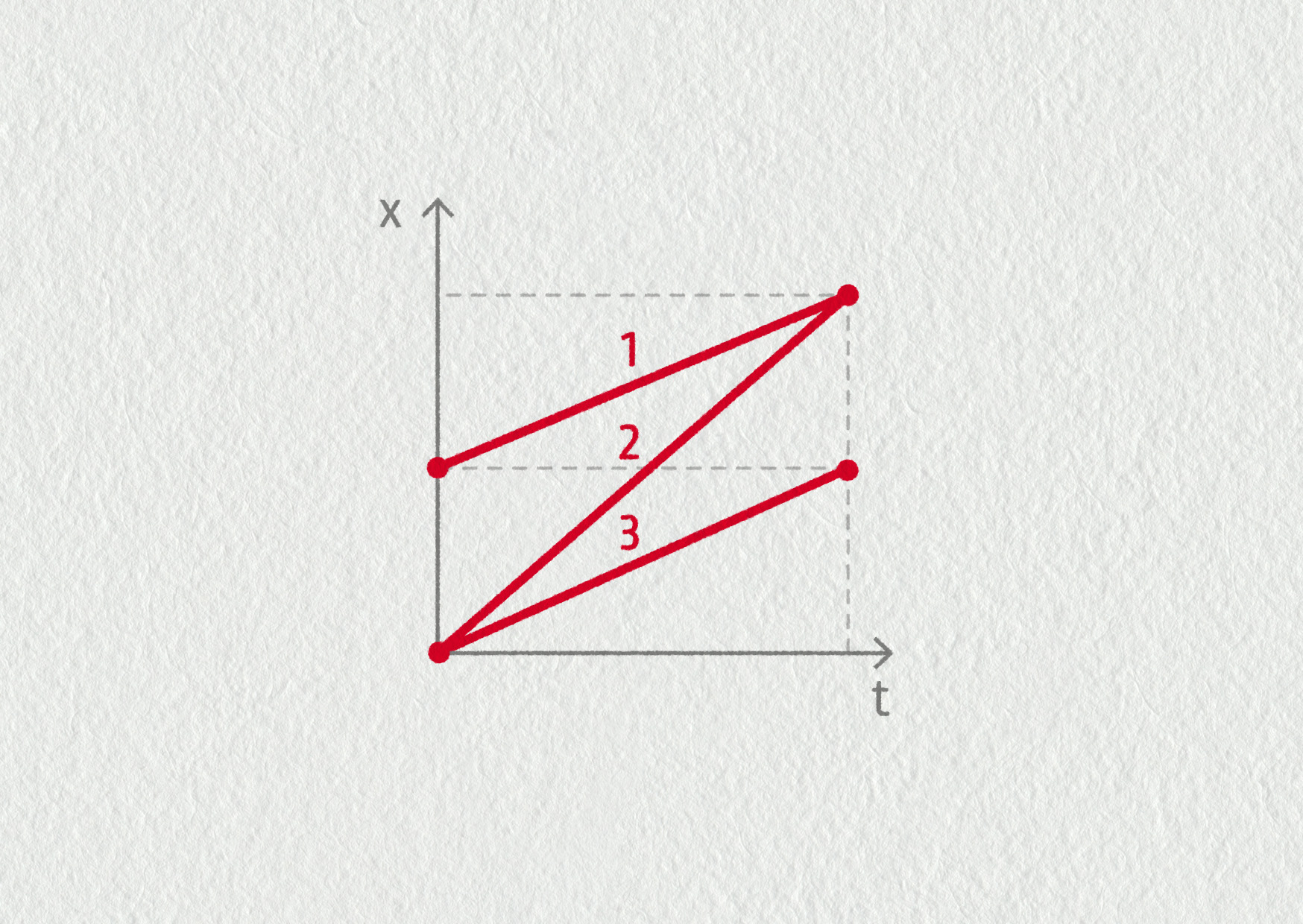
Zdroj
- Těleso 1 urazilo největší dráhu.
- Těleso 2 urazilo největší dráhu.
- Těleso 2 mělo největší rychlost.
- Těleso 3 bylo pomalejší než ostatní.
- Všechna tělesa se pohybovala stejným směrem.
Cvičení 13
Graf znázorňuje závislost rychlosti tří těles na čase. Vyberte všechna správná tvrzení:
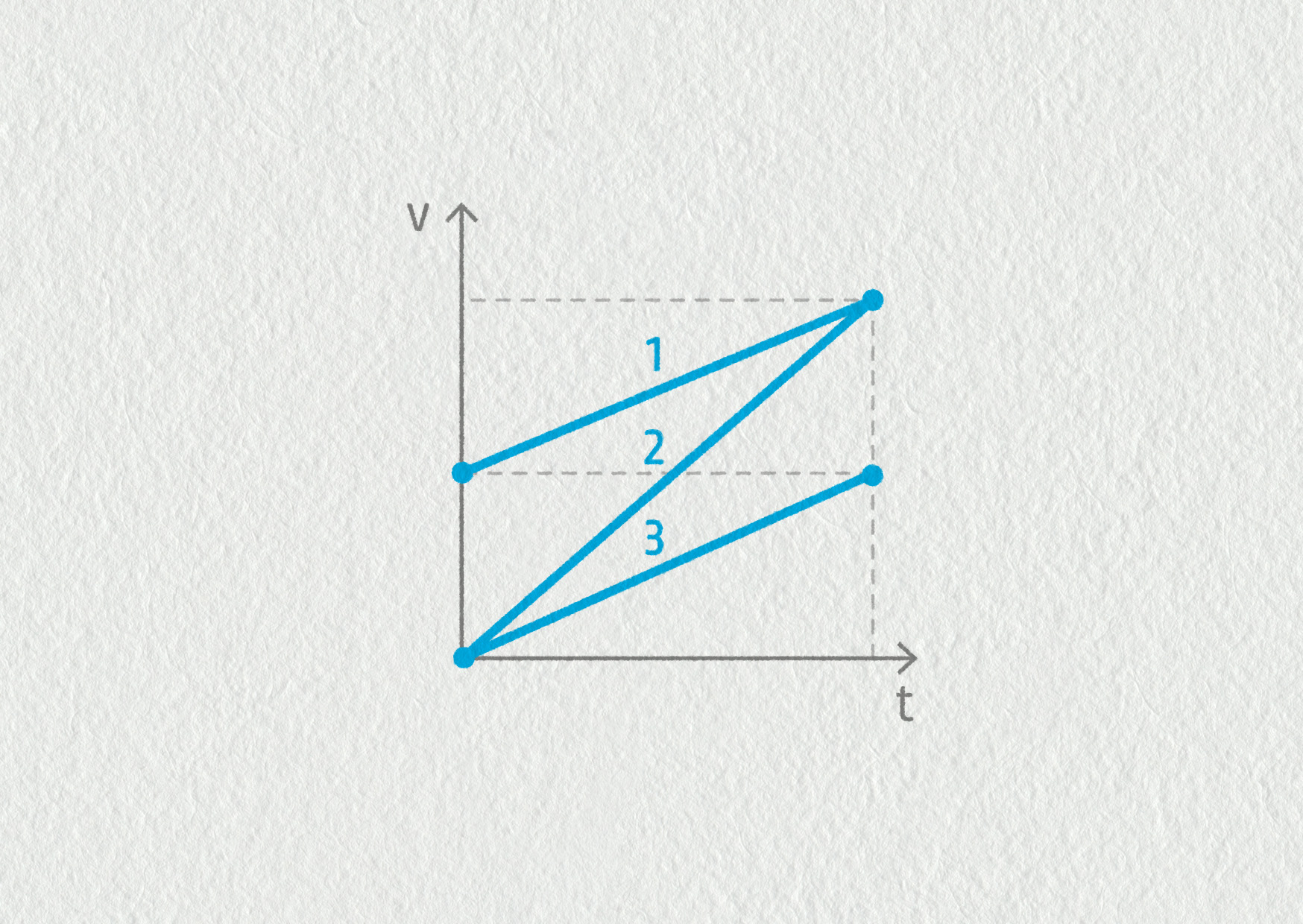
Zdroj
- Těleso 1 urazilo stejnou dráhu jako těleso 3.
- Těleso 2 se pohybovalo nejdéle.
- Těleso 2 mělo největší zrychlení.
- Těleso 3 bylo na začátku v klidu.
- Těleso 1 urazilo největší dráhu.
Cvičení 14
V tabulce vidíte záznam měření polohy sprintera při rozběhu. Z tabulky určete
- průměrnou rychlost v m/s,
- počáteční a koncovou rychlost v m/s a
- průměrné zrychlení v m/s2.
| t (s) | x (cm) |
|---|---|
| 0,00 | 6 |
| 0,07 | 10 |
| 0,14 | 15 |
| 0,21 | 23 |
| 0,28 | 34 |
| 0,35 | 43 |
| 0,42 | 58 |
| 0,49 | 72 |
| 0,56 | 87 |
| 0,63 | 101 |
| 0,70 | 114 |
| 0,85 | 130 |
- vP = 1,46 m/s;
- počáteční v1 = 0,57 m/s, koncová v2 = 1,10 m/s;
- zrychlení a = 0,62 m/s2.
Cvičení 15
Graf ukazuje záznam měření polohy automobilu při brždění. Z grafu určete (a) průměrnou rychlost auta, (b) počáteční rychlost auta.
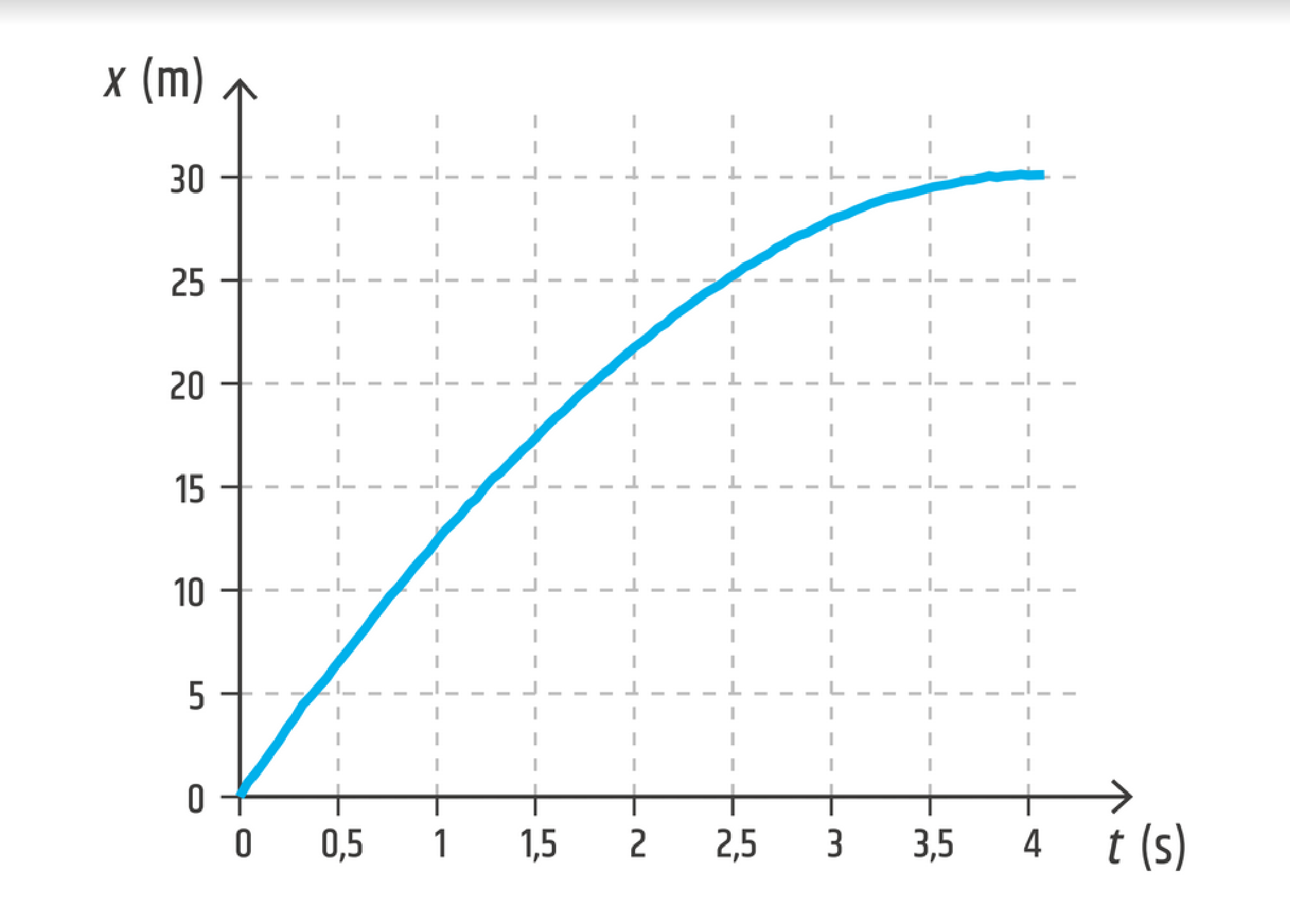
Zdroj
Cvičení 16
Cvičení 17
- Jak dlouho bude trvat celá její plavba o délce 60 km?
- Jaká bude průměrná rychlost lodi?
- 4,5 h
- vP = 13 km/h
Cvičení 18
Na obrázku vidíte graf pro polohu tří vlaků mezi stanicemi Horní, Střední a Dolní. Takovému typu grafu se v dopravě říká grafikon. Z grafu určete:
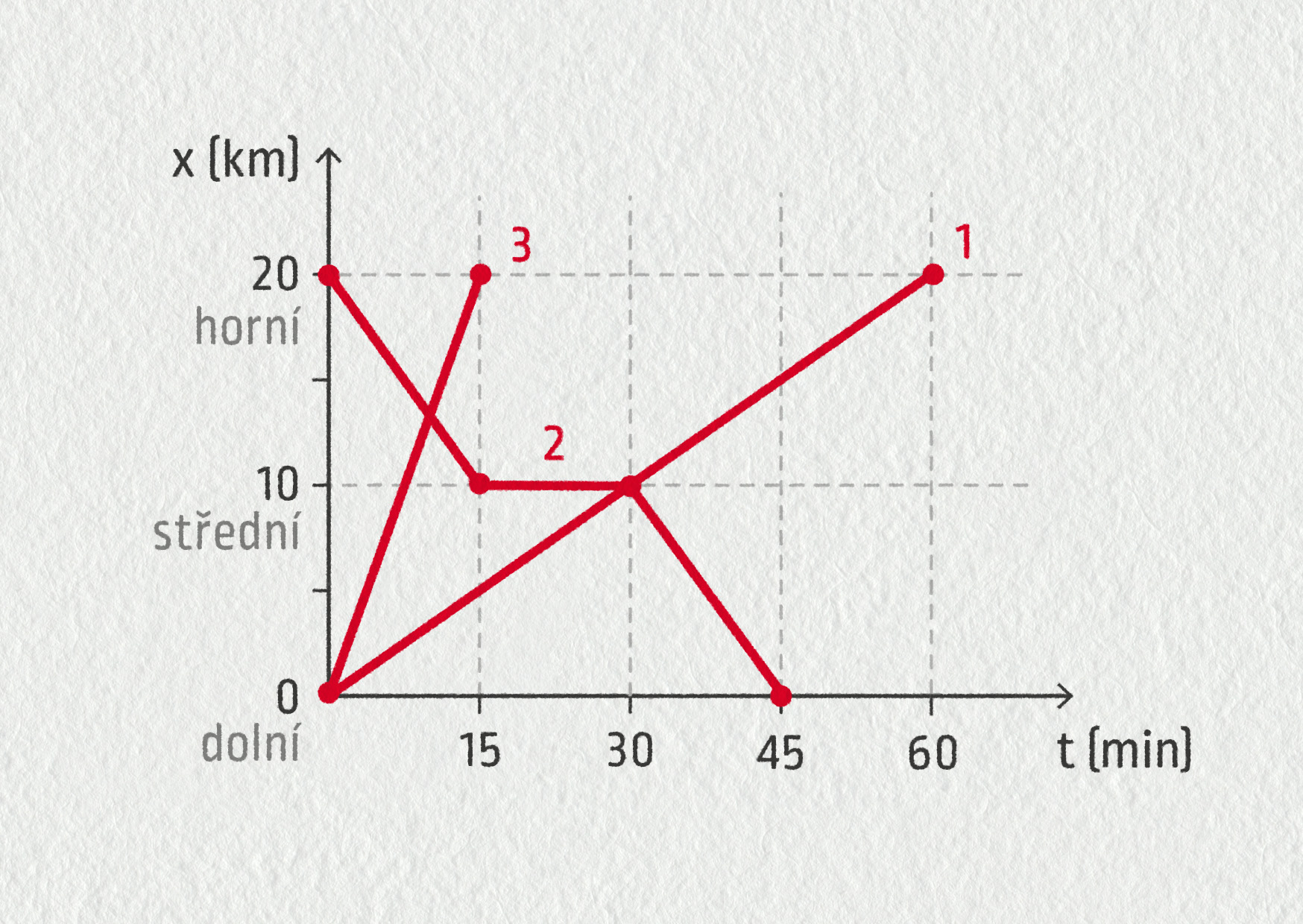
Zdroj
- Průměrnou rychlost jízdy všech tří vlaků.
- Průměrnou rychlost vlaku 2 na celé jeho trase.
- Místo a čas setkání 1 a 2.
- Místo a čas setkání 2 a 3.
- v1 = 20 km/h, v2 = 40 km/h, v3 = 80 km/h
- vP = 27 km/h
- x = 10 km, t = 30 min
- x = 13 km, t = 10 min
Cvičení 19
Následující úlohu prý museli vyřešit uchazeči o úřednické pozice ve staré Číně. Dokážete to i vy?
Host ujde za den 300 li. Host vyšel od hostitele, ale zapomněl si oděv. Když po 1/3 dne hostitel objevil zapomenutý oděv, vydal se na cestu, aby hosta dohonil. Když předal oděv hostovi, ihned obrátil koně na zpáteční cestu. Za 3/4 dne (od odjezdu hosta) byl opět doma. Kolik li by hostitel ujel na koni za jeden den? Pro větší přehlednost doplňte řešení grafem.
Cvičení 20
Cvičení 21
Cvičení 22
Cvičení 23
Podle slavného spisovatele Julese Vernea se měli lidé na Měsíc dostat pomocí obřího děla s hlavní dlouhou 220 m. Přestože Verne ve svých knihách často předpověděl vývoj techniky na léta dopředu, tentokrát se dopustil fatální chyby. Projektil s cestovateli musí dosáhnout druhé kosmické rychlosti 11 200 m/s, aby opustil zemské gravitační pole.
- Jaké by muselo být zrychlení projektilu v dělové hlavni podle Julese Verna?
- Jaká by musela být délka hlavně, aby bylo možné přežít start projektilu? Zrychlení by v tomto případě nemělo přesáhnout 5 g.
- 290 000 m/s2
- 1300 km
Cvičení 24
Kosmická loď se pohybuje se stálým zrychlením 9,8 m/s2. Za jak dlouho by dosáhla loď jedné desetiny rychlosti světla, startuje-li z klidu? Jakou dráhu by přitom urazila?
Cvičení 25
Souprava metra se smí pohybovat podle těchto pravidel: maximální rychlost 60 km/h, maximální zrychlení ±2 m/s2. Jaká je nejkratší možná doba potřebná k jízdě mezi dvěma stanicemi vzdálenými 2000 m? Pro větší přehlednost doplňte řešení grafy x(t) a v(t).

