Triangulace

Úkol: Změřte vzdálenost pomocí triangulace.

Vybavení: malý stolek, svinovací metr, deska s úhloměrem, několik špendlíků, izolepa a nůžky

Triangulace je metoda umožňující měření vzdálenosti pomocí měření úhlů. Vychází z toho, že pokud u trojúhelníku známe délku jedné strany a vnitřní úhly, dokážeme určit jeho zbývající strany. Využijeme k tomu goniometrické funkce.

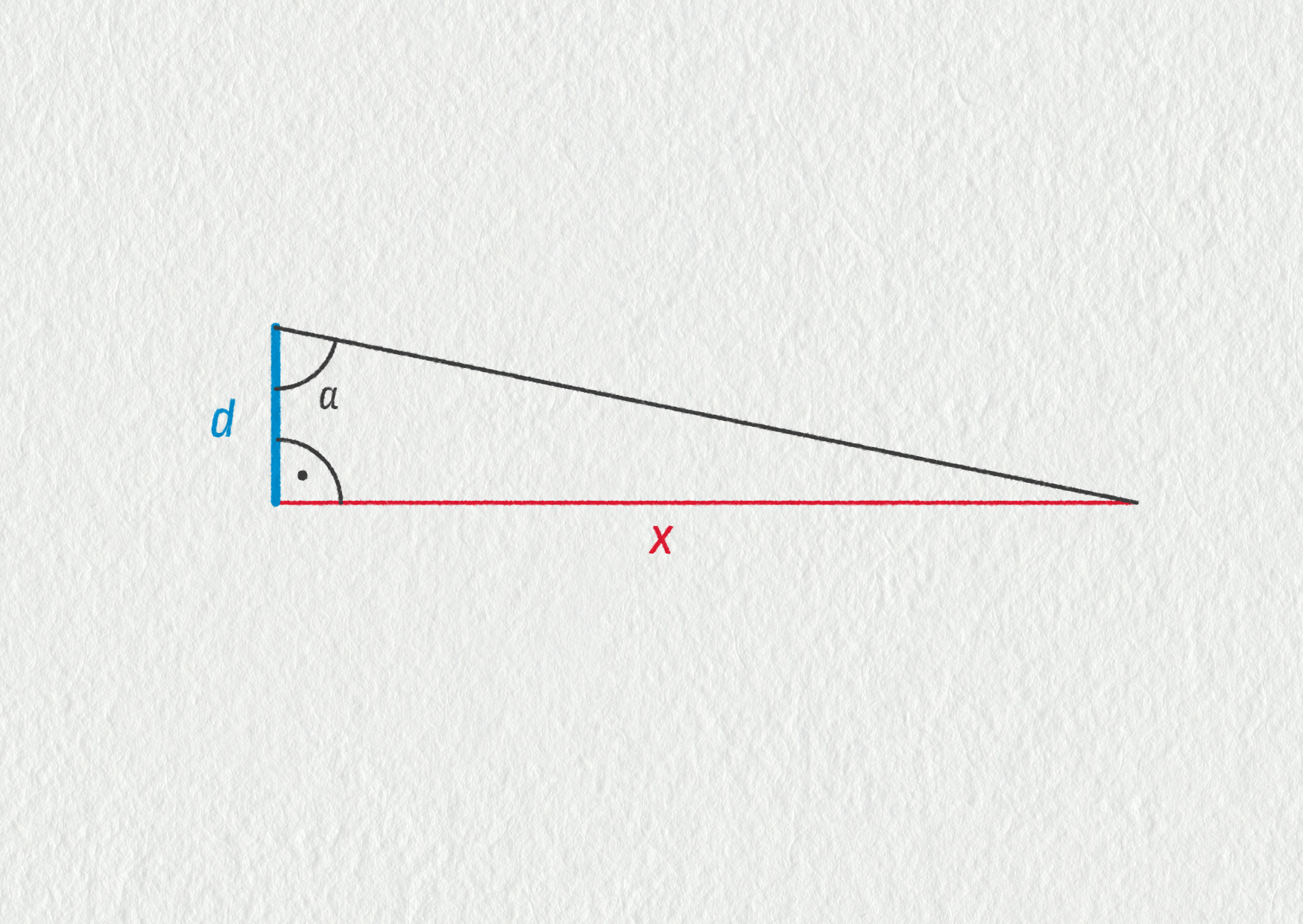
Vcelku jednoduché je to u pravoúhlého trojúhelníku, u kterého známe jednu odvěsnu (v obrázku modrá – označená d) a úhly u ní. Vzdálenost třetího vrcholu od odvěsny je pak:

\(x = d\mathop{\mathrm{tg}}(\alpha)\)

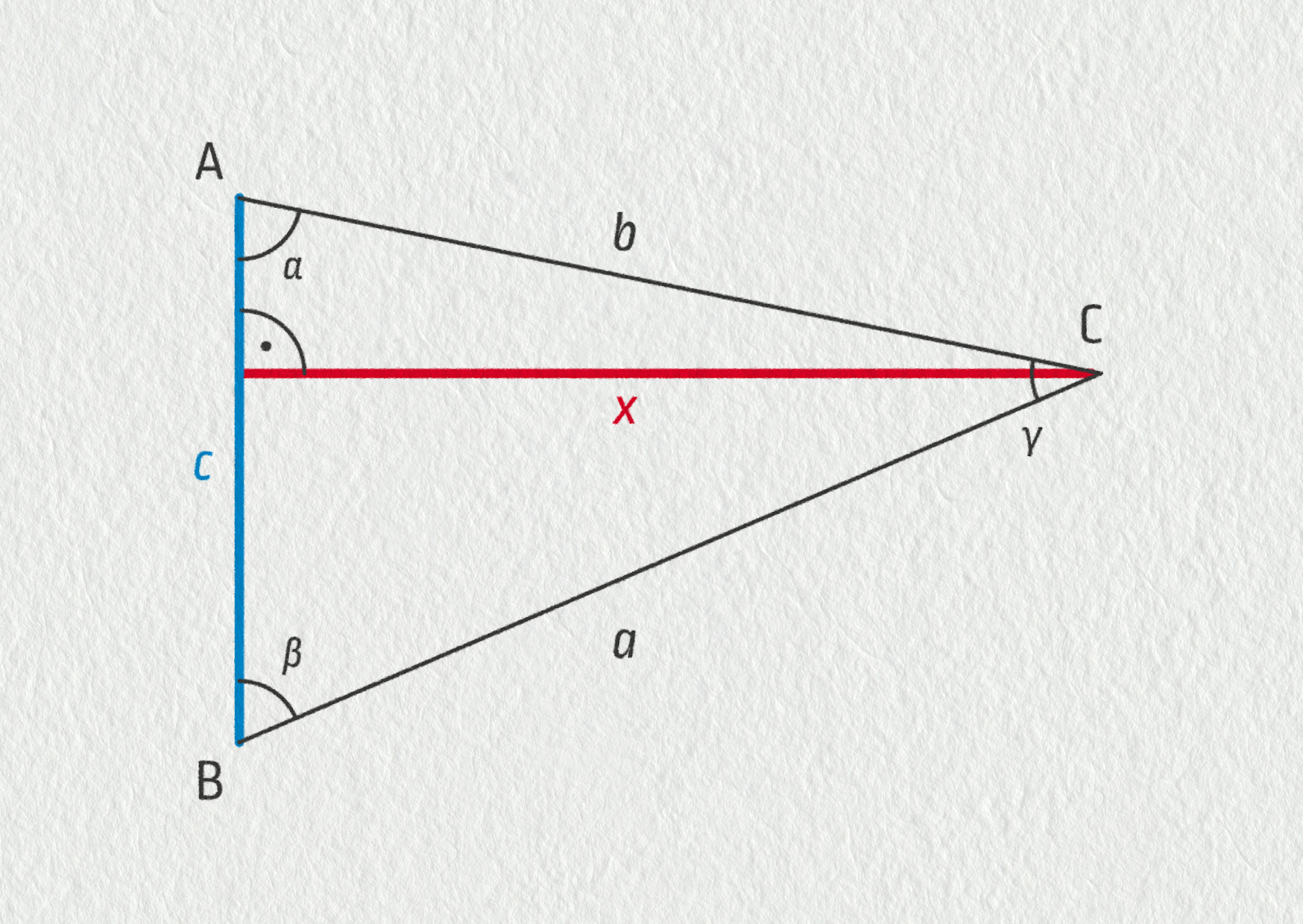
U obecného trojúhelníku musíme znát oba úhly u základní strany (věta usu). Výšku trojúhelníku (tj. vzdálenost třetího vrcholu od základní strany) určíme buď rýsováním, nebo pomocí vzorce:

\(\displaystyle x=\frac{c\sin(\alpha)\sin(\beta)}{\sin(180^\circ-\alpha-\beta)}\)

Poznámka na okraj: Odvození pro zájemce

Tento vztah lze odvodit ze základních vlastností trojúhelníka. Vrcholy trojúhelníku si označíme A, B a C, patu výšky P. Úhel γ si spočítáme ze známých úhlů α a β. V trojúhelníku ACP platí, že \(x/b = \sin(\alpha)\), z toho \(x = b\sin(\alpha)\). Stranu b vyjádříme pomocí sinové věty v trojúhelníku ABC: \(\sin(\beta)/b = \sin(\gamma)/c\) , z toho \(b = c \sin(\beta)/\sin(\gamma)\). Po dosazení dostáváme \(x = c \sin(\alpha) \sin(\beta)/\sin(\gamma)\).

Postup měření v pravoúhlém trojúhelníku

K tomuto měření nutně potřebujete dvě kolmé čáry – ideální jsou linie na školním hřišti. Cílem měření je určení vzdálenosti brankových čar.

1. Jedním z vrcholů měřeného trojúhelníku je roh hřiště. Vyberte si na brankové čáře své stanoviště. Změřte vzdálenost svého stanoviště od rohu hřiště.
2. Postavte stolek na svém stanovišti a na něj položte desku s úhloměrem tak, aby základna úhloměru ležela na brankové čáře. To ověříte tím, že si na konce základny úhloměru zapíchnete dva špendlíky a podíváte se podél nich – měli byste vidět roh hřiště (nebo pomocníka, který na něm stojí).
3. Zapíchněte špendlík do středu úhloměru, dívejte se přes něj a druhý špendlík zapíchněte tak, abyste přes něj viděli protější roh hřiště. Na úhloměru změřte zaznamenaný úhel.
4. Z naměřených hodnot spočítejte vzdálenost protějšího rohu.

Postup měření v obecném trojúhelníku

Na přípravu a provedení je toto měření snazší než předchozí postup. Potřebujete dva stolky a dva úhloměry.

1. Vyberte si v terénu libovolnou úsečku, jejíž délku změříte (třeba šířku ulice před školou). Třetím vrcholem trojúhelníku je libovolná dominanta ležící přibližně kolmo na zvolenou úsečku (věž kostela, komín, roh domu).
2. Umístěte úhloměry na oba konce zvolené úsečky tak, aby jejich základna ležela na úsečce (stejně jako v předchozím postupu zkontrolujte pohledem přes špendlíky).
3. Změřte úhel mezi úsečkou a zvolenou dominantou. Totéž zopakujete na druhém konci základní úsečky.
4. Z naměřené délky základní úsečky a obou úhlů spočítejte vzdálenost dominanty.

Otázky:

1. Zkuste porovnat vypočítané hodnoty se skutečnými vzdálenostmi. Jaká je odchylka?
2. Jaký vliv má nejistota měření úhlu na vypočítaný výsledek?
3. Jaké možnosti zpřesnění měření vás napadají?

Poznámky pro učitele

1. Místo stolku můžete použít židli s vodorovným sedákem. V extrémním provedení se deska s úhloměrem pokládá na zem, ale pak si žáci musejí při měření lehat.

2. Deska pro měření je z pěnového polystyrenu nebo silnější vlnité lepenky (tak, aby do ní šlo zapichovat špendlíky).

3. Úhloměr vytiskněte z tohoto souboru.

4. Měření na školním hřišti: pokud na hřišti měří několik skupin současně, odměřují si základnu svého trojúhelníku od stejného rohu, liší se tedy její délkou. Po výpočtech srovnají zjištěné délky hřiště. Měla by následovat diskuze o tom, jaký vliv má přesnost měření na spolehlivost výsledku.

Reálně 191 metrů

d [m]	9,9	9,9	9,9
α [stupně]	89	89	89
β [stupně]	86	87	88
x [m]	113,3	141,7	189

Nejprve je nutné zjistit délku hřiště přímým měřením (pásmem nebo z letecké mapy). Výsledky triangulace se většinou liší v jednotkách metrů. Je vhodné zpracovat naměřené hodnoty v tabulkovém kalkulátoru. Kalkulátor umožňuje měnit vstupní hodnoty a sledovat, jak se mění hodnoty spočítané. V případě školního hřiště jsou délky základny a hřiště řádově srovnatelné. Proto vycházejí vcelku rozumné výsledky.

Reálně 40 metrů

d [m]	5	9	12	15
α [stupně]	82	78	73	69
tg(α)	7,11	4,7	3,27	2,6
x [m]	35,6	42,3	39,2	39,1

Závislost na délce základy

d [m]	14,9	15	15,1
α [stupně]	69	69	69
tg(α)	2,6	2,6	2,6
x [m]	38,8	39,1	39,3

Závislost na velikosti úhlu

d [m]	15	15	15
α [stupně]	68	69	70
tg(α)	2,47	2,6	2,75
x [m]	37,1	39,1	41,2

5. Měření dominanty z obecného trojúhelníku: pokud pracuje více skupin, spojte je po dvou, každá dvojice skupin měří vlastní dominantu.

Při měření vzdálené dominanty (tj. ze základny cca 10 metrů se odměřuje vzdálenost stovek metrů), odchylují se spočítané výsledky od reality o desítky procent. Opět je vhodné vložit naměřené hodnoty do tabulkového kalkulátoru a vyzkoušet vliv nepřesnosti měření.