Matematické kyvadlo
Úkol:
- Z experimentu vyvoďte vztah mezi periodou kmitání a hmotností zavěšeného tělesa.
- Z experimentu vyvoďte vztah mezi periodou kmitání a délkou závěsu.
Vybavení: pevný stojan, tenký provázek nebo režná nit, závaží, stopky
Provedení: Matematické kyvadlo je tvořeno tělesem zavěšeným na tenkém vlákně konstantní délky, jehož hmotnost je zanedbatelná ve srovnání s hmotností tělesa \(m\). Délkou závěsu \(L\) budeme rozumět vzdálenost bodu závěsu od těžiště zavěšeného tělesa.
V tomto praktiku se omezíme na kmity s malou výchylkou, při nichž se neprojeví závislost periody na amplitudě. Požadujeme-li přesnost lepší než 0,2 %, maximální úhel, který svírá provázek se svislým směrem, nesmí překročit 10°. Prakticky to znamená, že při délce závěsu \(L=100\ \mathrm{cm}\) by neměla vodorovná výchylka překročit 17 cm, při délce \(L=20\ \mathrm{cm}\) bude maximální vodorovná výchylka 3,4 cm.
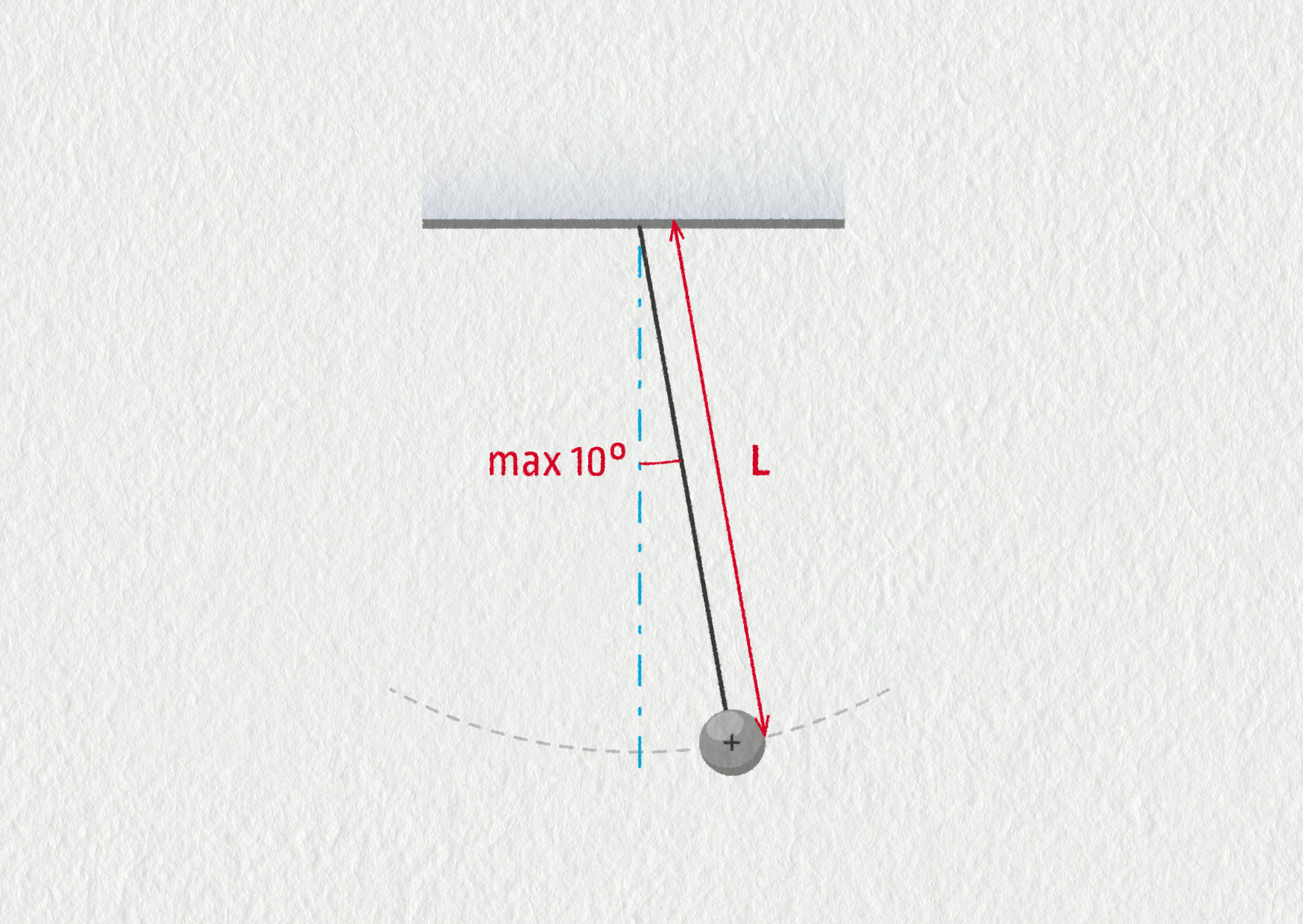
Zdroj
Perioda \(T\) je doba trvání jednoho kmitu (pohyb tam a zpět). Aby bylo určování času stopkami dostatečně přesné, doporučujeme vždy změřit dobu alespoň pěti kmitů. Velmi se osvědčuje, když čas měří současně dva lidé a výslednou hodnotu (průměr) si zapíší jen v případě, že se jejich výsledky liší o méně než 0,2 s.
- Prozkoumejte, jak závisí perioda kmitání \(T\) na hmotnosti závaží \(m\) (při konstantní délce závěsu).
- Prozkoumejte, jak závisí perioda kmitání \(T\) na délce závěsu \(L\).
Otázky:
- Jaká je nejistota \(\Delta T\) měření periody stopkami? Podle velikosti \(\Delta T\) správně zaokrouhlete hodnoty periody \(T\).
- Jaký je vztah mezi \(T\) a \(m\)?
- Sestrojte graf závislosti \(T\) na \(L\) a body proložte vhodnou křivkou. O jakou funkci se jedná?
- Souhlasí typ funkce a číselná hodnota experimentální konstanty se vztahem uvedeným ve výkladu?

