Co je to kmitání?
Houpačka, kterou jste jako děti určitě měli rádi, je typickým příkladem kmitajícího tělesa. Kmity (neboli oscilace) jsou až překvapivě častý druh pohybu, a zaslouží si svou vlastní kapitolu. Pojďme se zamyslet, jak kmitání vzniká a co je pro ně charakteristické.

Zdroj
V klidu visí naše houpačka ve stabilní rovnovážné poloze. Stačí do ní lehce šťouchnout a již bez nutnosti dalšího působení sama pokračuje v periodickém pohybu tam a zpět, dokud se třením nezastaví opět v rovnovážné poloze. To je možné díky tomu, že působící síly (v našem případě gravitační síla spolu s tahovou silou závěsu) vrací houpačku neustále zpět do rovnovážné polohy. Silám, které táhnou těleso do rovnovážné polohy, říkáme vratné síly. Dalo by se říci, že kde je vratná síla, tam může vzniknout kmitání.
Uveďme si další příklady mechanických oscilátorů. Struna kytary může kmitat, protože ji síla pružnosti neustále vrací zpět do přímého tvaru. Podobné je to s napjatou blánou bubnu, membránou mikrofonu nebo ušním bubínkem. Jsou to pružná tělesa, která kmitají, jen to často není vidět, protože jejich pohyb je rychlý a má malou výchylku. Kmitat ale mohou také celé mosty či budovy nebo také lodě na vodní hladině.
Vraťme se ještě jednou k houpačce. Sami jste si možná všimli, že frekvenci pohybu konkrétní houpačky nelze změnit. Je to vlastnost daná fyzickými parametry kmitajícího systému. Fyzikové říkají houpačce kyvadlo a právě kyvadlo se stalo základem prvních přesných hodin, protože frekvence kývání je neměnná, a určuje tak jejich přesný chod.
Kmitající těleso nazýváme odborně mechanický oscilátor a jeho vlastnosti můžeme shrnout takto:
- Oscilátor kmitá tam a zpět kolem rovnovážné polohy.
- Příčinou vzniku kmitů je vratná síla, která neustále vrací těleso zpět do rovnovážné polohy.
- Pro oscilátory je typické, že mají jednu či více vlastních frekvencí kmitání. Vlastní frekvence kmitání je dána fyzickými parametry kmitajícího systému.
Kmitání se neomezuje jen na mechaniku. Oscilace jsou obecně chápány jako periodické změny nějaké veličiny kolem centrální hodnoty. V kapitole 20 jsme zkoumali střídavý proud, který je příkladem elektromagnetického kmitání v obvodech. V živé přírodě můžeme najít velmi zajímavé biochemické oscilátory. Takovým případem je třeba srdce, které samo udržuje svůj pravidelný rytmus, nebo suprachiasmatická jádra v mozku, která řídí náš cirkadiánní rytmus s periodou 24 hodin. Kmity najdeme dokonce i v ekonomii – v případě hospodářského cyklu ekonomika v určité oblasti nesetrvává v rovnovážném stavu, ale kmitá okolo něj. To se projevuje jako pravidelné opakování ekonomického růstu a následného poklesu.
Perioda a frekvence
Kmitání je pravidelně se opakující pohyb kolem rovnovážné polohy. Pojmem kmit rozumíme právě jeden elementární pohyb, který se pořád dokola opakuje. S pravidelností tohoto pohybu jsou spojeny veličiny perioda a frekvence, se kterými jste se již setkali v předchozích kapitolách. Připomeňme si, jak jsou definovány.
Perioda \(T\) je doba trvání jednoho kmitu. Jednotkou periody je sekunda s.
Frekvence \(f\) udává počet kmitů za sekundu. Jednotkou frekvence je hertz Hz.
Platí \(f=1/T\).
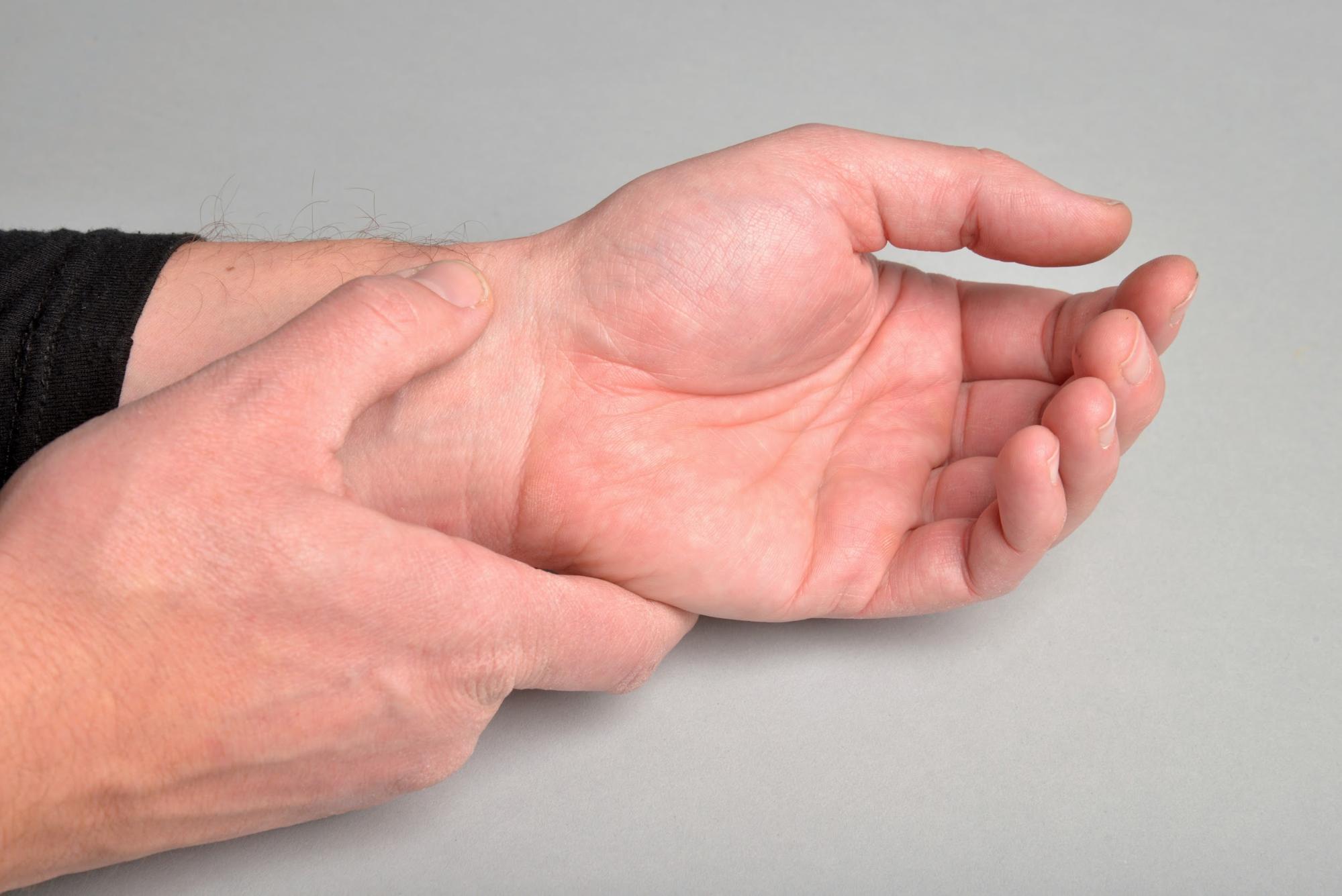
S jakou frekvencí kmitá váš srdeční sval? – Změřte si svoji tepovou frekvenci.
Puls můžete snadno ucítit hmatem v místech, kde tepny procházejí blízko kožního povrchu. Vyzkoušejte například tepnu spánkovou na spáncích nebo tepnu vřetenní v zápěstní jamce. Pro zpřesnění výsledku doporučujeme změřit počet tepů za minutu a frekvenci následně dopočítat. Při 72 tepech za minutu je frekvence
\[ f = \frac{72\ \hbox{tepů}}{60\ \mathrm{s}} = 1{,}2\ \mathrm{Hz} \]a perioda \(T=1/f=0{,}83\ \mathrm{s}\). Klidová tepová frekvence člověka se pohybuje v intervalu mezi 60 a 90 tepy za minutu. Poznamenejme, že když na začátku 17. století Galileo Galilei objevoval základy mechaniky, neměl k dispozici stopky a k měření času využíval právě svůj puls.
Zdroj
Amplituda a výchylka
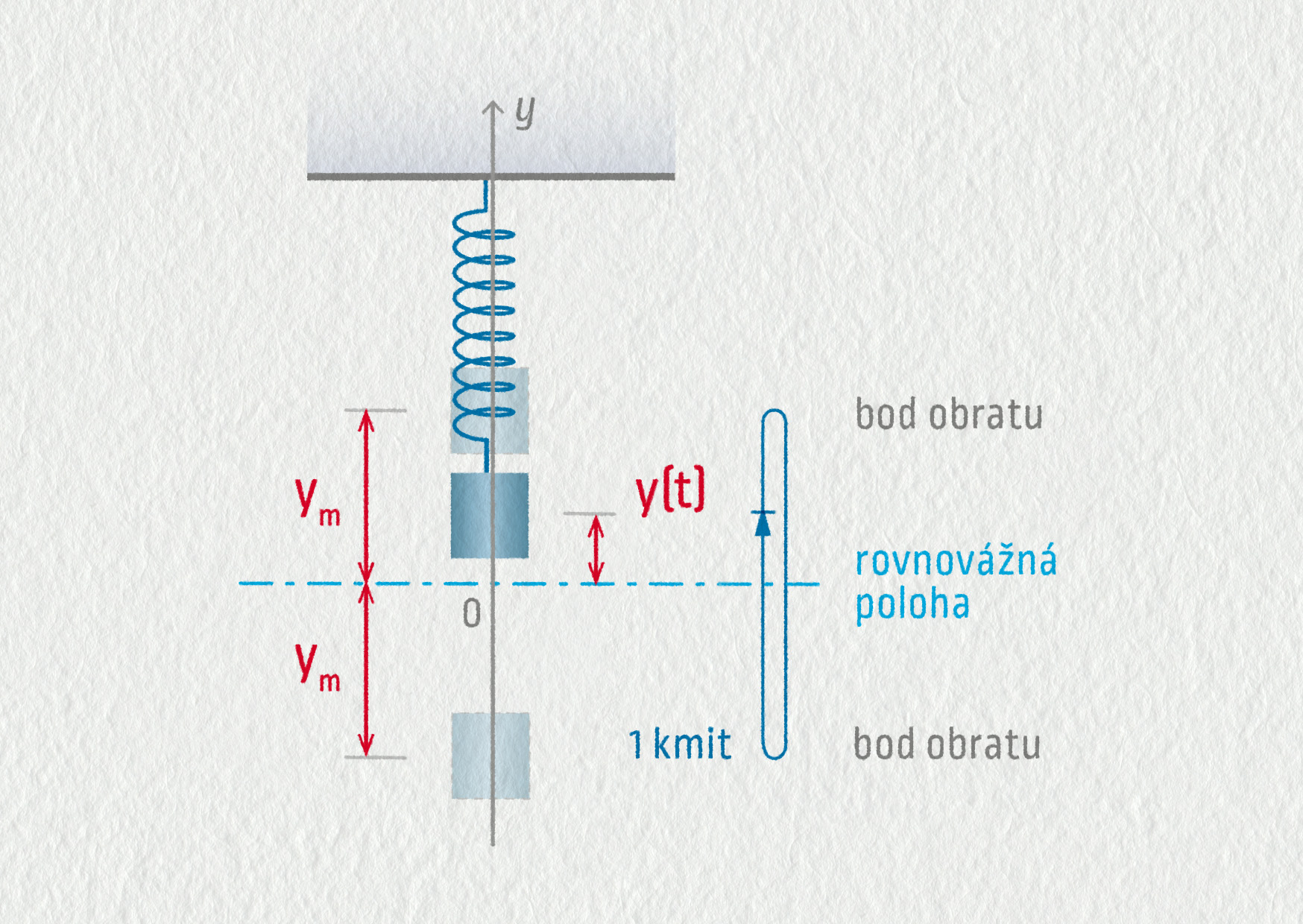
Maximální výchylka oscilátoru z rovnovážné polohy se nazývá amplituda výchylky. Je to tedy vzdálenost bodu obratu od rovnovážné polohy. Kmitá-li těleso vodorovně ve směru osy \(x\), značí se amplituda \(x_\mathrm{m}\), kmitá-li svisle podél osy \(y\), pak se amplituda značí \(y_\mathrm{m}\).
Okamžitá výchylka je výchylka oscilátoru z rovnovážné polohy v určitém čase. Okamžitou výchylku značíme \(x(t)\), pokud těleso kmitá ve vodorovném směru, nebo \(y(t)\) při kmitání ve svislém směru. Jedná se vlastně o x-ovou, resp. y-ovou souřadnici tělesa v čase \(t\), která se neustále mění. Pojmy kmit, amplituda a okamžitá výchylka si ukažme konkrétně na příkladu pružinového oscilátoru a kyvadla.
Zdroj
Svislý pružinový oscilátor vznikne zavěšením tělesa na pružinu v tíhovém poli. Pokud nekmitá, setrvává těleso v rovnovážné poloze. Na obrázku 21.7 je zachycena situace, kdy těleso kmitá: znázorněna je jeho okamžitá výchylka \(y(t)\) v čase \(t\) a body obratu odpovídající amplitudě \(y_\mathrm{m}\). Jak plyne čas, souřadnice \(y(t)\) se mění. Kmitání probíhá ve svislém směru, proto k jeho popisu postačí jen osa \(y\), jejíž počátek O byl umístěn do rovnovážné polohy.
Zdroj
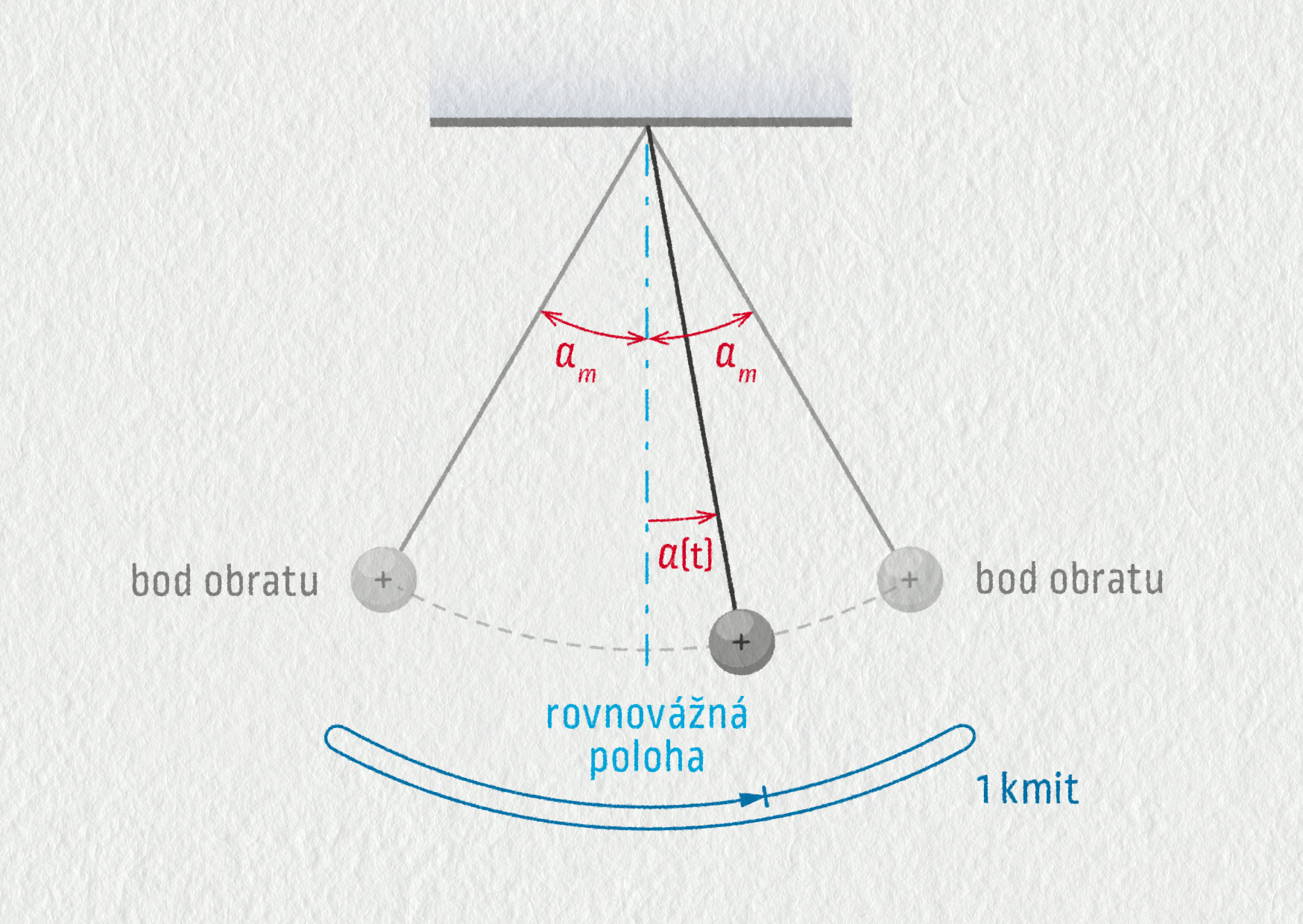
Kyvadlo je těleso zavěšené v pevném bodě pomocí provázku nebo tyče konstantní délky. Po uvolnění bez počáteční rychlosti opisuje ve svislé rovině trajektorii, která je částí kružnice. Rovnovážná poloha je zřejmě nejnižším bodem trajektorie. K popisu polohy bychom mohli používat souřadnice tělesa \(x(t)\) a \(y(t)\), ale u kyvadla je mnohem elegantnější určovat polohu pomocí úhlu \(\alpha\), o který se těleso vychýlilo ze svislého směru. Vidíme zde opět měnící se okamžitou výchylku \(\alpha(t)\), amplitudu výchylky \(\alpha_\mathrm{m}\) a naznačen je i jeden kmit.
Harmonické kmitání
Chceme-li vědět, jak těleso kmitá, musíme zjistit, jak závisí okamžitá výchylka na čase. Experimentálně můžeme tuto závislost zkoumat pomocí sonaru, jak ukazuje obrázek 21.9.

Zdroj
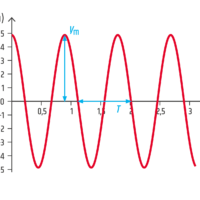
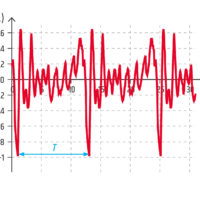
U nejjednodušších oscilátorů má časová závislost výchylky sinusový průběh. Takto kmitající systém nazýváme harmonickým oscilátorem. Harmonicky kmitají tělesa, u nichž je vratná síla přímo úměrná výchylce z rovnovážné polohy (např. pružinový oscilátor, v přiblížení malých výchylek též kyvadlo).
Existují však kmitající systémy, kdy se pohyb sice pravidelně opakuje – je periodický, ale časová závislost výchylky nemá přesně sinusový průběh. Takto neharmonicky kmitá například membrána mikrofonu, který zaznamenává zpívaný tón.
Porovnání harmonického a neharmonického kmitání
Zdroj
Zdroj
Popisovat harmonické kmitání jsme se učili na elektrických veličinách ve 20. kapitole. Graf sinusového průběhu odpovídá obecné matematické funkci \(y=A\sin(Bx+C)+D\), kde \(A\), \(B\), \(C\) a \(D\) jsou konstanty. Vliv těchto konstant na podobu grafu si vyzkoušejte v apletu https://www.geogebra.org/m/zbgnkw4d.
Fyzikálně odpovídá
- konstanta \(A\) amplitudě kmitání \(y_\mathrm{m}\),
- konstanta \(B\) úhlové frekvenci \(\omega=2\pi f\),
- konstanta \(C\) počáteční fázi \(\varphi_0\),
- konstanta \(D\) vzdálenosti rovnovážné polohy od počátku soustavy souřadnic.
Velmi často volíme soustavu souřadnic tak, aby její počátek ležel v rovnovážné poloze, kolem které těleso kmitá. Potom je konstanta \(D\) nulová a pro okamžitou výchylku získáváme následující předpis:
Časová závislost výchylky harmonického oscilátoru
\[ y = y_\mathrm{m}\sin(\omega t+\varphi_0) \]\(y_\mathrm{m}\) – amplituda,
\(\omega\) – úhlová frekvence,
\(\varphi_0\) – počáteční fáze.
Fyzikální význam parametrů byl vysvětlen ve 20. kapitole, takže pokud chápete, můžete tuto poznámku přeskočit :-).
Úhlová frekvence \(\omega\) (řecké písmeno omega) je definována pomocí frekvence, respektive periody kmitání vztahem
\[ \omega = 2\pi f = \frac{2\pi}T \]Její jednotkou je radián za sekundu (rad ⋅ s−1).
Úhlová frekvence je pojítkem mezi počtem opakování děje za časovou jednotku a odpovídající změnou argumentu funkce sinus za časovou jednotku.
Jak známo, funkce \(y=\sin(x)\) je periodická s periodou \(2\pi\), neboť platí \(y=\sin(x)=\sin(2\pi+x)\) pro libovolné \(x\). Průběh fyzikálního pohybu (okamžitá výchylka oscilátoru) se začne opakovat po uplynutí časové periody \(T\), takže výchylka oscilátoru v čase \(t=0\) a \(t=T\) musí být stejná pro libovolné \(y_\mathrm{m}\) a \(\varphi_0\):
\[ y = y_\mathrm{m}\sin(\varphi_0) = y_\mathrm{m}\sin(\omega T+\varphi_0) \]Porovnáním s předchozím vztahem zjišťujeme, že \(\omega T\) musí být rovno \(2\pi\).
Počáteční fáze \(\varphi_0\) (řecké písmeno fí, index nula) se vyjadřuje v radiánech. V grafu určuje, kde sinusoida protíná svislou osu. Číselně stanovuje, v jaké fázi kmitání se právě soustava nachází, když ji v okamžiku \(t=0\ \mathrm{s}\) začínáme pozorovat. To znamená, jestli měření spouštíme, když se oscilátor nachází v horním bodu obratu (\(\varphi_0=\pi/2\ \mathrm{rad}\) – čtvrtina periody), v rovnovážné poloze (\(\varphi_0=0\ \mathrm{rad}\) nebo \(\varphi_0=\pi\ \mathrm{rad}\)), v dolním bodu obratu (\(\varphi_0=3\pi/2\ \mathrm{rad}\) – tři čtvrtiny periody) nebo ještě v jiném bodě svojí trajektorie. Vyzkoušejte si to v animaci https://www.geogebra.org/m/zbgnkw4d.
Poznamenejme, že ve výrazu \(y_\mathrm{m}\sin(\omega t+\varphi_0)\) se argument funkce sinus nazývá okamžitá fáze kmitání, značí se písmenem \(\varphi=\varphi_0+\omega t\) a vyjadřuje se v radiánech.
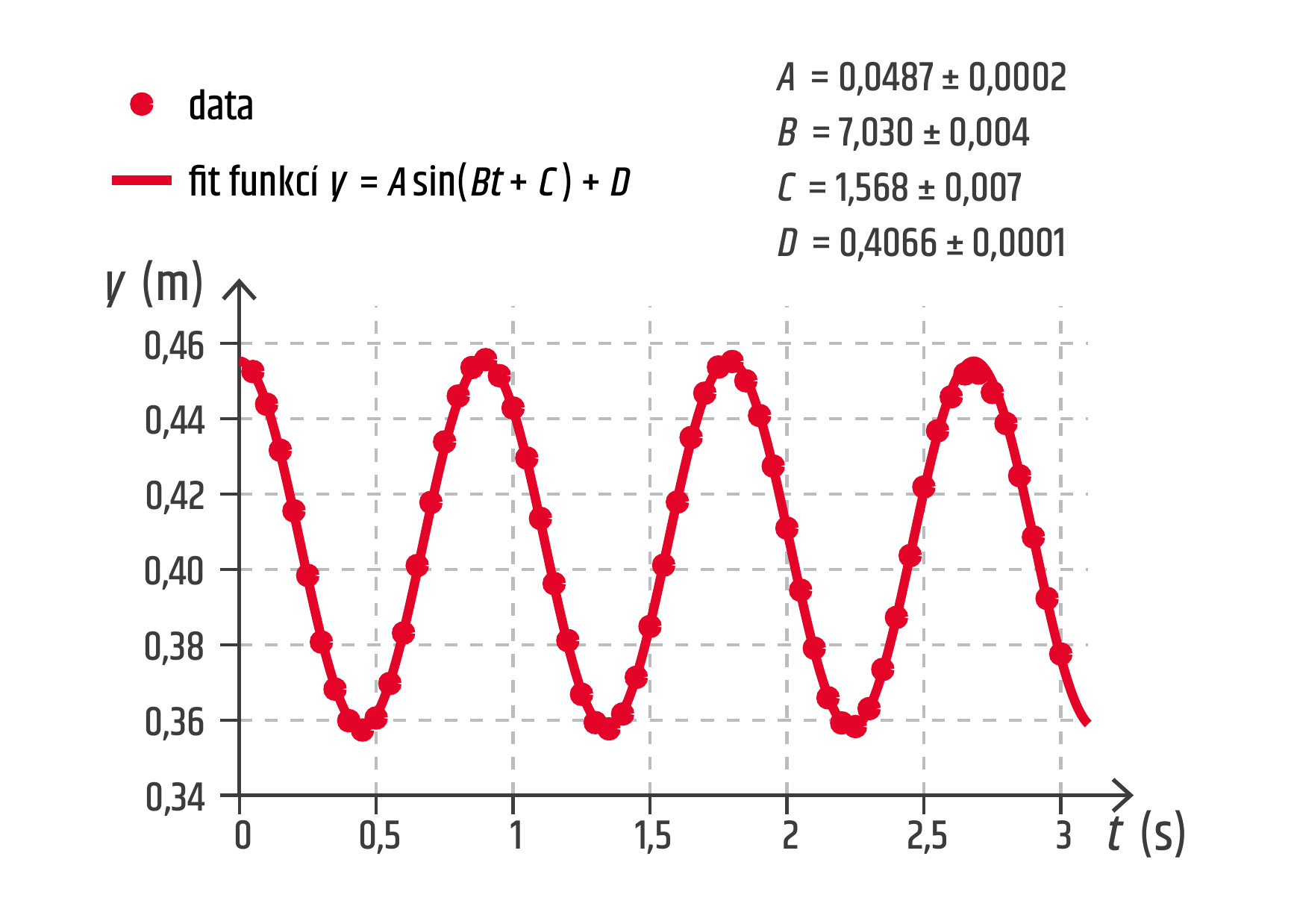
Graf 21.11 zobrazuje výsledek měření sonarem v experimentu vyfoceném na obrázku 21.9. Experimentálními body byla proložena sinusoida \(y=A\sin(Bx+C)+D\) a numericky byly dopočítány hodnoty konstant. Určete fyzikální význam konstant a jejich hodnoty a jednotky. Vypočítejte frekvenci a periodu tohoto pohybu.
Zdroj
Přímým porovnáním s fyzikálním vztahem pro výchylku \(y(t)=y_\mathrm{m}\sin(\omega t+\varphi_0)\) zjišťujeme, že
- konstanta \(A\) představuje amplitudu čili maximální výchylku z rovnovážné polohy, \(y_\mathrm{m}=0{,}0487\ \mathrm{m}=4{,}87\ \mathrm{cm}\),
- konstanta \(B\) má význam úhlové frekvence \(\omega=7{,}030\ \mathrm{rad/s}\),
- konstanta \(C\) je počáteční fáze \(\varphi_0=1{,}568\ \mathrm{rad}\),
- konstanta \(D\) znamená vzdálenost rovnovážné polohy oscilátoru od sonaru, \(D=0{,}4066\ \mathrm{m}=40{,}66\ \mathrm{cm}\).
Odsud můžeme dopočítat frekvenci kmitání \(f=\omega/2\pi=1{,}12\ \mathrm{Hz}\) a periodu \(T=1/f=0{,}894\ \mathrm{s}\).
Poznámka pro šikovné: Program, který naměřenými daty proložil sinusoidu, dopočítal ke každému parametru i jeho nejistotu. Takto systematicky bychom měli vyjadřovat nejistoty u každého výsledku experimentu, takže bychom měli psát např. \(y_\mathrm{m}=(0{,}0487\pm0{,}0002)\ \mathrm{m}= (4{,}87\pm0{,}02)\ \mathrm{cm}\). Jelikož frekvenci i periodu počítáme z úhlové frekvence zatížené nejistotou \(\omega=(7{,}030\pm0{,}004)\ \mathrm{rad/s}\), budou i tyto dvě veličiny zatíženy nejistotou. Podle pravidel pro nejistoty vyložených v kapitole 2 je výsledkem experimentu \(f=(1{,}1188\pm0{,}0006)\ \mathrm{Hz}\) a \(T=(0{,}8938\pm0{,}0005)\ \mathrm{s}\).
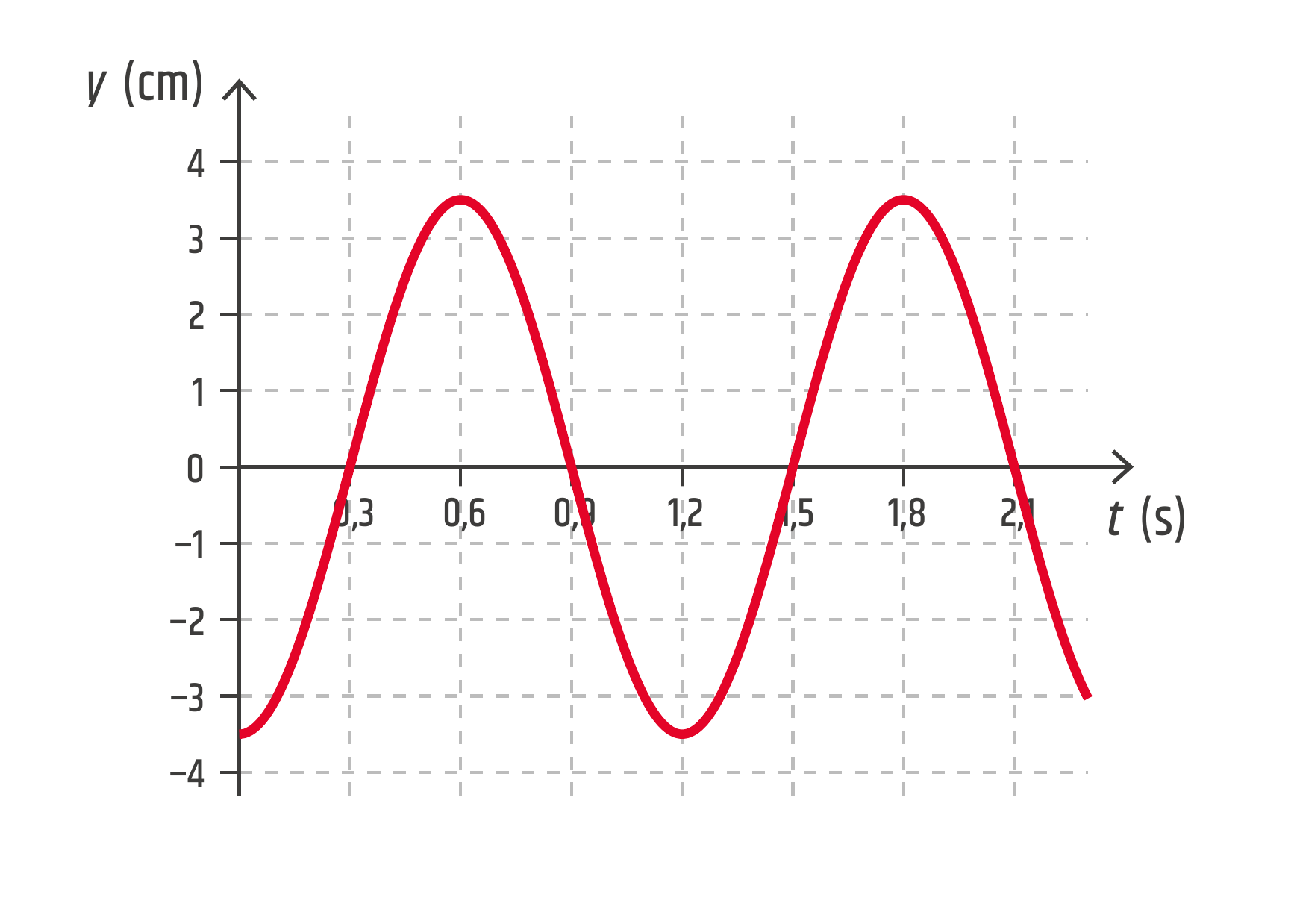
Graf 21.12 znázorňuje závislost výchylky na čase. Určete periodu, frekvenci a amplitudu kmitání.
Zdroj
Rychlost a zrychlení v závislosti na čase
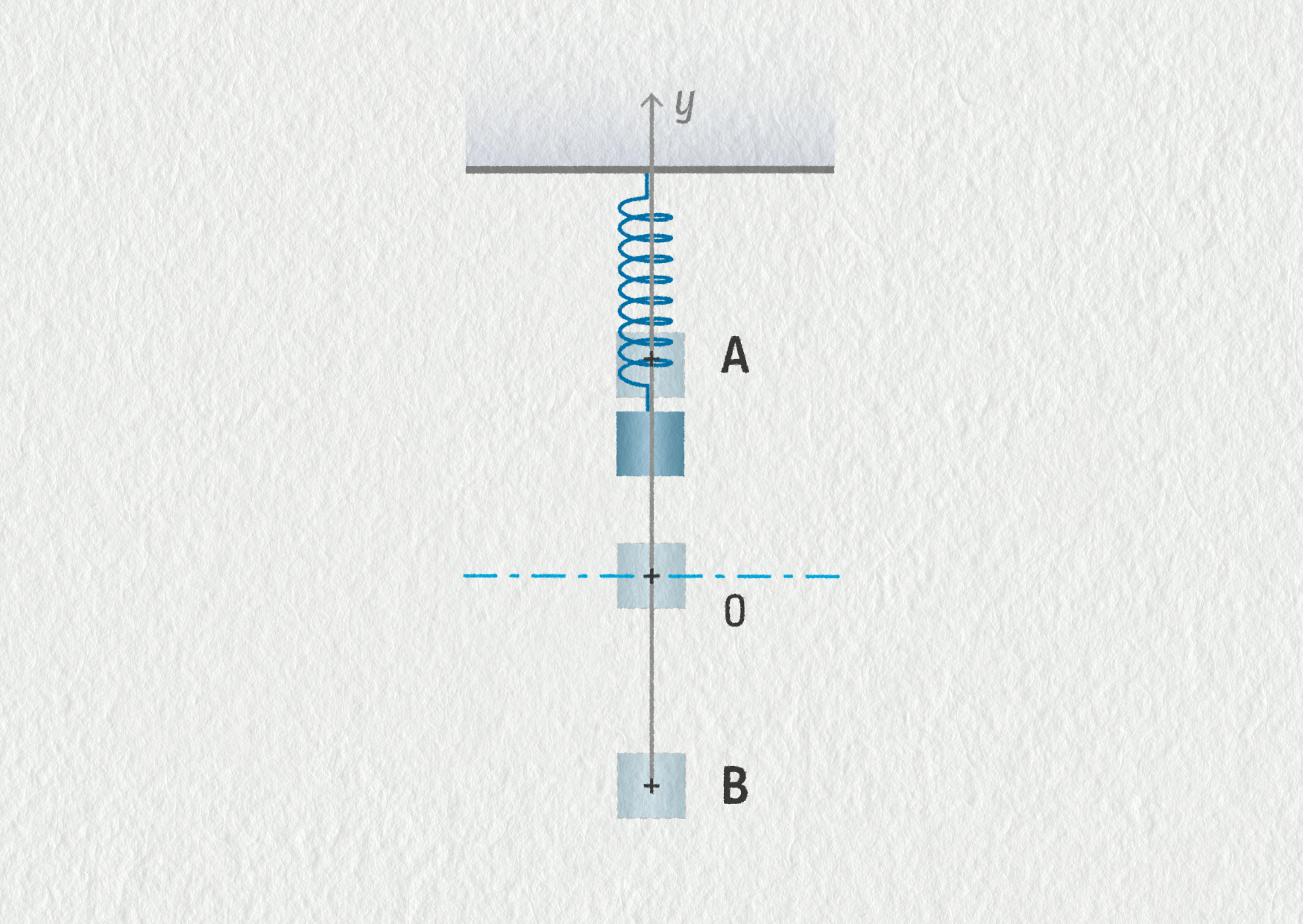
V obrázku 21.13 jsme na trajektorii kmitajícího tělesa vyznačili rovnovážnou polohu O a body obratu A a B. Rozhodněte, ve kterém bodě platí následující tvrzení. Do políček zapište velká písmena (bez dalších znaků).
Zdroj
Kromě polohy patří mezi kinematické veličiny rychlost a zrychlení. Jak závisí na čase tyto veličiny u kmitavého pohybu harmonického oscilátoru? Experimentálně je můžeme získat opět pomocí sonaru v uspořádání na obrázku 21.9. Jelikož je tento pohyb svislý, má smysl uvažovat pouze svislou, tedy y-ovou složku rychlosti \(v_y\) a y-ovou složku zrychlení \(a_y\), neboť ostatní složky jsou trvale nulové.
Zdroj
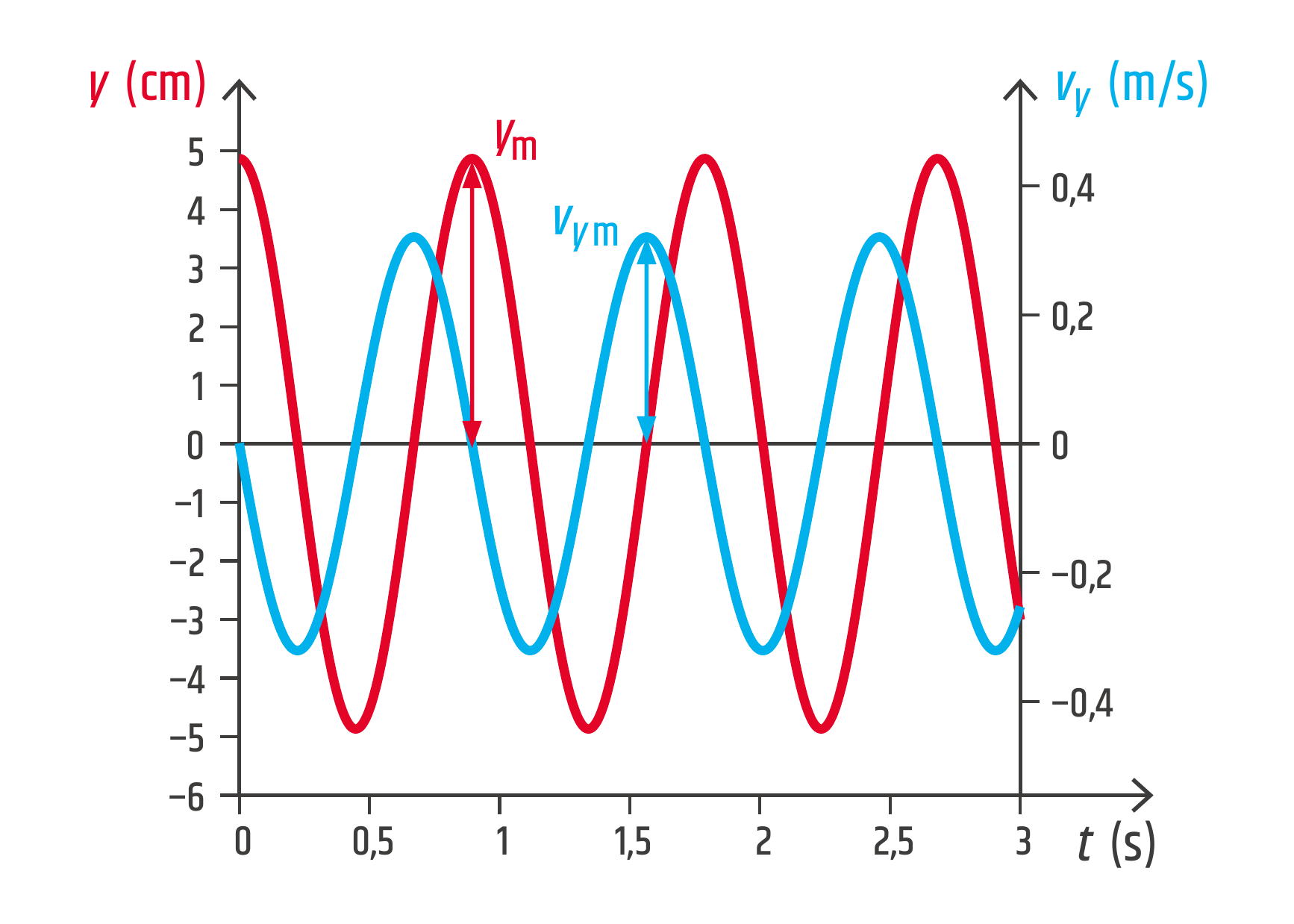
V grafu 21.14 je pro porovnání zobrazena závislost výchylky na čase \(y(t)\) (červená křivka) a závislost svislé složky rychlosti na čase \(v_y(t)\) (modrá křivka).
Vidíme, že u harmonického oscilátoru i rychlost kmitá harmonicky – grafem \(v_y(t)\) je sinusoida. Obě křivky mají stejnou periodu, v našem případě přibližně \(T=0{,}9\ \mathrm{s}\), a jsou vůči sobě posunuty o čtvrt periody. Všimněte si, že v okamžiku, kdy je výchylka maximální (bod obratu), je rychlost nulová. Při průchodu rovnovážnou polohou – tedy v okamžiku, kdy je výchylka nulová – je rychlost maximální.
Maximální velikost rychlosti \(v_{y\mathrm{m}}\) se nazývá amplituda rychlosti. Lze odvodit, že \(v_{y\mathrm{m}}=\omega y_\mathrm{m}\), kde \(\omega\) je úhlová frekvence a \(y_\mathrm{m}\) amplituda výchylky.
Při odečítání amplitud z tohoto grafu musíme zpozornět: výchylka a rychlost jsou dvě různé veličiny, mají jiné jednotky a jejich amplitudy nelze porovnávat. Amplitudu výchylky přečteme pomocí měřítka na levé ose (\(y_\mathrm{m}=5\ \mathrm{cm}\)), amplitudu rychlosti pak pomocí měřítka na ose vpravo (\(v_{y\mathrm{m}}=0{,}35\ \mathrm{m/s}\)).
S pomocí periody \(T=0{,}9\ \mathrm{s}\) vyčtené z grafu se můžeme přesvědčit, že skutečně
\[ v_{y\mathrm{m}}=\omega y_\mathrm{m} = \frac{2\pi}Ty_\mathrm{m} = \frac{2\pi}{0{,}9\ \mathrm{s}}\cdot0{,}05\ \mathrm{m} = 0{,}35\ \mathrm{m/s} \]Souřadnice \(y\) je kladná, když se těleso nachází v kladné části osy \(y\).
Tvrzení e) není správně. Okamžitá rychlost \(\Vec{v}\) je vektorová veličina, má směr (ukazuje směr pohybu) a velikost (kladná hodnota v m/s). Složky rychlosti \(v_x\), \(v_y\) a \(v_z\) říkají, jak moc „šipka“ \(\Vec{v}\) ukazuje ve směru osy \(x\), \(y\) a \(z\). Pokud \(\Vec{v}\) směřuje proti ose \(y\), pohybuje se těleso proti směru osy \(y\) (v našem případě dolů) a \(v_y\) je záporné. Nezaměňujme rychlost \(\Vec{v}\) (vektorová veličina), velikost rychlosti \(v\) (vždy kladná) a svislou složku rychlosti \(v_y\).
Podobně jako pro rychlost můžeme na základě experimentálního záznamu kmitání naší modelové soustavy na fotografii 21.9 zobrazit i závislost zrychlení na čase.

Zdroj
V grafu 21.15 je pro porovnání zobrazena závislost výchylky na čase \(y(t)\) (červená křivka) a závislost svislé složky zrychlení na čase \(a_y(t)\) (zelená křivka).
Křivka zrychlení \(a_y(t)\) má v případě harmonického oscilátoru opět sinusový průběh. Výchylka i svislá složka zrychlení mají stejnou periodu. Křivky jsou vzájemně posunuty o polovinu periody: v okamžiku, kdy \(y(t)\) dosahuje svého maxima (těleso je na své trajektorii nejvýše), má \(a_y(t)\) minimum (těleso zrychluje nejvíce, a to směrem dolů). Obecně lze říci, že zrychlení dosahuje své maximální hodnoty \(a_{y\mathrm{m}}\), právě když je těleso nejdále z rovnovážné polohy. Dá se ukázat, že pro amplitudu zrychlení \(a_{y\mathrm{m}}\) platí
\[ a_{y\mathrm{m}} = \omega^2y_\mathrm{m}\;, \]kde \(\omega\) je úhlová frekvence a \(y_\mathrm{m}\) amplituda výchylky.
V obrázku 21.16 jsme na trajektorii kmitajícího tělesa vyznačili rovnovážnou polohu O a body obratu A a B. Rozhodněte, ve kterém bodě platí následující tvrzení. Do políček zapište velká písmena (bez dalších znaků).

Zdroj
Harmonickou závislost výchylky na čase \(y(t)=y_\mathrm{m}\sin(\omega t+\varphi_0)\) pro pružinový oscilátor s lineární odezvou lze odvodit z druhého Newtonova zákona. V tuto chvíli vezměme tento vztah jako experimentální fakt.
Z něj nyní odvodíme vztahy pro \(y\)-ové složky rychlosti a zrychlení.
Rychlost je derivací polohy podle času. Pro svislé složky platí
\[ v_y = \frac{\mathrm{d}y}{\mathrm{d}t}\;. \]Funkci \(y(t)\) tedy musíme zderivovat podle času (derivujeme složenou funkci):
\[ v_y = \frac{\mathrm{d}y}{\mathrm{d}t} = \frac{\mathrm{d}\bigl(y_\mathrm{m}\sin(\omega t+\varphi_0)\bigr)}{\mathrm{d}t} = y_\mathrm{m}\frac{\mathrm{d}\bigl(\sin(\omega t+\varphi_0)\bigr)}{\mathrm{d}t} = \omega y_m\cos(\omega t+\varphi_0)\;. \]Amplituda rychlosti je tedy skutečně \(v_{y\mathrm{m}}=\omega y_\mathrm{m}\). Funkce \(\cos\) je vůči funkci \(\sin\) posunuta o π/2 radiánů, tedy o čtvrt periody.
Zrychlení je derivací rychlosti podle času. Pro svislé složky platí
\[ a_y = \frac{\mathrm{d}v_y}{\mathrm{d}t}\;. \]Předchozí výsledek \(v_y(t)\) tedy zderivujeme ještě jednou (opět složená funkce):
\[ a_y = \frac{\mathrm{d}v_y}{\mathrm{d}t} = \frac{\mathrm{d}\bigl(\omega y_\mathrm{m}\cos(\omega t+\varphi_0)\bigr)}{\mathrm{d}t} = \omega y_\mathrm{m}\frac{\mathrm{d}\bigl(\cos(\omega t+\varphi_0)\bigr)}{\mathrm{d}t} = -\omega^2y_m\sin(\omega t+\varphi_0)\;. \]Amplituda zrychlení je tedy skutečně \(a_{y\mathrm{m}}=\omega^2y_\mathrm{m}\). Funkce \(-\sin(x)\) je vůči funkci \(\sin(x)\) posunuta o π radiánů, tedy o polovinu periody.

