Obecné vlastnosti
Co je to radioaktivita?
Radioaktivita je fyzikální děj spočívající v samovolné přeměně nestabilního jádra na jiné jádro, která je doprovázena vyzářením vysokoenergetické částice.
Radioaktivní přeměny jsou:
- samovolné – nestabilní jádro nepotřebuje ke své přeměně žádný vnější podnět, přeměna je důsledkem vnitřní nestability (dané kvantovými procesy),
- náhodné – nelze předpovědět okamžik, kdy dojde k přeměně daného jádra; pravděpodobnost přeměny se s časem nezvyšuje ani neklesá, nestabilní jádro „nestárne“,
- nezávislé na vnějších podmínkách – pravděpodobnost přeměny nelze změnit tlakem, teplotou ani chemickými vazbami; přeměnu nestabilního jádra nelze vyvolat ani jí nelze zabránit.
V přírodě existuje přes 80 radioaktivních nuklidů, dalších přes 3 000 radioaktivních nuklidů bylo připraveno uměle.
Radioaktivitu objevil v roce 1896 Henri Becquerel při studiu fluorescence uranových solí. O objasnění její podstaty se zasloužili manželé Pierre Curie a Marie Curie–Skłodowska. Všichni tři obdrželi v roce 1903 Nobelovu cenu.
Veličiny, které se zachovávají
Přestože nedokážeme ovlivnit ani předpovědět okamžik, kdy dojde k radioaktivní přeměně vybraného jádra, je výsledek přeměny dobře předvídatelný. Vodítkem nám jsou veličiny, které se při radioaktivních přeměnách zachovávají:
- elektrický náboj,
- nukleonové číslo,
- energie.
Nejen při dějích v elektrických obvodech, ale i při jaderných dějích se zachovává elektrický náboj. Prakticky to znamená, že protonové číslo nestabilního jádra je rovno součtu protonových čísel jádra a částic, které přeměnou vznikají.
Podobně je to i s počtem nukleonů: nukleonové číslo nestabilního jádra je rovno součtu nukleonových čísel jádra a částic, které přeměnou vznikají.
Zachování energie je pověstnou červenou nití, která se táhne celou fyzikou, jaderné děje nejsou výjimkou. Klidová energie původního nestabilního jádra \(E_{0\mathrm{j}}\) je rovna součtu klidových energií produktů přeměny \(E_{0\mathrm{prod}}\) a uvolněné energie \(E_\mathrm{u}\). Zapsáno rovnicí
\[ E_{0\mathrm{j}} = E_{0\mathrm{prod}} + E_\mathrm{u}\;. \]Uvolněná energie je odnášena produkty přeměny nejčastěji v podobě jejich kinetické energie nebo v podobě elektromagnetického záření.
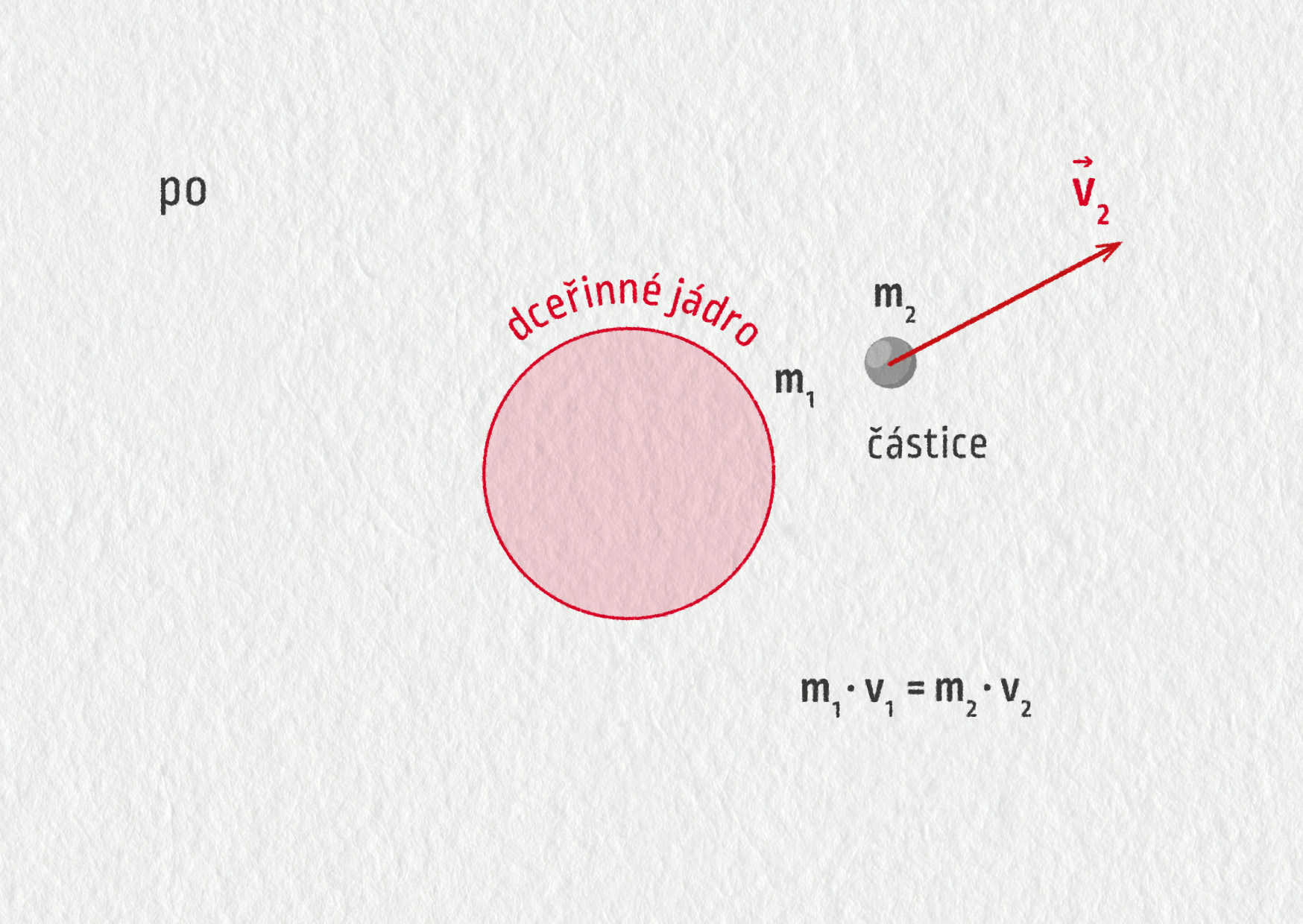
Hybnost je další snadno pochopitelná veličina, která se při jaderných reakcích zachovává. Hybnost částice \(\Vec{p}\) je definována jako součin její hmotnosti a rychlosti, tedy \(\Vec{p}=m\Vec{v}\). Zachování hybnosti znamená, že hybnost původního nestabilního jádra je rovna součtu hybností produktů přeměny. Vztažnou soustavu spojíme s nestabilním jádrem – viz obrázek 27.12, takže počáteční hybnost je \(p=0\ \mathrm{kg}\cdot\mathrm{m/s}\). Přemění-li se toto jádro na dceřiné jádro (hmotnost \(m_1\)) a vyzáří-li při tom lehkou částici (hmotnost \(m_2\)), musí být hybnosti těchto dvou produktů stejně velké a opačného směru,
\[ m_1\Vec{v}_1 + m_2\Vec{v}_2 = \Vec{0} \quad\Rightarrow\quad m_1v_1 = m_2v_2\;. \]Proto je poměr rychlostí produktů přeměny roven převrácenému poměru jejich hmotností, tedy
\[ \frac{v_2}{v_1} = \frac{m_1}{m_2}\;. \]Protože je kinetická energie podle klasické fyziky úměrná druhé mocnině rychlosti, odnáší lehká částice převážnou část uvolněné energie při reakci.

Zdroj
Druhy radioaktivní přeměny
Přeměna α
Přeměna α, nazývaná též α-rozpad, nastává u těžkých jader. Z původního nestabilního jádra je vyzářena α částice, což je jádro helia \({}^4_2\mathrm{He}\). Tímto typem rozpadu se přeměňuje například radioaktivní prvek radium na radon:
\[ {}^{226}_{\hphantom{0}88}\mathrm{Ra} \to {}^{222}_{\hphantom{0}86}\mathrm{Rn} + {}^4_2\mathrm{He}\;. \]Radon je též α zářičem a přeměňuje se na polonium:
\[ {}^{222}_{\hphantom{0}86}\mathrm{Rn} \to {}^{218}_{\hphantom{0}84}\mathrm{Po} + {}^4_2\mathrm{He}\;. \]Obecně můžeme α rozpad vyjádřit rovnicí
\[ {}^A_ZX \stackrel{\alpha}{\longrightarrow} {}^{A-4}_{Z-2}Y + {}^4_2\mathrm{He}\;. \]Proud α částic vycházející z radioaktivního nuklidu, neboli α záření, má velké ionizační účinky, ale špatně proniká látkami. Ochrání nás před ním několikacentimetrová vrstva vzduchu nebo obyčejný list papíru. Nebezpečí hrozí, pokud se zářič dostane do kontaktu s lidským tělem, například při vdechnutí plynného radonu. Účinkům záření na lidský organismus je věnován samostatný oddíl.
Přeměna β−
Tento typ rozpadu nastává u jader, která jsou nestabilní v důsledku příliš velkého počtu neutronů. V původním jádru dojde k přeměně neutronu na proton a současně se při tom uvolní elektron, tj. β− částice, a antineutrino \({}^0_0\bar\nu\). Příkladem rozpadu β− je přeměna radioaktivního izotopu uhlíku 14 na dusík:
\[ {}^{14}_{\hphantom{0}6}\mathrm{C} \to {}^{14}_{\hphantom{0}7}\mathrm{N} + {}^{\hphantom{-}0}_{-1}\mathrm{e} + {}^0_0\bar\nu\;. \]Obecně můžeme β− rozpad vyjádřit rovnicí
\[ {}^A_ZX \stackrel{\beta^-}{\longrightarrow} {}^{\hphantom{1+{}}A}_{Z+1}Y + {}^{\hphantom{-}0}_{-1}\mathrm{e} + {}^0_0\bar\nu\;. \]Proud elektronů, neboli β− záření, proniká hmotou lépe než α záření, ale má menší ionizační účinky. Beta záření je odstíněno několik milimetrů silnou vrstvou kovu.
Fyzikové se studiem rozpadů β− intenzivně zabývali v první třetině 20. století. Podle zákona zachování energie by kinetická energie emitovaných elektronů měla být rovna uvolněné energii při reakci (jediná hodnota, dána přesně rozdílem klidových energií původního jádra a produktů). Ve skutečnosti ovšem zjistili, že spektrum energií emitovaných elektronů je spojité. Byl tak objeven děj, při kterém se energie nezachovává?
Ve 30. letech přišli Wolfgang Pauli a Enrico Fermi se správným vysvětlením. Kromě elektronu totiž beta zářič emituje ještě velmi lehkou neutrální částici, kterou nazvali „neutrino“. Tato částice odnáší chybějící část uvolněné energie.
Neutrino slabě interaguje s hmotou, proto o něm dosud víme velice málo. Poprvé bylo detekováno až v roce 1956. Hmotnost neutrin je o několik řádů menší než hmotnost elektronu, ale je nenulová. Neutrina se pohybují prostorem téměř rychlostí světla. Běžná struktura hmoty je pro ně příliš „řídká“, takže Zemí proletí asi tak snadno, jako proniká nůž krupičnou kaší, reakce s hmotnými částicemi jsou málo pravděpodobné.
Vzhledem k tomu, že při termojaderné syntéze vodíku na hélium ve hvězdách vzniknou dvě neutrina na každé nové jádro hélia, musí být náš vesmír neutriny přímo zaplaven. Obrovské množství neutrin je tak jednou z hypotéz vysvětlujících existenci temné hmoty vesmíru – hmoty, která nezáří, ale má gravitační účinky.
Antineutrino \({}^0_0\bar\nu\) a neutrino \({}^0_0\nu\) mají stejné vlastnosti, liší se pouze znaménkem leptonového čísla.

Zdroj
Přeměna β+
Přeměna β+ nastává u jader, která jsou nestabilní v důsledku přebytku protonů. V původním jádru dojde k přeměně protonu na neutron a současně se při tom uvolní pozitron \({}^0_1\mathrm{e}\) a neutrino \(\nu. \) Příkladem rozpadu β+ je přeměna uměle připraveného radioaktivního izotopu fosforu 30 na křemík (první pozorovaný β+ rozpad, Nobelova cena pro manžele Frédérika a Irène Joliot-Curie)::
\[ {}^{30}_{15}\mathrm{P} \to {}^{30}_{14}\mathrm{Si} + {}^0_1\mathrm{e} + {}^0_0\nu\;. \]Obecně můžeme β+ rozpad vyjádřit rovnicí
\[ {}^A_ZX \stackrel{\beta^+}{\longrightarrow} {}^{\hphantom{1-{}}A}_{Z-1}Y + {}^0_1\mathrm{e} + {}^0_0\nu\;. \]Pozitrony okamžitě po svém vzniku reagují s běžnými elektrony, přičemž vzniká elektromagnetické záření o přesně dané frekvenci. Této vlastnosti využívá lékařská zobrazovací metoda PET (pozitronové emisní tomografie).
Pozitron je antičástice elektronu. K tomu, že by v přírodě mohly kromě normálních částic existovat také jejich „dvojníci“ (antičástice) s opačným znaménkem náboje, teoreticky dospěl v roce 1928 Paul Dirac. O tři roky později první takové částice objevil Carl David Anderson při studiu kosmického záření.
Částice a odpovídající antičástice mají přesně stejnou hmotnost a opačné znaménko náboje.
Pozitron je antičásticí elektronu – má stejnou hmotnost jako elektron a nese kladný náboj (tj. elementární náboj +1,602 ⋅ 10−19 C). Podobně antiproton má hmotnost rovnou hmotnosti protonu a nese záporný náboj. Částice s nulovým nábojem (neutron, neutrino) jsou samy sobě antičásticí.
Vesmír vytvořený z antihmoty by fungoval úplně stejně jako náš vesmír tvořený hmotou. Platily by zde stejné fyzikální zákony. Například antivodík by byl tvořen záporným jádrem (antiprotonem), kolem něhož by obíhal kladný pozitron. Energiové hladiny, a tím pádem i emitované spektrum, by byly stejné jako u normálního vodíku. Odkud tedy víme, že v našem vesmíru převládá hmota nad antihmotou?
Pokud se k sobě částice a její antičástice dostatečně přiblíží, dochází k anihilaci hmoty. Obě tyto částice přestávají existovat, ale jejich energie nezaniká a projeví se vznikem dvou fotonů o stejné frekvenci šířících se opačnými směry. Anihilace je tedy přímá přeměna látky na záření. Při anihilaci se zachovává celkový elektrický náboj, celková hybnost, celková energie. Zachování energie při anihilaci elektronu s pozitronem zapíšeme rovnicí
\[ m_\mathrm{e}c^2 + m_\mathrm{e}c^2 = 2hf\;, \]odkud můžeme vypočítat frekvenci vzniklého záření \(f=1{,}24\cdot10^{20}\ \mathrm{Hz}\). Zákon zachování hybnosti zaručuje totožnou frekvenci a šíření fotonů opačnými směry.

Zdroj
Kdyby v našem vesmíru existovaly galaxie tvořené antihmotou, nutně by na jejich okrajích vznikalo intenzivní záření o charakteristické frekvenci, které bychom na Zemi mohli detekovat. Nic podobného ovšem nepozorujeme, a proto usuzujeme, že antihmota je ve vesmíru velice vzácná a rozhodně netvoří rozlehlé oblasti.
Zvláštním případem radioaktivní přeměny je elektronový záchyt. Nejedná se zde o rozpad v pravém slova smyslu.
Jádro s přebytkem protonů s určitou pravděpodobností zachytí elektron z nejnižší slupky K elektronového obalu. Na uvolněné místo se pak přesune elektron z některé vyšší hladiny a při tom vyzáří foton o charakteristické frekvenci. Příkladem je přeměna americia na plutonium
\[ {}^{240}_{\hphantom{0}95}\mathrm{Am}^* + {}^{\hphantom{-}0}_{-1}\mathrm{e} \stackrel{\varepsilon}{\longrightarrow} {}^{240}_{\hphantom{0}94}\mathrm{Pu} + {}^0_0\nu\;. \]Přeměna γ
Přeměna γ spočívá ve vyzáření vysokoenergetického fotonu z původního jádra. Počet protonů ani neutronů se nemění, jádro se pouze zbavuje přebytečné energie. V praxi využívaným zdrojem γ záření je americium 241
\[ {}^{241}_{\hphantom{0}95}\mathrm{Am}^* \to {}^{241}_{\hphantom{0}94}\mathrm{Am} + \gamma\;. \]kde jsme hvězdičkou vyznačili, že jádro je v excitovaném (energeticky bohatém) stavu.
Gama záření má ionizační účinky a výborně proniká hmotou. Odstínit je můžeme vrstvou těžkého kovu, například olova.
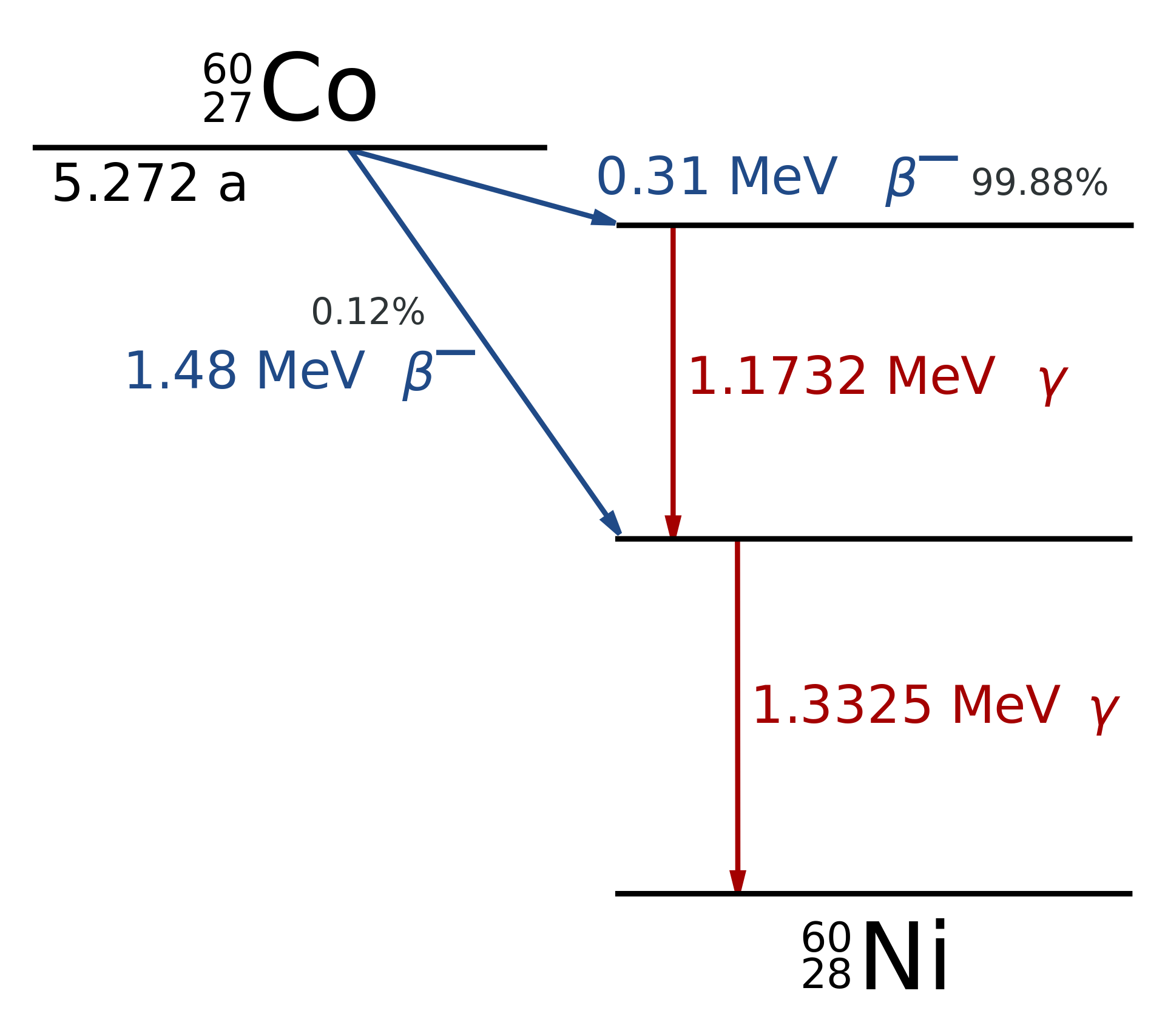
Podobně jako energie elektronů v atomovém obalu může nabývat jen některých hodnot (energiové hladiny – viz kapitola 25), je kvantována i energie jader. Při přeměně α nebo β se může stát, že dceřiné jádro nebude v nejnižším energetickém stavu (základní stav, nejstabilnější), ale ocitne se na některé vyšší energiové hladině (excitovaný stav, nestabilní). Toto excitované jádro má tendenci samovolně přejít do stabilnějšího stavu (na nižší energiovou hladinu). Odpovídající energie se při tom zbaví vyzářením γ fotonu, čili elektromagnetického záření o vysoké frekvenci.
Zdroj
Gama fotony mají nulovou klidovou hmotnost, nulový elektrický náboj, pohybují se přesně rychlostí světla ve vakuu \(c\) a jejich energii vypočítáme podle vztahu
\[ E_\gamma = hf\;, \]kde \(h=6{,}626\cdot10^{-34}\ \mathrm{J}\cdot\mathrm{s}\) je Planckova konstanta a \(f\) je frekvence odpovídající elektromagnetické vlny.
Zákon radioaktivní přeměny
Přestože okamžik přeměny jediného radioaktivního jádra nelze určit, statisticky velký soubor takových jader vykazuje zcela předvídatelné chování. Popisuje je zákon radioaktivní přeměny.
Zdroj
Symbolem \(N(t)\) označíme počet jader radioaktivního nuklidu ve zkoumaném vzorku v určitém čase \(t\). Jejich počet na začátku pozorování označíme \(N_0\), tedy \(N_0=N(t=0\ \mathrm{s})\).
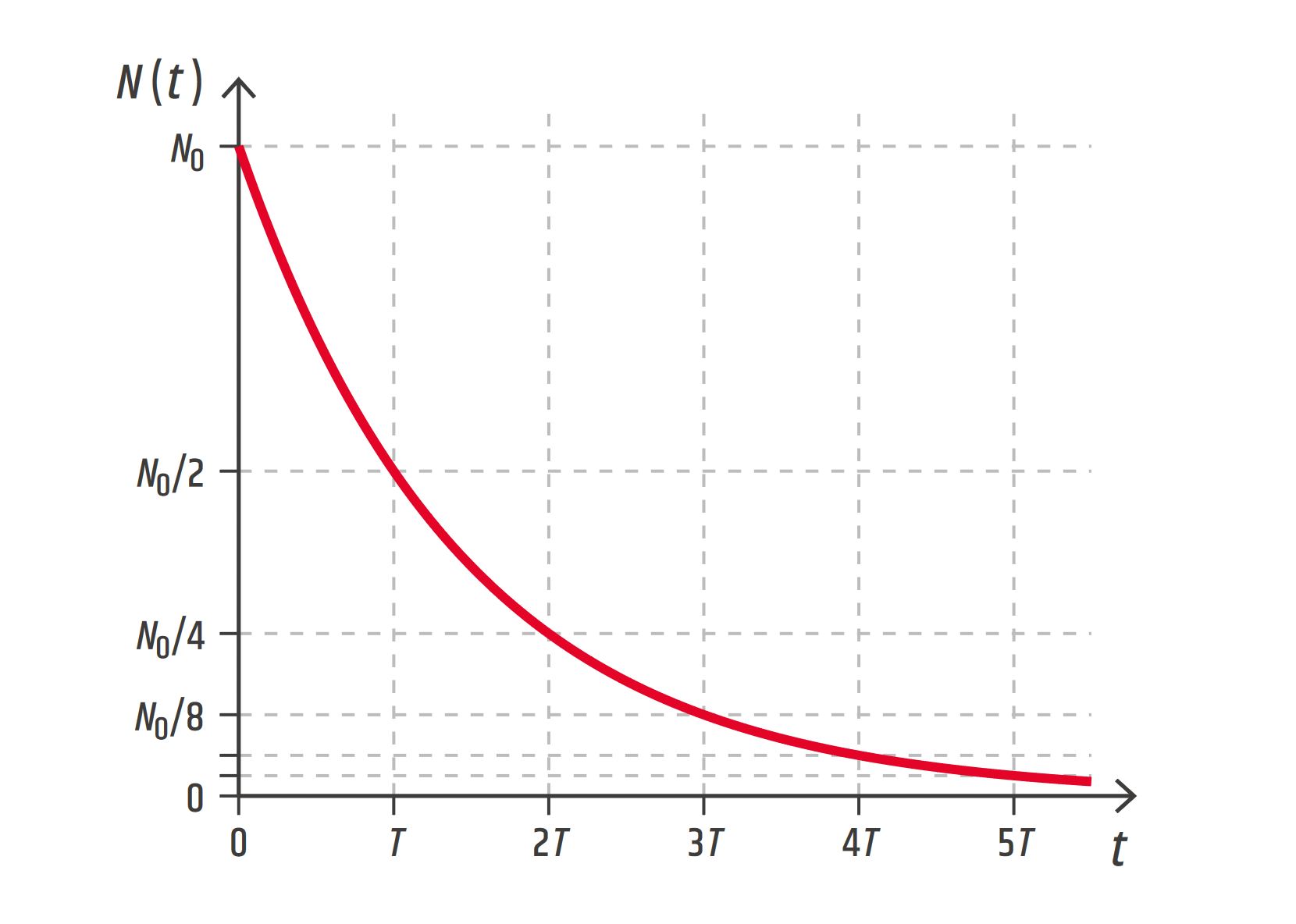
Jádra se postupem času náhodně rozpadají, takže jejich počet klesá, \(N(t)\) je klesající funkcí času. I ve zcela slabě zářících vzorcích je počet radioaktivních jader obrovský (například 1010) a funkce \(N(t)\) odpovídá hladké exponenciální křivce – viz obrázek 27.16. Jejím matematickým vyjádřením je zákon radioaktivní přeměny.
Zákon radioaktivní přeměny
\[ N(t) = N_0\mathrm{e}^{-\lambda t} \]\(N(t)\) – počet radioaktivních jader v čase \(t\)
\(N_0\) – počet radioaktivních jader na začátku pozorování
\(\lambda\) – přeměnová konstanta
V zákoně radioaktivní přeměny vystupuje materiálová konstanta \(\lambda\), zvaná přeměnová (nebo též rozpadová) konstanta. Vyjadřuje pravděpodobnost rozpadu jednoho jádra daného nuklidu za časovou jednotku. Její základní jednotkou je tedy s−1. Velmi nestabilní jádra se vyznačují vysokou hodnotou konstanty \(\lambda\).
Exponenciála na obrázku 27.16 má jednu zajímavou vlastnost: po uplynutí doby \(T\) se počet radioaktivních jader sníží na polovinu původního počtu, po uplynutí další stejně velké doby \(T\) se počet \(N\) sníží opět na polovinu (tedy na čtvrtinu původního počtu) atd. Jinými slovy, ať zahájíme pozorování v jakýkoliv okamžik, počet radioaktivních jader poklesne na polovinu původního počtu vždy za stejnou dobu \(T\). Tato doba se nazývá poločas radioaktivní přeměny, někdy též poločas rozpadu.
Poločas radioaktivní přeměny \(T\) je doba, za kterou poklesne počet radioaktivních jader na polovinu. Platí
\[ T = \frac{\ln2}{\lambda}\;. \]Podle definice se za čas \(t=T\) sníží počet radioaktivních jader na polovinu původního počtu,
\[ N(t=T) = \frac{N_0}2\;. \]Dosadíme za čas \(t=T\) do zákona radioaktivní přeměny:
\[\begin{aligned} N(T) &= N_0\mathrm{e}^{-\lambda T}\\ \frac{N_0}2 &= N_0\mathrm{e}^{-\lambda T}\\ \end{aligned}\]Rovnici vydělíme \(N_0\) a zlogaritmujeme:
\[\begin{aligned} \frac12 &= \mathrm{e}^{-\lambda T}\\ -\ln2 &= -\lambda T\\ \end{aligned}\]Odtud plyne hledaný vztah pro poločas přeměny
\[ T = \frac{\ln2}{\lambda}\;. \]| Nuklid | Typ přeměny | Poločas přeměny |
|---|---|---|
| \({}^{238}\mathrm{U}\) | α | 4,47 ⋅ 109 let |
| \({}^{40}\mathrm{K}\) | β− | 1,25 ⋅ 109 let |
| \({}^{14}\mathrm{C}\) | β− | 5,73 ⋅ 103 let |
| \({}^{3}\mathrm{H}\) | β− | 12,3 let |
| \({}^{131}\mathrm{I}\) | β− | 8,02 dní |
| \({}^{222}\mathrm{Rn}\) | α | 3,82 dní |
| \({}^{99}\mathrm{Tc}\) | γ | 6,04 h |
Po vyzáření γ fotonu jádro technecia již není radioaktivní. Ptáme se na zbylý počet radioaktivních jader.
Technecium 99 má poločas přeměny 6,04 h.
- Vypočítejte konstantu radioaktivní přeměny.
- O kolik procent se sníží počet radioaktivních jader za tři hodiny?
a) Poločas přeměny je \(T=6{,}04\ \mathrm{h}=2{,}17\cdot10^4\ \mathrm{s}\), takže přeměnová konstanta je
\[ \lambda = \frac{\ln2}T = 3{,}19\cdot10^{-5}\ \mathrm{s}^{-1}\;. \]b) Vztah mezi počtem jader \(N\) a časem \(t\) není ani lineární, ani se nejedná o nepřímou úměrnost. Používání trojčlenky zde není fyzikálně správné, neboť vztah veličin je exponenciální. Musíme aplikovat zákon radioaktivní přeměny.
\[\begin{aligned} t &= 3{,}00\ \mathrm{h} = 1{,}08\cdot10^4\ \mathrm{s}\\ N(t) &= N_0\mathrm{e}^{-\lambda T} = N_0\exp(-3{,}19\cdot10^{-5}\ \mathrm{s}^{-1}\cdot1{,}08\cdot10^4\ \mathrm{s}) = 0{,}709N_0\\ \end{aligned}\]Po uplynutí tří hodin ve vzorku zůstává přibližně 71 % procent radioaktivních jader, za tři hodiny se jejich počet sníží o 29 %.
V přírodě se vyskytuje jediný stabilní izotop jódu \({}^{127}\mathrm{I}\). Pro lidský organismus je jód nezbytný k syntéze hormonů. Je obsažen v mořské soli a mořských rybách.
Radioaktivní izotop jódu \({}^{131}\mathrm{I}\) vzniká při štěpení uranu. Do životního prostředí se může dostat při výbuchu jaderné bomby nebo při výbuchu jaderného reaktoru. Poněvadž mají oba izotopy stejné chemické vlastnosti, lidské tělo nepozná „zdravý“ jód od „škodlivého“ a při akumulaci izotopu 131 ve štítné žláze hrozí její ozáření s rizikem následné rakoviny.
- Vysvětlete, k čemu slouží jodové tablety? Má smysl je užívat preventivně?
- Vypočítejte přeměnovou konstantu izotopu 131.
- Vypočítejte, za jak dlouho se 99 % radioaktivního jódu rozpadne.

Zdroj
a) Jodové tablety obsahují stabilní izotop 127. V případě jaderné havárie, nejlépe do jedné hodiny po vzniku nebezpečí, by dospělí měli užít dvě tablety. Tím se lidské tělo na několik dní zasytí „zdravým“ jódem, takže žádný další jód již nepřijímá. Nemá smysl překračovat dávkování – nadbytečné množství se vyloučí, ani užívat tablety, pokud se do prostředí nedostal radioaktivní jód – hrozí poškození štítné žlázy.
b) Poločas přeměny je \(T=8{,}02\ \hbox{dne}=6{,}93\cdot10^5\ \mathrm{s}\). Přeměnová konstanta je
\[ \lambda = \frac{\ln2}T = 1{,}00\cdot10^{-6}\ \mathrm{s}^{-1}\;. \]c) Pokud se 99 % jader rozpadne, zůstává ve vzorku 1 % jader. Počítáme čas \(t_1\), při němž \(N(t_1)=0{,}01N_0\). Dosadíme do zákona radioaktivní přeměny
\[ 0{,}01N_0 = N_0\mathrm{e}^{-\lambda t_1}\;, \]rovnici vydělíme počátečním počtem \(N_0\)
\[ 0{,}01 = \mathrm{e}^{-\lambda t_1} \]a zlogaritmujeme
\[ \ln(0{,}01) = \ln\mathrm{e}^{-\lambda t_1} \]K další úpravě použijeme vlastnosti logaritmů \(\ln a^x=x\ln a\) a \(\ln\mathrm{e}=1\), takže
\[ \ln(0{,}01) = -\lambda t_1\;, \]odkud získáváme hledaný čas
\[ t_1 = -\frac{\ln(0{,}01)}{\lambda} = 4{,}61\cdot10^6\ \mathrm{s}\;. \]99 % jader radioaktivního jódu se rozpadne za 53 dní, čili po dvou měsících zůstává v prostředí méně než 1 % původního radioaktivního jódu.
Zákon radioaktivní přeměny je výborný nástroj k teoretickým předpovědím, ale jak do něj máme získat vstupní údaje? Jak změřit počet radioaktivních jader \(N(t)\)? V jednom gramu kovu je řádově 1022 jader – dá se vůbec experimentálně zjistit, jestli jsou některá z nich nestabilní a kolik těch nestabilních vlastně je?
Aktivita
Radioaktivita je fyzikální děj spočívající v samovolné přeměně nestabilního jádra na jiné jádro, která je doprovázena vyzářením vysokoenergetické částice. A právě tuto vysokoenergetickou částici (α, β nebo γ) dokážeme detekovat. Jsme tedy schopni změřit počet vyzářených částic za sekundu, neboli počet reakcí, které za sekundu proběhnou.
Aktivita vzorku \(A\) je definována jako počet radioaktivních přeměn, které v něm proběhnou za sekundu. Její jednotkou je becquerel Bq. Jeden becquerel odpovídá jedné přeměně za sekundu. K měření aktivity se používá Geigerův–Müllerův detektor.
Aktivita vzorku závisí na počtu přítomných radioaktivních jader \(N\) a pravděpodobnosti \(\lambda\), že se dané jádro za sekundu rozpadne. V každém okamžiku tedy platí vztah přímé úměrnosti
\[ A = \lambda N\;. \]Z něj a ze zákona radioaktivní přeměny vyplývá, že aktivita vzorku klesá s časem exponenciálně a že pojem poločas přeměny \(T\) lze aplikovat i na aktivitu,
\[ A(t) = A_0\mathrm{e}^{-\lambda t}\;. \]Uvažujme radioaktivní látku tvořenou jediným nuklidem. V čase \(t\) se v látce nachází \(N(t)\) radioaktivních jader. Během krátkého časového intervalu \(\mathrm{d}t\) se počet radioaktivních jader sníží na hodnotu \(N(t+\mathrm{d}t)\). Změna počtu jader \(\mathrm{d}N=N(t+\mathrm{d}t)-N(t)\) je zřejmě záporná. Během intervalu \(\mathrm{d}t\) tedy proběhlo \(-\mathrm{d}N\) rozpadů, bylo vyzářeno \(\mathrm{d}N\) vysokoenergetických částic.
Aktivita vzorku \(A\) vyjadřuje počet rozpadů za časovou jednotku, takže
\[ A = \frac{\mathrm{d}N}{\mathrm{d}t}\;. \]Aktivita látky v daný okamžik je záporně vzatou derivací počtu radioaktivních jader.
Pravděpodobnost určitého jevu počítáme jako podíl počtu příznivých případů a počtu případů možných. Během \(\mathrm{d}t\) se rozpadlo \(-\mathrm{d}N\) jader z celkového počtu přítomných jader \(N\), pravděpodobnost rozpadu je \(-\mathrm{d}N/N\). Přeměnová konstanta \(\lambda\) je definována jako pravděpodobnost rozpadu jádra za časovou jednotku, tedy
\[ \lambda = \frac{\displaystyle\;\frac{-\mathrm{d}N}N\;}{\mathrm{d}t} = -\frac{\mathrm{d}N}{\mathrm{d}t} \frac1N\;. \]S využitím definice aktivity můžeme psát
\[ A = \frac{\mathrm{d}N}{\mathrm{d}t} = \lambda N\;. \]Pokud umíte derivovat, můžete ověřit, že exponenciální funkce \(N(t)=N_0\mathrm{e}^{-\lambda t}\) je řešením odvozené diferenciální rovnice
\[ -\frac{\mathrm{d}N}{\mathrm{d}t} = \lambda N\;. \]Svačinka. Buňky živých organismů jsou přibližně ze 20 % tvořeny uhlíkem. V živých organismech připadá na jedno jádro radioaktivního uhlíku \({}^{14}\mathrm{C}\) přibližně 8 ⋅ 1011 stabilních jader uhlíku \({}^{12}\mathrm{C}\). Odhadněte aktivitu stogramové porce zeleniny.

Zdroj
Řešení provedeme ve třech krocích:
- odhadneme počet radioaktivních atomů \(N\) v porci zeleniny,
- vypočítáme konstantu radioaktivní přeměny \(\lambda\) uhlíku \({}^{14}\mathrm{C}\),
- určíme aktivitu \(A\).
1) Ve 100 g zeleniny je přibližně 20 gramů uhlíku. Jeden atom uhlíku 12 má hmotnost \(12\ \mathrm{u}=12\cdot1{,}66\cdot10^{-27}\ \mathrm{kg}=2{,}0\cdot10^{-26}\ \mathrm{kg}\). Ve stogramové porci zeleniny je tedy \(1{,}0\cdot10^{24}\) atomů uhlíku, tedy přibližně \(1{,}3\cdot10^{12}\) radioaktivních jader \({}^{14}\mathrm{C}\).
2) Poločas přeměny je \(T=5\,730\ \mathrm{let}=1{,}81\cdot10^{11}\ \mathrm{s}\), takže konstanta radioaktivní přeměny je
\[ \lambda = \frac{\ln2}T = 3{,}83\cdot10^{-12}\ \mathrm{s}^{-1}\;. \]3) Aktivita porce zeleniny je \(A=\lambda N=3{,}83\cdot10^{-12}\ \mathrm{s}^{-1}\cdot1{,}3\cdot10^{12}\approx5\ \mathrm{Bq}\). Lidské tělo je na tak nízké dávky záření zcela adaptováno.

Zdroj
Určování stáří pomocí radionuklidů
V geologii a archeologii se radioaktivita látek využívá ke zjišťování stáří. Například stáří Země bylo přesně určeno díky radioaktivitě uranu a složení nejstarších vyvřelin (viz cvičení 8).
Na tomto místě vysvětlíme princip nejznámější radiouhlíkové metody.
V přírodě se vyskytují dva stabilní izotopy uhlíku \({}^{12}\mathrm{C}\) (98,9 %) a \({}^{13}\mathrm{C}\) (1,1 %) a radioaktivní izotop \({}^{14}\mathrm{C}\). Jeho poločas přeměny je 5 730 let. Izotop 14 vzniká v horních vrstvách atmosféry při interakci dusíku s kosmickým zářením a radioaktivními procesy se opět rozpadá, takže jeho množství v atmosféře je stálé. Na jedno jádro radioaktivního uhlíku 14 připadá přibližně 8 ⋅ 1011 stabilních jader uhlíku. Rostliny používají uhlík z atmosférického CO2 ke stavbě svých těl. Protože všechny izotopy mají stejné chemické vlastnosti, jsou rostlinami asimilovány stejně snadno. Zastoupení radioizotopu 14 v živých organismech je tedy stejné jako v atmosféře. V okamžiku smrti rostliny ovšem začíná množství uhlíku 14 bez náhrady klesat. Měřením aktivity vzorku \(A\) a aktivity \(A_0\) živé tkáně obsahující stejné množství uhlíku můžeme ze zákona radioaktivní přeměny vypočítat stáří vzorku. Vyzkoušet si to můžete ve cvičení 7.

Zdroj
Jak funguje Geigerův–Müllerův detektor záření?
Zdroj
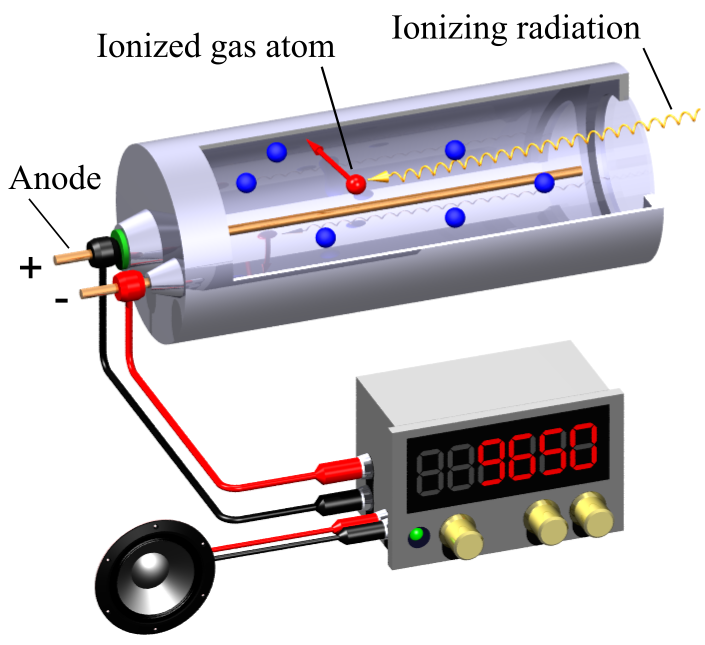
Sonda Geiger–Müllerova detektoru má tvar válce a je tvořena dvěma souosými elektrodami. Prostor mezi elektrodami je vyplněn zředěným plynem. Na elektrody je přivedeno napětí řádově 1 kV. Vysokoenergetická částice uvolněná při jaderné přeměně vstupuje tenkým okénkem a způsobí ionizaci atomů plynu. Vzniklé ionty a uvolněné elektrony jsou elektrickým polem přitahovány k elektrodám, v plynu tak vznikne kratičký elektrický výboj. Jejich dopad na elektrody vyvolá v připojeném elektrickém obvodu kratičký elektrický impulz. Elektronický čítač potom zaznamenává počet elektrických pulzů. Účinnost tohoto detektoru se pohybuje kolem 2 %.
Účinky záření na člověka
Proč je ionizující záření nebezpečné
Během radioaktivních přeměn jsou z daného materiálu do prostředí uvolňovány vysokoenergetické částice α, β nebo γ, které tvoří ionizující záření. Tím, jak se srážejí s atomy a molekulami tohoto prostředí, jim postupně předávají svoji energii. Osamocený atom, který získá energii, je buď excitován (přejde na vyšší energiovou hladinu) nebo přímo ionizován (ztratí elektron). U molekul dochází nejčastěji k přerušení vazeb mezi jejími součástmi. Vznikají tak ionty, které mohou dále reagovat. Pro úplnost poznamenejme, že podobné ionizační účinky má i proud neutronů, proud urychlených protonů a rentgenové záření.
Ionizujícímu záření jsme vystaveni trvale. Jeho nejsilnějšími přirozenými zdroji jsou radioaktivní látky v zemském podloží a záření dopadající z kosmu, které je z velké části odstíněné atmosférou.
Díky záření jsou ve vzduchu stále přítomny nějaké ionty, takže k „zažehnutí“ blesku při bouřce stačí jen dostatečně vysoké napětí mezi zemí a mrakem. Ionizující záření může narušit vazby mezi atomy pevné látky, což vede k radiačnímu křehnutí materiálu.
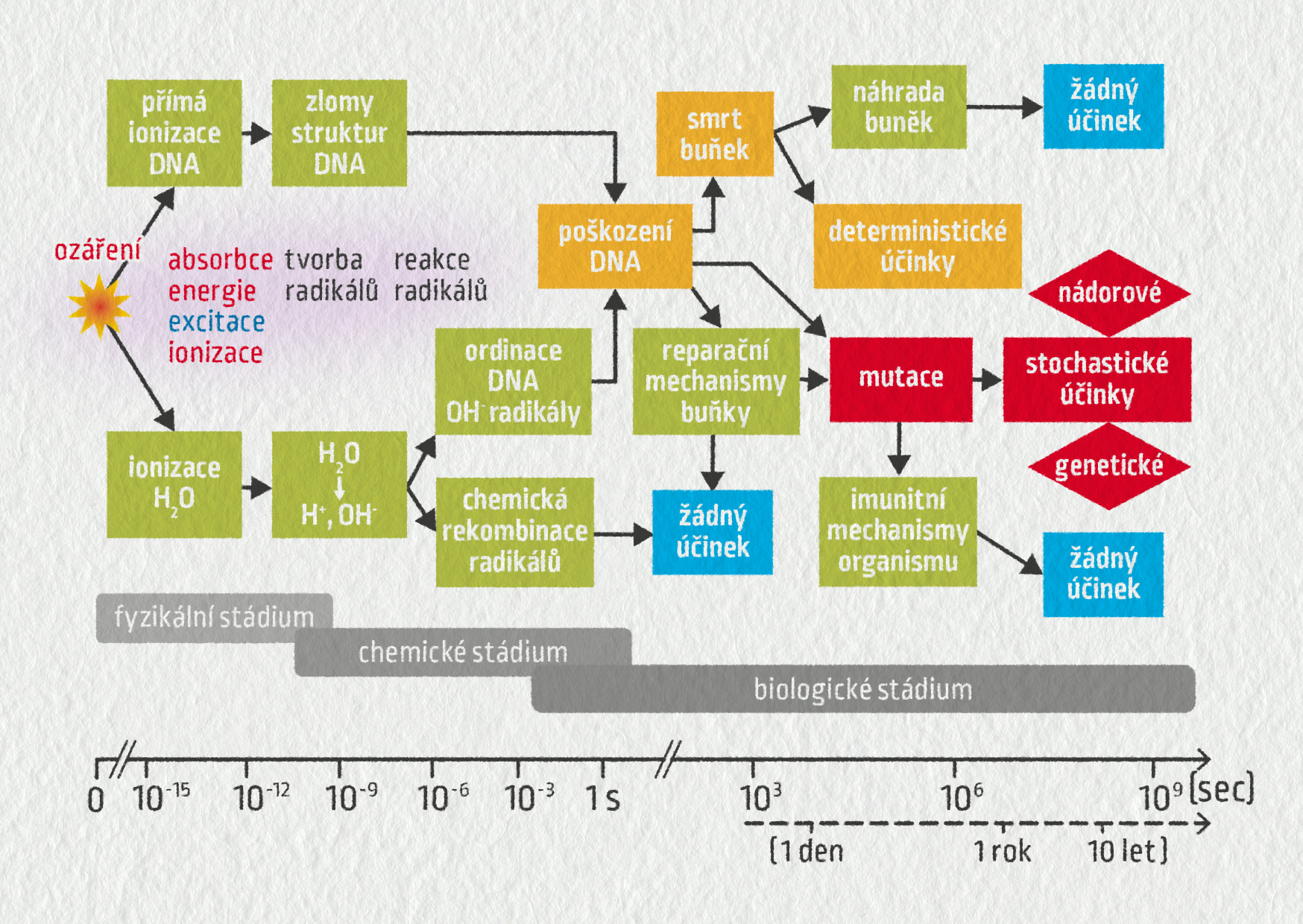
Zdroj
Mnohem závažnější důsledky má ovšem ionizace v živých organismech. Jak známo z biologie, informace o buňce a o způsobu jejího rozmnožování jsou zakódovány v DNA uložené v buněčném jádru. DNA, neboli deoxyribonukleová kyselina, je makromolekula – informace je tedy zakódována chemicky v podobě řetězce nukleotidů.
Ionizující záření, které proletí buňkou, může DNA narušit přímo přerušením některé vazby v řetězci nebo nepřímo vytvořením volných radikálů, které následně poškodí DNA. Malý defekt, například poškození jedné poloviny řetězce DNA, dokáže buňka opravit. Pokud je poškození DNA rozsáhlejší, například na více místech, a buňka je neopraví, nejčastěji zahyne. Odumřelé buňky dokáže tělo nahradit, ale nesmí jich být příliš mnoho na jednom místě, v tom případě dochází k odumření celé tkáně a ztrátě funkce odpovídajícího orgánu.
Poškození, které nepřivodí smrt buňky, vede k její mutaci – odlišnému chování buňky a všech jejích potomků. Jednou z možností je ztráta kontroly nad svou reprodukcí a vznik rakoviny. Imunitní systém člověka si většinou dokáže poradit i se zmutovanými buňkami, ale tato schopnost se s věkem zhoršuje. Ukazuje se, že nízké dávky záření dokáží přímo „nastartovat“ obranyschopnost organismu, takže imunitní systém pak dokáže opravit například poruchy pohybového aparátu. Na tomto principu jsou založeny radonové lázně (první na světě vznikly v Jáchymově v roce 1906).
Poznamenejme, že k poškození buňky a vzniku onemocnění stačí teoreticky jediná ionizující částice (i když je vznik onemocnění extrémně nepravděpodobný). Na nízké dávky záření jsou živé organismy adaptovány a měřitelný vliv mají až výrazně vyšší dávky.
Jak porovnávat účinky záření na živé organismy
Absorbovaná dávka záření \(D\) je rovna energii, kterou získá jeden kilogram hmoty průchodem příslušného záření. Platí vztah
\[ D = \frac{\hbox{absorbovaná energie}}{\hbox{hmotnost}}\;. \]Jednotkou absorbované dávky záření je gray (Gy), 1 Gy = 1 J/kg.
Jednotlivé druhy záření se liší účinky na živé buňky. Velké a těžké jádro helia se v látce chová jako rozjetý kamion v lese: narazí do všech stromů, které mu stojí v cestě, a všechny poškodí, ale brzy se zastaví. Svou kinetickou energii odevzdá do okolí na krátké dráze. Záření α hmotu silně ionizuje, ale je málo pronikavé. Napoak záření β, totiž lehké a malé elektrony, bychom mohli připodobnit k náboji vystřelenému v pušky: dostane se mnohem dál a nezpůsobí v lese takovou paseku. Beta záření méně ionizuje a lépe proniká hmotou.
Biologické účinky jednotlivých druhů záření zohledňuje veličina ekvivalentní dávka záření \(H\). Získáme ji vynásobením absorbované dávky \(D\) radiačním váhovým faktorem \(W_\mathrm{R}\), tedy
\[ H = W_\mathrm{R}D\;, \]kde \(W_\mathrm{R}\) má hodnotu 1 pro β a γ záření, hodnotu 20 pro α záření a hodnotu závislou na rychlosti pro neutrony. Jednotkou ekvivalentní dávky je sievert Sv.
Problematikou měření množství záření a jeho účinků na člověka se zabývá dozimetrie.
Občané žijící v ČR obdrží za rok v průměru dávku 3,2 mSv. Roční limit ozáření z průmyslových zdrojů je pro obyvatelstvo 1 mSv/rok, roční limit pro radiační pracovníky je 20 mSv/rok. V motivační aktivitě si můžete spočítat, jakou ekvivalentní dávku získáte za rok.
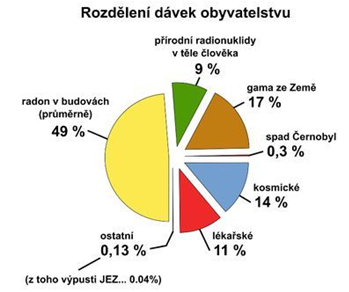
Zdroj
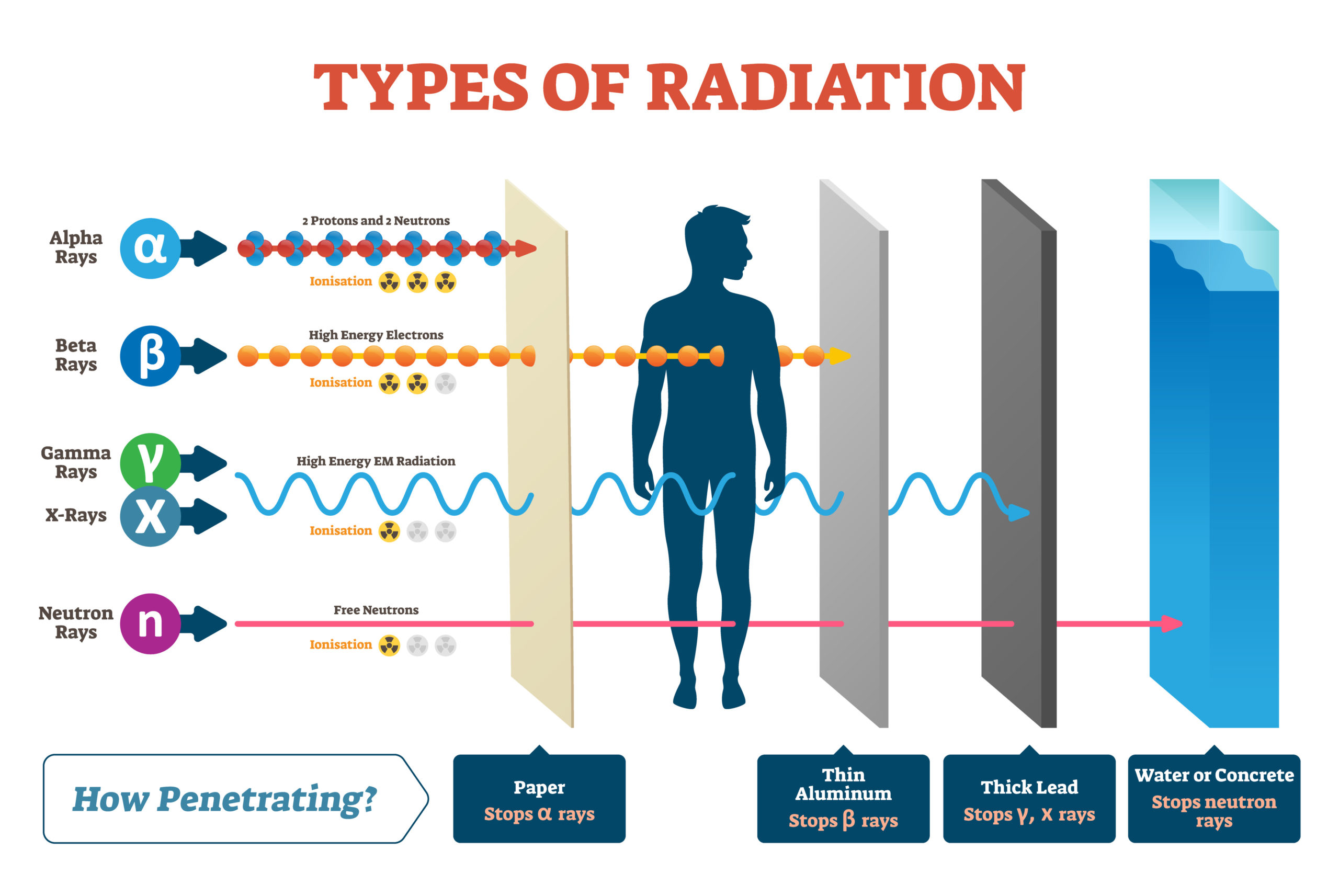
Zdroj

