Polohový vektor a posunutí

Cvičení 1

Určete složky polohových vektorů bodů A, B, C a D.

14.42 – Složky polohových vektorů.
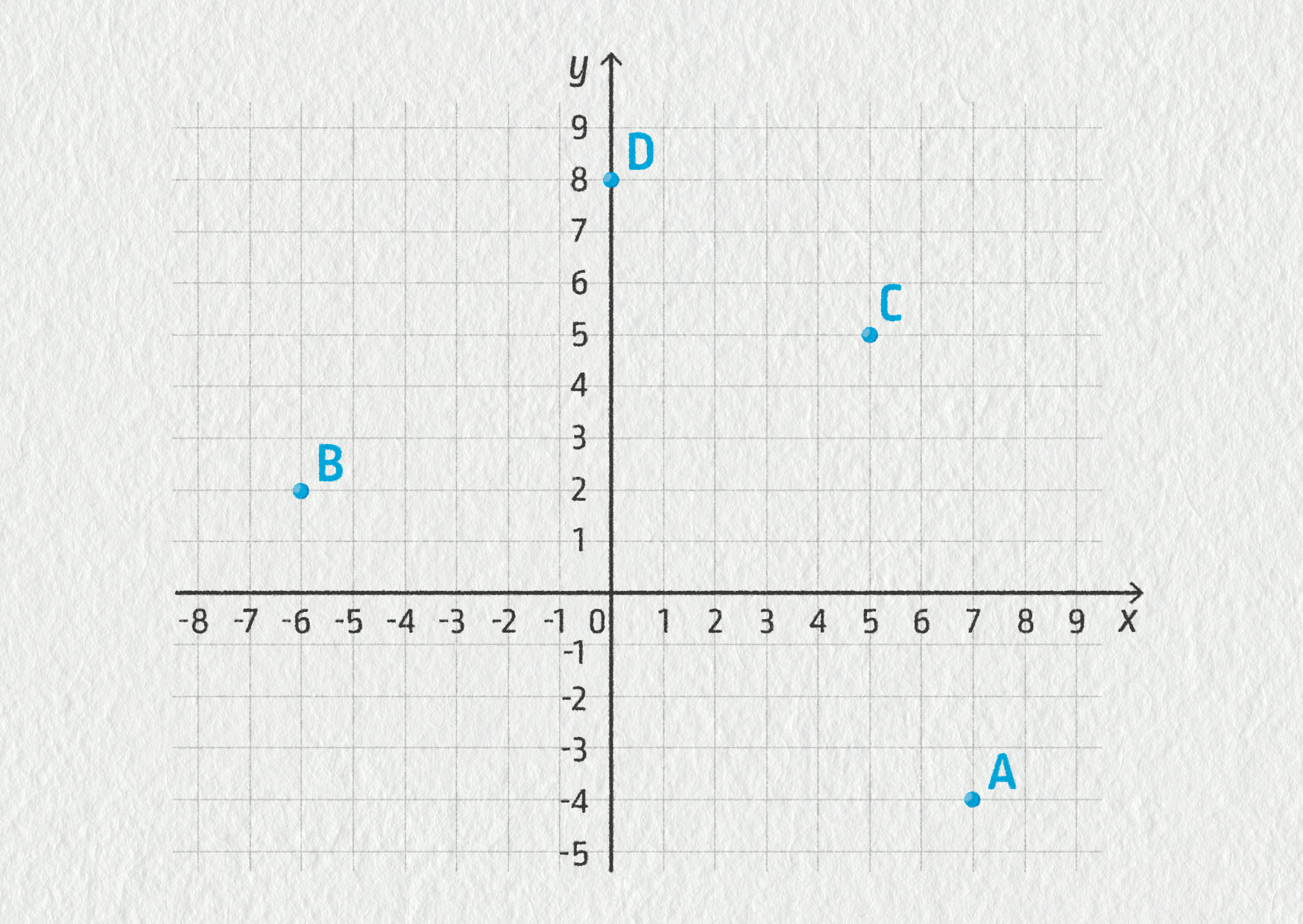
Zdroj
\(\Vec{r}_A=(7;-4)\), \(\Vec{r}_B=(-6;2)\), \(\Vec{r}_C=(5;5)\), \(\Vec{r}_D=(0;8)\)

Cvičení 2

Zakreslete do kartézského souřadnicového systému polohové vektory \(\Vec{r}_1=(-4;3)\), \(\Vec{r}_2=(7;1)\), \(\Vec{r}_3=(7;-4)\), \(\Vec{r}_4=(2;-8)\)

14.43 – Polohové vektory – řešení.
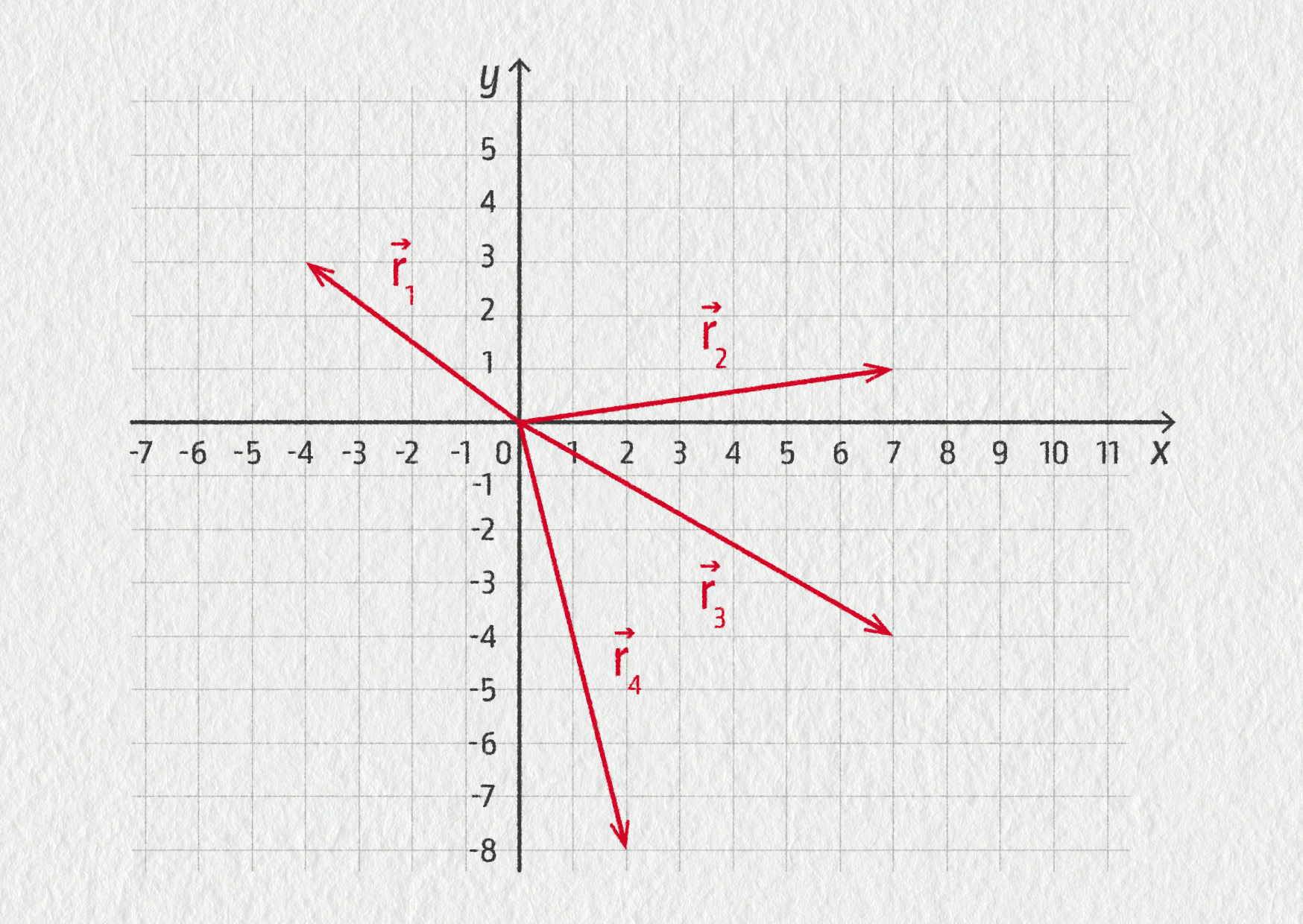
Zdroj

Cvičení 3

Mirek sedí v učebně fyziky (viz nákres).

14.44 – Jak sedí žáci ve třídě?
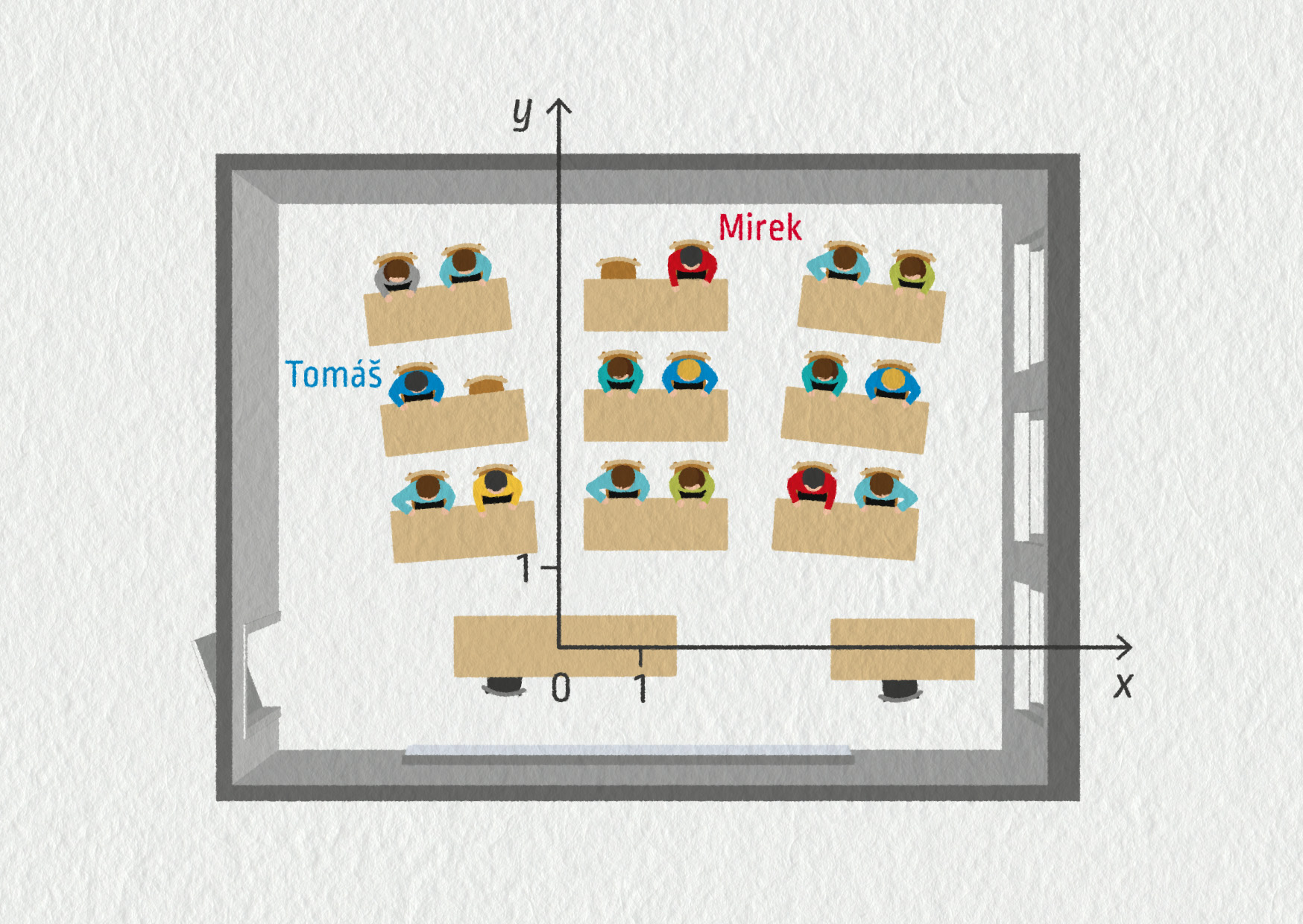
Zdroj
  1. Určete polohový vektor, který určuje jeho místo v dané souřadnicové soustavě.
  2. Zapište vektor posunutí, když přejde za Tomášem, aby si půjčil zapomenuté pravítko.
  3. Nakreslete oba vektory do obrázku.
  4. Jaké budou složky vektoru posunutí, když se bude vracet zpět na své místo?
  5. Mirkovi se líbí spolužačka Marcela. Obvykle sedává na místě o souřadnicích (3 m; 1,5 m). Vidí na ni Mirek ze svého místa?
  1. \(\Vec{r}_\mathrm{M}=(1\ \mathrm{m};4{,}5\ \mathrm{m})\)
  2. \(\Vec{r}_\mathrm{T}=(-2\ \mathrm{m};3\ \mathrm{m})\), \(\Delta\Vec{r}=\Vec{r}_\mathrm{T}-\Vec{r}_\mathrm{M}=(-3\ \mathrm{m};-1{,}5\ \mathrm{m})\)
  3. řešení je na obrázku
  4. \(\Delta\Vec{r}=\Vec{r}_\mathrm{M}-\Vec{r}_\mathrm{T}=(3\ \mathrm{m};1{,}5\ \mathrm{m})\)
  5. ano, vidí
14.45 – Jak sedí žáci ve třídě – řešení.
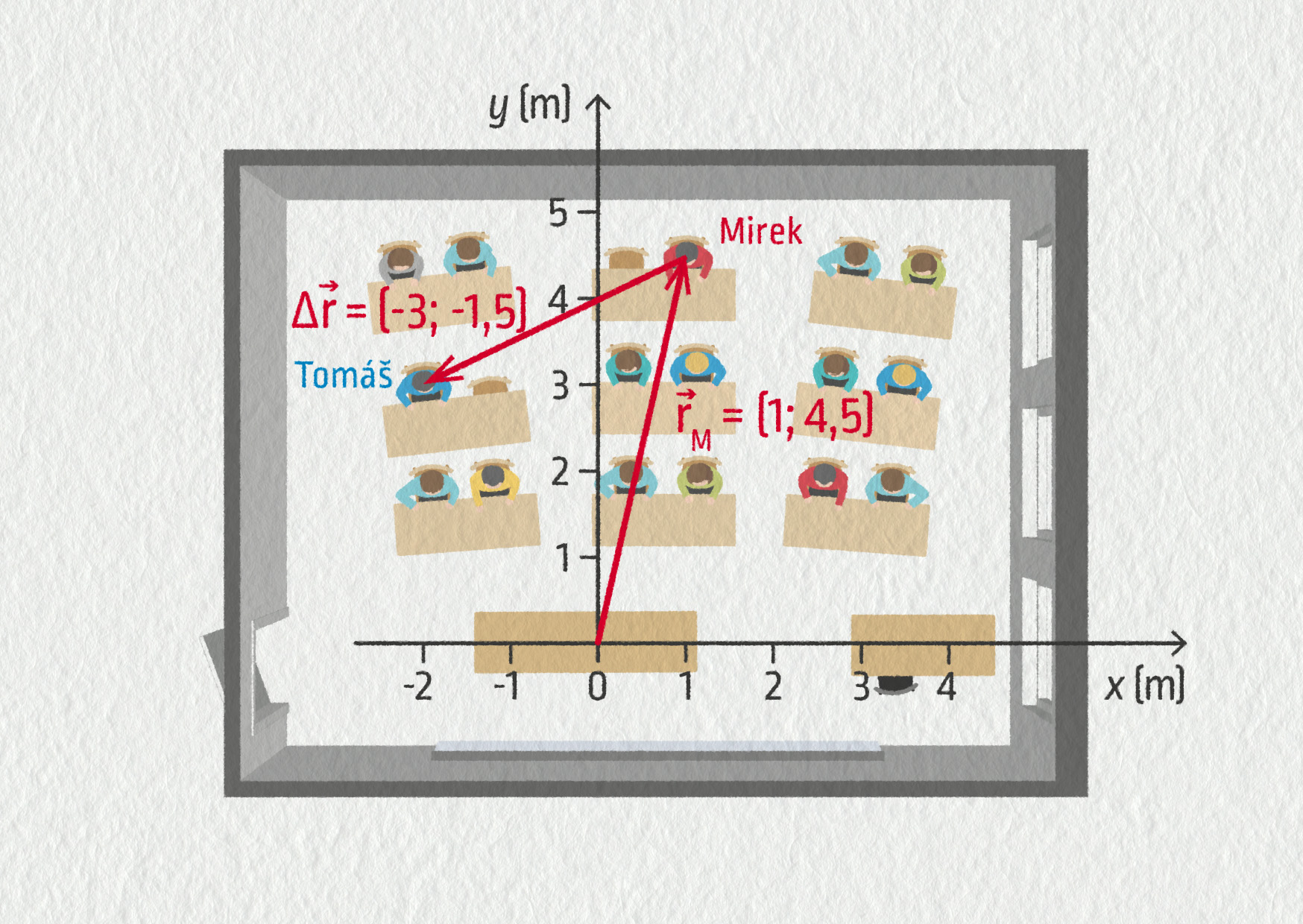
Zdroj

Cvičení 4

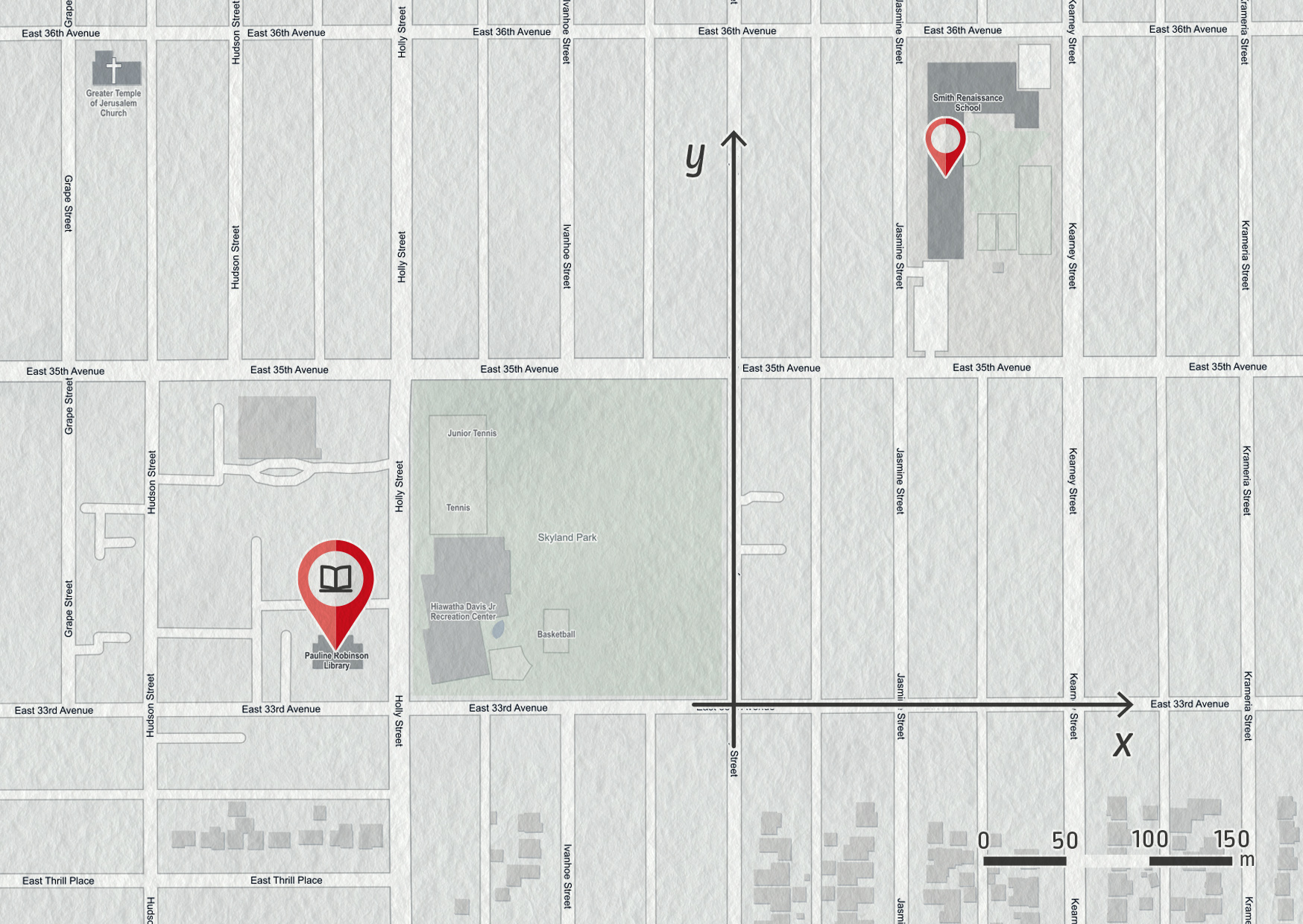
Andrew má v plánu navštívit po vyučování knihovnu Pauliny Robinsonové (Denver, USA).

14.46 – Cesta do knihovny.
Zdroj
  1. Určete souřadnice jeho školy Smith Renaissance School a souřadnice knihovny v zadaném souřadnicovém systému.
  2. Určete vektor posunutí mezi školou a knihovnou.
  3. Vypočítejte velikost vektoru posunutí. Odpovídá tato vzdálenost uražené vzdálenosti? Vysvětlete.
  1. \(\Vec{r}_\mathrm{s}=(150\ \mathrm{m};350\ \mathrm{m}\), \(\Vec{r}_\mathrm{l}=(-250\ \mathrm{m};50\ \mathrm{m})\)
  2. \(\Delta\Vec{r}=\Vec{r}_\mathrm{l}-\Vec{r}_\mathrm{s}=(-400\ \mathrm{m};-300\ \mathrm{m})\)
  3. \(|\Delta\Vec{r}|=500\ \mathrm{m}\), neodpovídá, uražená vzdálenost je větší

Cvičení 5

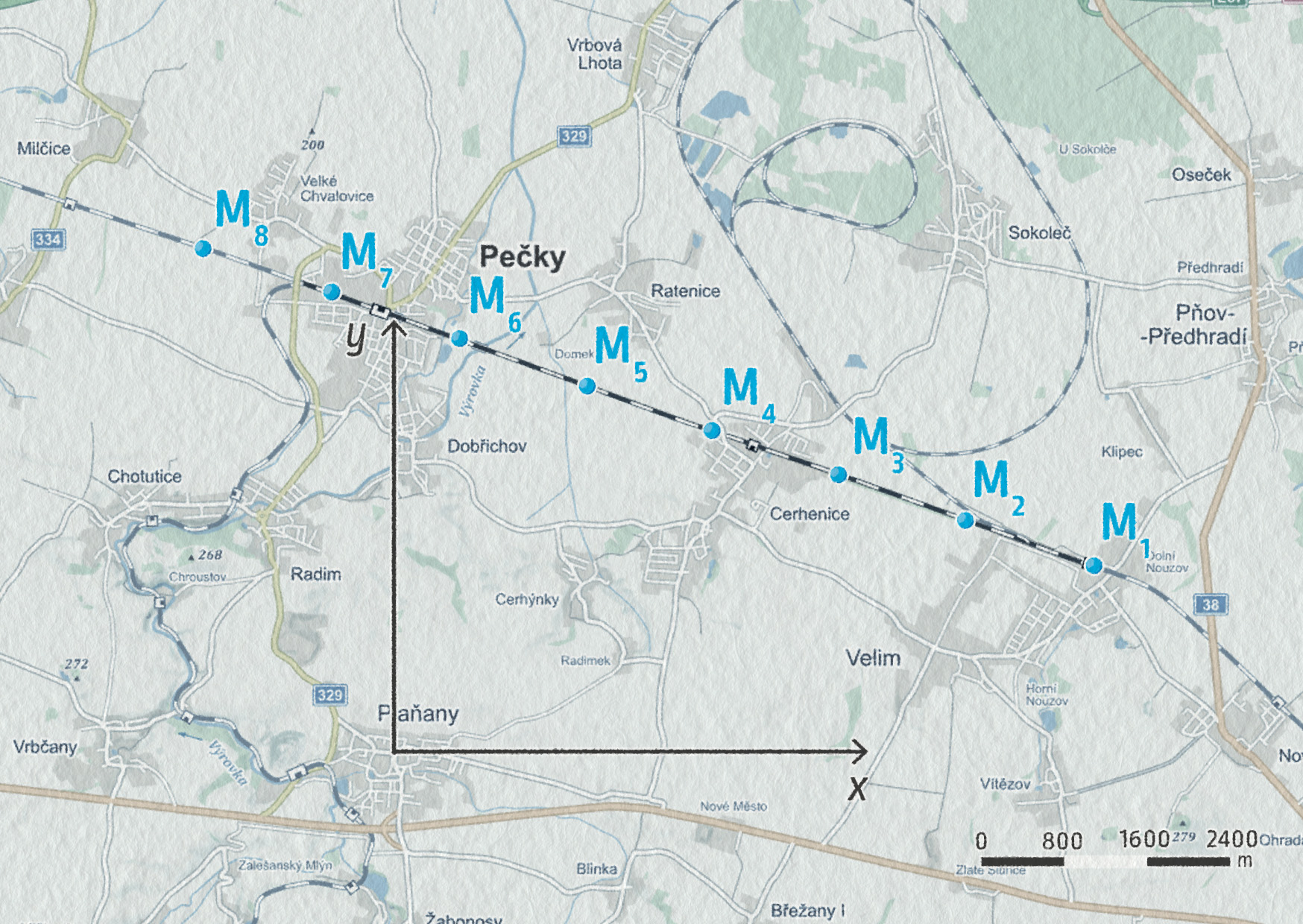
Vlaky mezi Kolínem a Prahou jezdí velmi rychle. Za Velimí následuje naprosto přímý úsek, kde vlaky dosahují maximálních rychlosti.

14.47 – Záznam pohybu vlaku mezi Velimí a Pečkami.
Zdroj
  1. Popište pohyb vlaku dle tvaru trajektorie.
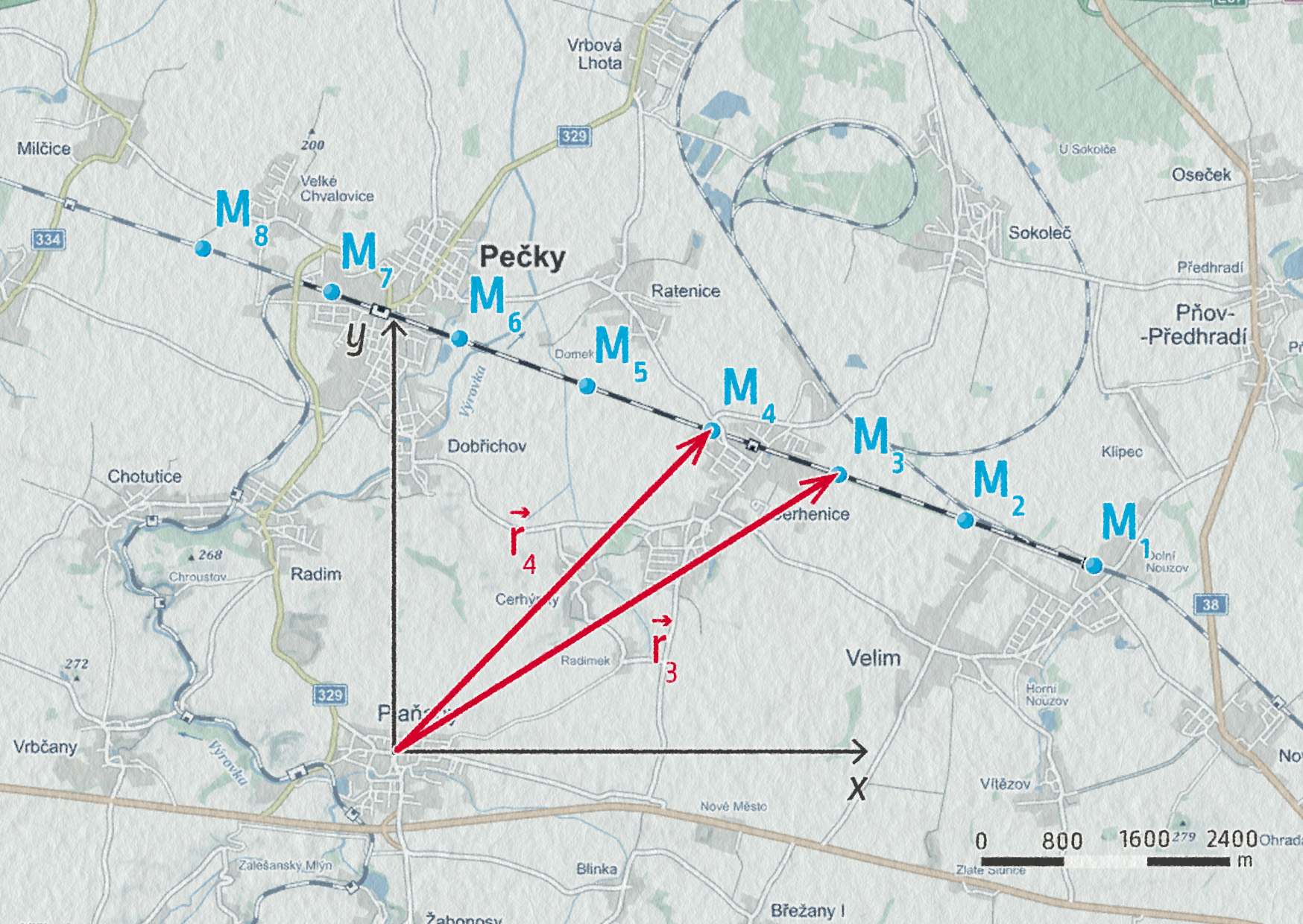
  2. Časový interval, který uplynul mezi označením dvou po sobě jdoucích poloh obrázku, je 30 s. Polohu vlaku budeme zaznamenávat vůči městu Plaňany. Znázorněte polohové vektory vlaku v bodech M3 a M4. Co o nich můžete říci?
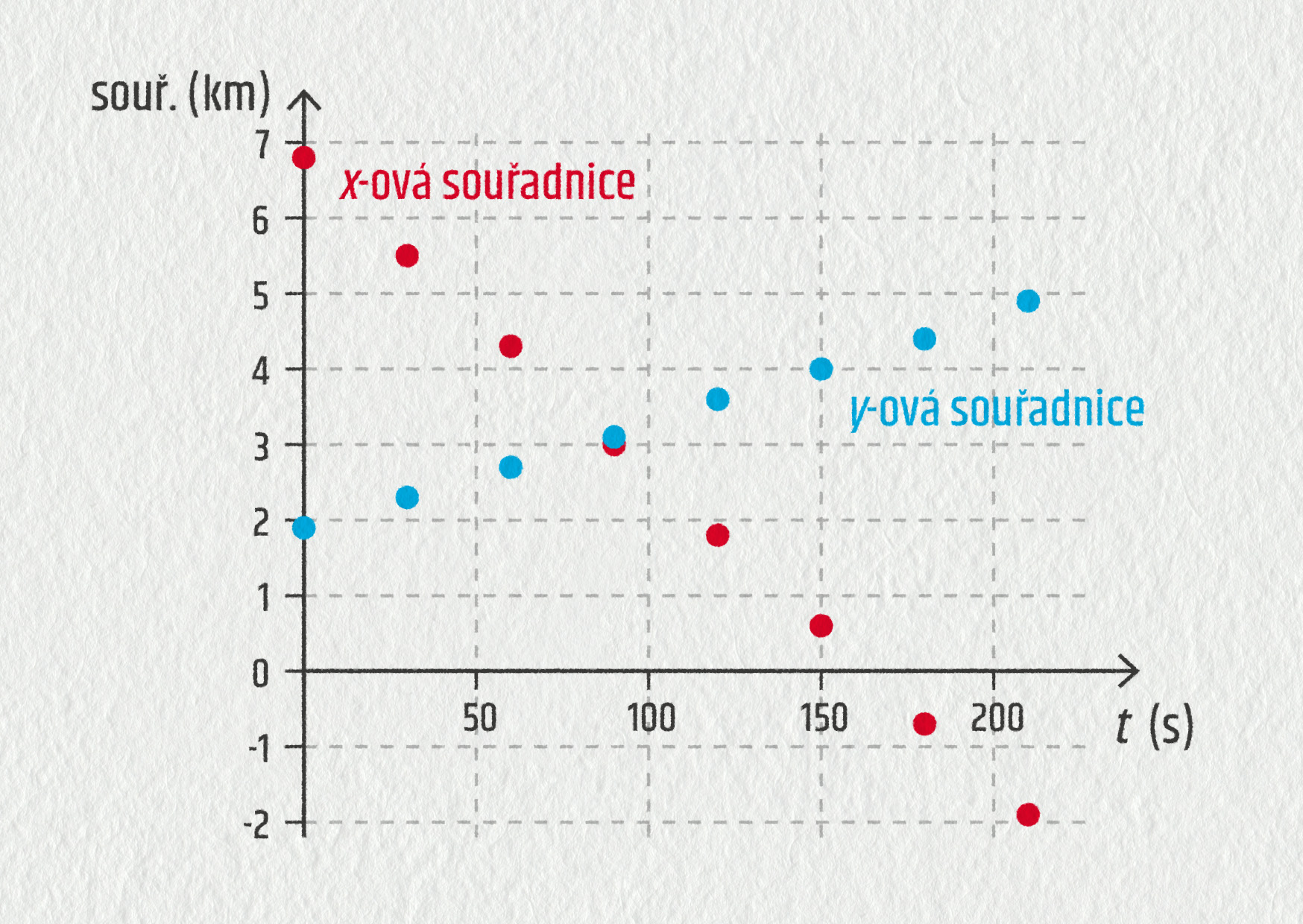
  3. Zaneste do tabulky složky všech vektorů polohy z tohoto příkladu:
    polohový vektor x-ová složka polohového vektoru (km) y-ová složka polohového vektoru (km)
    \(\Vec{r}_1\)
    \(\Vec{r}_2\)
    \(\Vec{r}_3\)
    \(\Vec{r}_4\)
    \(\Vec{r}_5\)
    \(\Vec{r}_6\)
    \(\Vec{r}_7\)
    \(\Vec{r}_8\)
  4. Sestrojte grafy x-ové a y-ové souřadnice v závislosti na čase.
  5. Jak budou tyto grafy vypadat, když bude vlak stát v zastávce?
  1. rovnoměrný přímočarý pohyb;
  2. vektory nejsou shodné, poloha se mění, \(\Vec{r}_3=(4{,}3\ \mathrm{km};2{,}7\ \mathrm{km})\), \(\Vec{r}_4=(3{,}0\ \mathrm{km};3{,}1\ \mathrm{km})\), \(\Vec{r}_3\ne\Vec{r}_4\), polohové vektory jsou na obrázku;
  3. složky polohových vektorů jsou v tabulce;
  4. souřadnice jsou zakresleny v obrázku;
  5. jestliže vlak stojí v zastávce, grafem složek polohového vektoru jsou konstantní funkce
14.48 – Záznam pohybu vlaku mezi Velimí a Pečkami – řešení.
Zdroj
polohový vektor x-ová složka polohového vektoru (km) y-ová složka polohového vektoru (km)
\(\Vec{r}_1\) 6,8 1,9
\(\Vec{r}_2\) 5,5 2,3
\(\Vec{r}_3\) 4,3 2,7
\(\Vec{r}_4\) 3,0 3,1
\(\Vec{r}_5\) 1,8 3,6
\(\Vec{r}_6\) 0,6 4,0
\(\Vec{r}_7\) −0,7 4,4
\(\Vec{r}_8\) −1,9 4,9
14.49 – Změny polohového vektoru.
Zdroj

Cvičení 6

Těleso vykonává rovnoměrný pohyb. Jeho souřadnice splňují rovnice:

\[ x=2+3t \quad\hbox{a}\quad y=-4+2t\;, \quad t\in\Bbb{R}\;. \]

Zakreslete polohy tělesa v rovině pro \(t=0,1,\dots,5\). Jaký je tvar trajektorie tělesa?
Poznámka: Proměnná \(t\) představuje čas v sekundách. Souřadnice x a y jsou v metrech. Lineární koeficienty 3 a 2 představují složky rychlosti v m/s.

trajektorií tělesa je přímka, řešení je zakresleno na obrázku

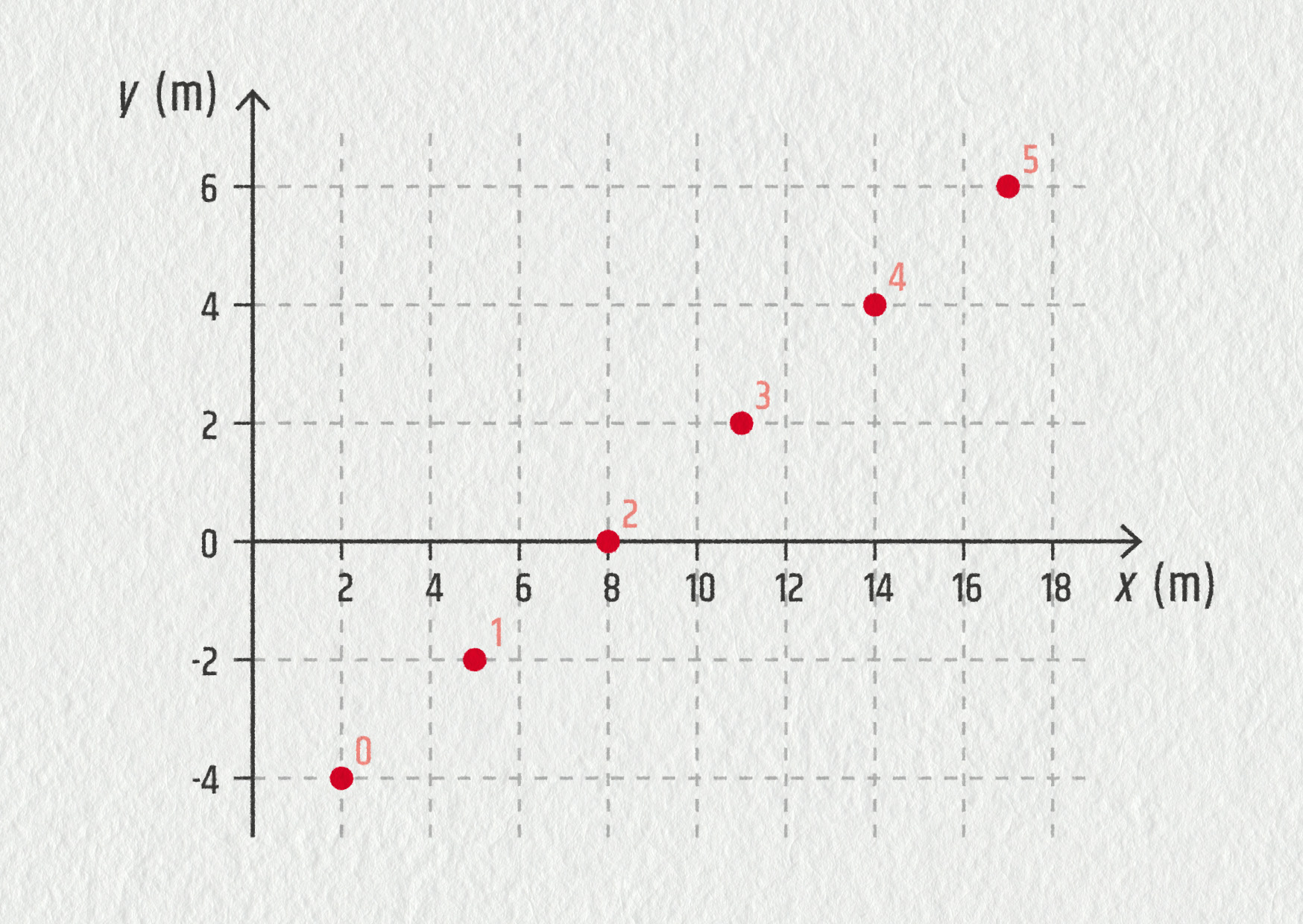
14.50 – Trajektorie tělesa – rovnoměrný přímočarý pohyb.
Zdroj

Cvičení 7

Těleso vykonává pohyb, jeho souřadnice splňují rovnice

\[ x=2t+3 \quad\hbox{a}\quad y=\frac{1}{4}t^2+4\;, \quad t\in\Bbb{R}\;. \]

Zakreslete polohy tělesa v rovině pro \(t=0,1,\dots,5\). Jaký je tvar trajektorie tělesa?

Poznámka: Proměnná \(t\) představuje čas v sekundách. Souřadnice x a y jsou v metrech. Lineární koeficient 2 odpovídá rychlosti ve směru osy \(x\) a kvadratický koeficient 1/4 souvisí se zrychlením ve směru osy \(y\).

trajektorie je křivka – parabola, řešení je zakresleno na obrázku

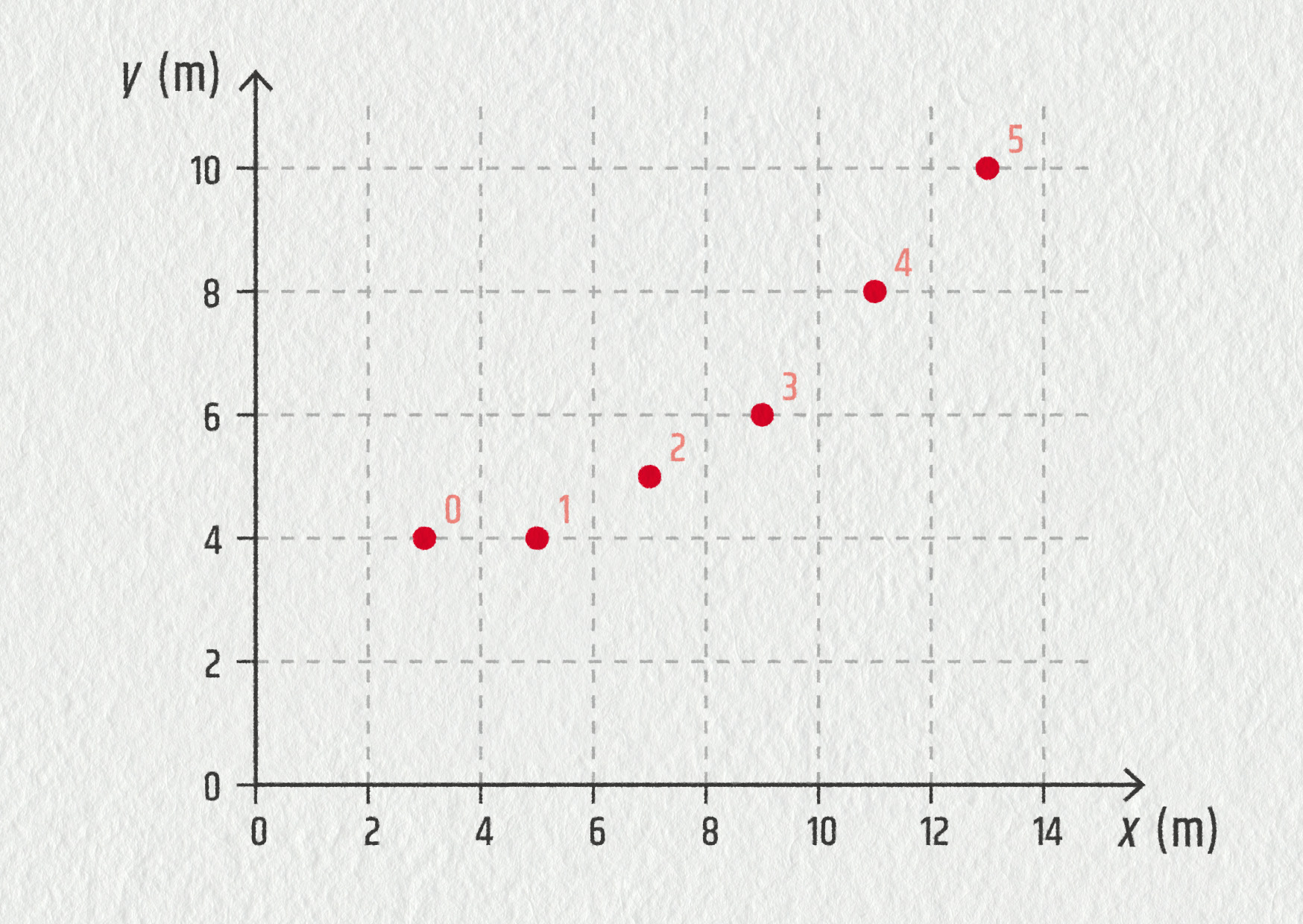
14.51 – Trajektorie tělesa – zrychlený křivočarý pohyb.
Zdroj
Tlačítko pro návrat zpět nahoru na stránce (back to top)