K popisu přírody používáme ve fyzice veličiny skalární a vektorové. Skalární veličiny jsou určeny jen svojí hodnotou (a jednotkou), patří mezi ně například délka, teplota, čas nebo hmotnost. Pomocí nich odpovídáme na otázku „kolik nebo jaký (kolik měří, jaká je hodnota naměřené teploty, kolik uběhlo času, kolik váží, jakou rychlostí… ?)“.
Například hmotnost (skalární veličinu) zjišťujeme nejčastěji vážením. Postavíme-li na váhu dvoukilogramové závaží, váha ukáže 2 kg. O hmotnosti získáme úplnou informaci, která je vyjádřena číslem a jednotkou: 2 kg.
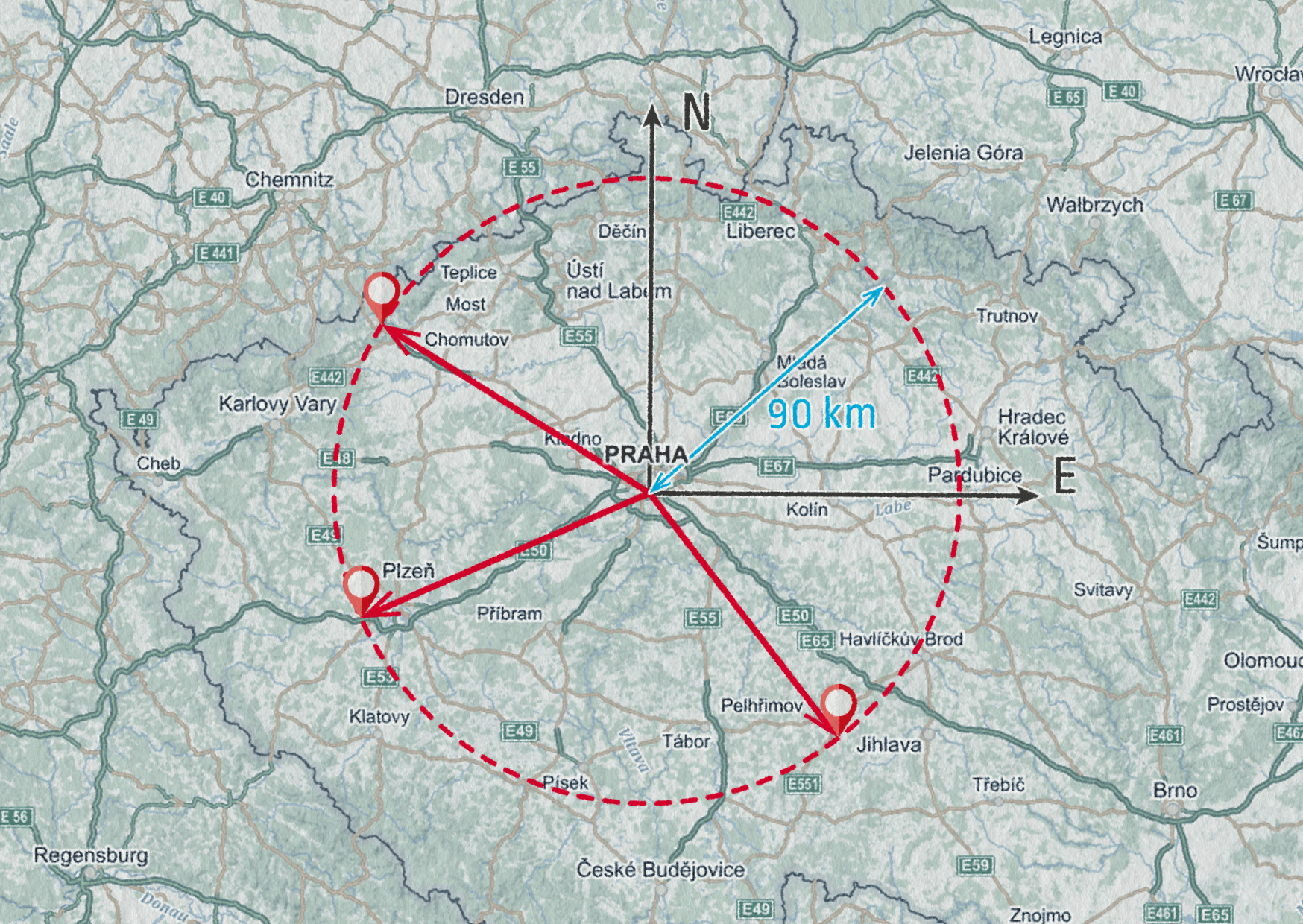
Poznali jsme také, že existují i veličiny jiného druhu – veličiny vektorové. Představme si, že máme vypustit meteorologický balón v Praze-Libuši. Kde pak takový balón dopadne? Kam se ho máme vydat hledat, když víme jenom, že to bude asi 90 km od Prahy? K Chomutovu? Za Plzeň nebo k Pelhřimovu?
Zdroj
Najednou nestačí zadat pouze vzdálenost. Musíme také určit směr, ve kterém se balón pohybuje. Například na jihovýchod. a hned je jasné, že sonda míří k Pelhřimovu.
Vektorové veličiny jsou určeny svojí hodnotou a směrem. Odpovídají současně na otázky „kolik“ a „jakým směrem?“. Nesmíme ani v tomto případě opomenout jednotku dané veličiny.
Do schémat se znázorňují šipkou, v textu se používá zápis se šipkou nad symbolem \(\vec{F}\), nebo tučná kurzíva \(\boldsymbol{F}\). Příkladem vektorové veličiny je kromě síly \(\Vec{F}\) také rychlost \(\Vec{v}\), zrychlení \(\Vec{a}\) nebo intenzita elektrického pole \(\Vec{E}\).

