Rychlost
Cvičení 1
Ve vchodu do metra jedou proti sobě dvoje pohyblivé schody. Cestující jedoucí vzhůru (pan A) má rychlost o velikosti 1,6 m/s.
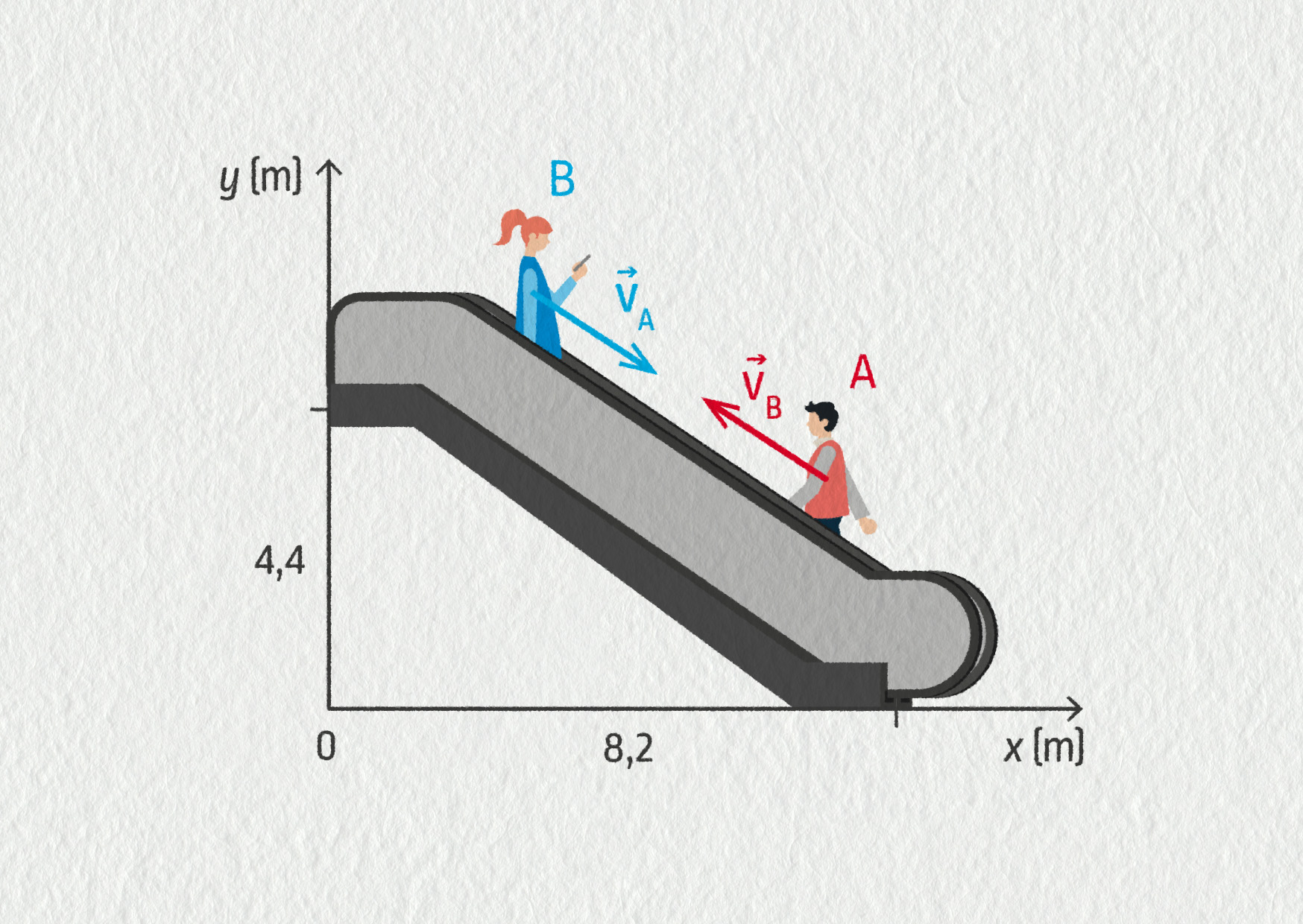
Zdroj
- Určete složky rychlosti pana A.
- Jaké jsou složky rychlosti druhého cestujícího (slečna B), jestliže je velikost rychlosti pohyblivých schodů stejná?
- Jaká je trajektorie obou pohybů?
- Určete velikost rychlosti a její složky pohybu prvního cestujícího vůči druhému.
- \(v_{xA}=-1{,}4\ \mathrm{m/s}\), \(v_{yA}=0{,}76\ \mathrm{m/s}\);
- \(v_{xB}=1{,}4\ \mathrm{m/s}\), \(v_{yB}=-0{,}76\ \mathrm{m/s}\);
- trajektorií je přímka,
- \(v_{xAB}=-2{,}8\ \mathrm{m/s}\), \(v_{yAB}=1{,}5\ \mathrm{m/s}\)
Cvičení 2
Vážka se na naší zemi vyskytuje již přes 250 milionů let a za tu dobu si stačila vyvinout zajímavou a velice účinnou strategii letu. Je velice rychlá a umí za letu manévrovat mnohem obratněji než jakýkoliv jiný hmyz. Aby se pro svou kořist jevila menší, skládá za letu nohy za svou hlavu. Dokonce uplatňuje zajímavou loveckou strategii, jejímž cílem je přiblížit se ke své kořisti nepozorovatelně.

Zdroj
Základní myšlenkou této lovecké strategie je pohybovat se takovým způsobem, že se kořisti bude zdát, že vážka je stále na stejném místě. Ačkoliv se ke své kořisti přibližuje, z jejího pohledu bude stále na stejném místě, a když zaregistruje, že se vážka příliš přiblížila, již bude pozdě, aby jí unikla.
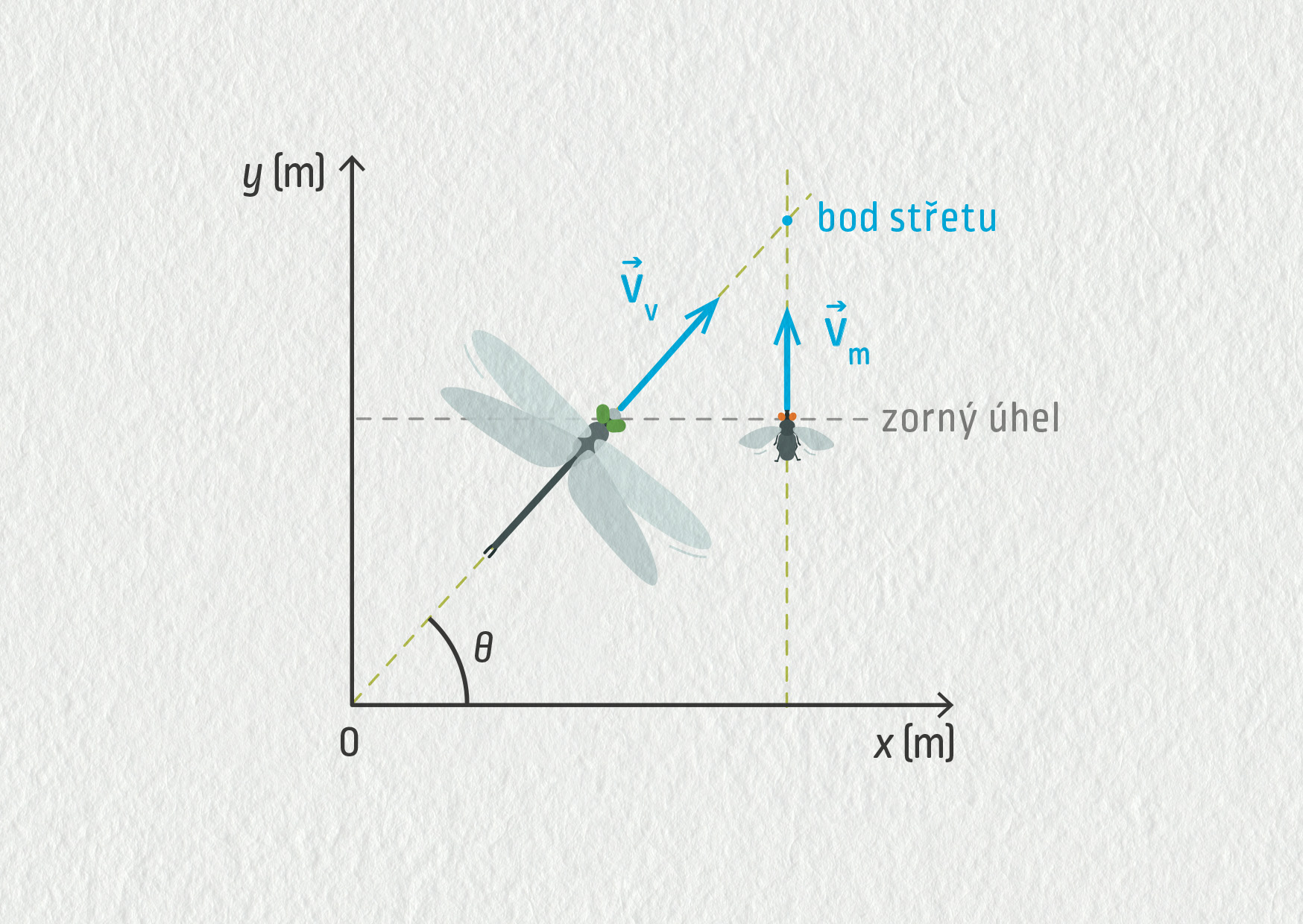
Zdroj
Představme si, že takový lov probíhá následujícím způsobem. Moucha se pohybuje ve směru osy y rychlostí o velikosti \(v_\mathrm{m}=0{,}750\ \mathrm{m/s}\) a vážka se přibližuje pod úhlem 48,5° vzhledem k ose \(x\) konstantní rychlostí \(v_\mathrm{v}\).
Jaká musí být rychlost vážky \(v_\mathrm{v}\), aby se pohybovala stále na stejné úrovni jako moucha, a stala se tak pro ni „neviditelná“?
- 0,562 m/s
- 0,664 m/s
- 1,00 m/s
- 1,13 m/s
Řekněme, že nyní letí vážka ve směru, který svírá s osou \(x\) úhel \(\theta>48{,}5^\circ\). Je v tomto případě rychlost vážky \(v_\mathrm{v}\) větší, stejná nebo menší než v předchozím případě?
- větší
- stejná
- menší
Jakou rychlostí se musí vážka přibližovat ke kořisti, jestliže „nalétává“ pod úhlem \(\theta=68{,}5^\circ\)?
- 0,295 m/s
- 0,698 m/s
- 0,806 m/s
- 2,05 m/s
Pod jakým úhlem se vážka přibližuje ke kořisti, jestliže letí rychlostí o velikosti \(v_\mathrm{v}=0{,}950\ \mathrm{m/s}\)?
- 37,9°
- 39,3°
- 51,7°
- 52,1°
- 1,00 m/s;
- menší;
- 0,806 m/s;
- 52,1°
Cvičení 3
Určete velikost rychlosti tělesa v bodech M4 a M9 na záznamu dle následujícího obrázku.
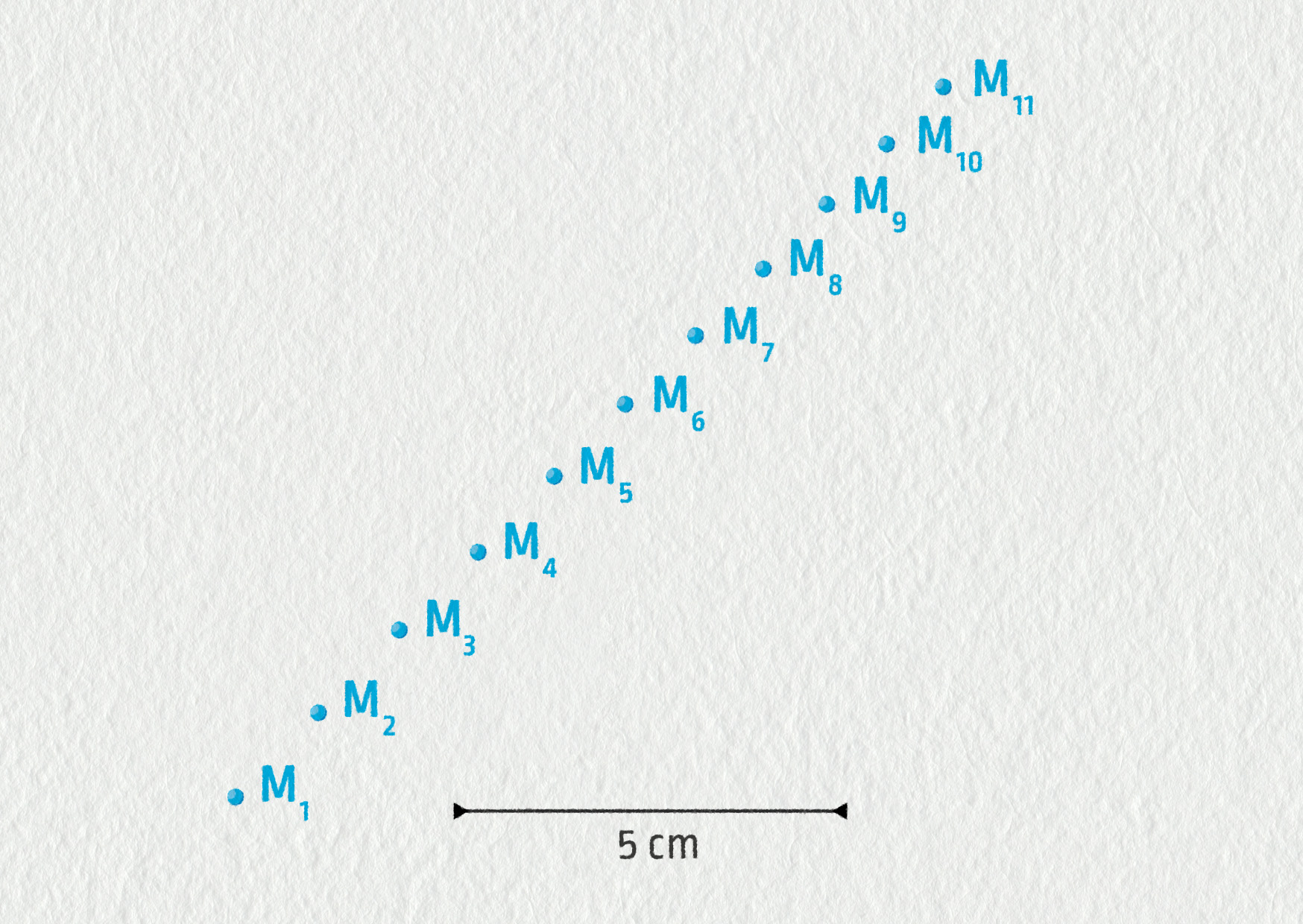
Zdroj
Rychlosti \(\Vec{v}_4\) a \(\Vec{v}_9\) zakreslete do obrázku. Doba, která uplynula mezi dvěma po sobě jdoucími pozicemi, je \(\tau=50\ \mathrm{ms}\). Doporučené měřítko: 1 cm odpovídá 6 cm/s. (PDF ke stažení)
Jaké jsou složky rychlosti v těchto bodech? Tyto složky správně zapište.
\(v_4=30\ \mathrm{cm/s}\), \(v_9=24\ \mathrm{cm/s}\); složky rychlosti závisí na volbě soustavy souřadnic (orientaci os), více možných řešení
Cvičení 4
Na počátku září 2008 přerostla tropická bouře v Antlantiku na hurikán jménem Ike.
Během prvních tří dnů byly jeho souřadnice následující:
| latitude (°N) | longitude (°W) | |
|---|---|---|
| 1. září 2008 | 17,2 | 37 |
| 3. září 2008 | 19,8 | 47,3 |
| 5. září 2008 | 23,6 | 59 |
| 6. září 2008 (předpověď) | ||
| 6. září (skutečnost) |
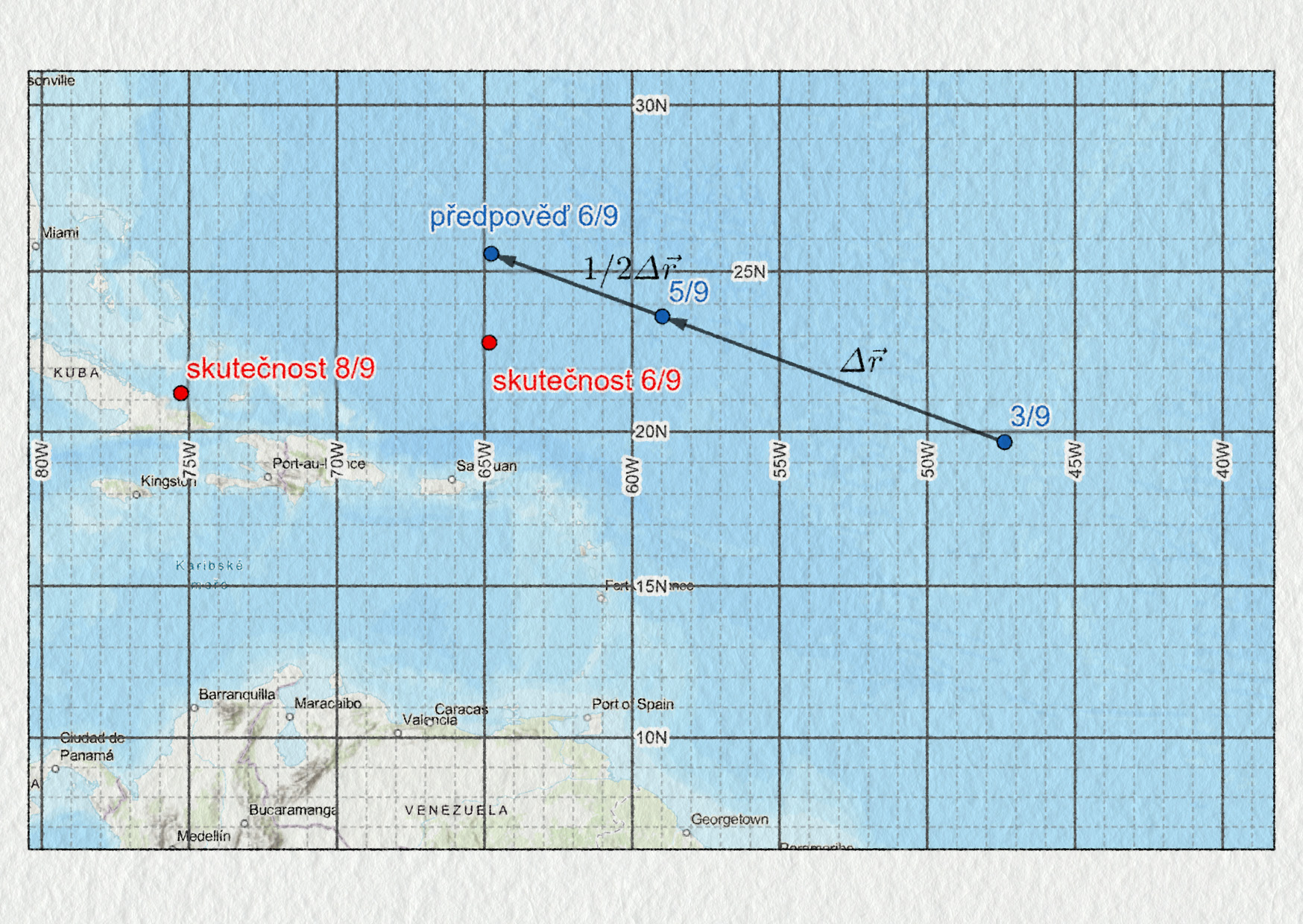
- Zakreslete polohu hurikánu do mapy (viz soubor ke stažení).
- Vytvořte předpověď dalšího pohybu hurikánu na základě analýzy dat z předchozích dnů.
- Určete skutečnou polohu hurikánu dne 6. září 2008, jestliže víte, že za 24 hodin se posunul o −0,8°N a 5,9°W. Odpovídá to vaší předpovědi?
- Jestliže za další dva dny se hurikán posunul o −1,7°N a 10,3°W, můžeme říci, že míří na Floridu, na Kubu nebo na Dominikánskou republiku?
- Pokud vás zajímá, jak se situace vyvíjela dál, podívejte se na stránku National Hurricane Center.
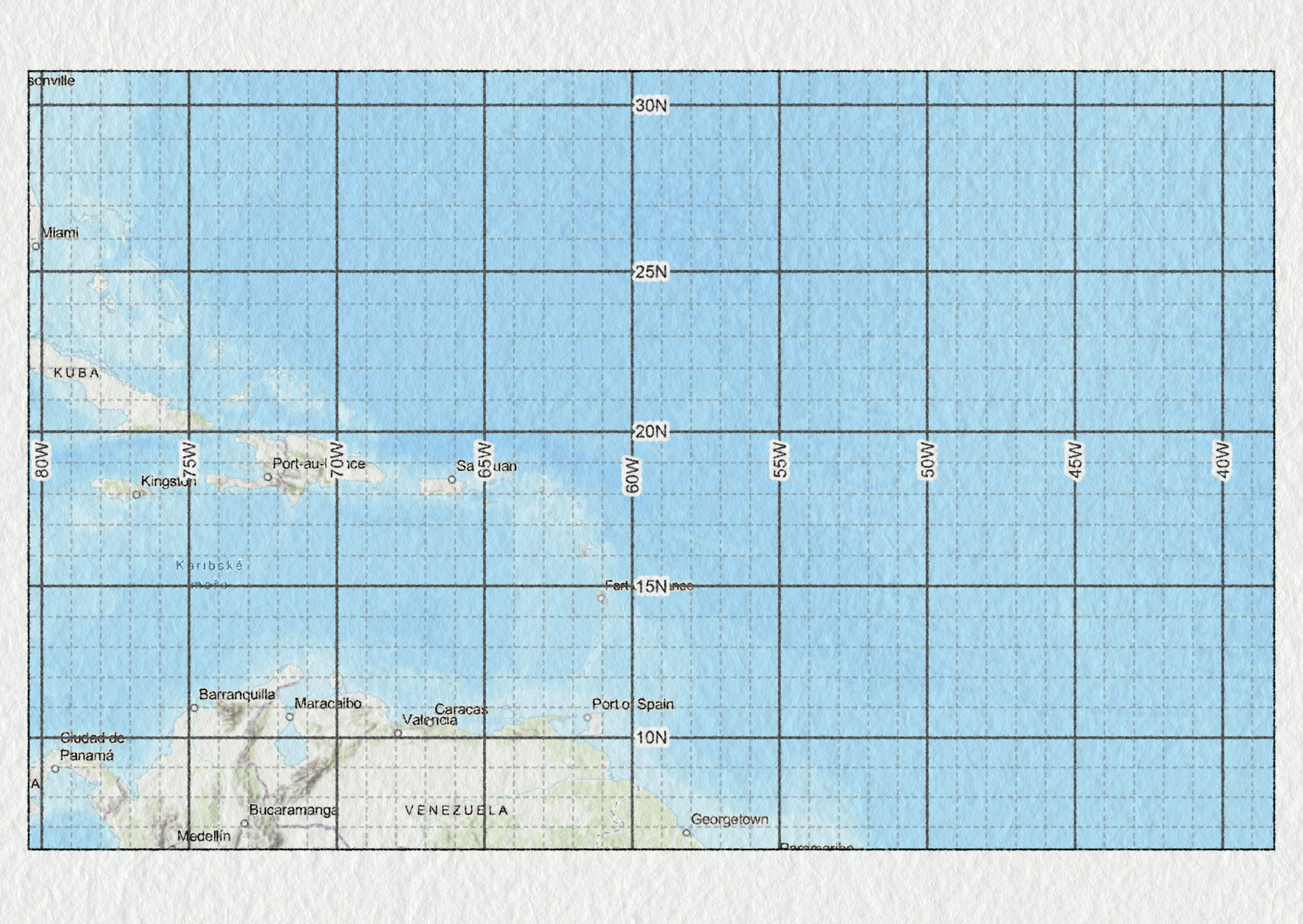
Zdroj
Zdroj
Cvičení 5
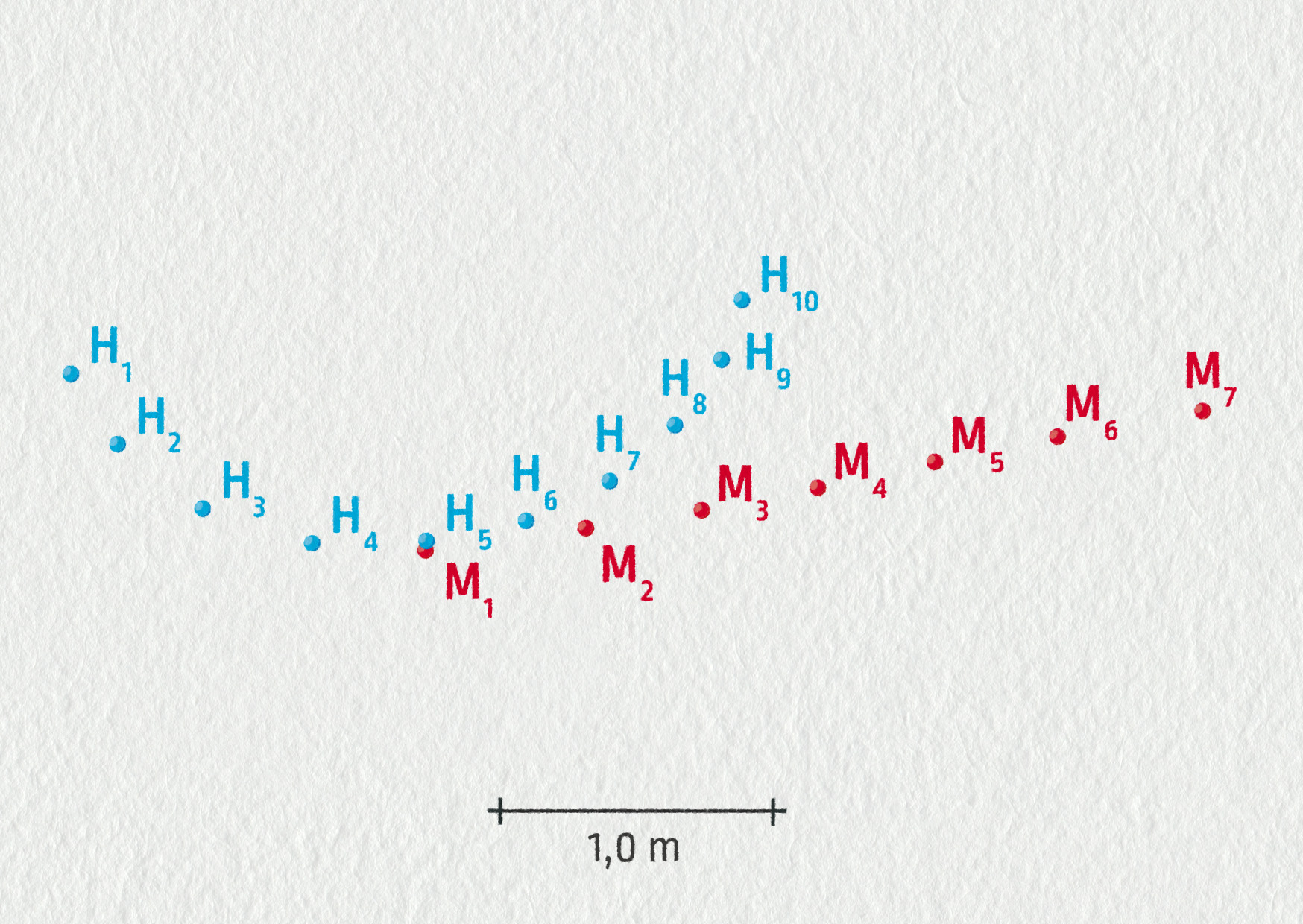
Následující fotografie golfového hráče byla vytvořena pomocí zábleskového zařízení, které osvětlovalo pohybujícího se hráče v intervalech 1/50 s. Výška postavy hráče je 1,80 m. Předpokládejme, že pohyb nastal v rovině kolmé k povrchu Země.
- Sestrojte vektory rychlosti konce golfové hole těsně před tím a těsně potom, než uvede míček do pohybu. Upřesněte použité měřítko.
- Jaká je rychlost golfového míčku po uvedení do pohybu?
- Vypočítejte velikost zrychlení míčku po jeho uvedení do pohybu.

Zdroj
Zdroj
Více o golfu: https://www.jamkoviste.cz/zajimavosti/285-rychlost-golfoveho-micku/
- \(v_{\mathrm{H}4}=20{,}5\ \mathrm{m/s}\), \(v_{\mathrm{H}6}=18\ \mathrm{m/s}\)
- \(v_{\mathrm{M}2}=25{,}5\ \mathrm{m/s}\)
- \(a=1\,275\ \mathrm{m/s}^2\)

