Konstrukce vektoru rychlosti
Úkol: Zkonstruujte vektor rychlosti ze záznamu jednotlivých po sobě jdoucích pozic.
Teoretický úvod – jak můžeme získat záznam pohybu?

Zdroj
Pomocí kamery nebo mobilního telefonu můžeme snadno získat záznam pohybu. Videosekvence není nic jiného než řada rychle po sobě jdoucích obrázků zaznamenávajících určitou situaci. Obrázky jsou většinou snímány v pravidelných intervalech s frekvencí, která se může měnit od 24 FPS pro klasický film až po hodnoty, které přesahují 1000 FPS pro vysokorychlostní kamery. (FPS = frame per seconde znamená počet obrázků za sekundu). Časový interval, který odděluje dva po sobě jdoucí snímky, značíme \(\tau\). Odpovídá převrácené frekvenci nahrávání.
Kamera je nehybná vzhledem k pozadí snímku, a proto můžeme zaznamenat na každém snímku polohu studovaného předmětu. Snadno tak zaznamenáme na jeden snímek postupné polohy předmětu v pohybu. Abychom mohli provést kinematickou analýzu pohybu, musíme znát interval \(\tau\) a měřítko skutečných vzdáleností zobrazených na nahrávce. Předpokládáme, že fotografie znázorňuje kolmý náhled na situaci.
Záznam č. 1
Zobrazení ve skutečné velikosti, \(\tau=20\ \mathrm{ms}\).
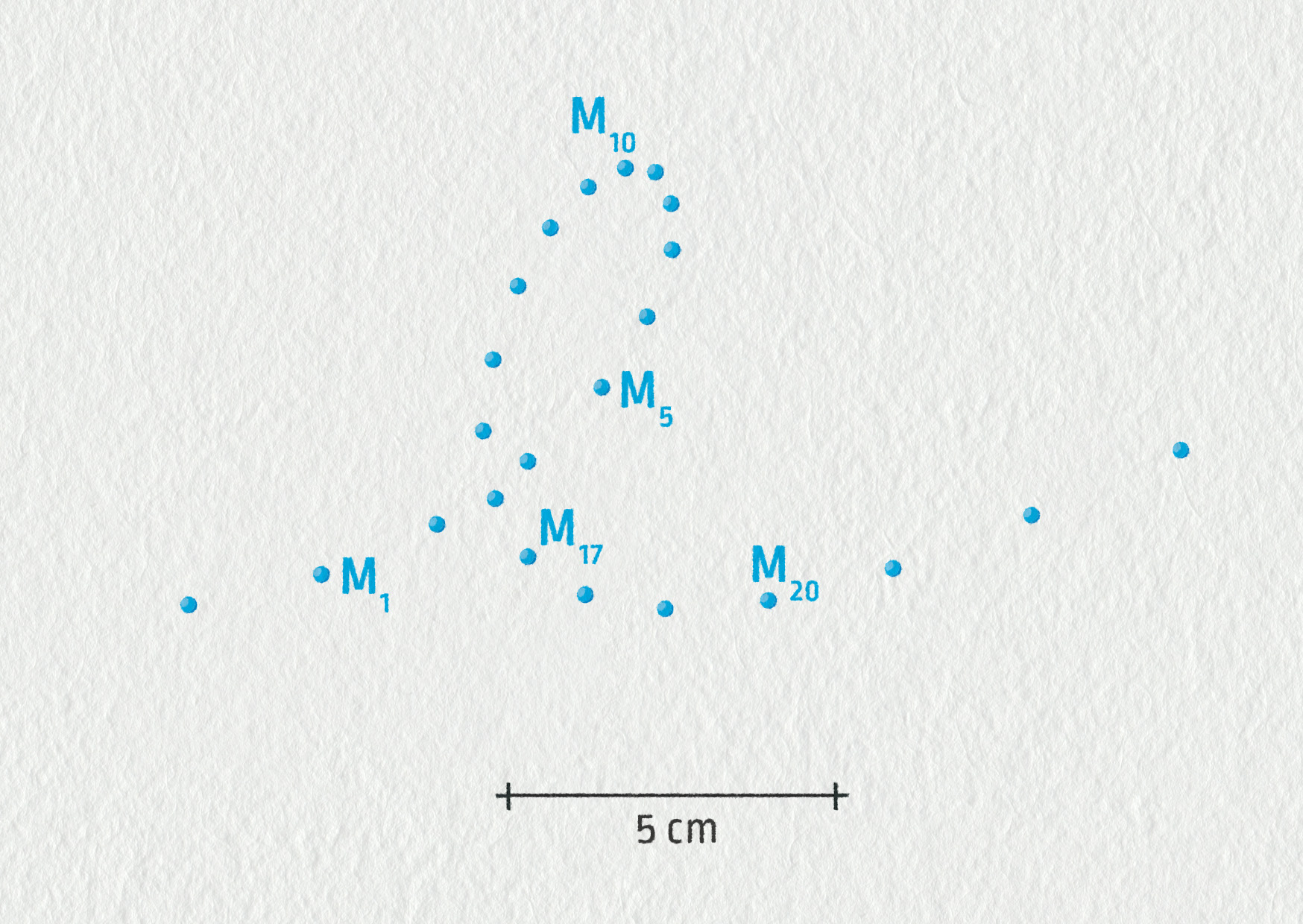
Zdroj
Nejprve vypočítejte velikost rychlosti v bodech M1, M5, M10, M17 a M20 a poté tyto vektory znázorněte do obrázku (ke stažení zde). Pro znázornění vektorů rychlosti použijte měřítko \(1\ \mathrm{m}/s \hat{=} 5\ \mathrm{cm}\).
Záznam č. 2
Zobrazení ve skutečné velikosti, \(\tau=40\ \mathrm{ms}\).
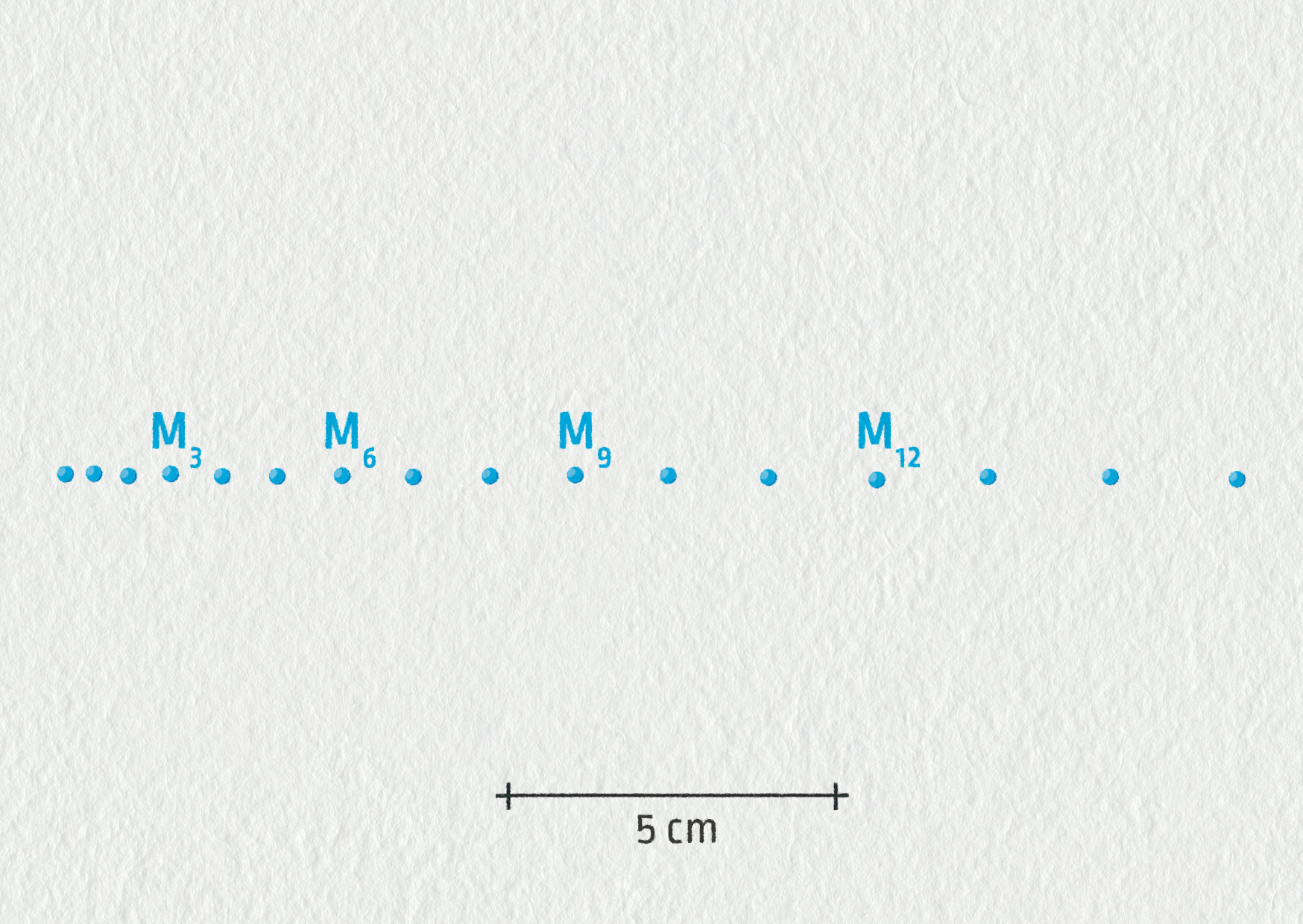
Zdroj
Nejprve vypočítejte hodnotu velikosti rychlosti v bodech M3, M6, M9 a M12 a poté tyto vektory znázorněte do obrázku (ke stažení zde). Pro znázornění vektorů rychlosti použijte vhodné měřítko, které také zapište do obrázku.
Za předpokladu, že jde o pohyb rovnoměrně zrychlený, určete hodnotu zrychlení \(a\) a velikost počáteční rychlosti \(v_0\) studovaného pohybu.
Záznam č. 3
Záznam pohybu je v měřítku 1 : 5 (1 cm na obrázku \( \hat{=} \) 5 cm ve skutečnosti), \(\tau=10\ \mathrm{ms}\).
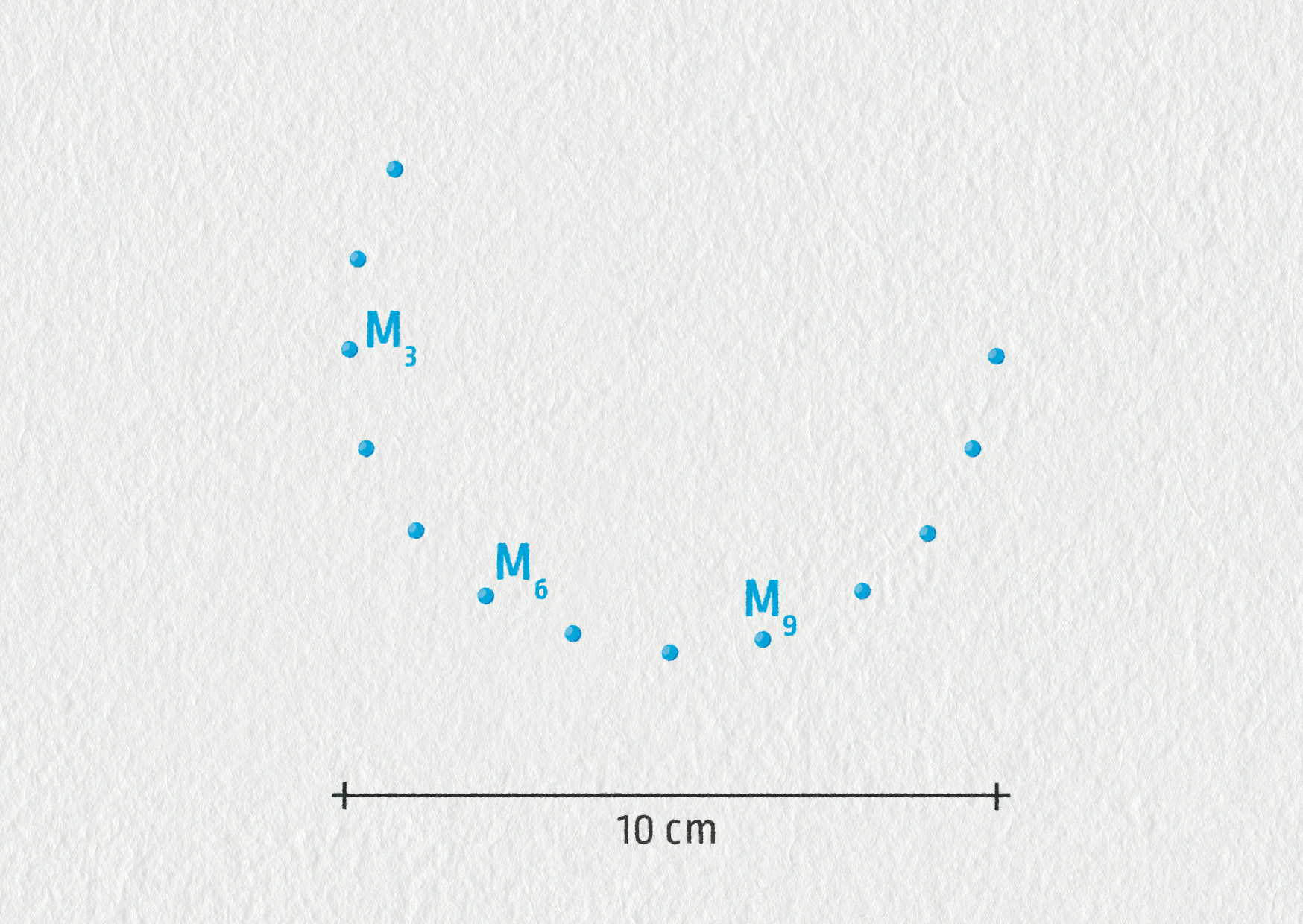
Zdroj
- Nejprve vypočítejte hodnotu velikosti rychlosti v bodech M3, M6, M9 a poté tyto vektory znázorněte do obrázku (ke stažení zde). Nezapomeňte uvést měřítko znázornění vektorů rychlosti.
- Najděte střed O kruhové trajektorie pohybu tělesa.
- Určete poloměr \(R\) této trajektorie.
- Jedná se o rovnoměrný pohyb?
- Jsou vektory rychlosti konstantní?

