Modelování trajektorií
Úkol: Vytvořte modely trajektorií pomocí programu Geogebra. Také prozkoumejte některé zajímavé křivky.
Vybavení: počítač
Trajektorie pohybu molekuly vzduchu v místnosti nebo člověka pohybujícího se po obchodním centru jsou složité a těžko matematicky popsatelné. Občas se však také setkáváme s pohyby, jejichž trajektoriemi jsou poměrně jednoduché křivky. Planeta obíhá kolem Slunce po elipse, vržený kámen letí přibližně po parabole, elektricky nabité částice se mohou v magnetickém poli pohybovat po šroubovicích. My zde nebudeme určovat tvary trajektorií v jednotlivých případech, ale naučíme se zobrazovat již známé trajektorie v programu Geogebra.
Použijeme k tomu dvě metody:
- souřadnice bodu jako funkce času,
- trajektorie jako křivka.
Obě jsou založené na tom, že souřadnice bodu budou záviset na parametru \(t\), který reprezentuje čas.
Postup:
- Seznamte se s návody konstrukce trajektorií v Geogebře (viz níže) a vyzkoušejte si, že dokážete znázornit jednoduchou trajektorii oběma způsoby.
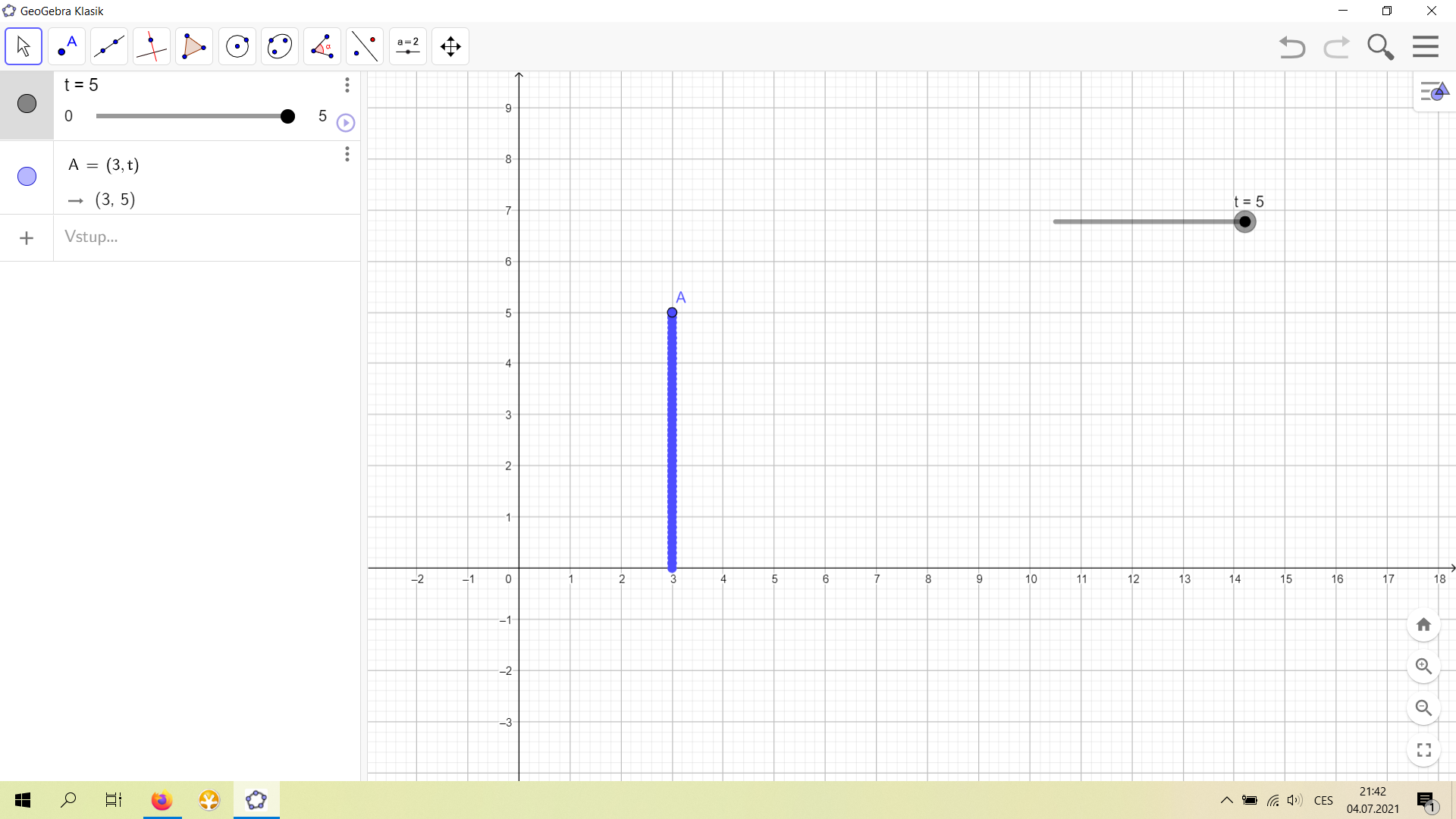
- Ve vzorovém příkladu jsme zvolili trajektorii bodu \((x,y)=(3,t)\). Jelikož v Geogebře nejsou jednotky, budeme pracovat v metrech a sekundách. To znamená, že pro náš bod platí: \(x=3\ \mathrm{m}\), \(y=1\ \mathrm{m/s}\cdot t\), kdy čas \(t\) je v rozmezí 0 s až 5 s. To představuje pohyb bodu po úsečce ve směru osy \(y\) rychlostí \(v=1\ \mathrm{m/s}\). Vyzkoušejte si nyní měnit rychlost a směr pohybu bodu a také jeho počáteční polohu. Nezapomeňte, že rychlost má v obecném případě dvě složky.
- Vyřešte pomocí grafů pohybu klasickou úlohu o pohybu: Vítek vyráží na koloběžce po rovné cestě od chalupy k rybníku rychlostí 2 m/s. Ve stejnou dobu mu vyráží naproti Tereza na kole rychlostí 5 m/s. Vzdálenost chalupy a rybníka je 2 400 m. Kde se obě děti potkají?
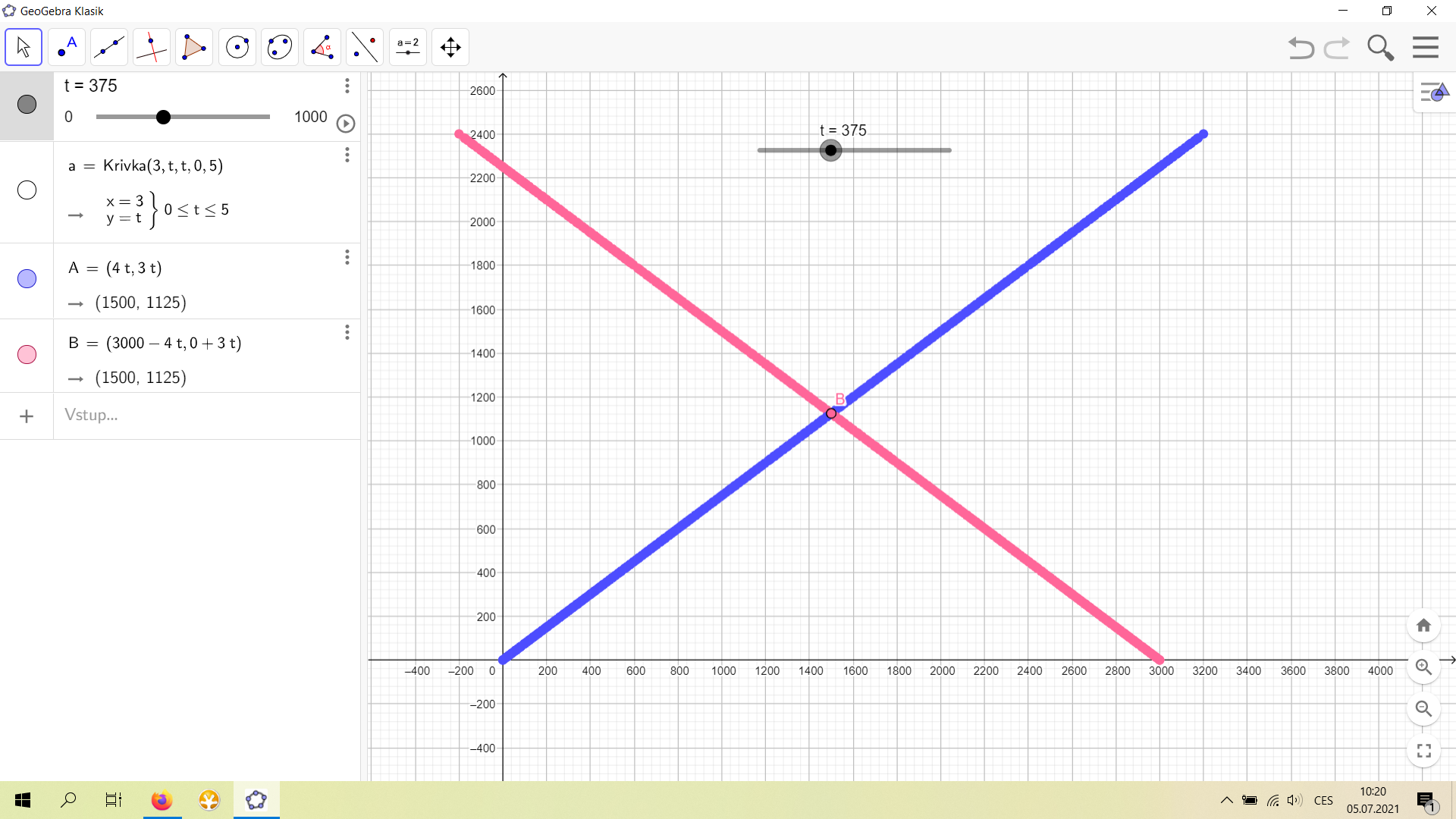
- Vyřešte pomocí modelování trajektorií 2D úlohu o pohybu: Vítek vyplul z přístavu v poloze \((0\ \mathrm{m};0\ \mathrm{m})\) rychlostí \(v=(4\ \mathrm{m/s};3\ \mathrm{m/s})\) a pokračuje stále dál na volné moře. Z pláže v poloze \((3\,000\ \mathrm{m};0\ \mathrm{m})\) za ním vyráží ve stejném okamžiku Tereza. Maximální velikost rychlosti člunu je 5 m/s. Jakou rychlostí musí Tereza plout, aby se s Vítkem setkala? Kdy a kde pak dojde k setkání? Uspořádejte malou soutěž, kdo se k Vítkovi dostane nejdřív!
- Nyní se můžeme pustit do modelování křivočarých trajektorií. Jelikož křivek je obrovské množství, vybrali jsme kružnici a jí příbuzné křivky. Prozkoumejte vliv různých parametrů na tvar křivek.
Otázky:
- Jak změníte rychlost a směr pohybu po kružnici?
- Jak změníte polohu kružnice v soustavě souřadnic?
- Jak nakreslíte jen vybranou část kružnice?
Návody konstrukce trajektorií v Geogebře
Souřadnice bodu jako funkce času:
- Vytvořte posuvník s proměnnou t, která bude reprezentovat čas, zvolte rozsah od 0 do 5.
- Vytvořte kdekoliv nový bod.
- Do okének pro souřadnice bodu zapište
(3, t). Poté pohybujte posuvníkem a sledujte pohyb bodu. Pokud chcete zobrazit trajektorii bodu, zvolte v jeho nastavení možnost „zobrazit stopu“. Váš bod by se měl pohybovat ve směru osy y, zatímco x-ová souřadnice bude stále rovna 3 (viz obrázek). - To je celé. Teď stačí zapisovat do závorek k souřadnicím bodu správné výrazy a můžete začít s modelováním (viz úkoly). Pokud byste chtěli, aby se bod pohyboval sám a plynule, můžete na posuvníku zvolit možnost „animace“.
Zdroj
Trajektorie jako křivka:
-
Přidejte nový objekt – křivku – pomocí následujícího schématu:
Krivka(Výraz, Výraz, Parametr proměnné, Poč. hodnota, Koncová hodnota)- Na místo prvního výrazu zapište
3(souřadnice x), - na místo druhého výrazu napište
t(souřadnice y), - na místo parametru proměnné napište
t(volba názvu parametru), - jako počáteční hodnotu napište
0(parametr t začne od nuly), - jako koncovou hodnotu napište
5(parametr t skončí hodnotou 5).
-
Měla by se vám vykreslit křivka, které se shoduje s trajektorií vytvořenou pohybem posuvníku.
-
To je celé. Teď stačí zapisovat do závorky ke křivce správné výrazy a můžete začít s modelováním (viz úkoly níže). V tomto případě nám Geogebra vykreslí celou trajektorii naráz jako křivku, nemůžeme tedy simulovat, jak se bod pohybuje. Zato však křivku máme narýsovanou přesněji než pomocí stopy.
Vybrané křivky
| kružnice | \((x,y)=(R\cos t,R\sin t)\) |
| elipsa | \((x,y)=(A\cos t,B\sin t)\) |
| spirála (Archimédova) | \((x,y)=(At\cos t,At\sin t)\) |
| cykloida | \((x,y)=(A(t-\cos t),A(1-\sin t))\) |
Poznámka: Do funkcí sinus a cosinus dosazujeme pouze číselnou hodnotu času.
Řešení úlohy v bodu 2:
K setkání dojde za 343 s ve vzdálenosti 686 m od chalupy.
Řešení úlohy v bodu 3: Toto je řešení, kdy se lodě setkají v nejkratším možném čase 375 s. Tereza musí mít rychlost (–4 m/s, 3 m/s).
Zdroj

