Jak zvážit Jupiter

Úkol: Určete hmotnost Jupiteru.

Vybavení: Program JupLab ke stažení na http://www3.gettysburg.edu/~marschal/clea/juplab.html

Princip:

V tomto praktiku si vyzkoušíte základní metodu, kterou astronomové používají k určování hmotnosti vesmírných objektů. Je založena na obíhání pozorovatelných těles kolem daného objektu a využití 3. Keplerova zákona. Tímto způsobem je možné „zvážit“ Zemi, Slunce, neutronovou hvězdu, naši Galaxii, černou díru, …

Vážení obrovských vesmírných objektů si ukážeme na Jupiteru, největší planetě Sluneční soustavy. Kolem Jupiteru obíhá mnoho měsíců, čtyři největší objevil dalekohledem vlastní konstrukce již v roce 1610 Galileo Galilei (a vyvrátil tak mýtus o tom, že je Země středem vesmíru). Říká se jim galileovské měsíce a jsou to Io, Europa, Ganymed a Callisto. Tyto měsíce obíhají kolem Jupiteru po téměř kruhových trajektoriích. Označíme-li

\(M_\mathrm{J}\) – hmotnost Jupiteru

\(r\) – poloměr kruhové trajektorie vybraného měsíce

\(T\) – dobu oběhu vybraného měsíce kolem Jupiteru

\(G\) – gravitační konstantu,

potom dle 3. Keplerova zákona platí

\[ \frac{r^3}{T^2} = \frac{GM_\mathrm{J}}{4\pi^2} \]

Gravitační konstantu známe, stačí tedy přímým pozorováním zjistit poloměr trajektorie a oběžnou dobu jednoho Jupiterova měsíce.

Jupiter se svými měsíci se pohybuje téměř ve stejné rovině, v níž obíhá také Země kolem Slunce (rovina ekliptiky). Při pozorování ze Země tedy nevidíme pohyb měsíců jako kruhový, nýbrž jako pohyb po úsečce. Maximální pozorovaná vzdálenost měsíce od středu Jupiteru je rovna poloměru trajektorie \(r\), doba, za níž se dostane z jedné extrémní polohy do téže extrémní polohy, je rovna periodě \(T\). Kvůli střídání dne a noci na pozemské observatoři nelze měsíc pozorovat trvale. Jeho zdánlivou vzdálenost od Jupiteru v závislosti na čase zaznamenáme do grafu, z něhož následně regresní analýzou určíme \(r\) a \(T\).

Reálné astronomické pozorování budeme simulovat pomocí programu JupLab.

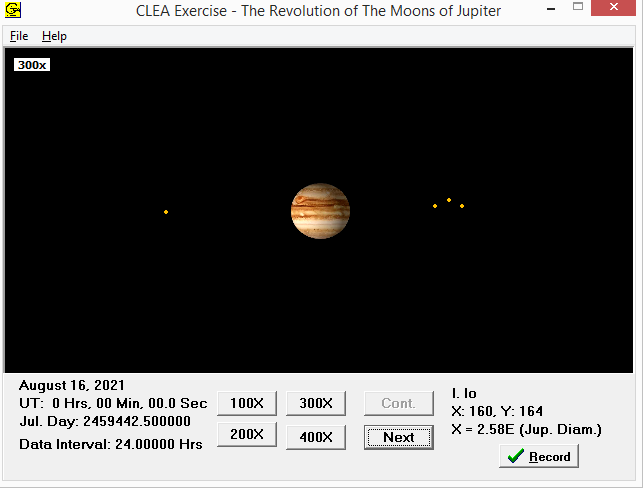
17.54 – Simulace pohybu Jupiterových měsíců.
Zdroj

Postup:

  1. Vyzkoušejte si základní ovládání programu: zvětšení, animace, barvy planet, pohled „shora“, nastavení kroku, …
  2. Po dobu 3 týdnů každou noc ve stejnou hodinu pozorujte polohu vybraného měsíce (nastavte krok pozorování 24 h a zaznamenávejte a ukládejte jeho polohu).
  3. V základní nabídce zvolte Data → Analyze…. V okně, které se tím otevře, vyberte pozorovaný měsíc.
  4. Vykreslenými body proložíme sinusoidu. Nejdříve zadáme přibližné startovací parametry fitování (zjistíte je v grafu odečtením „od oka“) Data → Plot → Fit sine curve → Set Initial Parameters…. V následujícím kroku pomocí posuvníků upravíte sinusoidu tak, aby co nejlépe „seděla“ k experimentálním bodům (hodnota RMS Residual – musí být co nejmenší). Program automaticky vypisuje parametry \(r\) a \(T\) zobrazované sinusoidy.
  5. Vypočítejte hmotnost Jupiteru \(M_\mathrm{J}\) a výsledek porovnejte se známou hodnotou.

Úkoly k zamyšlení:

  1. Zdůvodněte, proč při pohledu ze Země se nám jeví pohyb Jupiterových měsíců jako kmitavý po úsečce s harmonickým časovým průběhem čili proč máme naměřenými body prokládat právě sinusoidu.
  2. V použité simulaci se pohybovaly galileovské měsíce vodorovně. Jak to bude ve skutečnosti, až večer půjdete pozorovat oblohu dalekohledem?
  3. Pro šikovné: vymyslete způsob, jak zjistit a vyjádřit \(M_\mathrm{J}\) bez znalosti gravitační konstanty.
Poznámky pro učitele

Přihlášení: File → Log In…

Spuštění simulace: File → Run

Zobrazení: File → Features…

Parametry simulace: File → Timming…

Zaznamenání poloh měsíce: Kliknutím na měsíc se objeví jeho název a aktuální poloha, k zaznamenání použijte tlačítko Record. Tlačítkem Next se měsíc posune o zvolený pozorovací časový interval. Doporučujeme data průběžně ukládat File → Data → Save.

Analýza dat

Uložená data je možné znovu načíst File → Data → Load.

Otevření okna pro analýzu dat: Data → Analyze…

V tomto okně vybereme měsíc Data → Select Moon.

Na obrazovce se objeví graf s naměřenými hodnotami. Body vytvářejí část sinusoidy. Na ose \(x\) je čas (jednotkou jsou dny), na ose \(y\) vzdálenost měsíce od Jupiteru (jednotkou je průměr planety Jupiter). Zobrazenými body v grafu proložíme pomocí počítače co nejpřesněji sinusoidu. Postup při prokládání je následující:

  1. Aby byly body co nejvíce roztaženy na obrazovce, nastavíme v nabídce Plot → Set Data Span… počáteční den a dobu (10, 20, 30, 40 nebo 50 dní), která má být v grafu zobrazena.

  2. Při pohledu na graf zhruba odhadneme (od oka nebo pomocí myši)

    • počátek sinusoidy, tedy čas, kdy sinusoida protíná osu \(x\) a dále stoupá,
    • dobu jedné periody \(T\),
    • poloměr oběžné dráhy \(r\) = amplitudu sinusoidy.

    Tyto odhadnuté údaje vložíme do tabulky Plot → Fit Sine Curve → Set Initial Parameters…

  3. V grafu se objeví sinusoida, která pravděpodobně naměřenými body neprochází přesně. Pomocí tří posuvníků můžeme upravovat počáteční čas, periodu a poloměr trajektorie (amplitudu) tak, aby sinusoida co nejlépe procházela naměřenými body. Čím lepší je proložení sinusoidy, tím menší je hodnota červeného čísla RMS Residual.
  4. Pokud je již číslo RMS Residual nejmenší možné, přepneme na jemný posun (Slider sensitivity = Fine) a znovu zkusíme pomocí posuvníků ještě přesněji doladit sinusoidu – tedy snížit číslo RMS Residual.
  5. Po dosažení maximální přesnosti proložení sinusoidy odečteme vedle posuvníků přesnou hodnotu periody \(T\) a poloměru \(r\) (amplitudy). Tyto hodnoty poslouží k výpočtu hmotnosti Jupiteru.

Výpočet hmotnosti Jupiteru

1 rok = 365,2422 dní

průměr Jupiteru = 142 796 km

Úkol 3 pro šikovné

Třetí Keplerův zákon platí zřejmě i pro obíhání Země kolem Slunce, platí tedy

\[ \frac{r_\mathrm{Z}^3}{T_\mathrm{Z}^2} = \frac{GM_\mathrm{S}}{4\pi^2} \]

Vydělením rovnice pro Jupiter (v návodu pro žáky) touto rovnicí pro Slunce získáváme

\[ \frac{M_\mathrm{J}}{M_\mathrm{S}} = \frac{\displaystyle\left(\frac{r}{r_\mathrm{Z}}\right)^{\!3}}{\displaystyle\left(\frac{T}{T_\mathrm{Z}}\right)^{\!2}}\;, \]

kde \(r/r_\mathrm{Z}\) je poloměr trajektorie měsíce Jupiteru vyjádřený v astronomických jednotkách (au), \(T/T_\mathrm{Z}\) vyjadřuje periodu oběhu měsíce Jupitera v rocích a \(M_\mathrm{J}/M_\mathrm{S}\) je hmotnost Jupiteru vyjádřená v násobcích hmotnosti Slunce.

Poznamenejme závěrem, že \(1\ \mathrm{au}=149\,597\,870\ \mathrm{km}\) a \(M_\mathrm{S}=1{,}9891\cdot10^{30}\ \mathrm{kg}\).

Tlačítko pro návrat zpět nahoru na stránce (back to top)