Již od hlubokých prehistorických dob připisovali lidé velký význam nebeským tělesům a jejich pohybu na obloze. V pravidelnosti astronomických jevů, střídání ročních období, fází Měsíce, přeletech komet atd. spatřovali působení vyšších (božských) sil a bytostí. Tyto jevy měly i praktický význam při plánování zemědělských prací.
Počátky astronomie

Zdroj

Zdroj

Zdroj
První zmínky o astronomických pozorováních nacházíme v Číně, v Mezopotámii (zejména v Babylóně), v Egyptě a v Řecku. Mezi nejznámější starořecké astronomy patří učenci, o nichž jste pravděpodobně slyšeli již v jiných souvislostech: Thalés z Milétu, Pýthagorás ze Samu, Aristotelés, Hipparchos, Klaudios Ptolemaios. Vzhledem k tomu, že neměli téměř žádné astronomické vybavení – například dalekohled byl objeven až na přelomu 17. století – je fascinující, jak věrně dokázali jevy na obloze popsat a předvídat.
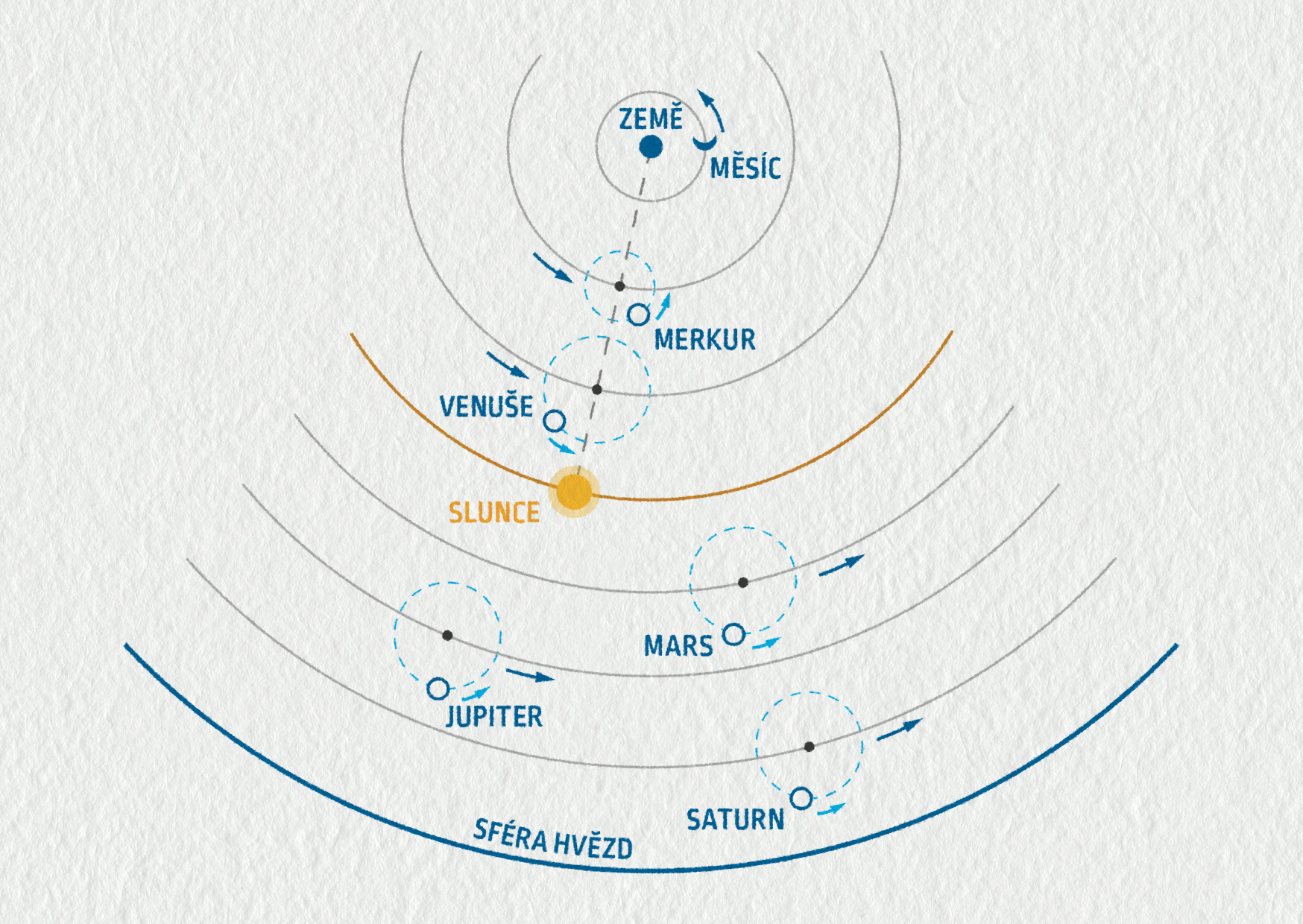
Starořímská civilizace a později evropský středověk přejímají Ptolemaiovu geocentrickou představu o uspořádání světa: ve středu vesmíru se nachází nehybná Země, kolem níž po kružnicích obíhají Měsíc a Slunce. Komplikovanější trajektorie planet při pozorování ze Země jsou vysvětlovány dodatečným pohybem po tzv. epicyklech.
Zdroj
Od roku 1543, kdy polský astronom Mikuláš Koperník publikuje své dílo De revolutionibus orbium coelestium (O obězích nebeských sfér), se mezi učenci postupně začíná prosazovat myšlenka heliocentrického uspořádání světa: středem vesmíru je Slunce, kolem něhož obíhají planety včetně Země. Ve své době čelila tato představa silnému odporu ze strany církve i mnoha vynikajících vzdělanců.

Zdroj
Nezastupitelnou roli v pochopení, jak Sluneční soustava ve skutečnosti „funguje“, má dánský astronom Tycho Brahe. Na observatoři Uranienborg na ostrově Hven, což je historicky první astronomická observatoř v západní Evropě, kterou pro něj nechal postavit dánský král Frederik II., prováděl v letech 1576–1597 pečlivá měření poloh planet. Ke sklonku života přijal pozvání císaře Rudolfa II., stal se jeho dvorním astronomem a na zámku v Benátkách nad Jizerou ve svých pozorováních pokračoval. Pochován je v kostele Panny Marie před Týnem na Staroměstském náměstí v Praze.

Zdroj
Na dvoře Rudolfa II. působil též německý matematik a astrolog Johannes Kepler. Na základě mimořádně systematických a pečlivě vedených Tychonových zápisků o měřeních Kepler po mnoho let propočítával trajektorie, rychlosti a oběžné doby pohybů planet, až dospěl k formulaci tří zákonů nesoucích dnes jeho jméno. Zajímavostí je, že Kepler sám trpěl krátkozrakostí a hvězdy patrně vůbec neviděl.

Zdroj
Keplerovy zákony pohybů planet ve Sluneční soustavě
První Keplerův zákon
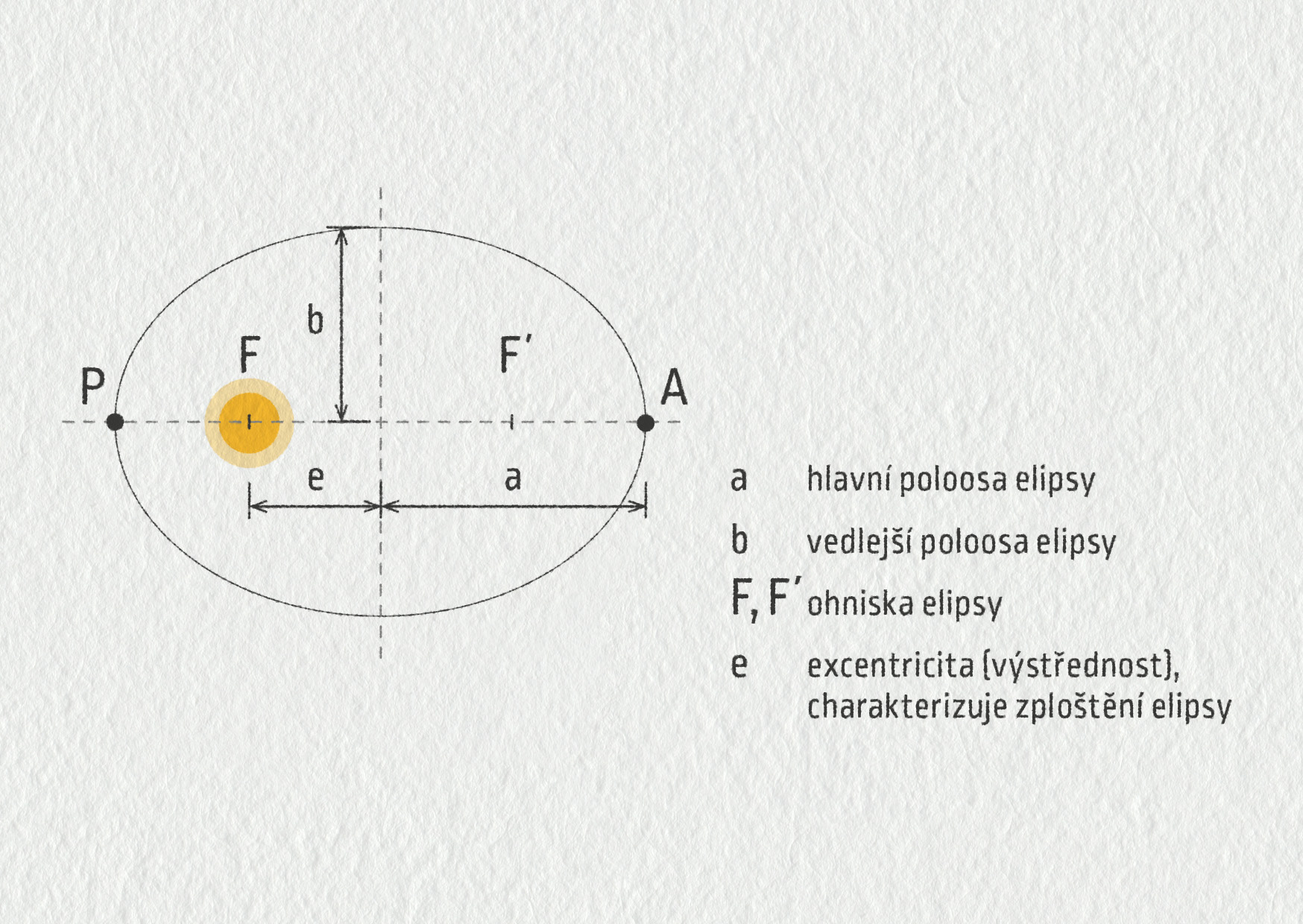
Planety obíhají po eliptických trajektoriích, v jejichž společném ohnisku je Slunce.
Zdroj
Elipsa patří mezi kuželosečky a studovat ji budete v matematice. Nakreslit si ji můžete velmi snadno, stačí upevnit konce provázku do ohnisek F a F', provázek pomocí hrotu tužky napnete a obtáhnete co největší obvod, který vám celková délka provázku „dovolí“.
Na trajektorii planety existují dva význačné body:
- P – perihelium čili přísluní – planeta je Slunci nejblíže, a
- A – afélium čili odsluní – planeta je od Slunce nejdále.
Pro trajektorii Země má hlavní poloosa a délku přibližně 150 milionů kilometrů. Tato délka se nazývá astronomická jednotka au, tedy přesně 1 au = 149 597 870,7 km. Výstřednost trajektorie Země je \(e=2\,500\,000\ \mathrm{km}\) čili vychýlení Slunce ze středu elipsy představuje jen 1,7 % délky hlavní poloosy.
Kružnice je speciálním případem elipsy s výstředností \(e=0\), kdy ohniska splývají s jejím středem. Z číselných údajů pro Zemi můžeme usoudit, že její trajektorie se jen velmi málo liší od kružnice, že tedy pohyb Země můžeme kruhovým pohybem v prvním přiblížení modelovat. Podobný závěr lze provést i pro ostatní planety Sluneční soustavy.
Druhý Keplerův zákon
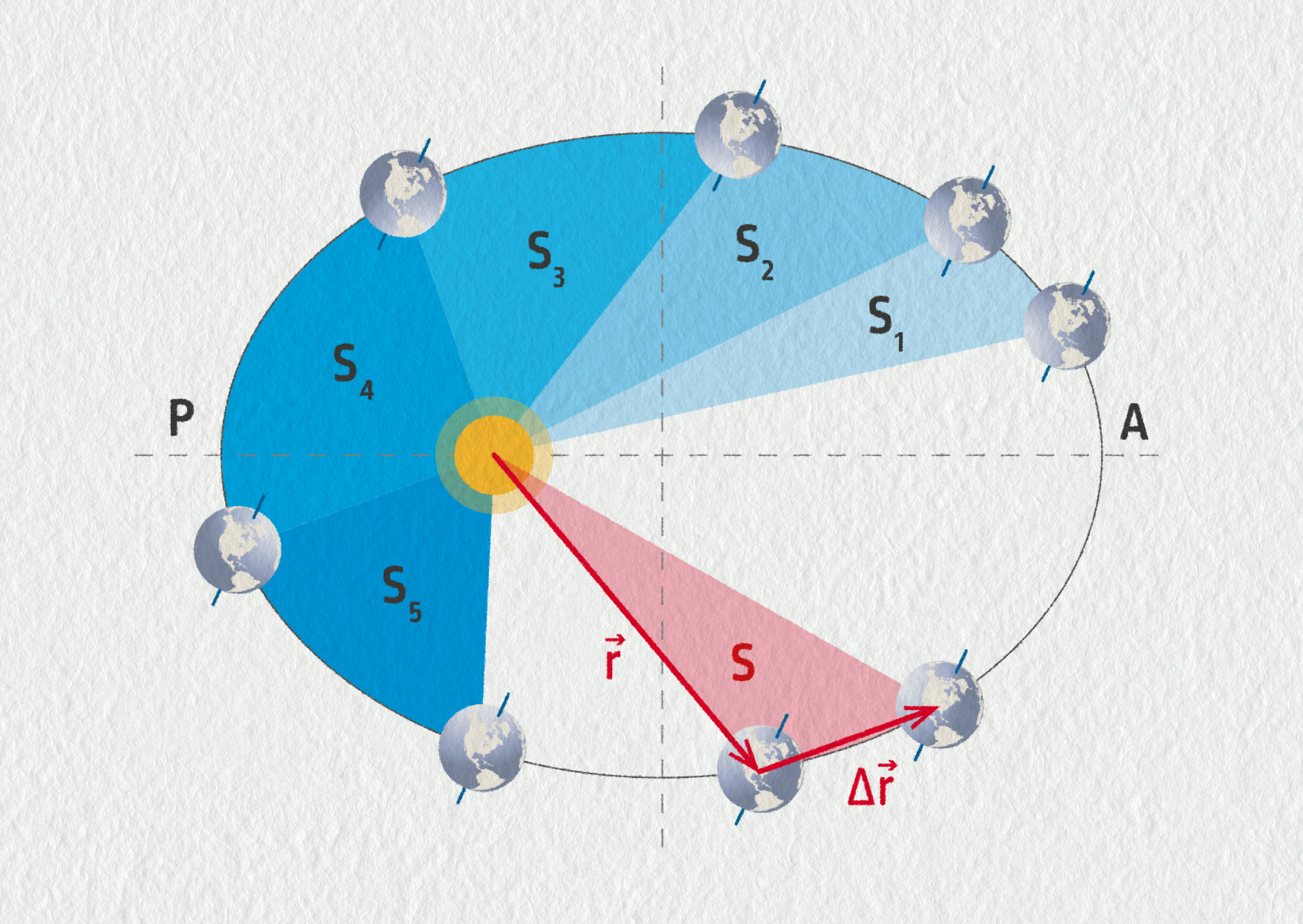
Obsah plochy opsané průvodičem planety za jednotku času je stálý.
Zdroj
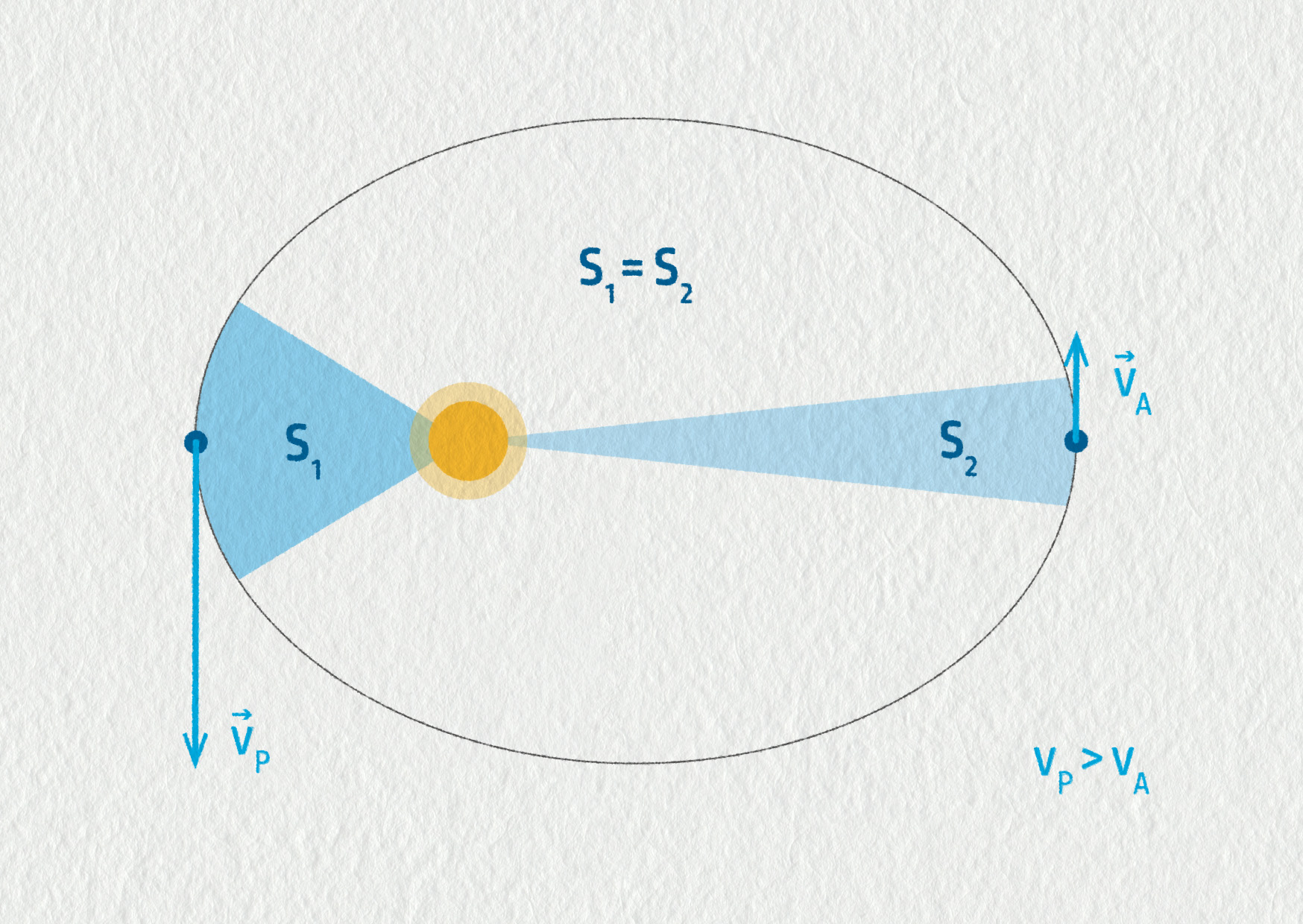
Průvodič planety je spojnice Slunce a dané planety. Je to vlastně polohový vektor planety \(\Vec{r}\) v heliocentrické vztažné soustavě. Druhý Keplerův zákon říká, že za určitou dobu (např. jeden měsíc) opíše průvodič vždy stejnou plochu. Z toho vyplývá, že na eliptické trajektorii se nemůže planeta pohybovat stále stejně rychle. Jak ukazuje následující obrázek, jsou-li plochy \(S_1\) a \(S_2\) opsané za stejný čas \(\Delta t\) stejné, musí se planeta v periheliu pohybovat rychleji než v aféliu, neboť za \(\Delta t\) urazí v okolí perihelia delší dráhu než za stejný čas v okolí afélia.
Zdroj
Třetí Keplerův zákon
Podíl třetí mocniny hlavní poloosy eliptické trajektorie \(a\) a druhé mocniny oběžné doby \(T\) je stejný pro všechny planety Sluneční soustavy.
\[ \frac{a^3}{T^2} = \hbox{konst.} \]Znamená to tedy, že oběh planety vzdálenější od Slunce trvá déle než oběh planety bližší. Jak ukážeme v podkapitole Pohyb družic, konstanta v uvedeném zákoně závisí na hmotnosti centrálního tělesa (Slunce), a tedy tento zákon lze použít ke „zvážení“ onoho tělesa.
Přímým pozorováním lze zjistit, že oběžná doba Marsu kolem Slunce je 687 dní. Určete jeho vzdálenost od Slunce.
Oběžnou dobu Marsu označíme symbolem \(T_\mathrm{M}\). Mars se pohybuje po eliptické trajektorii, jeho vzdálenost od Slunce se během pohybu mění. Jelikož je zploštění elipsy malé, bude délka jeho hlavní poloosy \(a_\mathrm{M}\) dobrým odhadem střední vzdálenosti od Slunce.
Podle třetího Keplerova zákona je podíl \(a^3/T^2\) konstantní a stejný pro všechny planety. Musí tedy být roven analogickému podílu pro Zemi
\[ \frac{a_\mathrm{M}^3}{T_\mathrm{M}^2} = \hbox{konst.} = \frac{a_\mathrm{Z}^3}{T_\mathrm{Z}^2} \]Parametry oběhu Země známe: \(a_\mathrm{Z}=1\ \mathrm{au}\) a \(T_\mathrm{Z}=1\ \hbox{rok}=365\ \hbox{dní}\). Odtud po matematické úpravě dostáváme výsledek
\[ a_\mathrm{M} = \left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^{2/3} a_\mathrm{Z} = \left(\frac{687\ \hbox{dní}}{365\ \hbox{dní}}\right)^{2/3}\cdot1\ \mathrm{AU} = 1{,}52\ \mathrm{au} = 2{,}27\cdot10^8\ \mathrm{km} \]Pohyby planet jsou elegantně jednoduché z hlediska heliocentrické vztažné soustavy. Při pozorování planet z povrchu Země je jejich pohyb mnohem složitější:
- Během noci planety vycházejí nad a zapadají pod horizont kvůli otáčení Země kolem její osy a náklonu této osy. Na obloze neopisují jednoduché trajektorie.
- Kvůli vlastnímu pohybu Země kolem Slunce vykazují vnější planety zdánlivý retrográdní pohyb, tj. ve svém postupu na pozadí vzdálených hvězd se v určitý okamžik zastaví, pak určitou dobu couvají, než se opět dají do pohybu obvyklým směrem. Tato zvláštnost byla známa již v antice: samotné slovo planeta má původ v řeckém πλανήτης, což znamená tulák. Kvůli těmto „toulavým hvězdám“ musel Ptolemaios ve svém modelu uměle zavést epicykly.
- Frankofonním čtenářům doporučujeme toto velice pěkně zpracované video o pohybech planet ve Sluneční soustavě: https://www.youtube.com/watch?v=0cOvmotwndE&t=1s. Retrográdní pohyb je vysvětlován od času 4:50.
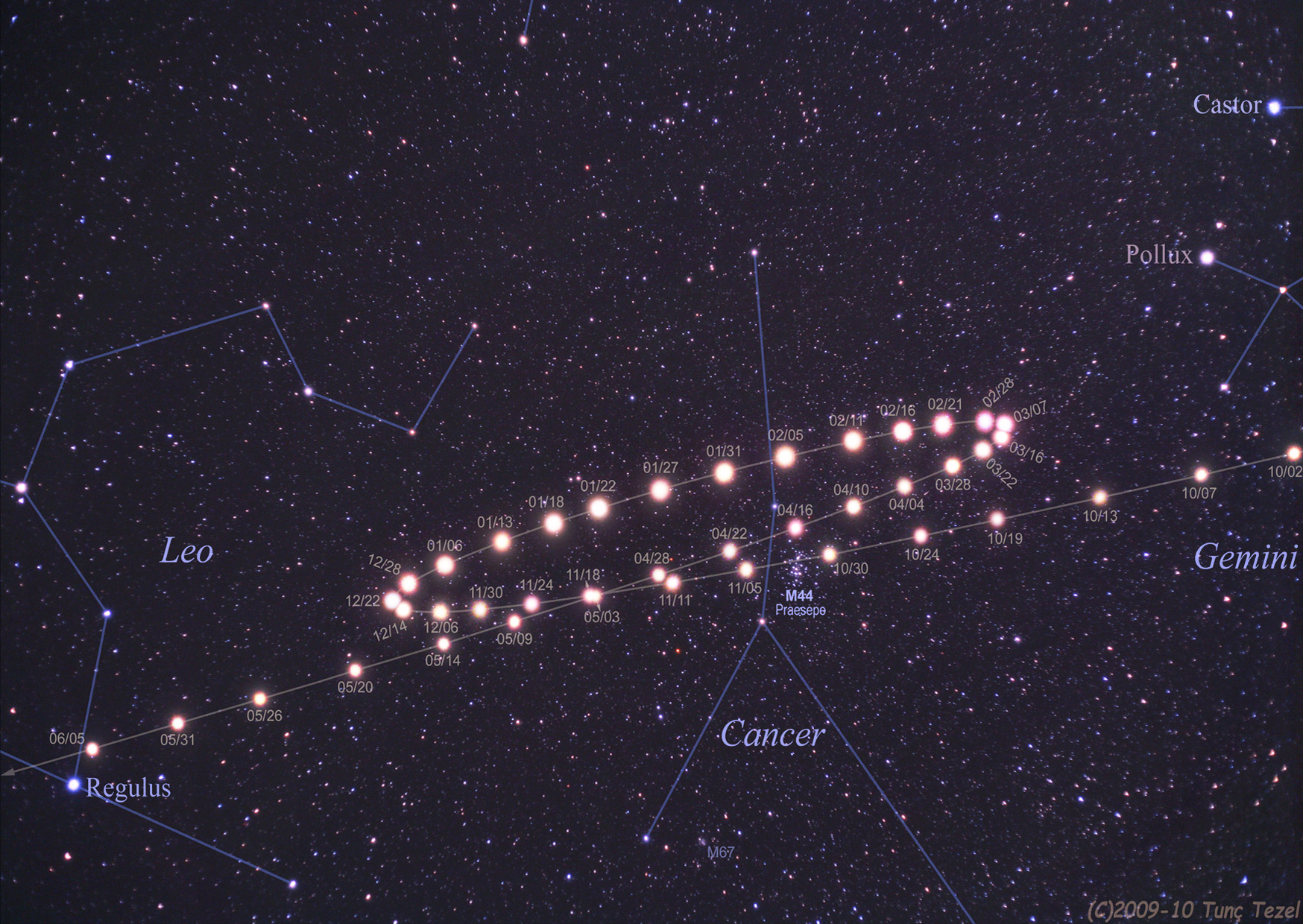
Zdroj
Hledáme matematické vyjádření druhého Keplerova zákona.
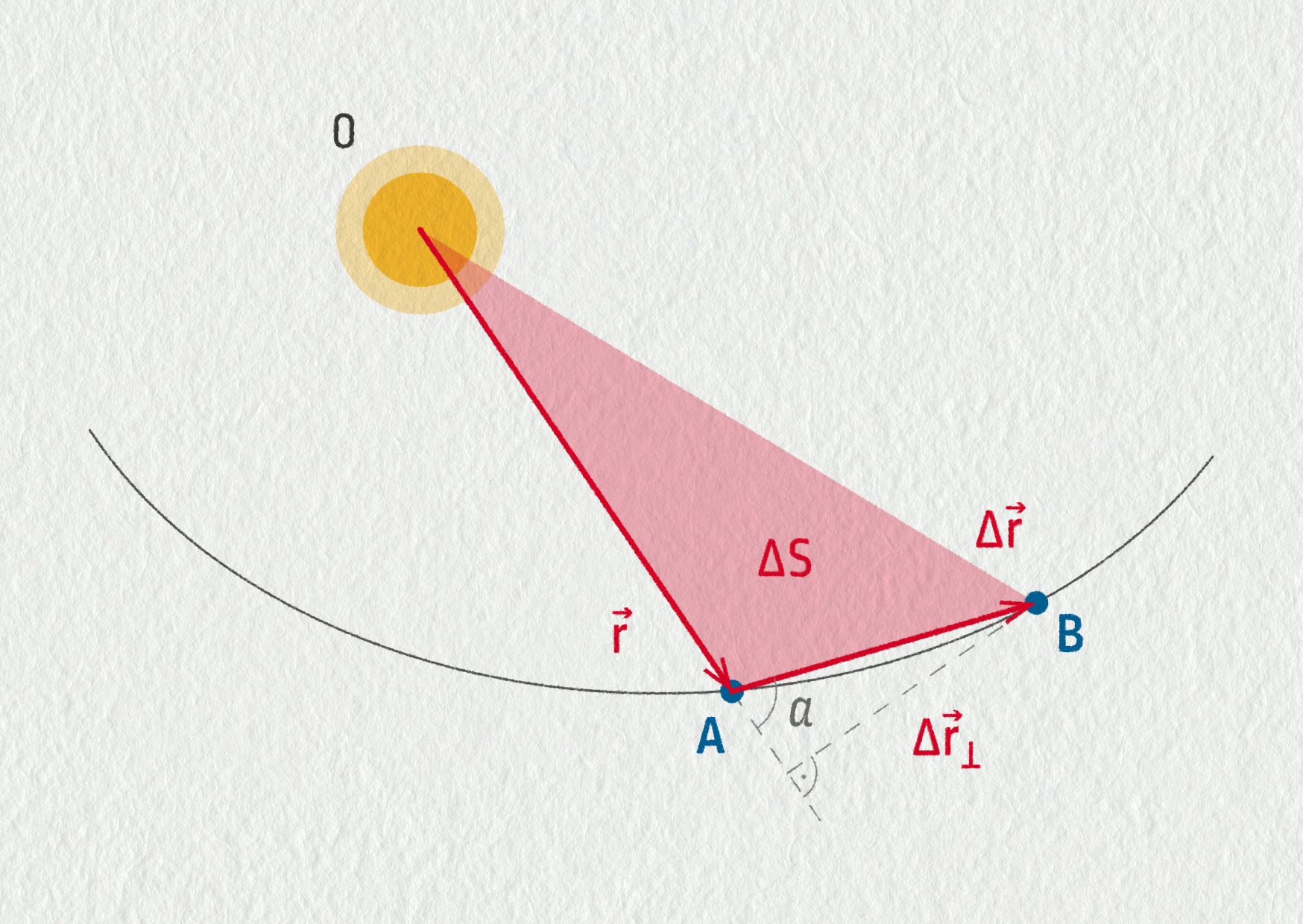
Situace je znázorněna na obrázku 17.15. Slunce se nachází v bodě O. Předpokládejme, že za čas \(\Delta t\) se planeta posune o vektor \(\Delta\Vec{r}\) z bodu A do bodu B. Opíše při tom plochu \(\Delta S\). Čím kratší bude interval \(\Delta t\), tím lépe můžeme nahradit oblouk AB úsečkou, a tím více se bude velikost plochy \(\Delta S\) blížit obsahu trojúhelníka OAB. Plochu tohoto trojúhelníka zapíšeme jako
\[ \Delta S = \frac{1}{2} r\cdot\Delta r_\bot = \frac{1}{2}r\cdot\Delta r\cdot\sin\alpha\;. \]K ploše tohoto trojúhelníka se můžeme dobrat ještě elegantněji pomocí vektorového součinu
\[ \Delta S = |\Delta\Vec{S}| = \left|\frac{1}{2}\Vec{r}\times\Delta\Vec{r}\right| \]Má tedy smysl definovat plošnou rychlost planety jakožto (orientovanou) plochu za čas předpisem
\[ \Vec{w} = \frac{\Delta\Vec{S}}{\Delta t} = \frac{\frac{1}{2}\Vec{r}\times\Delta\Vec{r}}{\Delta t} = \frac{1}{2}\Vec{r}\times\Vec{v} \]Podle 2. Keplerova zákona je plošná rychlost planety \(\frac{1}{2}\Vec{r}\times\Vec{v}\) konstantní.
Zdroj
Ve skutečnosti není Slunce v prostoru nijak fixované. S danou planetou obíhá kolem společného těžiště (v případě Slunce a Země leží toto těžiště uvnitř objemu Slunce). Průvodič planety je přesněji spojnice těžiště této dvoučásticové soustavy a dané planety. Situace se ještě více komplikuje přítomností dalších planet.
Výraznou ránu geocentrickému chápání světa zasadil italský učenec Galileo Galilei. V roce 1610 poprvé pomocí dalekohledu vlastní konstrukce spatřil Jupiterovy měsíce. Nejprve si myslel, že se jedná o hvězdy, ale záhy poznal, že se tato tělesa pohybují kolem Jupitera. V dalekohledu pozoroval také fáze Venuše – ano, podobně jako Slunce ozařuje polovinu povrchu Měsíce, i planeta Venuše je z poloviny osvícena slunečními paprsky, a při různých vzájemných polohách Slunce, Venuše a Země vidíme ze Země pokaždé jiný díl této osvětlené plochy. Tím prokázal, že existují nebeské objekty, které neobíhají kolem Země, a že tedy Země nemusí mít ve vesmíru výsadní postavení, nemusí být středem vesmíru.
Životní příběh Galilea Galileiho není jen o objevování fyzikálních poznatků, ale také zápasem mimořádného člověka o svobodu hledat pravdu a říkat ji nahlas.

Zdroj
Co byste odpověděli člověku, který se vytasí s následujícím pohledem na věc?
„A proč by se Země měla pohybovat? Když si lehnu do trávy, země se ani nehne, žádný pohyb necítím. Vzduch mě jen zlehka ovívá, ale vím, že je to větrem, ten proudí kolem země a někdy je úplné bezvětří. Nějaký chlapík, co žil před čtyřmi sty lety? Kdo ví, co v dalekohledu vůbec viděl! Já cítím pevnou půdu pod nohama, ať mi nikdo nic nevykládá!“
Můžete jej v tom klidně nechat a neříkat mu nic. Bude žít šťastně až do smrti:)
- Díky kožním receptorům tlaku, receptorům napětí ve svalech, šlachách a kloubních pouzdrech a zejména díky vestibulárnímu ústrojí vnitřního ucha vnímá člověk vše, co vyvolává tlaky a napětí v těle – například přítomnost gravitačního pole, zrychlování v autě, otřesy (což je nepravidelné zrychlování tam a zpět), proud větru kolem těla… Naopak klid a rovnoměrný přímočarý pohyb jsou nerozlišitelné. V začátcích železniční dopravy před dvěma sty lety se lidé obávali, jestli je velká rychlost 80 km/h při cestování nezabije. Ukazuje se, že rychlost samotná nikoli, ovšem velké zrychlení při nárazu do překážky ano.
- Kolem Slunce se Země pohybuje s dostředivým zrychlením 6 ⋅ 10−3 m/s2, které je 1650 krát menší než tíhové zrychlení \(g=9{,}81\ \mathrm{m/s}^2\). Obíhání je příliš slabý podnět, aby je tělo podrobené zemské gravitaci zaregistrovalo. Proto obíhání nemůžeme pocítit.
- Přímo na Zemi pozorovatelný experimentální důkaz otáčení zeměkoule vymyslel a uskutečnil teprve v roce 1851 Léon Foucault. Přestože v 19. století byla rotace naší planety z nepřímých důkazů známa, způsobil velkou senzaci jak v odborných kruzích, tak u široké veřejnosti. Vysvětlení tohoto experimentu najdete ve 21. kapitole.

Zdroj
Navzdory experimentálním důkazům vám možná intuice říká, že k všeobecnému přijetí heliocentrického modelu zde ještě něco chybí. Ano, chybí tu uspokojivé vysvětlení, chybí pochopení, proč by uspořádání světa mělo vypadat tak, jak si je představoval Koperník. Zajímá vás, jak to je ve skutečnosti? Tak čtěte dál.

