Vrhy

Ze značně velké výšky pustíme bez počáteční rychlosti malý, ale těžký kamínek.

1. Jakou dráhu urazí za 1 sekundu? za 2 sekundy? za 3 sekundy?
2. Jakou dráhu urazí během druhé sekundy pohybu?
3. Jakou dráhu od vypuštění urazil v okamžiku, kdy je jeho rychlost 15 m/s?

Za jak dlouho a jakou rychlostí dopadne na zem předmět z výšky 10 m? Předpokládáme, že počáteční rychlost je nulová.

Z výšky 20 m hodíme svisle dolů malý těžký předmět rychlostí 5 m/s.

1. Jaká bude jeho rychlost 1 sekundu po vyhození?
2. Jakou dráhu urazil během první sekundy?
3. Za jak dlouho dopadne na zem?
4. Jakou rychlostí dopadne na zem?

Ze země vymrštíme předmět svisle vzhůru rychlostí 30 m/s.

1. Jaká bude rychlost předmětu a výška nad zemí 2 sekundy po vymrštění?
2. Jaká bude rychlost předmětu a výška nad zemí 5 sekund po vymrštění?
3. V jakém čase se předmět dostane do maximální výšky?
4. Do jaké maximální výšky vystoupí?
5. Jakou rychlostí dopadne na zem a za jak dlouho?

Ve výšce 4 m nad zemí hodíme svisle nahoru balón rychlostí 5 m/s.

1. Za jak dlouho a do jaké maximální výšky nad zem vyletí?
2. Za jak dlouho od vyhození a jakou rychlostí proletí kolem nás směrem dolů?
3. Za jak dlouho od vyhození a jakou rychlostí dopadne na zem?

Házíme teď předmět vodorovně z výšky 10 m rychlostí 5 m/s.

1. Za jak dlouho dopadne těleso na zem?
2. V jaké vodorovné vzdálenosti od místa vrhu?
3. Jakou rychlostí dopadne na zem?
4. Jaká bude výška a rychlost tělesa 1 sekundu po vyhození?

Házíme znovu předmět vodorovně ve výšce 10 m. Jakou rychlostí musíme hodit, aby dopadl ve vodorovné vzdálenosti 10 m?

Házíme předmět vodorovně ve výšce 20 m.

1. Jakou rychlostí musíme hodit, aby dopadl ve vodorovné vzdálenosti 20 m?
2. Jakou rychlostí v tomto případě dopadne na zem?
3. Pod jakým úhlem dopadne na zem?

Kámen vržený vodorovně rychlostí 10 m/s dopadl ve vzdálenosti 15 m. V jaké výšce byl vržen? Pod jakým úhlem dopadne na zem?

Jakou rychlostí musíme ve výšce 15 m vodorovně hodit těleso, aby dopadlo na zem rychlostí 25 m/s?

Ze země odkopneme balón rychlostí 30 m/s pod úhlem 45°.

1. Za jak dlouho dopadne na zem?
2. V jaké vzdálenosti dopadne na zem?
3. Jakou rychlostí dopadne na zem?
4. Pod jakým úhlem dopadne na zem?

Ze země odpálíme golfový míček rychlostí 50 m/s pod úhlem 30°. Vypočítejte

1. x-ovou a y-ovou složku počáteční rychlosti,
2. vodorovnou a svislou dráhu, kterou urazí za 1 sekundu,
3. dobu pádu a vzdálenost dopadu od místa vrhu,
4. čas, kdy vystoupí do nejvyššího bodu, a maximální výšku,
5. rychlost v nejvyšším bodě a rychlost dopadu.

Jakou rychlostí bychom museli odpálit golfový míček pod úhlem 30°, aby dopadl ve vzdálenosti 50 m?

Golfový míček byl odpálen pod úhlem 20° rychlostí 25 m/s. Je možné, abychom trefili lampu na hřišti ve výšce 4 m nad zemí?

Balón odkopnutý od branky pod úhlem 50° dopadl ve vzdálenosti 60 m. Jaká je počáteční rychlost balónu? Do jaké maximální výšky vystoupil? Pod jakým úhlem dopadne na zem?

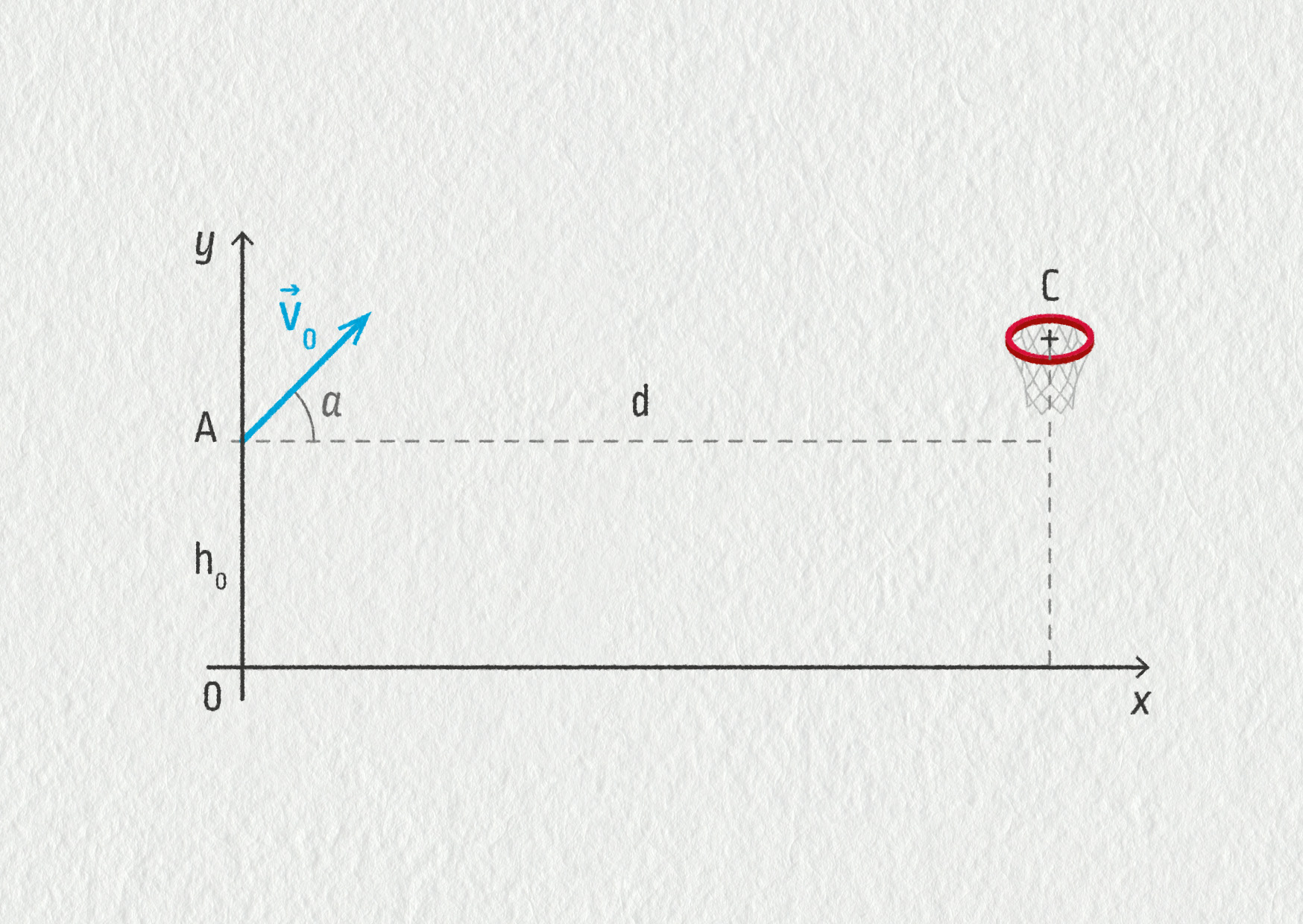
Abychom dali v basketbalu koš, musí míč projít kovovým kruhem, který je umístěn ve vodorovné rovině 3,05 m od vodorovné podlahy. Pro zjednodušení úlohy předpokládejme, že je míč hmotný bod a že musí projít přesně bodem C, který se nachází ve středu kovového kruhu.

Z bodu A, který se nachází 2,0 m nad podlahou, hází basketbalista míč rychlostí \(v_0\). Vektor rychlosti svírá s vodorovnou rovinou úhel \(\alpha=45^\circ\).

1. Sestavte časové rovnice pohybu.
2. Určete rovnici trajektorie míče v soustavě souřadnic (O, x, y).
3. Jaká musí být hodnota rychlosti míče, aby byl hod úspěšný (body A a C jsou od sebe vzdáleny 7,1 m ve vodorovném směru)?

Atlet hází koulí o hmotnosti \(m=7{,}25\ \mathrm{kg}\). Toto těleso je vrženo z výšky \(h=1{,}70\ \mathrm{m}\) vzhledem k zemi s rychlostí \(\Vec{v}_0\), jejíž vektor svírá s vodorovným směrem úhel \(\alpha=15^\circ\). Velikost počáteční rychlosti má hodnotu \(v_0=15\ \mathrm{m/s}\). Předpokládáme, že pohyb koule není ovlivněn třením se vzduchem.

1. Sestavte časové rovnice pohybu.
2. Určete rovnici trajektorie hmotného středu koule v kartézské soustavě souřadnic s vhodně vybraným počátkem.
3. Koule dopadne na zem v bodě P. „Dostřelem“ \(x_P\) nazýváme x-ovou souřadnici bodu P. Spočítejte velikost \(x_P\).

Tenistka při podání nadhazuje míček o hmotnosti \(m=58\ \mathrm{g}\) svisle vzhůru. Počáteční rychlost míčku je \(v_0=5{,}4\ \mathrm{m/s}\). Jak dlouho bude míček stoupat? Jaké maximální výšky dosáhne? Jakou bude mít rychlost těsně před tím, než ho svou raketou zasáhne ve výšce 2,7 m nad povrchem kurtu?

Kulička, kterou pokládáme za hmotný bod, je vržena do vzduchu. Odpor vzduchu zanedbáváme. Pohyb kuličky byl zachycen na fotografii pomocí vhodně nastaveného fotoaparátu. Přiložený obrázek je fotografií roviny, ve které se kulička pohybuje. Zvětšení této fotografie je konstantní poměr mezi vzdálenostmi na fotografii a odpovídajícími vzdálenostmi ve skutečnosti. Na fotografii není zachycen ani vodorovný ani svislý směr.

Během pohybu byla kulička osvětlena elektronickým bleskem, které vytvářel intenzivní záblesky světla každých 10 ms. Následující dokument znázorňuje jednotlivé polohy kuličky na fotografii bez dalšího zmenšení nebo zvětšení.

1. Sestrojte na dokumentu vektory rychlosti \(\Vec{v}_3\) a \(\Vec{v}_5\), které znázorňují rychlost obrazu kuličky v bodech A₃ a A₅. Vhodné měřítko: 1 cm pro 0,4 cm/s.
2. Vypočítejte velikost zrychlení kuličky v bodě A₄ a tento vektor znázorněte na obrázku. Doporučené měřítko 1 cm pro 10 m/s².
3. Za předpokladu, že se kulička pohybuje volným pádem, a má tudíž konstantní zrychlení, určete zvětšení \(Z\) fotografie. (Vektor tíhového zrychlení \(\Vec{g}\) má směr svislý dolů a jeho velikost je \(g=9{,}8\ \mathrm{m/s^2}\).)
4. V bodě A₄ narýsujte dvě osy. První horizontální a druhou vertikální.
5. Ukažte, že horizontální složky vektoru rychlosti jsou konstantní.
6. Za předpokladu, že kulička byla vržena vodorovně, určete velikost počáteční rychlosti \(v_0\).