Vodorovný pohyb
Podívejme se nejprve na situaci, kdy pomocí lana táhneme stálou rychlostí těleso po vodorovné podložce (viz obrázek 15.8). Jestliže táhneme lano silou o velikosti \(F\) pod úhlem \(\alpha\), jak velké jsou třecí síla a kolmá tlaková síla?
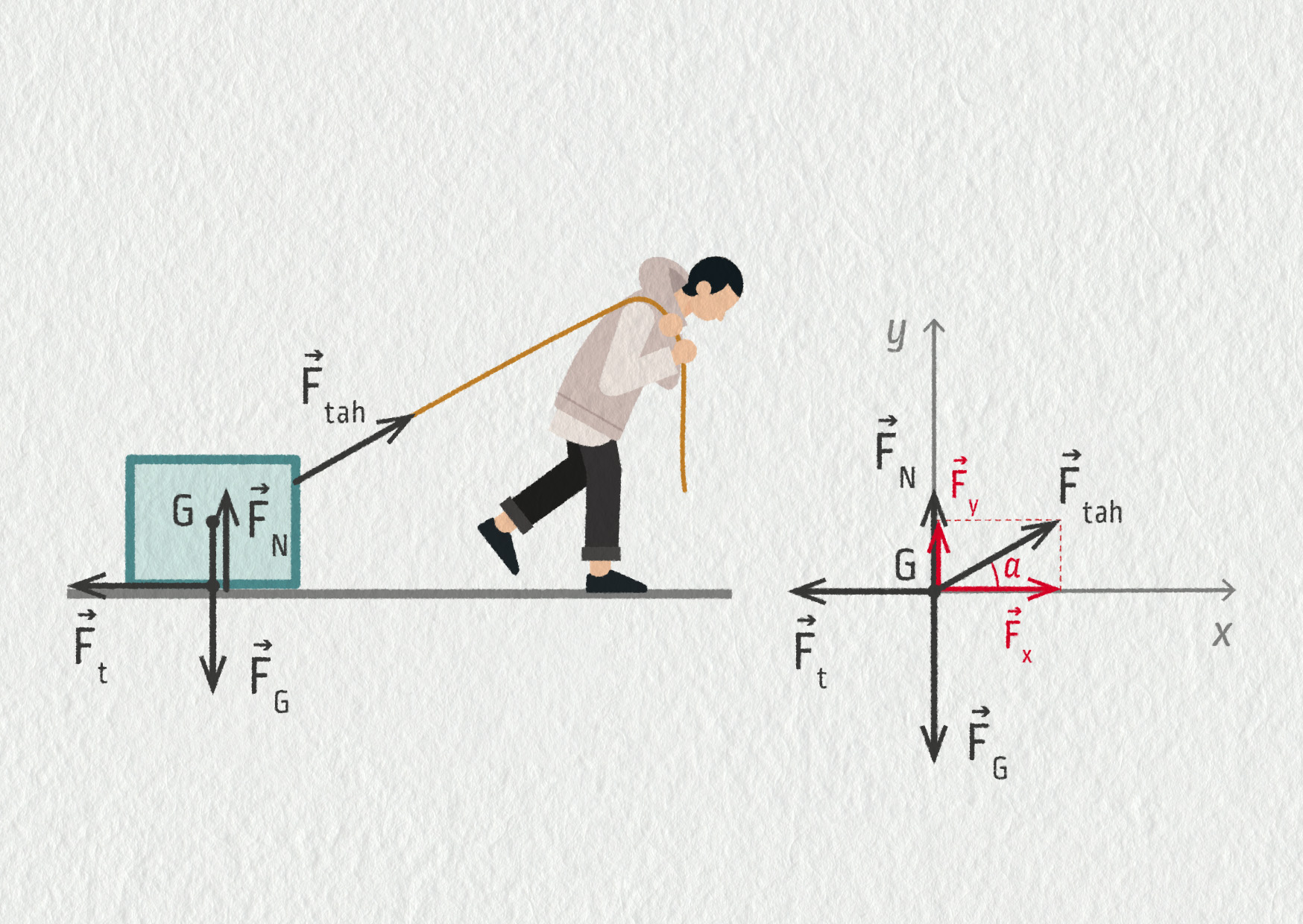
Zdroj
Podle prvního Newtonova zákona víme, že v případě pohybu rovnoměrného přímočarého se všechny síly působící na těleso navzájem vyruší. Můžeme tedy tento zákon zapsat ve vektorové podobě následujícím způsobem:
\[ \Vec{F}_\mathrm{tah}+\Vec{F}_\mathrm{t}+\Vec{F}_\mathrm{G}+\Vec{F}_\mathrm{N}=\Vec{0}\;. \]Síly však působí různými směry. Jak můžeme vypočítat jejich velikosti? Zvolme si nejprve kartézskou souřadnicovou soustavu, ve které přejdeme od jedné vektorové rovnice ke dvěma skalárním. Zvolme osu \(x\) ve směru pohybu. Zde tedy vodorovnou. Osa \(y\) je k ní kolmá, kladný směr volme směrem vzhůru. Vidíme, že tři ze čtyř sil působí ve směru souřadnicových os, pouze tažná síla \(\Vec{F}_\mathrm{tah}\) působí pod úhlem \(\alpha\) vzhledem k vodorovné rovině, vzhledem ke směru osy \(x\). Průměty sil, a stejně tak jakýchkoliv jiných vektorů, hledáme tak, že se podíváme na silový diagram a porovnáváme jejich směr se směrem souřadnicových os. Pokud síla působí v kladném směru dané osy, zapíšeme jako zde \(+F_\mathrm{N}\) ve směru osy \(y\). Pokud působí v záporném směru dané osy, zapíšeme jako zde \(-F_\mathrm{G}\). Jestliže je síla kolmá na danou osu, je její průmět v tomto směru nulový (viz třecí síla \(F_\mathrm{t}\) ve směru svislém). Celkem tedy dostáváme ve směru obou os dvě rovnice:
\[ \begin{aligned} x\colon&& F_x - F_\mathrm{t} + 0 + 0 &= 0\\ y\colon&& F_y + 0 + F_\mathrm{N} - F_\mathrm{G} &= 0\\ \end{aligned} \]Pro velikosti složek tahové síly \(\Vec{F}_\mathrm{tah}\) platí
\[ \begin{aligned} F_x &= F_\mathrm{tah}\cos\alpha\;,\\ F_y &= F_\mathrm{tah}\sin\alpha\;,\\ \end{aligned} \]proto pro velikost třecí síly získáváme \(F_\mathrm{t}=F_x=F_\mathrm{tah}\cos\alpha\). Z druhé rovnice pak vyjádříme velikost kolmé tlakové síly pomocí \(F_\mathrm{N}=F_\mathrm{G}-F_y=F_\mathrm{G}-F_\mathrm{tah}\sin\alpha\).
Ukázali jsme si postup, který ještě mnohokrát využijeme. Jestliže síly nepůsobí stejným směrem, zapíšeme Newtonovy zákony ve složkách jednotlivých souřadnicových os.
Na následujícím obrázku jsou znázorněny dvě síly. Určete pro každou z nich jejich složky ve směru os soustavy souřadnic. Velikosti sil i jejich složek jsou v N (1 dílek znázorňuje 1 N). Uvádějte hodnotu včetně jednotky.

Zdroj
Na následujícím obrázku jsou znázorněny dvě síly. Určete pro každou z nich jejich složky ve směru os soustavy souřadnic. Velikosti sil i jejich složek jsou v N (1 dílek znázorňuje 1 N).
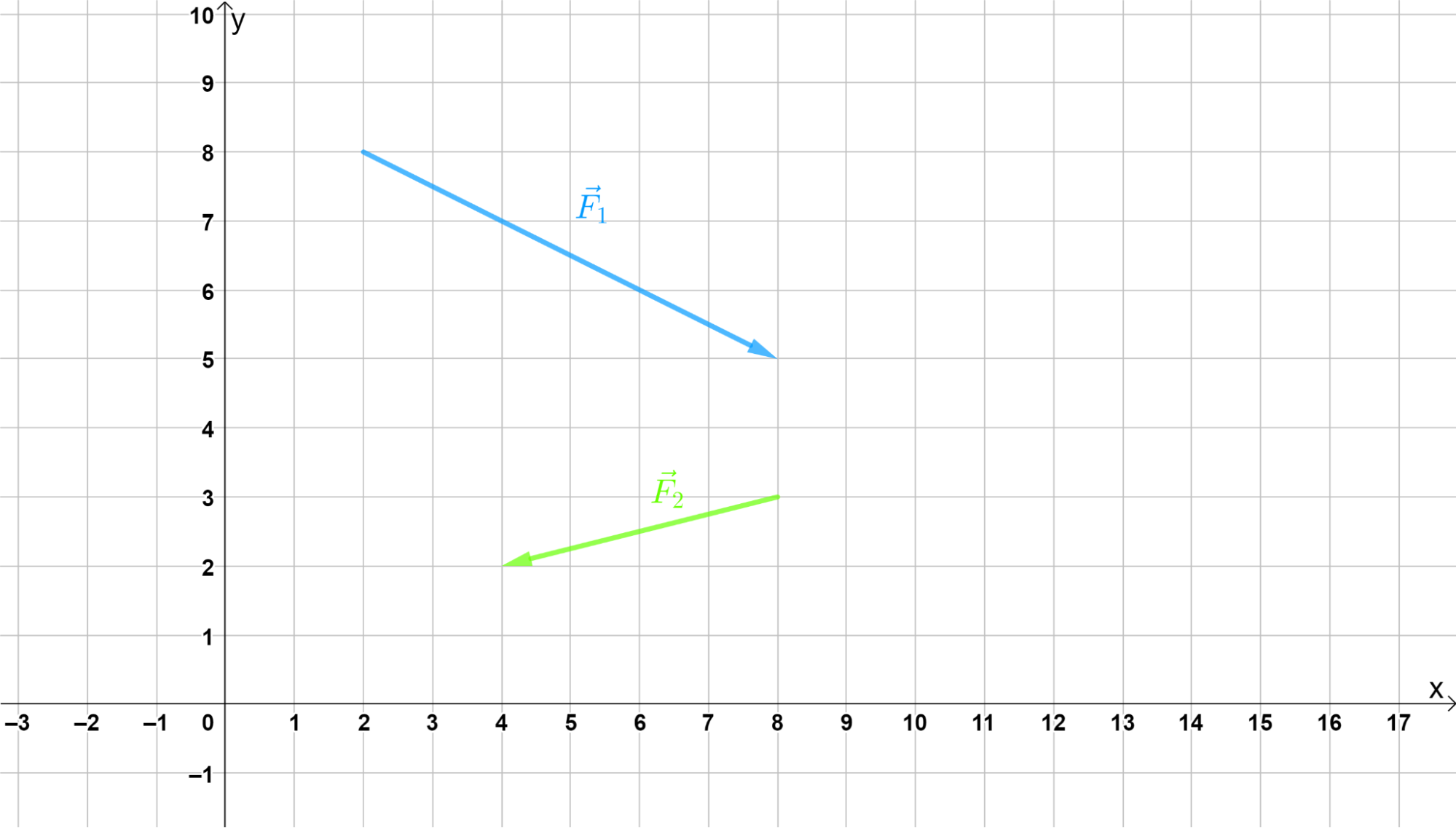
Zdroj
Na následujícím obrázku jsou znázorněny dvě síly. Určete pro každou z nich jejich složky ve směru os soustavy souřadnic. Velikosti sil i jejich složek jsou v N (1 dílek znázorňuje 1 N).
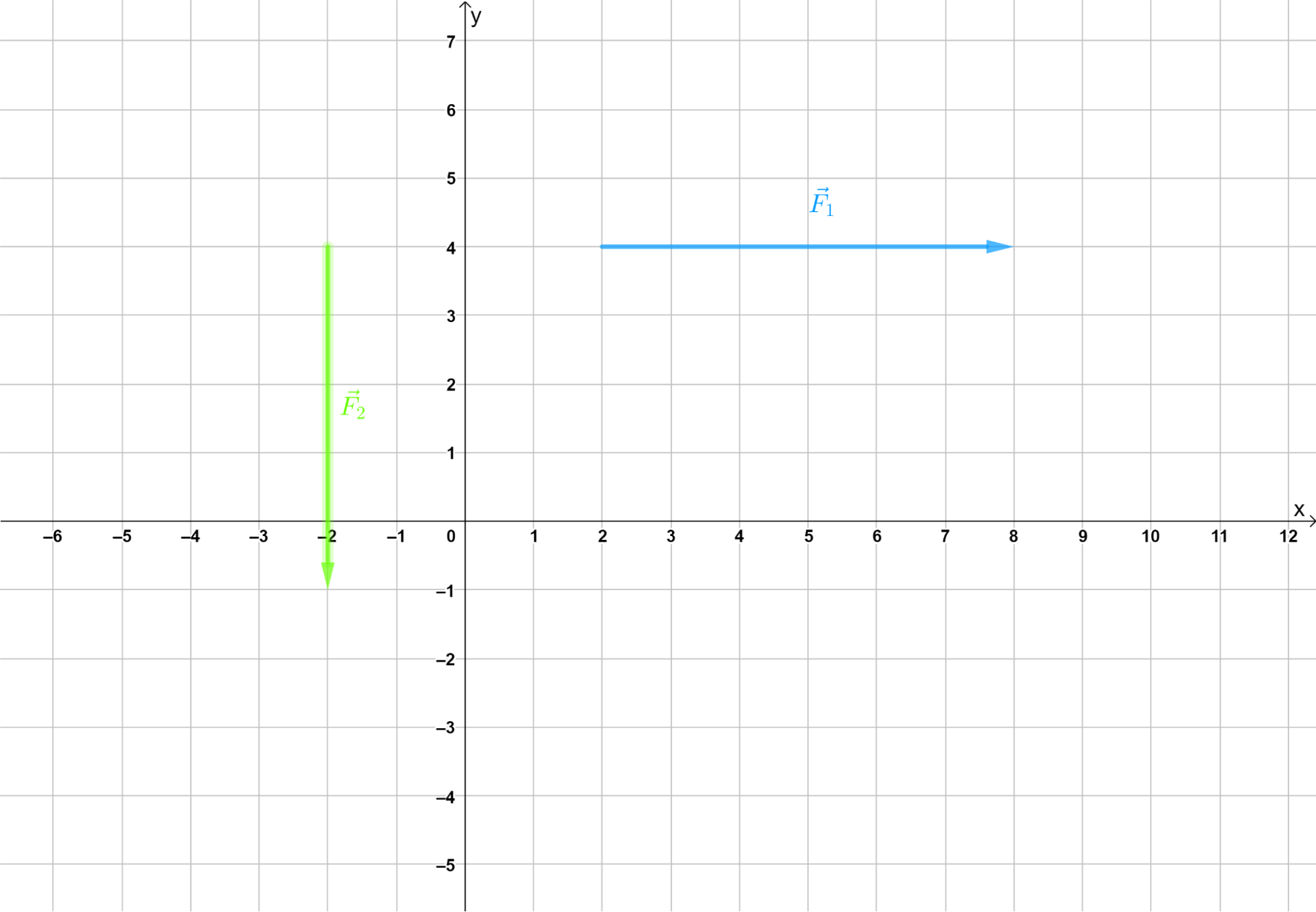
Zdroj
V předchozí úvaze jsme znali pohyb tělesa a odvozovali z něj velikosti působících sil. Newtonovy zákony však lze použít i obráceně. Dokážeme-li určit síly, které na těleso působí, můžeme z nich odvodit pohybový stav tělesa a předvídat jeho další vývoj.
Nakloněná rovina
Začněme tím, co dobře známe – lyžováním, sáňkováním nebo jízdou na kole. Sjíždíme kopec, pro nás fyziky nakloněnou rovinu, a rychlost narůstá. Co je příčinou zrychlování? Bude rychlost narůstat neustále, nebo dosáhneme po určité době maximální velikosti? Pro jednoduchost nahrazujeme zakřivený svah nakloněnou rovinou.
I když se může problém zdát složitý, jde stále jen o pohyb v jednom směru, ve směru svahu, na kterém lyžujeme (ve směru nakloněné roviny). Proto i volba souřadnicového systému je trochu specifická. Kladný směr osy \(x\) obvykle volíme ve směru pohybujícího se tělesa. Pohyb ve směru osy \(y\) tedy nenastává, a matematický popis úlohy je jednodušší.
Podívejme se na zjednodušenou situaci, kdy se sáňkař pohybuje v ledovém korytě bez tření (viz obrázek 15.12). Předpokládejme, že dráha má tvar nakloněné roviny se sklonem \(\alpha=18^\circ\) vůči vodorovnému směru. Sáňkař i se saněmi má hmotnost \(m=105\ \mathrm{kg}\). Předchozí jízdou a dobrým startem již získal rychlost 75 km/h. Jaký bude jeho pohyb na nakloněné rovině? Jak velkou tlakovou silou působí dráha na sáňkaře?

Zdroj
Nejprve si situaci zakresleme do schématu (obrázek 15.13). Jediné dvě síly, které na sáňkaře působí, zanedbáme-li tření a odpor vzduchu, jsou tíhová síla \(\Vec{F}_\mathrm{G}\) a kolmá tlaková síla \(\Vec{F}_\mathrm{N}\). Jejich složením vznikne výslednice \(\Vec{F}\), která má konstantní směr i velikost. Působí ve směru pohybu sáňkaře, a přispívá tudíž k tomu, že se jeho rychlost zvyšuje.
Abychom dokázali jeho pohyb dobře popsat, zakresleme si do obrázku soustavu kartézských souřadnic. Protože se sáňkař pohybuje pouze v jednom směru, bude výhodnější, když osa \(x\) bude rovnoběžná s nakloněnou rovinou a orientována ve směru pohybu. Osa \(y\) bude tedy kolmá k nakloněné rovině. Její směr zvolme vzhůru (viz obrázek 15.13).

Zdroj
Druhý Newtonův zákon můžeme zapsat pomocí rovnice \(\Vec{F}_\mathrm{G}+\Vec{F}_\mathrm{N}=m\Vec{a}\). Tuto vektorovou rovnici následně rozepíšeme z pohledu obou souřadnicových os. Hledejme průměty působících sil a vektorů do směrů os \(x\) a \(y\). Kolmá tlaková síla \(\Vec{F}_\mathrm{N}\) směřuje v kladném směru osy \(y\) a promítne se tedy pouze do kladného směru této osy. Síla tíhová \(\Vec{F}_\mathrm{G}\) bude mít dvě složky: \(F_{\mathrm{G}x}\) směřující ve směru pohybu a určující zrychlení sáňkaře, zatímco složka \(F_{\mathrm{G}y}\) bude směřovat v záporném směru osy \(y\) a vyruší se s kolmou tlakovou silou. V tomto směru žádný pohyb nenastává (drobné nerovnosti dráhy neuvažujeme), tudíž i zrychlení ve směru osy \(y\) je nulové. Přejdeme ke skalárním rovnicím ve směrech souřadnicových os:
\[ \begin{aligned} x\colon&& F_{\mathrm{G}x} + 0 &= ma_x\\ y\colon&& -F_{\mathrm{G}y} + F_\mathrm{N} &= m\cdot0\\ \end{aligned} \]Pro velikost složek tíhové síly můžeme dále z pravoúhlého trojúhelníku ABC vyjádřit
\[ \sin\alpha=\frac{F_{\mathrm{G}x}}{F_\mathrm{G}} \quad\hbox{a}\quad \cos\alpha=\frac{F_{\mathrm{G}y}}{F_\mathrm{G}}\;, \]odkud pak vyjádříme velikosti jednotlivých složek:
\[ \begin{aligned} F_{\mathrm{G}x}&=F_\mathrm{G}\sin\alpha=mg\sin\alpha\\ F_{\mathrm{G}y}&=F_\mathrm{G}\cos\alpha=mg\cos\alpha\\ \end{aligned} \]Vektor zrychlení má pouze složku x-ovou, protože se závodník pohybuje pouze ve směru nakloněné roviny, osy \(x\). Zrychlení vyjádříme ve tvaru \(\Vec{a}=(a_x,a_y)=(g\sin\alpha,0)\). Pohyb sáňkaře po nakloněné rovině bez tření je tedy rovnoměrně zrychlený a velikost zrychlení závisí na sklonu nakloněné roviny vztahem \(a=a_x=g\sin\alpha\).
Pro velikost kolmé tlakové síly pak platí \(F_\mathrm{N}=F_{\mathrm{G}y}=mg\cos\alpha\). Po dosazení tedy vidíme, že velikost zrychlení sáňkaře je \(a=3{,}0\ \mathrm{m/s}^2\) a velikost kolmé tlakové síly \(F_\mathrm{N}=980\ \mathrm{N}\).
Chcete-li v úloze dále pokračovat, zjistěte, jakou bude mít závodník rychlost na konci této 40 m dlouhé nakloněné roviny. Jak to zjistíme?
Jestliže je pohyb sáňkaře přímočarý a rovnoměrné zrychlený, pro jeho rychlost platí
\[ v=at+v_0=g\sin\alpha+v_0\;. \]Vzdálenost \(d\) uražená sáňkařem na nakloněné rovině při rovnoměrně zrychleném pohybu je vyjádřena vztahem
\[ d = \frac12at^2+v_0t=\frac12g\sin\alpha\cdot t^2+v_0t\;, \]kde \(v_0\) je rychlost sáňkaře na počátku nakloněné roviny v čase \(t=0\ \mathrm{s}\).
Nejprve z druhé rovnice vypočítáme dobu jeho pohybu na dráze \(d=40\ \mathrm{m}\).
\[ \frac12g\sin\alpha\cdot t^2+v_0t-d=0\;. \]Po dosazení:
\[ \begin{aligned} \frac12\cdot9{,}8\cdot\sin(18^\circ)\cdot t^2+20{,}8t-40 &= 0\\ 1{,}51\cdot t^2+20{,}8t-40 &= 0\\ \end{aligned} \]Řešení této kvadratické rovnice jsou dvě: \(t=-15{,}4\ \mathrm{s}\) a \(t=1{,}71\ \mathrm{s}\). Zajímat nás bude jenom kladné řešení, čas pro nás začal plynout v okamžiku, kdy sáňkař vjel na nakloněnou rovinu. Jeho okamžitá rychlost po uplynutí tohoto času bude
\[ v(t=1{,}71\ \mathrm{s}) = 9{,}81\cdot\sin(18^\circ)\cdot1{,}71+20{,}8=26{,}0\ \mathrm{m/s}=93{,}6\ \mathrm{km/h} \]Zajímá vás, jak se bude sáňkař pohybovat v případě, že na něj bude působit odporová a třecí síla? Přečtěte si následující poznámku na okraj.
Chceme-li studovat reálný pohyb sáňkaře, musíme počítat se třením a odporovou silou. Metoda řešení je stejná. Použijeme druhý Newtonův zákon ve vektorové podobě a potom ho rozepíšeme do složek jednotlivých souřadných os.
Na závodníka \(m=105\ \mathrm{kg}\) bude působit tření mezi ledem a skluznicemi saní a také odporová síla vzduchu. Předpokládejme, že tyto síly jsou v naší úvaze konstantní a nezávislé na rychlosti sáňkaře. Řeknete si, že tomu tak ve skutečnosti není, a máte pravdu. Již ve 4. kapitole jsme ukázali, že odporová síla je úměrná druhé mocnině rychlosti. Takový výpočet je však značně komplikovaný, a proto si zavádíme tato zjednodušení. Podrobný výpočet, kdy na těleso působí proměnná síla, je uveden v laboratorní úloze této kapitoly.
Vezměme tedy například \(F_\mathrm{t}=50\ \mathrm{N}\) (\(f=0{,}05\)) a \(F_\mathrm{O}=15\ \mathrm{N}\). Ledové koryto je stále skloněno o 18° vůči vodorovnému směru a počáteční rychlost sáňkaře je 75 km/h. Jak se v tomto případě změní jeho rychlost na úseku o délce 40 m?
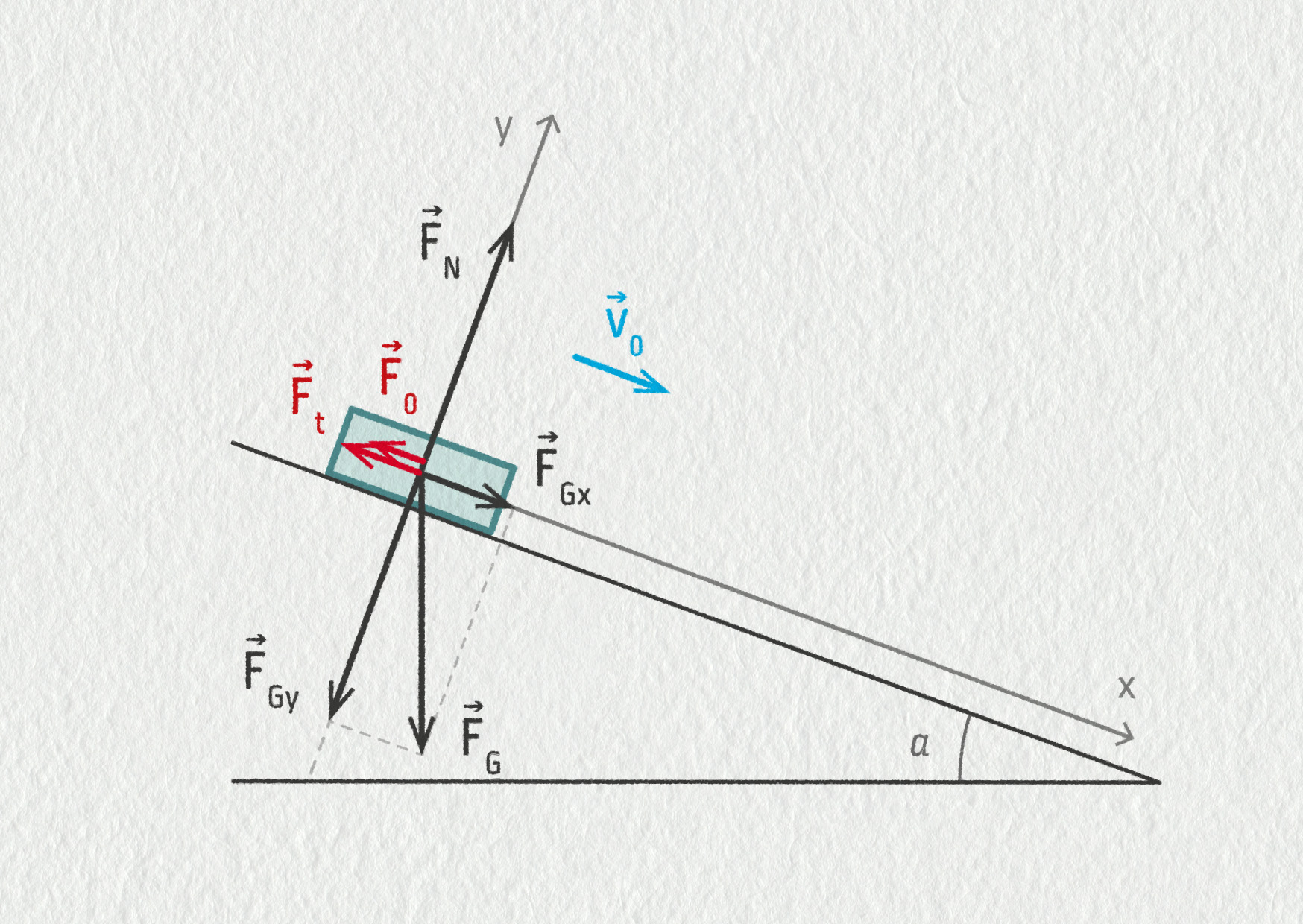
Zdroj
Druhý Newtonův zákon nám říká, že součet všech sil působících na těleso je roven součinu hmotnosti tělesa a jeho zrychlení:
\[ \sum_i \Vec{F}_i = m\Vec{a} \]V případě sáňkaře na nakloněné rovině máme tedy tyto průměty do os \(x\) a \(y\):
\[ \begin{aligned} x\colon&& F_{\mathrm{G}x} - F_\mathrm{t} - F_\mathrm{O} &= ma_x\\ y\colon&& -F_{\mathrm{G}y} + F_\mathrm{N} &= m\cdot0\\ \end{aligned} \]Odtud můžeme vyjádřit složky zrychlení sáňkaře
\[ \Vec{a} = \left(g(\sin\alpha-f\cos\alpha)-\frac{F_\mathrm{O}}m;0\right) = (2{,}42; 0)\ \mathrm{m}\cdot\mathrm{s}^{-2}\;. \]Opět se můžeme zabývat pouze pohybem ve směru osy \(x\). Rovnice pro rychlost sáňkaře má tvar
\[ v = at+v_0\;. \]Dráhu \(d\) vyjádříme podobně jako v předchozím případě
\[ d=\frac12\left[g(\sin\alpha-f\cos\alpha)-\frac{F_\mathrm{O}}m\right]t^2+v_0t \]Po číselném dosazení mají tyto rovnice tvar
\[ \begin{aligned} v&=2{,}42t+20{,}8\\ 40&=1{,}21t^2+20{,}8t\\ \end{aligned} \]Řešením druhé (kvadratické) rovnice \(1{,}21t^2+20{,}8t-40=0\) jsou časy \(t_1=-18{,}9\ \mathrm{s}\) a \(t_2=1,75\ \mathrm{s}\). Čas \(t_2\) odpovídá době pohybu sáňkaře na nakloněné rovině o délce 40 m. Proto tento čas dosadíme do první rovnice a vypočítáme rychlost sáňkaře po projetí této části ledového koryta:
\[ v=2{,}42\cdot1{,}75+20{,}8=25{,}0\ \mathrm{m/s}=90\ \mathrm{km/h}\;. \]Vidíme, že i když na závodníka působí dvě brzdné síly, jeho pohyb je stále zrychlený a rychlost narůstá poměrně rychle. Nakonec se ale vraťme k původním předpokladům o konstantní odporové síle. Ve skutečnosti bude narůstat s rostoucí rychlostí, až vyrovná průmět tíhové síly. Poté bude sáňkař pokračovat pohybem rovnoměrným a jeho rychlost již narůstat nebude.
Jaký je vlastně rozdíl mezi předchozími dvěma situacemi? Studovali jsme pohyb se třením a bez něj. Se třením na těleso působí více sil, výraz pro velikost zrychlení je komplikovanější, ale metoda řešení úlohy je stejná jako v případě „bez tření“: nejprve znázorníme všechny síly, které na těleso působí, podle druhého Newtonova zákona je sečteme, rozkladem sil ve směru souřadnicových os nalezneme složky vektoru zrychlení, a protože zde jde o pohyb v jednom směru, popisujeme ho pomocí jedné rovnice \(x=f(t)\).

