Kondenzátor
Cvičení 1
Deskový kondenzátor o kapacitě 47 µF byl připojen ke stejnosměrnému zdroji 6,0 V. Určete náboj na deskách a elektrickou energii uloženou v tomto deskovém kondenzátoru.
- \(Q=0{,}28\ \mathrm{mC}\);
- \(\mathcal{E}_\mathrm{C}=0{,}85\ \mathrm{mJ}\)
Cvičení 2
Vezmeme dvě kovové destičky o rozměrech 5 cm × 10 cm. Mezi ně vložíme papír o tloušťce 0,10 mm a pevně přitiskneme. Destičky nabijeme napětím 24 V.
- Vypočtěte permitivitu papíru podle vztahu \(\varepsilon=\varepsilon_\mathrm{r}\varepsilon_0\), kde \(\varepsilon_0\) je permitivita vakua a \(\varepsilon_\mathrm{r}\) je relativní permitivita papíru.
- Jakou kapacitu má tento kondenzátor?
- Jakou energii má tento kondenzátor?
- Jaká je intenzita elektrického pole mezi deskami kondenzátoru?
- 3,10 ⋅ 10−11 F/m (pro relativní permitivitu 3,50);
- 1,55 nF;
- 4,46 ⋅ 10−7 J;
- 240 kV/m
Cvičení 3
Kondenzátor o kapacitě 1 000 µF nabijeme napětím 48 V. Poté kondenzátor připojíme k rezistoru o odporu 10 Ω. Kondenzátor se začne vybíjet.
- Ve který okamžik teče rezistorem největší proud? Jakou má tento proud velikost?
- Jaké celkové teplo vznikne v rezistoru průchodem proudu při vybití kondenzátoru?
- Napětí na kondenzátoru je v každý okamžik rovno napětí na rezistoru. Největší proud teče ihned po připojení rezistoru, \(I_\mathrm{max}=U/R=4{,}8\ \mathrm{A}\), velikost proudu exponenciálně klesá k nule;
- 1,15 J
Cvičení 4
Nabíjení kondenzátoru je mnohem rychlejší než nabíjení elektrochemického akumulátoru. Proč tedy nevyužít kondenzátory k pohonu elektromobilů?
- Spočítejte, jakou celkovou kapacitu by musely mít kondenzátory, abychom v nich při napětí 400 V dokázali uložit energii 80 kWh, srovnatelnou s energií nabitého akumulátoru elektromobilu.
- Aby ve vzduchu nedošlo k výboji mezi deskami uvažovaného kondenzátoru, nesmí intenzita pole překročit 5 kV/cm. V jaké minimální vzdálenosti by se mohly nacházet desky těchto kondenzátorů a jaká je by byla jejich celková plocha?
- 3,6 kF;
- \(d=0{,}8\ \mathrm{mm}\), \(S=3{,}3\cdot10^5\ \mathrm{km}^2\), tj. přibližně čtyřnásobek rozlohy ČR
Cvičení 5
Kondenzátor o kapacitě \(C_1=10\ \mathrm{nF}\) nabijeme zdrojem na napětí \(U_1=20\ \mathrm{V}\). Pak jej od zdroje odpojíme a připojíme k němu vybitý kondenzátor o kapacitě \(C_2=40\ \mathrm{nF}\) – viz obrázek 18.53.
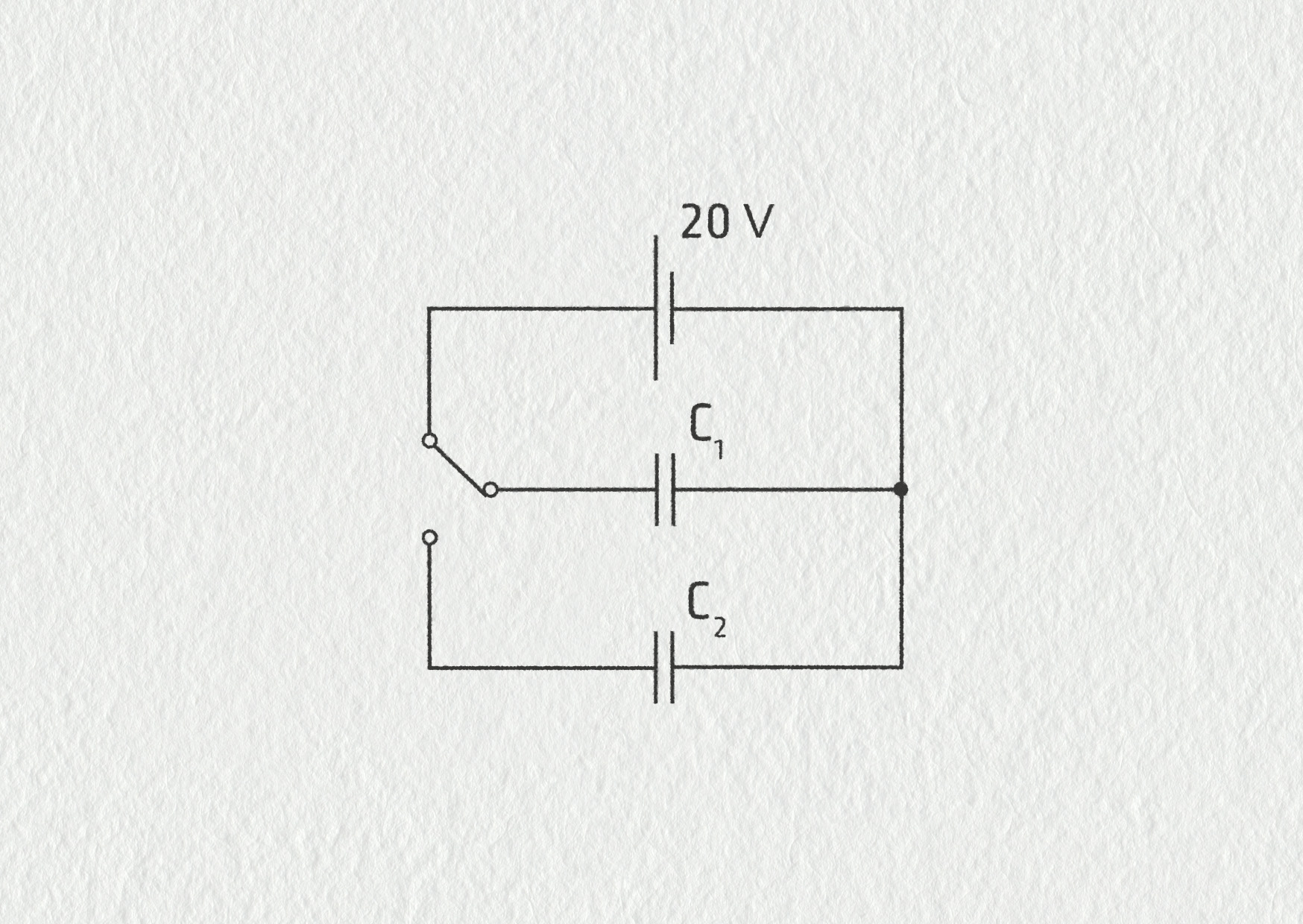
Zdroj
- Jaký náboj \(Q\) je na svorkách kondenzátoru \(C_1\) při napětí \(U_1\)?
- Po připojení druhého kondenzátoru se tento náboj \(Q\) rozdělí na oba kondenzátory. Jaké vznikne napětí mezi jejich svorkami?
- Jaký náboj \(Q_1\) a \(Q_2\) bude pak na jednotlivých kondenzátorech?
- 200 nC;
- 4 V;
- \(Q_1=40\ \mathrm{nC}\), \(Q_2=160\ \mathrm{nC}\)
Cvičení 6
Spojování kondenzátorů. Máme k dispozici dva kondenzátory o kapacitě \(C_1\) a \(C_2\).
- Dokažte obecně, že výsledná kapacita \(C\) kondenzátorů zapojených paralelně je \(C=C_1+C_2\).
- Dokažte obecně, že pro výslednou kapacitu \(C\) kondenzátorů zapojených sériově platí \(1/C=1/C_1+1/C_2\).
- Vypočítejte výslednou kapacitu kondenzátorů na obrázku.
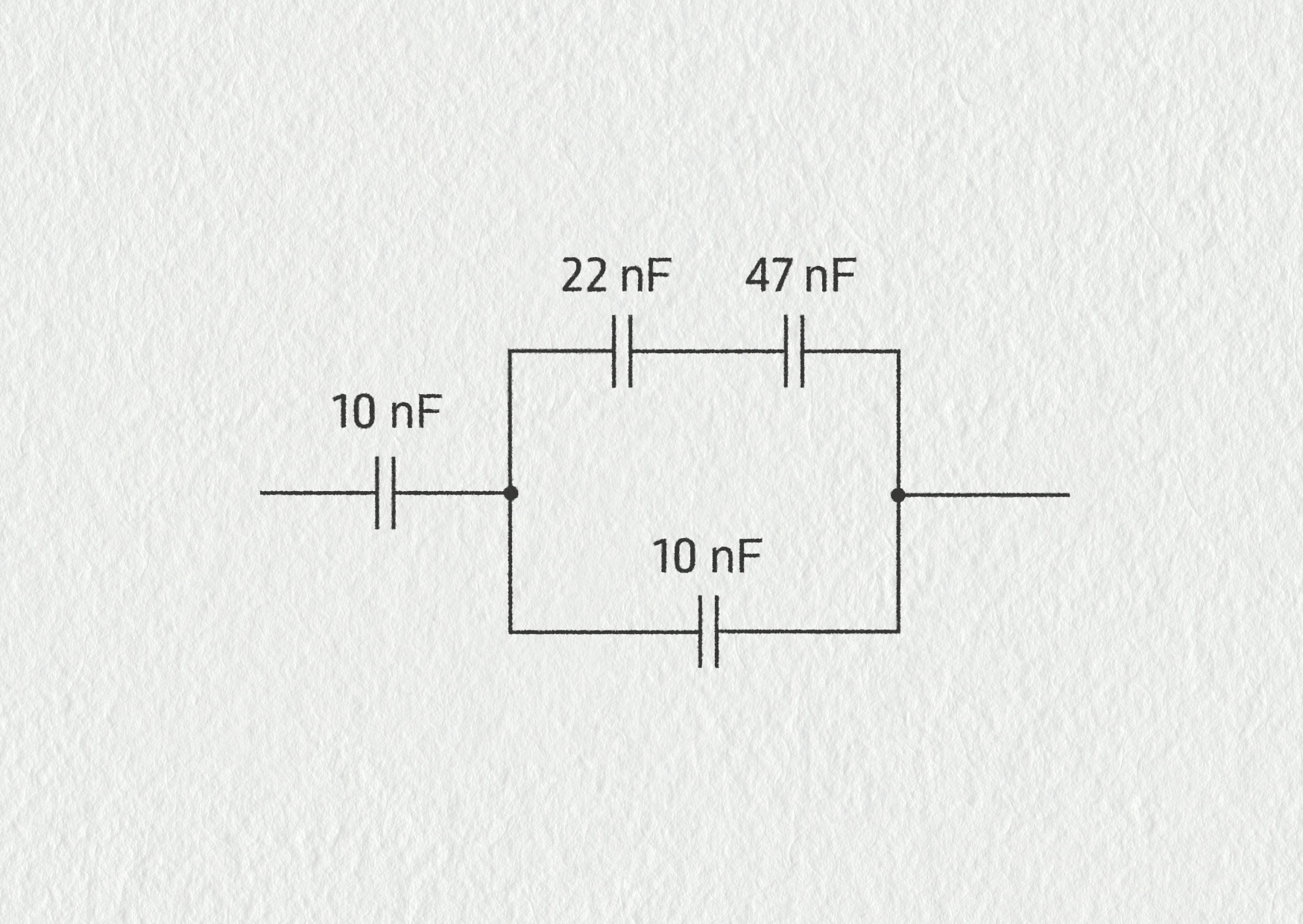
18.54 – Kondenzátor, cvičení 6
Zdroj - Jak musí být zapojeny tři kondenzátory o kapacitě 10 nF, aby jejich výsledná kapacita byla 15 nF? Nakreslete schéma.

