Urychlování částic
Cvičení 1
Jakou kinetickou energii má iont \(\mathrm{Ar}^+\), který byl urychlen napětím 200 V? Výsledek vyjádřete v základních jednotkách.
3,20 ⋅ 10−17 J
Cvičení 2
Jakým napětím byl urychlen proton, který získal rychlost 5,00 ⋅ 105 m/s? Hmotnost protonu je 1,67 ⋅ 10−27 kg.
1,30 kV
Cvičení 3
Olovnatý iont \(\mathrm{Pb}^{2+}\) byl urychlen napětím 1,5 kV. Vypočítejte hmotnost tohoto iontu a rychlost, kterou v urychlovači získal. Relativní atomová hmotnost olova je 207.
- 3,44 ⋅ 10−25 kg;
- 5,29 ⋅ 104 m/s
Cvičení 4
Jakou rychlost má proton o kinetické energii 2,00 GeV? Jaká je jeho hmotnost?
- \(v=0{,}978c\);
- \(m_0=3{,}56\cdot10^{-27}\ \mathrm{kg}\)
Cvičení 5
Na dvě svislé kovové desky A a B vzdálené 10 cm od sebe přivedeme napětí \(U_{AB}=+20\ \mathrm{kV}\). Malým otvorem v desce A vnikne do tohoto kondenzátoru proton o hmotnosti \(m_\mathrm{P}=1{,}67\cdot10^{-27}\ \mathrm{kg}\) s téměř zanedbatelnou rychlostí. Proton se pohybuje ve vakuu, tíhovou sílu neuvažujte.
- Nakreslete schéma uspořádání. Znázorněte polaritu desek, siločáry a intenzitu pole \(\Vec{E}\). Znázorněte elektrickou sílu působící na proton \(\Vec{F}_\mathrm{e}\), rychlost \(\Vec{v}\) a zrychlení protonu \(\Vec{a}\).
- Vypočítejte intenzitu pole, sílu a zrychlení protonu. Jaký pohyb vykonává?
- Vypočítejte, za jak dlouho proton proletí kondenzátorem, a rychlost, s níž dopadne na desku B.
- viz obrázek 18.34;
- \(E=200\ \mathrm{kV/m}\), \(F_\mathrm{e}=3{,}20\cdot10^{-14}\ \mathrm{N}\), \(a=1{,}92\cdot10^{13}\ \mathrm{m/s}^2\), pohyb přímočarý rovnoměrně zrychlený;
- \(t=1{,}02\cdot10^{-7}\ \mathrm{s}\), \(v_B=1{,}96\cdot10^6\ \mathrm{m/s}\)
Cvičení 6
Manipulace s elektronovým svazkem.
Vodorovné desky kondenzátoru mají délku \(l=2\ \mathrm{cm}\) a jejich vzdálenost je \(d=1\ \mathrm{cm}\). Přivedeme na ně napětí 114 V. V čase \(t=0\ \mathrm{s}\) vnikne do kondenzátoru urychlený elektron. Jeho rychlost v bodě O na ose kondenzátoru má vodorovný směr a velikost \(v_0=1{,}00\cdot10^7\ \mathrm{m/s}\). Elektron se pohybuje ve vakuu, tíhovou sílu zanedbáváme. Hmotnost elektronu je \(m_\mathrm{e}=9{,}11\cdot10^{-31}\ \mathrm{kg}\).
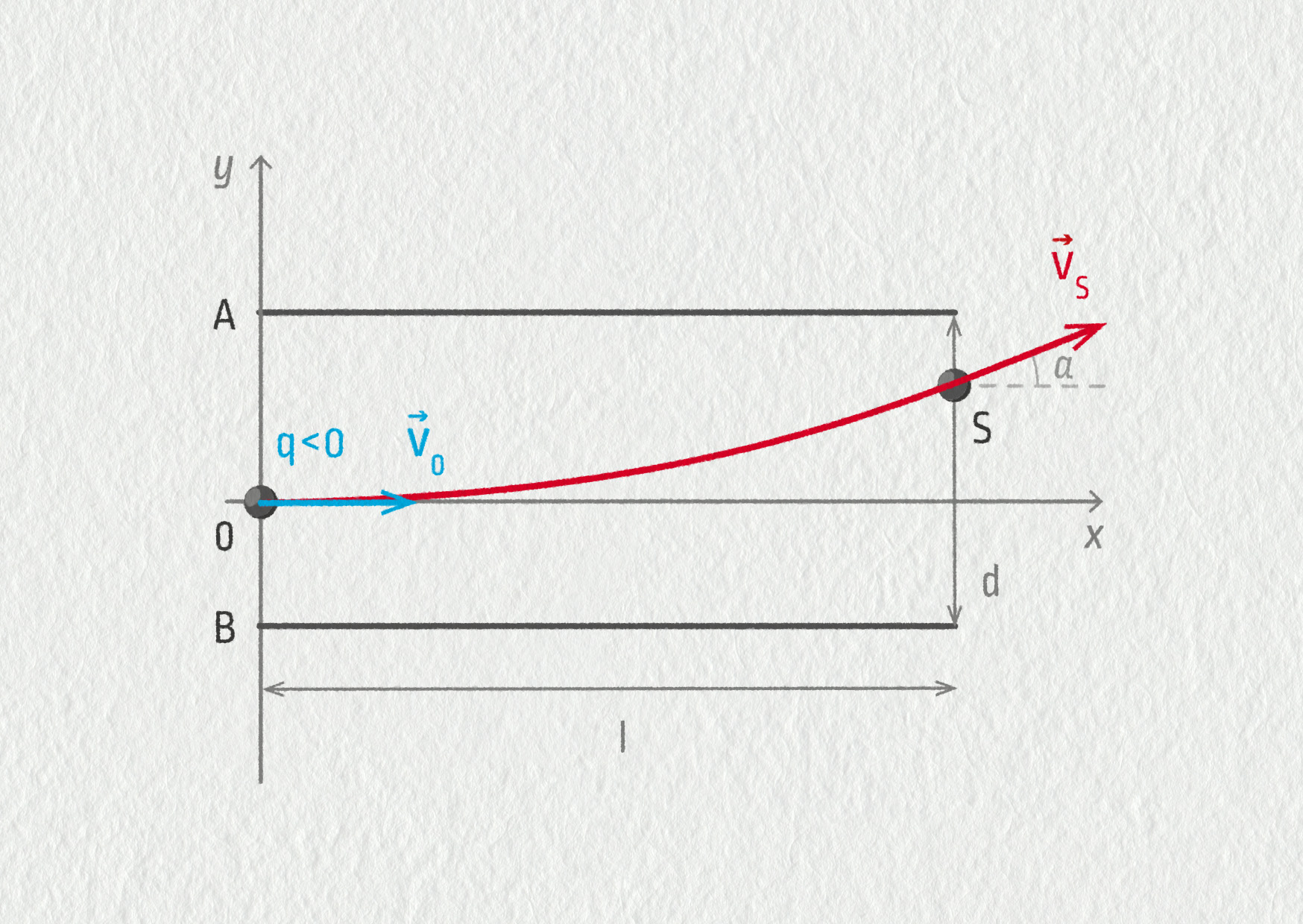
Zdroj
- Jaká je polarita desek, má-li být elektron urychlován směrem k desce A? Jaké znaménko má napětí \(U_{AB}\)?
- Do schématu zakreslete siločáry, intenzitu pole \(\Vec{E}\), elektrickou sílu působící na elektron \(\Vec{F}_\mathrm{e}\) a zrychlení elektronu \(\Vec{a}\).
- Vypočítejte velikost zrychlení elektronu.
- Odvoďte parametrické rovnice trajektorie elektronu \(x(t)\) a \(y(t)\).
- Odvoďte kartézskou rovnici trajektorie a určete, o jakou křivku se jedná.
- Určete souřadnice bodu S, kde elektron opouští kondenzátor.
- Vypočítejte velikost výstupní rychlosti \(v_S\) a úhel \(\alpha\), o který se směr pohybu elektronu odchýlil.
- deska A kladná, \(U_{AB}<0\);
- Vektory svislé, síla a zrychlení orientované nahoru, pole směrem dolů;
- 2 ⋅ 1015 m/s2;
- \(x=v_0t\), \(y=\frac12at^2\);
- \(y=ax^2/(2v_0^2)\), parabola. Pole bude dostatečně homogenní jen ve střední části, takže trajektorie jako celek parabolou nebude;
- \(x_S=l=2\ \mathrm{cm}\), \(\displaystyle y_S=\frac{qUx_S^2}{2mdv_0^2}=4{,}0\ \mathrm{mm}\);
- \(v_S=1{,}08\cdot10^7\ \mathrm{m/s}\), \(\alpha=21{,}8^\circ\)

