Každý elektrický spotřebič vyžaduje přesně daný druh napájení. Některé spotřebiče využívají bez úpravy střídavé napětí za zásuvky, jiné si je upravují podle potřeby. Podíváte-li se pozorně na napájecí zdroj k notebooku, uvidíte na něm podobné označení jako na obrázku níže. Jaké podstatné údaje je možné ze štítku zjistit?

Zdroj
To nejdůležitější lze shrnout následovně. Na vstup zdroje (PRI) je třeba připojit střídavé napětí 230 V, 50 Hz, což odpovídá síťové zásuvce. Na výstupu zdroje (SEC) bude stejnosměrné napětí 13 V. Hodnota 800 mA je pak maximální proud, který dokáže zdroj bezpečně dodávat do spotřebiče.
U všech zdrojů je nezbytné rozlišovat, zda generují stejnosměrné či střídavé napětí. Zdrojem stejnosměrného napětí jsou typicky galvanické články a baterie, zdrojem střídavého napětí je nejčastěji síťová zásuvka.
| Stejnosměrné napětí (proud) | DC (direct current) | = |
| Střídavé napětí (proud) | AC (alternating current) | ~ |
Důvodem, proč se v elektrické síti používá střídavé napětí a proud, je snadnější možnost změny napětí. Ztráty energie ve vodičích jsou totiž úměrné procházejícímu proudu. Při vyšším napětí můžeme stejný výkon přenášet pomocí menšího proudu (platí \(P=UI\)), výsledkem tedy budou i menší ztráty ve vodičích. Začněme ale pěkně od začátku a podívejme se na to, jak střídavé napětí měřit a jak ho jednoduše popsat.
Jak měříme střídavé napětí a proud?
Pro sledování elektrických signálů, které se v čase mění, používáme zařízení zvané osciloskop. Nemusí se jednat jen o střídavé napětí. Může jít třeba o elektrické signály v automobilu nebo o sledování elektrické aktivity srdce (EKG). Osciloskop měří hodnoty napětí a proudu s určitou vzorkovací frekvencí, která musí být přizpůsobená sledovanému signálu. Například vzorkovací frekvence 1 000 Hz znamená, že přístroj provede 1 000 měření za sekundu. Podobně fungují také měřící senzory, které připojujeme k počítači. Podrobněji se práci s osciloskopem věnujeme v praktickém cvičení.

Zdroj
Pojďme se nyní podívat na několik různých měření.
Zdroj
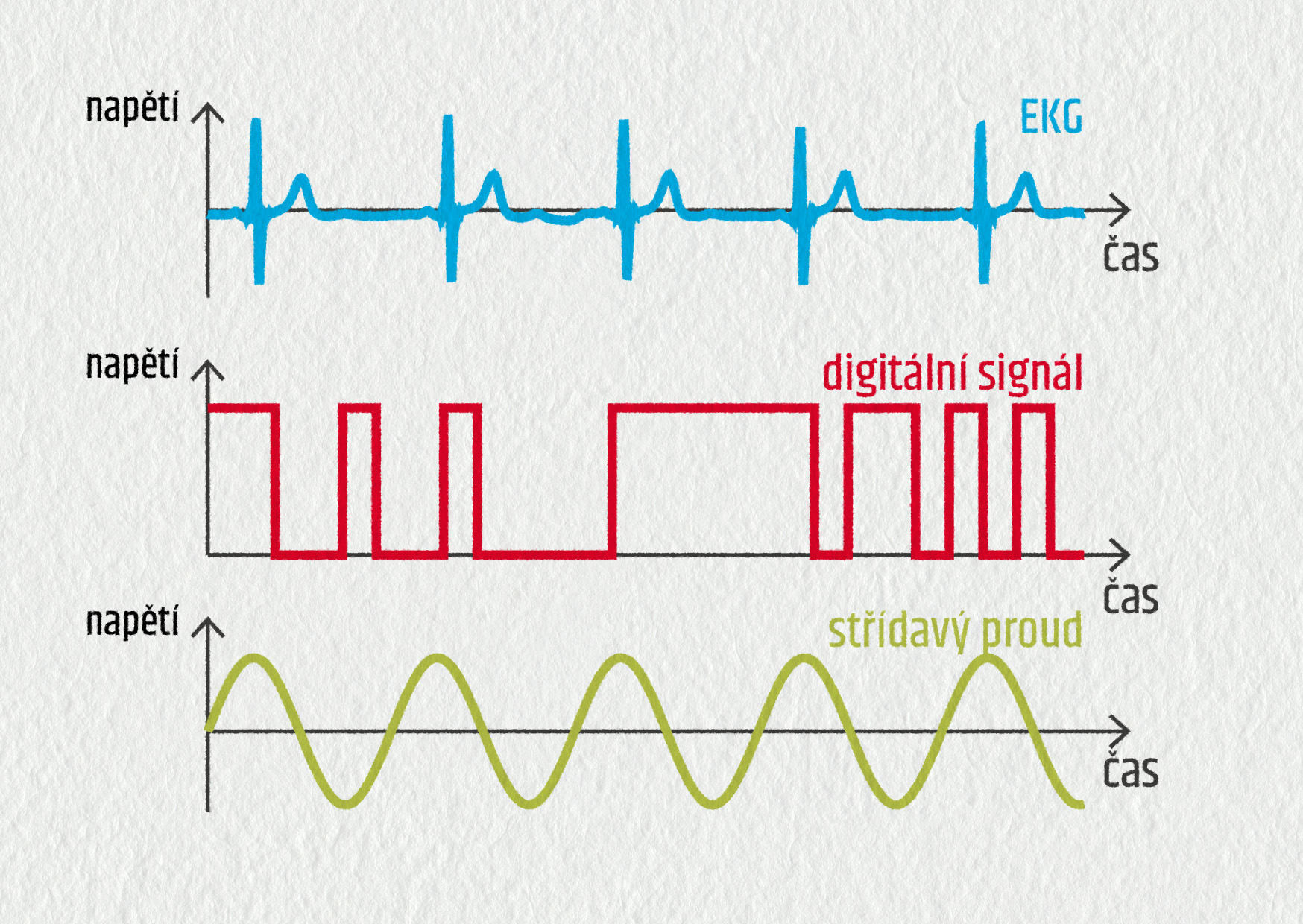
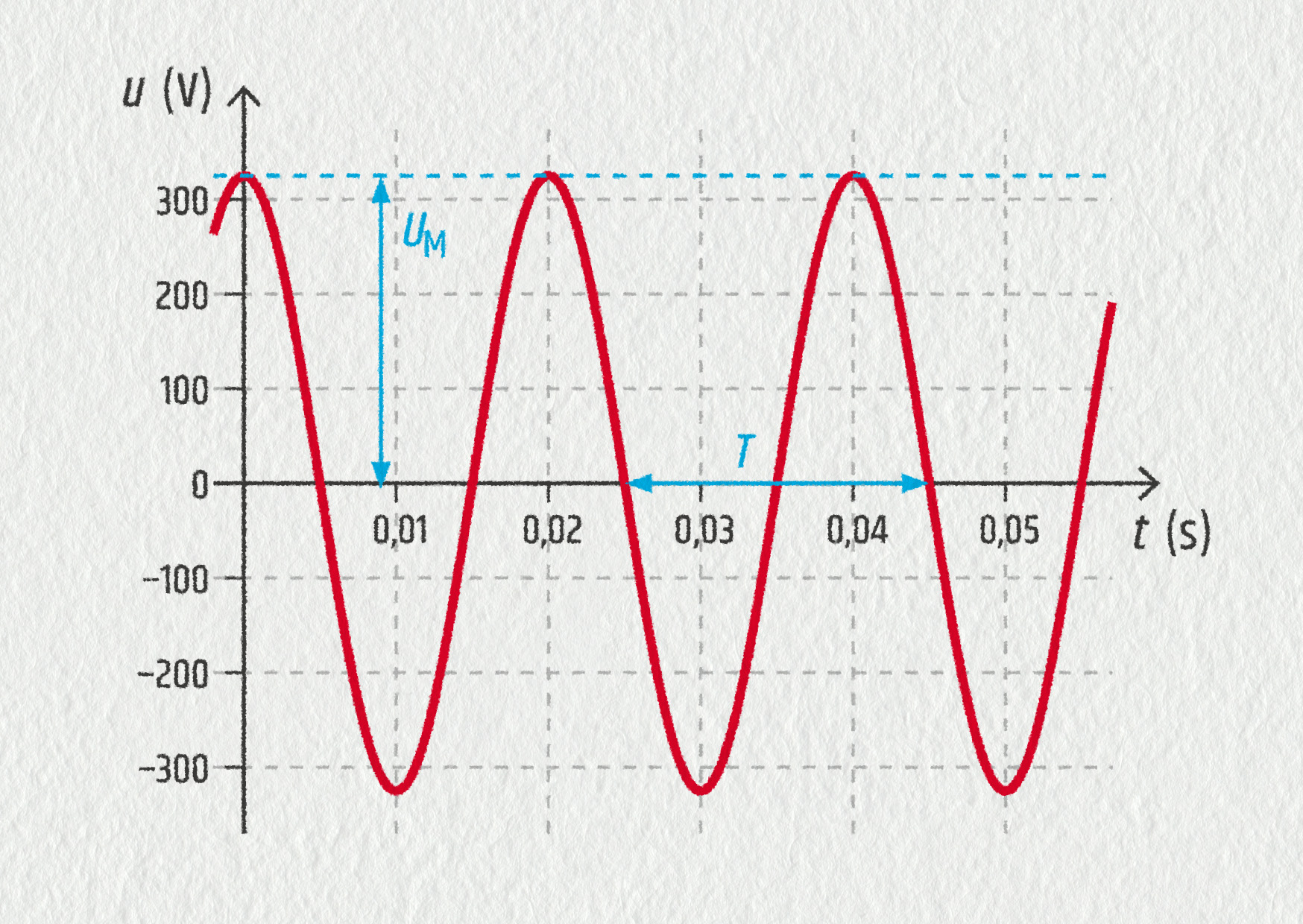
Na prvním obrázku vidíme časový průběh napětí ovládajícího srdeční sval – EKG. Vidíme, že signál se v čase opakuje, ale není přesně periodický. Jeho průběh nelze popsat jednoduchou matematickou funkcí. Druhý obrázek představuje zcela neperiodický signál – zprávu ve dvojkové soustavě. Takto spolu komunikují počítače (viz také kapitola 9). Na třetím obrázku vidíme střídavý proud sinusového průběhu. Tento signál je periodický a dokážeme jej matematicky poměrně jednoduše popsat. Co všechno můžeme z tohoto grafu zjistit? Graf jsme si pro tento účel zvětšili a vyznačili do něj důležité hodnoty.
Zdroj
Amplituda je maximální hodnota napětí, značíme ji \(U_\mathrm{M}\). Perioda je nejmenší čas, za který se průběh signálu začne opakovat, značíme ji \(T\). Kromě periody se používá ještě frekvence, což je převrácená hodnota periody – platí \(f=1/T\).
S těmito veličinami se setkáte všude tam, kde narazíte na periodické děje (například u mechanického kmitání v kapitole 21) Z našeho grafu pro střídavé napětí odečteme následující hodnoty: amplituda \(U_\mathrm{M}=325\ \mathrm{V}\); perioda \(T=0{,}02\ \mathrm{s}\). Výpočtem pak zjistíme také frekvenci \(f=1/T=50\ \mathrm{Hz}\).
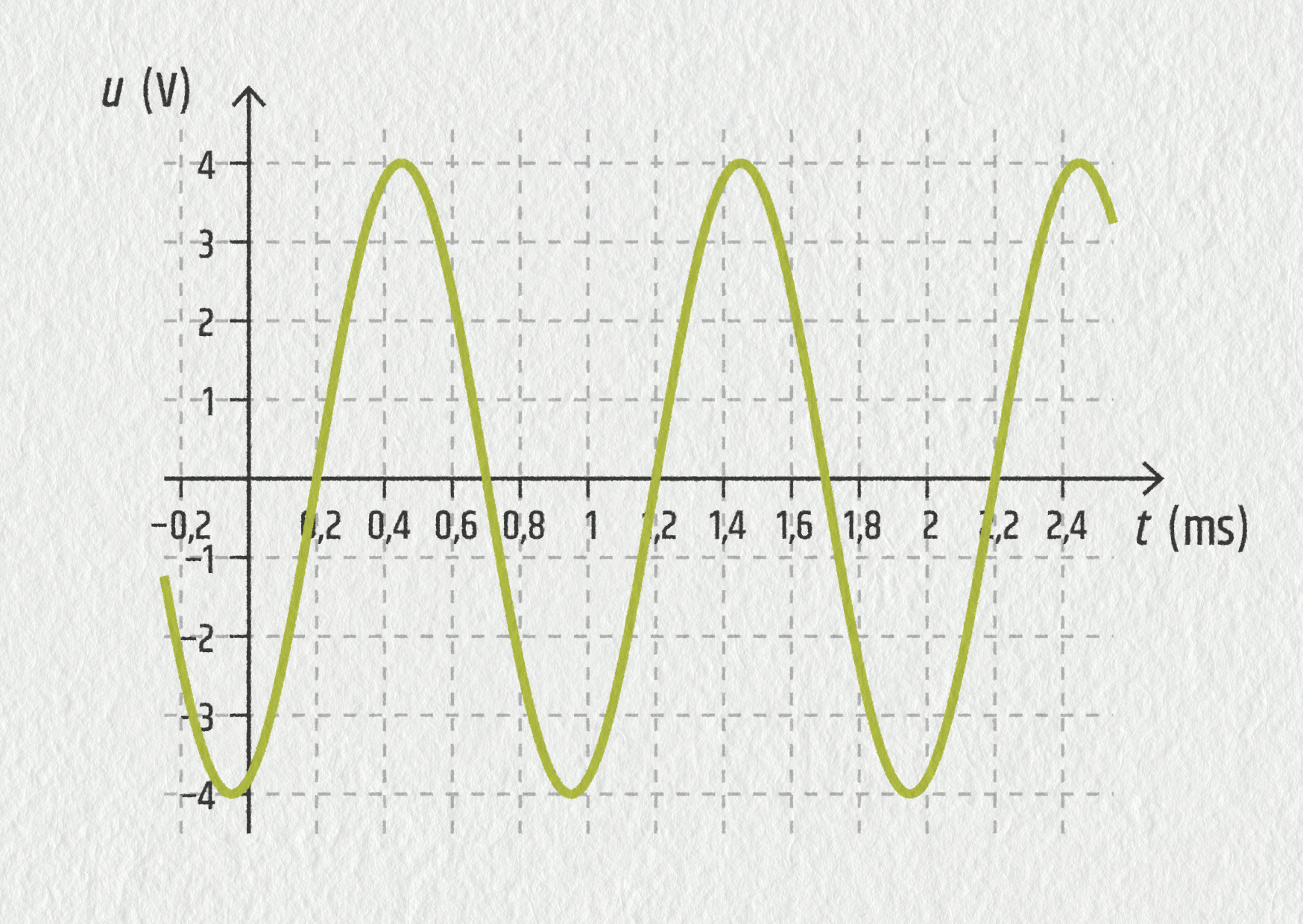
Určete amplitudu, periodu a frekvenci střídavého napětí z grafu (pozor – čas je v milisekundách).
Zdroj
Pokud jsou proud a napětí v čase neměnné, používáme pro ně velká písmena \(U\) a \(I\). V případě, že se napětí a proud v čase mění, používáme pro jejich okamžité hodnoty malá písmena \(u\) a \(i\). Funkce \(u(t)\) případně \(i(t)\) pak můžeme znázornit grafem, jak jsme viděli výše. V případě, že se jedná o sinusový průběh, není obtížné najít také předpis těchto funkcí. K tomu je dobré připomenout si význam parametrů obecné sinusové funkce v matematickém zápisu
\[ y(x) = A\sin(Bx+C)+D\;. \]Názorně to ukazuje tento applet: https://www.geogebra.org/m/zbgnkw4d.
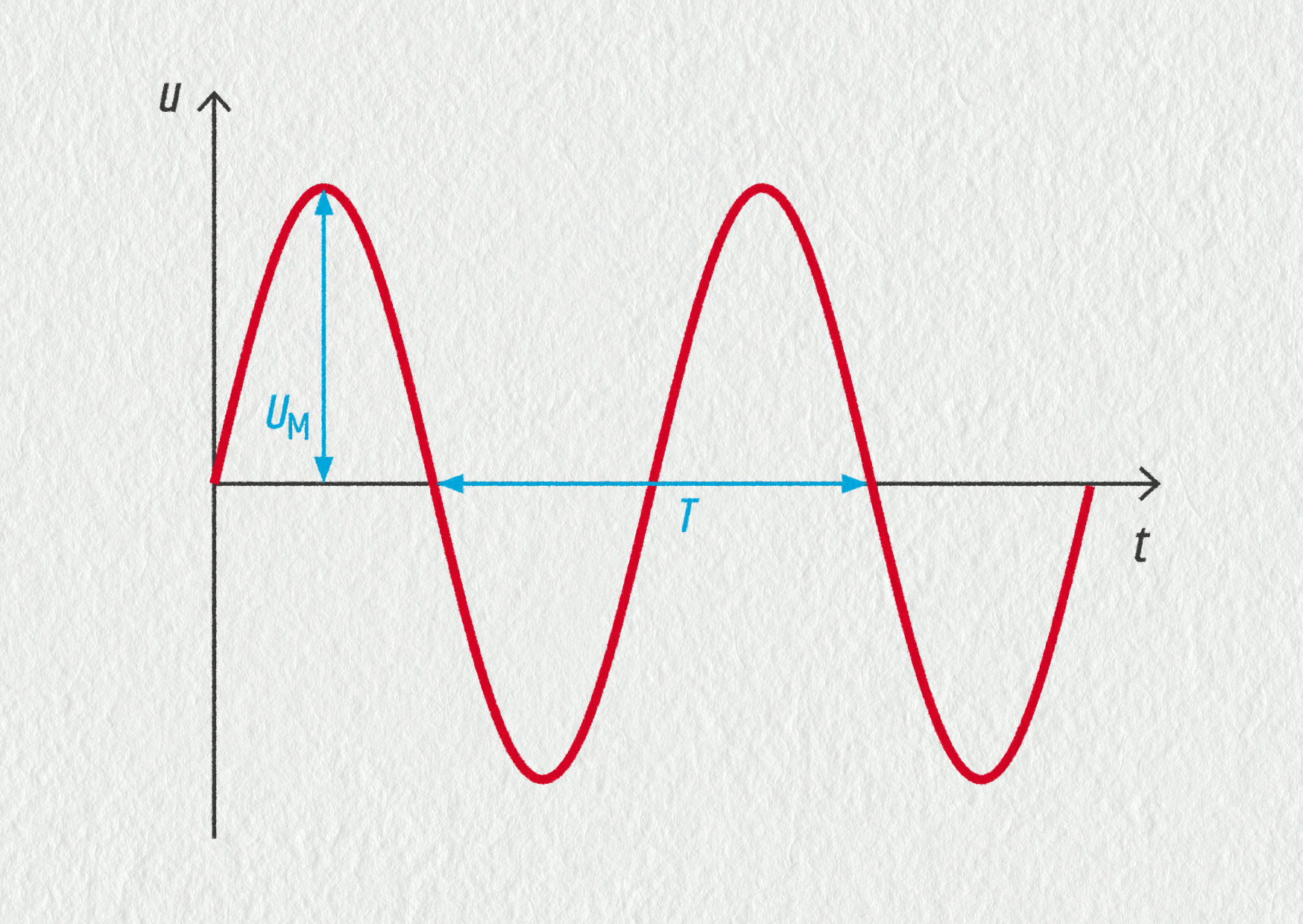
V případě sinusového napětí mají fyzikální význam zejména parametry \(A\), \(B\) a \(C\), které představují konkrétní fyzikální veličiny. Parametr \(A\) odpovídá amplitudě (maximální hodnotě) \(U_\mathrm{M}\). Parametr \(B\) se nazývá úhlová frekvence \(\omega\) s jednotkou rad ⋅ s−1. Platí
\[ \omega = \frac{2\pi}T = 2\pi f\;. \]Například je-li perioda \(T=4\ \mathrm{s}\), bude úhlová frekvence \(\omega=2\pi/4\ \mathrm{rad}\cdot\mathrm{s}^{-1} = \pi/2\ \mathrm{rad}\cdot\mathrm{s}^{-1}\). To znamená, že po uplynutí času \(t=1\ \mathrm{s}\) se napětí dostane do jedné čtvrtiny periody, což odpovídá úhlu \(\pi/2\ \mathrm{rad}\). Parametr \(C\) se pak označuje jako počáteční fáze \(\varphi_0\) a popisuje posun funkce na časové ose.
Nyní můžeme matematickou funkci y(x) přepsat do tvaru u(t) pomocí definovaných veličin:
\[ u(t) = U_\mathrm{M}\sin(\omega t + \varphi_0)\]Střídavé napětí
\[ u(t) = U_\mathrm{M}\sin(\omega t + \varphi_0) \]\(\omega=2\pi/T=2\pi f\) ... úhlová frekvence
\(U_\mathrm{M}\) ... amplituda (maximální hodnota)
\(T=1/f\) ... perioda (\(T\)) a frekvence (\(f\))
\(\varphi_0\) ... počáteční fáze
Zdroj
Zapište předpis funkce \(u(t)\) pro střídavé napětí sinusového průběhu s parametry: \(U_\mathrm{M}=325\ \mathrm{V}\), \(f=50\ \mathrm{Hz}\).
Stačí nám vypočítat úhlovou frekvenci \(\omega=2\pi f=314\ \mathrm{rad}\cdot\mathrm{s}^{-1}\) a dosadit do předpisu pro napětí. Do vztahu pro větší přehlednost zpravidla neuvádíme jednotky, píšeme jen číselné hodnoty veličin:
\[ u(t) = U_\mathrm{M}\sin(\omega t) = 325\sin(314t)\;. \]Poznámka: Počáteční fáze se většinou volí nulová. Její význam vynikne až v případě, kdy uvažujeme více různých funkcí.
Jednoduchý obvod s rezistorem
Jak se bude chovat elektrický obvod, který bude napájen střídavým napětím? Základní znalosti o elektrických obvodech již máme z kapitoly 8 a mnohé z nich zde použijeme. Pojďme si nakreslit schéma jednoduchého obvodu s žárovkou a zdrojem střídavého napětí.
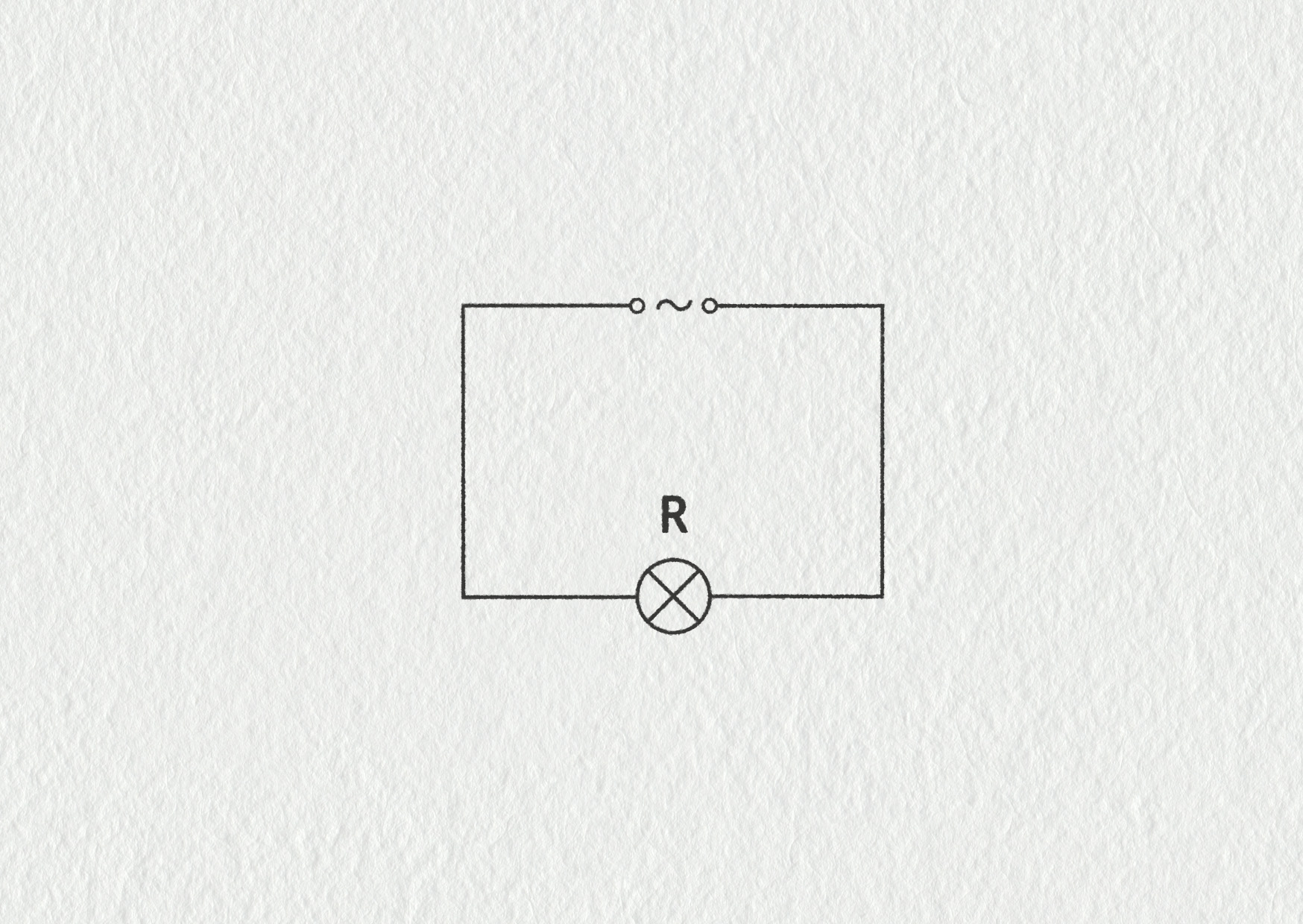
Zdroj
Žárovka se v obvodu projevuje svým odporem \(R\). Proud protékající žárovkou se v případě stejnosměrného zdroje vypočítá jako \(I=U/R\). Tento vztah platí i nyní, ovšem tentokrát pro okamžité hodnoty proudu a napětí. Elektrický proud bude svým průběhem „kopírovat“ průběh napětí. Pokud bychom měřili napětí a proud současně, dopadlo by to nějak takto:
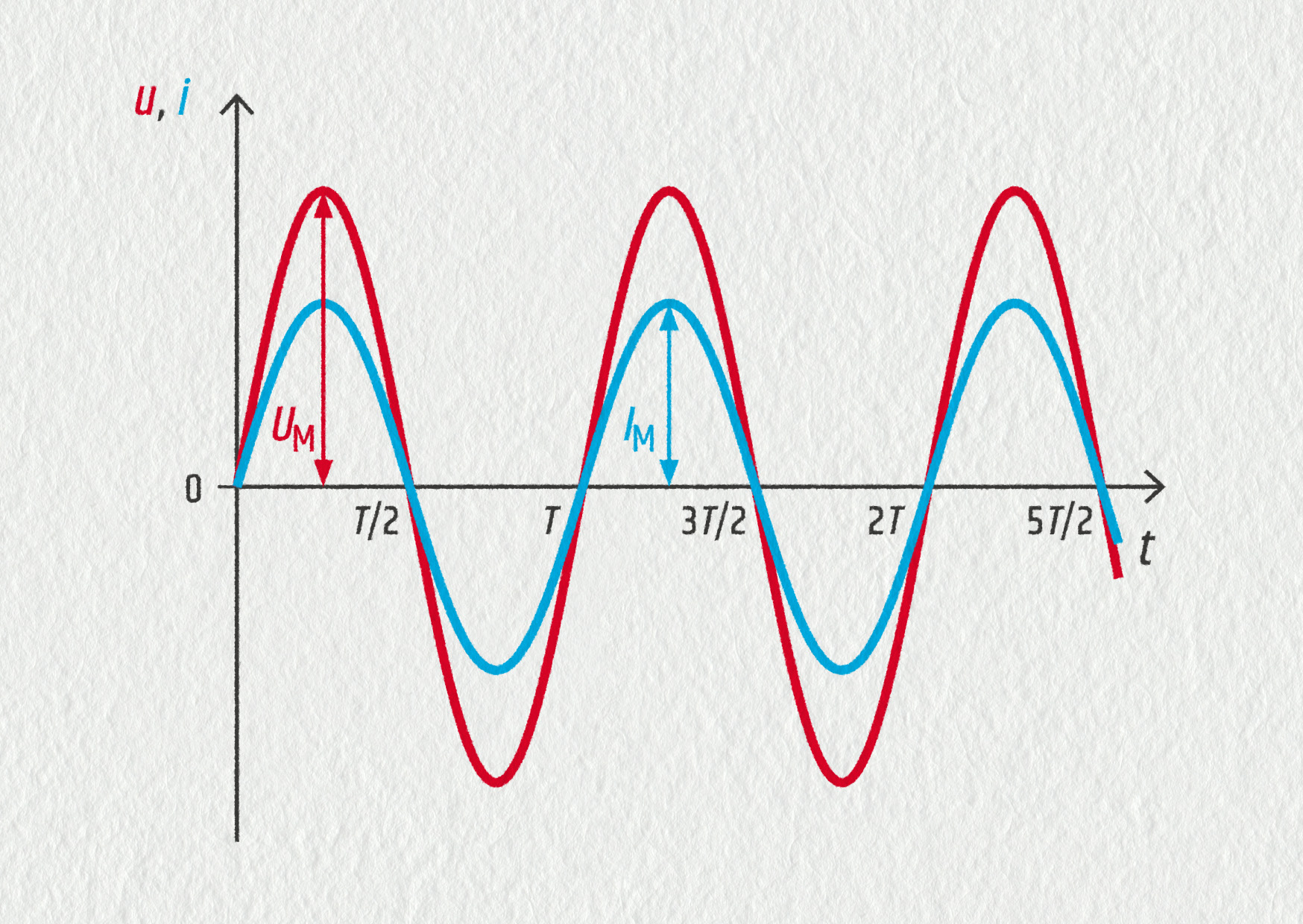
Zdroj
Matematicky to můžeme zapsat také docela jednoduše jako
\[ i=\frac uR=\frac{U_\mathrm{M}\sin(\omega t)}R=\frac{U_\mathrm{M}}R\sin(\omega t)=I_\mathrm{M}\sin(\omega t)\;, \]kde \(I_\mathrm{M}=U_\mathrm{M}/R\) je amplituda (maximální hodnota) proudu.
Mnohem zajímavější bude odpověď na otázku, jak je to s výkonem předaným spotřebiči. Je jasné, že výkon (a tedy i svit žárovky) bude v čase kolísat. Tyto změny jasu však nejsou při vyšších frekvencích než cca 50 Hz lidským okem rozpoznatelné (více v motivační aktivitě). Pro okamžitý výkon platí známý vztah \(p=ui\), kde \(u\) a \(i\) jsou nyní okamžité hodnoty napětí a proudu. Dosazením za \(i\) dostaneme
\[ p=ui=Ri^2= RI_\mathrm{M}^2\sin^2(\omega t)\;. \]Graf této funkce \(p(t)\) vypadá takto:
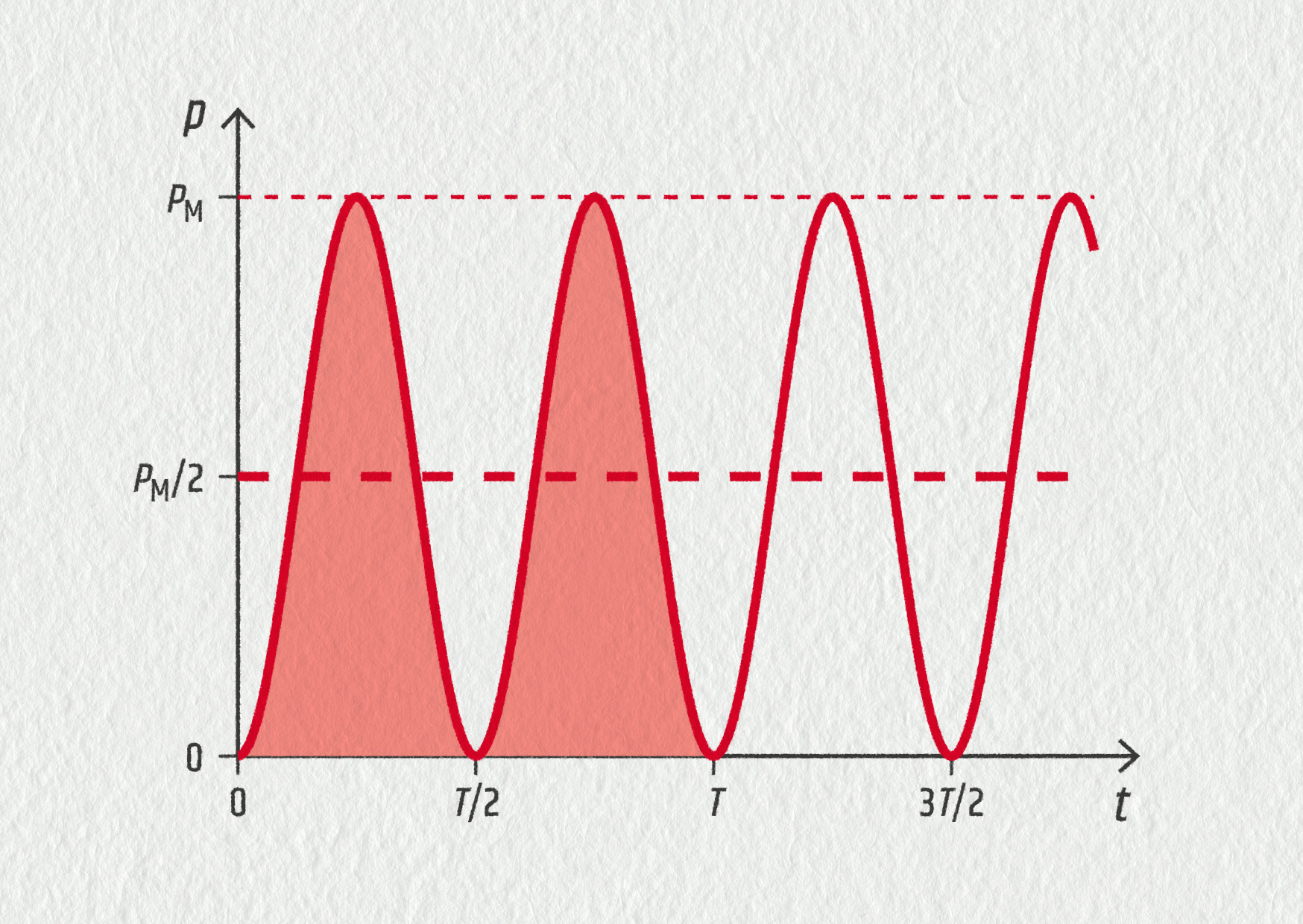
Zdroj
Vidíme, že výkon se pohybuje mezi nulou a maximem \(P_\mathrm{M}=U_\mathrm{M}I_\mathrm{M}\). V grafu je vyznačen také průměrný výkon \(P_\mathrm{P}=P_\mathrm{M}/2\). Žárovka tedy svítí v průměru přesně polovičním výkonem, než jaký by měla při stejnosměrném napětí o velikosti \(U_\mathrm{M}\) a proudu \(I_\mathrm{M}\). Z praktických důvodů byly zavedeny efektivní veličiny: efektivní napětí \(U_\mathrm{ef}\) a efektivní proud \(I_\mathrm{ef}\), pro které platí:
\(\displaystyle U_\mathrm{ef}=\frac{U_\mathrm{M}}{\sqrt2}\) a \(\displaystyle I_\mathrm{ef}=\frac{I_\mathrm{M}}{\sqrt2}\) – efektivní napětí a proud
\(\displaystyle P_\mathrm{P}=\frac12 U_\mathrm{M}I_\mathrm{M}=\frac{U_\mathrm{M}}{\sqrt2}\frac{I_\mathrm{M}}{\sqrt2}=U_\mathrm{ef}I_\mathrm{ef}\) – průměrný výkon střídavého proudu
Efektivní hodnoty jsou tedy definované tak, aby se dal průměrný výkon na rezistoru vypočítat jako jejich součin (to znamená stejně jako u stejnosměrného proudu). Pokud měříme střídavý proud a napětí multimetrem, přístroj ukazuje efektivní hodnoty. V případě síťové zásuvky multimetr ukáže efektivní hodnotu 230 V, zatímco maximální hodnota je \(U_\mathrm{M}=\sqrt2\cdot230\ \mathrm{V}=325\ \mathrm{V}\).
Při měření multimetrem v obvodu AC jsme na žárovce získali hodnoty 20 V a 0,25 A.
Vypočítejte průměrný a maximální výkon spotřebiče.
Průměrný výkon: \(P_\mathrm{P} = U_\mathrm{ef} I_\mathrm{ef} = 5\ \mathrm{W}\).
Maximální výkon: \(P_\mathrm{M} = 2P_\mathrm{P} = 10\ \mathrm{W}\).
Doplňte správné hodnoty napětí ve voltech pro síťovou zásuvku:
Obvod s rezistorem se při napájení střídavým zdrojem chová docela jednoduše, protože časový průběh proudu „kopíruje“ napětí. Odborně říkáme, že proud a napětí v obvodu s rezistorem nejsou fázově posunuté. Při zapojení cívky či kondenzátoru naopak dochází k fázovému posunutí proudu vůči napětí. Tím se situace komplikuje, neboť křivka okamžitého výkonu zasahuje i do záporných hodnot. Záporné hodnoty výkonu znamenají, že cívka a (nebo) kondenzátor se v danou chvíli chovají jako zdroje, dodávají do obvodu energii. Při nenulovém fázovém posunu je tedy průměrný výkon vždy menší než \(P_\mathrm{P}=\frac12P_\mathrm{M}\). Přehledně to ukazuje následující graf nebo tento applet: https://www.geogebra.org/m/p3cggxb3.
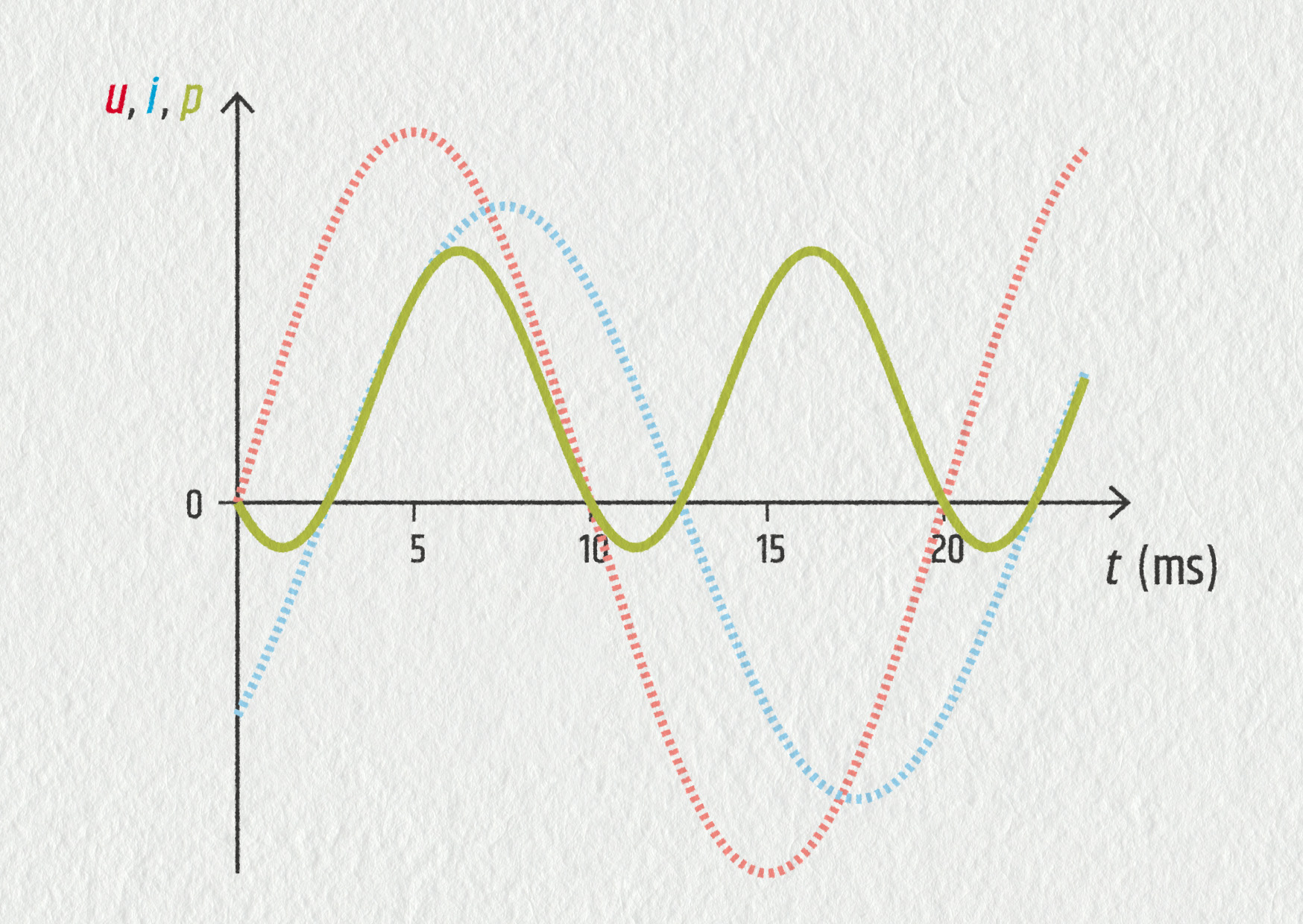
Zdroj
a) Obvod s cívkou
Zapojíme-li cívku ke zdroji střídavého napětí, bude se v jejím jádře vytvářet střídavé magnetické pole. Cívka se tak bude nacházet v proměnlivém magnetickém poli, které sama vytvořila, a bude v ní docházet k elektromagnetické indukci. Jev se nazývá vlastní indukce v cívce. Cívka se stává zdrojem napětí, které je posunuté vůči napětí zdroje a má opačné znaménko. V důsledku toho se proud zpožďuje za napětím. Proud protékající cívkou je nyní určen její indukčností \(L\) a úhlovou frekvencí \(\omega\). Veličina v ohmech, která má význam „odporu cívky“ pro střídavý proud, se nazývá induktivní reaktance \(X_L\) a platí pro ni
\[ X_L = \frac{U_\mathrm{M}}{I_\mathrm{M}} = \omega L\;. \]b) Obvod s kondenzátorem
Zapojíme-li kondenzátor ke zdroji střídavého napětí, bude se střídavě nabíjet a vybíjet. V obvodu poteče proud, který je maximální v okamžiku, kdy je kondenzátor vybitý. Naopak při plně nabitém kondenzátoru je proud nulový. Proud tedy předbíhá napětí. Proud protékající kondenzátorem je nyní určen jeho kapacitou \(C\) a úhlovou frekvencí \(\omega\). Veličina v ohmech, která má význam „odporu kondenzátoru“ pro střídavý proud, se nazývá kapacitní reaktance \(X_C\) a platí pro ni
\[ X_C = \frac{U_\mathrm{M}}{I_\mathrm{M}} = \frac1{\omega C}\;. \]Výše uvedené vztahy tvoří základ pro fyzikální popis obvodů střídavého proudu. Zde uveďme pro ilustraci alespoň jednouchý příklad. Cívka a kondenzátor mohou sloužit jako tzv. frekvenční filtry. Vysoké frekvence snadněji projdou kondenzátorem (\(X_C=1/(\omega C)\) je malé), zatímco nízké frekvence zase cívkou (\(X_L=\omega L\) je malé). Při použití cívky a kondenzátoru současně můžeme obvod „naladit“ na určitou frekvenci, která bude obvodem nejlépe procházet. Přesně tak se ladí rádio!

