Princip urychlování částic
Prozkoumáme vlastnosti pohybu nabité částice v homogenním elektrickém poli. Použijeme obecný postup, který už známe z mechaniky: na základě vlastností pole určíme působící sílu, z ní zrychlení a pak pomocí počátečních podmínek ostatní veličiny popisující pohyb.
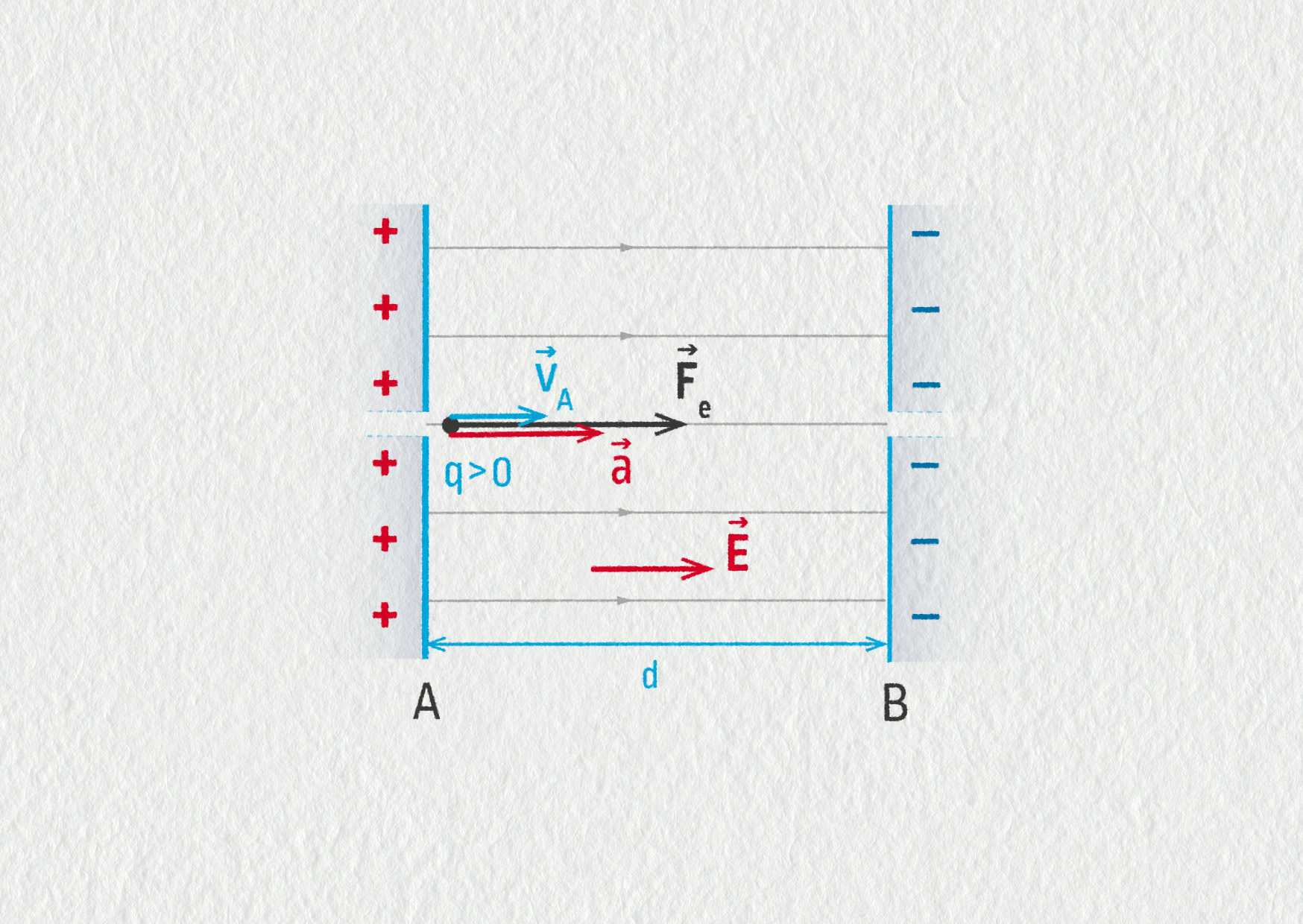
Částice s nábojem \(q>0\) a hmotností \(m\) vstoupí do homogenního elektrického pole rychlostí \(\Vec{v}_A\) malým otvorem v desce A. Předpokládáme, že počáteční rychlost \(\Vec{v}_A\) je rovnoběžná se směrem siločar. Budeme také předpokládat, že mezi deskami je vakuum. V opačném případě by částice neměla volnou dráhu a srážela by se s molekulami vzduchu.
Zdroj
V prostoru mezi nabitými deskami A a B existuje homogenní elektrické pole, jehož intenzitu určíme ze vztahu \(E=U_{AB}/d\), kde \(U_{AB}\) je napětí mezi deskami a \(d\) jejich vzdálenost. Na částici v tomto poli působí elektrická síla \(\Vec{F}_\mathrm{e}\), jejíž směr je rovnoběžný se siločárami a vektorem \(\Vec{E}\). Kladná částice je odpuzována kladnou deskou A a přitahována zápornou deskou B. Velikost elektrické síly vypočítáme z definice intenzity pole: \(\Vec{F}_\mathrm{e}=qE\).
Tíhovou sílu \(F_\mathrm{G}\) zanedbáme, v praxi nehraje žádnou roli, neboť je o mnoho řádů menší než \(\Vec{F}_\mathrm{e}\). Výslednice sil je tedy rovna elektrické síle \(\sum\Vec{F}=\Vec{F}_\mathrm{e}\).
Podle druhého Newtonova zákona je výslednice sil rovna součinu hmotnosti a zrychlení
\[ \sum\Vec{F} = m\Vec{a}\;. \]V našem případě tedy platí \(\Vec{F}_\mathrm{e}=m\Vec{a}\). Zrychlení částice je rovnoběžné s elektrickou silou, má směr siločar. Jeho velikost je
\[ a = \frac{F_\mathrm{e}}m = \frac{qE}m = \frac{qU}{md}\;. \]Zrychlení má tedy konstantní směr i velikost.
Počáteční rychlost \(\Vec{v}_A\) je rovnoběžná se zrychlením. Z vlastností zrychlení proto plyne, že pohyb částice musí být přímočarý rovnoměrně zrychlený. Pro tento typ pohybu můžeme používat známé vztahy pro rychlost a dráhu (viz kapitola 3):
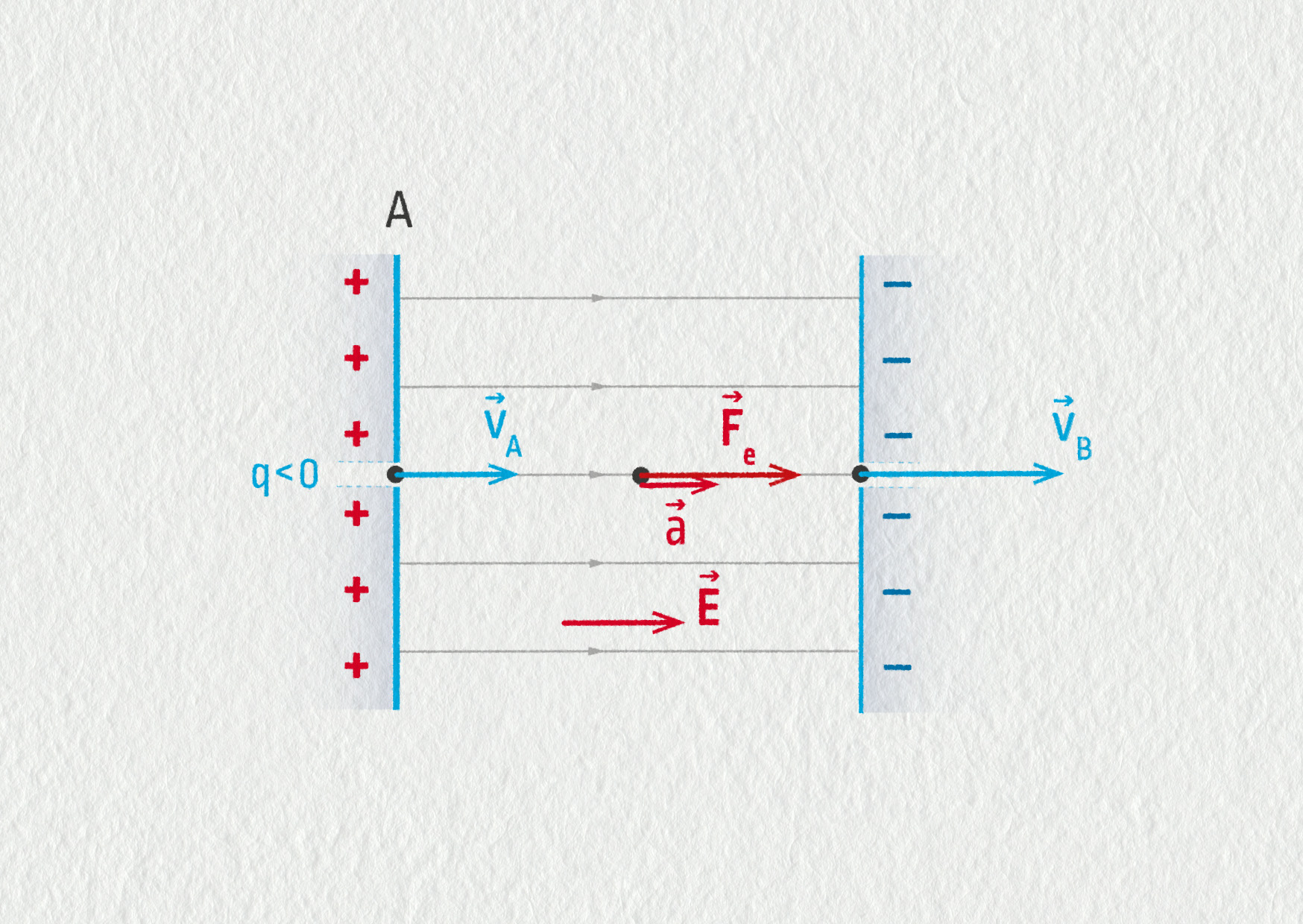
\[\begin{aligned} v&=at+v_A\\ s&=\frac12at^2+v_At\\ \end{aligned}\]Elektron vletí do homogenního elektrického pole rychlostí 105 m/s malým otvorem v desce A. Směr počáteční rychlosti je rovnoběžný se siločárami. Pole je vytvořeno mezi deskami A a B nabitými napětím 200 V a vzdálenými 10 cm. V prostoru mezi deskami je vakuum. Hmotnost elektronu je 9,1 ⋅ 10−31 kg, jeho náboj znáte zpaměti. Určete
- polaritu desek, aby byl elektron urychlován,
- elektrickou a tíhovou sílu působící na elektron,
- zrychlení elektronu,
- výstupní rychlost, jakou elektron proletí malým otvorem v desce B.
Zdroj
a) Elektron je záporný, \(q_\mathrm{e}=-1{,}6\cdot10^{-19}\ \mathrm{C}\). Deska A jej musí odpuzovat a deska B přitahovat, tedy deska A je nabita záporně, deska B kladně.
b)
\[ F_\mathrm{e} = |q_\mathrm{e}|E = |q_\mathrm{e}|\frac Ud = 1{,}6\cdot10^{-19}\cdot\frac{200}{0{,}1}\ \mathrm{N} = 3{,}2\cdot10^{-16}\ \mathrm{N}\;, \]směr rovnoběžný se siločárami, orientace opačná.
\[ F_\mathrm{G} = mg = 9{,}1\cdot10^{-31}\cdot9{,}8\ \mathrm{N}=8{,}9\cdot10^{-30}\ \mathrm{N}\;. \]Tíhová síla je o 13 řádů menší než elektrická, můžeme ji zanedbat.
c)
\[ a = \frac{F_\mathrm{e}}m = 3{,}5\cdot10^{14}\ \mathrm{m/s}^2\;, \]směr a orientace shodná s elektrickou silou.
d) Elektron koná pohyb přímočarý rovnoměrně zrychlený. Ke zjištění výstupní rychlosti \(v_B\) ze vzorce \(v_B=at+v_A\) potřebujeme nejdříve spočítat dobu \(t\) průchodu mezi deskami. K tomu použijeme vztah pro dráhu
\[ d = \frac12at^2+v_A \]vedoucí na kvadratickou rovnici pro \(t\), kterou musíme vyřešit:
\[ 0{,}10 = \frac12\cdot3{,}5\cdot10^{14}\cdot t^2+10^5\cdot t \]Kladné řešení rovnice je \(t=2{,}36\cdot10^{-8}\ \mathrm{s}\).
Dosazením do vztahu pro rychlost získáváme \(v_B=8{,}4\cdot10^6\ \mathrm{m/s}\).
Že se vám nechtělo řešit kvadratickou rovnici a podívali jste se až na výsledek? Máte pravdu, tento přímý postup sice funguje vždy, je ale poněkud těžkopádný. Výstupní rychlost \( v_B \) můžeme totiž získat mnohem elegantněji pomocí energií – čtěte dál.
Elektronvolt
Kinetická neboli pohybová energie je definována pomocí práce, kterou je třeba vykonat k urychlení tělesa z klidu na danou rychlost. V elektrickém poli nabitou částici urychluje elektrická síla \(\Vec{F}_\mathrm{e}\). Její práci počítáme ze vztahu
\[W_\mathrm{e}=qU,\]kde \(q\) je náboj částice a \(U\) napětí mezi místy, kterými částice prošla (nejčastěji napětí mezi nabitými urychlujícími deskami). Elektron nebo proton, který je urychlen napětím 1 V, získá kinetickou energii
\[ \mathcal{E}_\mathrm{C} = W_\mathrm{e} = qU =\] \[= 1{,}602\cdot10^{-19}\ \mathrm{C}\cdot1\ \mathrm{V}=1{,}602\cdot10^{-19}\ \mathrm{J} \]Definice elektronvoltu
Elektronvolt je energie, kterou získá elektron urychlený napětím jeden volt.
1 eV = 1,602 ⋅ 10—19 J
V jaderné a částicové fyzice se používají násobky elektronvoltu: keV, MeV, GeV = 109 eV, TeV = 1012 eV.
Vyřešíme ještě jednou předchozí úlohu. Elektron vletí do homogenního elektrického pole rychlostí 105 m/s malým otvorem v desce A . Směr počáteční rychlosti je rovnoběžný se siločárami. Pole je vytvořeno mezi deskami A a B mezi kterými je napětí 200 V a vzdálenými 10 cm. V prostoru mezi deskami je vakuum. Hmotnost elektronu je 9,1 ⋅ 10−31 kg, jeho náboj znáte zpaměti. Určete výstupní rychlost vB, se kterou v bodě B opouští elektrické pole.
Elektron vstupuje do elektrického pole s kinetickou energií \(\mathcal{E}_{\mathrm{C}A}=\frac12mv_A^2\). Průchodem elektrickým polem získá navíc energii \(W_\mathrm{e}=eU\). Jeho kinetická energie v bodě B je \(\mathcal{E}_{\mathrm{C}B}=\mathcal{E}_{\mathrm{C}A}+W_\mathrm{e}\). Dosazením získáváme
\[ \frac12mv_B^2 = \frac12mv_A^2 + eU\;, \]odkud vyjádříme neznámou
\[ v_B = \sqrt{v_A^2+\frac{2eU}m} = \sqrt{(10^5)^2+\frac{2\cdot1{,}6\cdot10^{-19}\cdot200}{9{,}1\cdot10^{-31}}}\,\mathrm{m/s} = 8{,}4\cdot10^6\ \mathrm{m/s}\;. \]Urychlovače částic
Už víme, že průletem mezi elektrodami s napětím \(U\) získá nabitá částice energii \(\mathcal{E}_\mathrm{C}=W_\mathrm{e}=qU\). Požadujeme-li vyšší energii, tzn. vyšší rychlost, musí být napětím \(U\) urychlena opakovaně. Technicky existují dvě řešení: zapojit více urychlovacích komor za sebou – tím vznikne lineární urychlovač, nebo trajektorii částic pomocí magnetického pole změnit v kruhovou tak, aby částice prošly urychlovací komorou vícekrát – to je princip kruhového urychlovače. Nejvýkonnější urychlovače kombinují obě tyto možnosti.
Využití urychlovačů
Zdroj

Zdroj
Zdroj

Zdroj

Zdroj
Zdroj

Zdroj

Zdroj
Na světě existuje mnoho špičkových laboratoří disponujících urychlovačem částic. Jejich posláním je zkoumat, z čeho je náš vesmír a jak funguje. Extrémním urychlením částic a jejich srážkami můžeme přivést hmotu do stavu, v němž se nacházel vesmír těsně po Velkém třesku.
Jednou z nejslavnějších je laboratoř SLAC na Stanfordově univerzitě v USA, do které putovaly celkem tři Nobelovy ceny za objevy ve fyzice elementárních částic (objev J/ψ mezonu, objev kvarkové struktury protonu, objev tauonu) a jedna Nobelova cena za chemii (eukaryotická transkripce DNA do RNA). Možná jste slyšeli o FermiLab v USA, KEK a RIKEN v Japonsku, ESRF ve Francii, DESY v Německu, …

Zdroj
Největším urychlovačem je v současnosti LHC (Large Hadron Collider) v CERNu. CERN je Evropská organizace pro jaderný výzkum se sídlem v Ženevě. Byl zde experimentálně objeven Higgsův boson, klíčová částice pro Standardní model elementárních částic. Pravděpodobně největší dopad CERNu na život běžného člověka 21. století má vytvoření počítačové sítě World Wide Web, původně zamýšlené jako komunikační prostředek mezi pracovišti částicové fyziky.

Zdroj
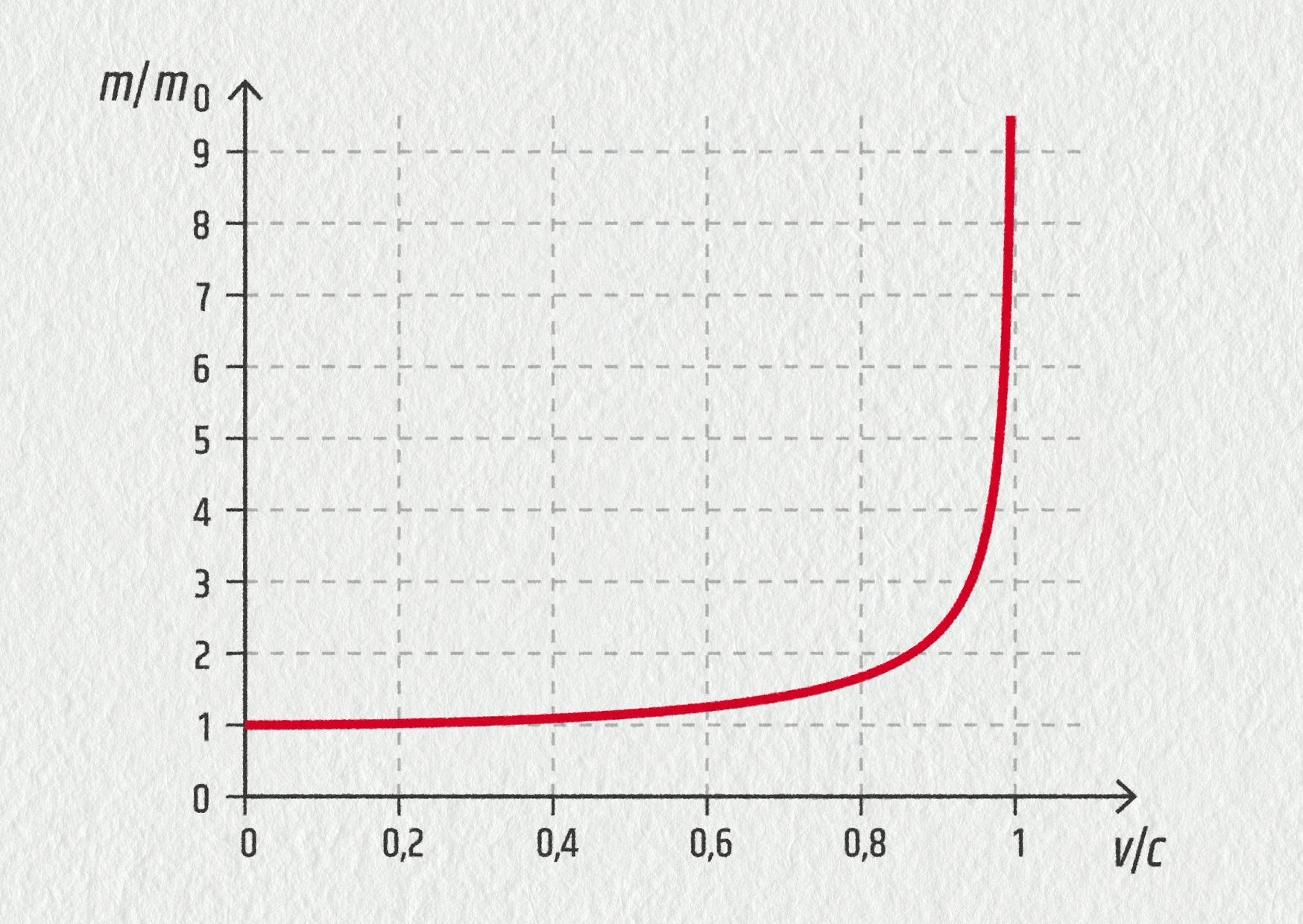
Při zvyšování kinetické energie částice v urychlovači se postupně začínají projevovat velice zvláštní vlastnosti přírody. Jednou z nejpozoruhodnějších je skutečnost, že hmotnost částic není konstantní, ale s rostoucí rychlostí se zvyšuje. Tento jev předpověděla Einsteinova speciální teorie relativity a uplatňuje se pro každou částici, jejíž rychlost se blíží rychlosti světla. Hmotnost částice \(m\) pohybující se rychlostí \(v\) je dána vztahem
\[ m = \frac{m_0}{\displaystyle\sqrt{1-\frac{v^2}{c^2}}}\;, \]kde \(m_0\) je hmotnost částice, pokud je v klidu, tzv. klidová hmotnost, a \(c\) je rychlost světla ve vakuu, \(c=299\,792\,458\ \mathrm{m/s}\simeq3{,}00\cdot10^{8}\ \mathrm{m/s}\).
Zdroj
Při rychlostech výrazně menších než je rychlost světla je přírůstek hmotnosti neměřitelný. Proto v běžném životě považujeme hmotnost za konstantní. Ovšem již při rychlosti \(v=0{,}6c\) vzroste hmotnost o 25 %. Při rychlostech blížících se rychlosti světla roste hmotnost nade všechny meze, částice těžkne a je stále obtížnější ji dále urychlovat. Při rychlosti přesně \(v=c\) by měla nekonečně velkou hmotnost, a k jejímu urychlení bychom potřebovali nekonečné množství energie. I ty nejenergetičtější částice mají vždy rychlost podsvětelnou, rychlosti světla ve vakuu se mohou hodně přiblížit, ale nikdy jí nedosáhnou. Proto rychlost \(c\) představuje pro hmotu mezní rychlost, je to jedna z nejdůležitějších konstant ve vesmíru.
Při vysokých rychlostech (obvykle se bere \(v>0{,}1c\)) nelze používat známý vzorec pro kinetickou energii \(\mathcal{E}_\mathrm{C}=\frac12mv^2\). Kinetickou energii musíme počítat jako rozdíl mezi celkovou relativistickou energií částice \(\mathcal{E}=mc^2\) a její energií klidovou \(\mathcal{E}_0=m_0c^2\). Pro kinetickou energii v našem vesmíru tedy platí přesný vztah
\[ \mathcal{E}_\mathrm{C} = mc^2-m_0c^2 = \frac{m_0}{\displaystyle\sqrt{1-\frac{v^2}{c^2}}} - m_0c^2 = m_0c^2\left(\frac1{\displaystyle\sqrt{1-\frac{v^2}{c^2}}}-1\right) \]Příklad
Protony v urychlovači LHC dosahují energií 6,5 TeV. Klidová hmotnost protonu je 1,67 ⋅ 10—27 kg. Vypočítejte, jakou rychlostí se pohybují
- podle klasické fyziky,
- ve skutečnosti.
Řešení
\[ 6{,}5\ \mathrm{TeV}=1{,}04\cdot10^{-6}\ \mathrm{J} \]a)
\[ v = \sqrt{\frac{2\mathcal{E}}{m_0}} = 3{,}53\cdot10^{10}\ \mathrm{m/s} = 118c \]Vidíme, že pro rychle se pohybující částice vzorce klasické fyziky neplatí. Ve skutečnosti totiž rychlost žádné částice nepřekročí rychlost světla ve vakuu \(c\).
b) Přímým výpočtem se můžeme přesvědčit, že klidová energie je \(\mathcal{E}_0=1{,}5\cdot10^{-10}\ \mathrm{J}\) čili o 4 řády menší než energie urychlené částice \(\mathcal{E}=mc^2=6{,}5\ \mathrm{TeV}=1{,}04\cdot10^{-6}\ \mathrm{J}\). Proto můžeme klidovou energii \(\mathcal{E}_0\) zanedbat.
\[ \mathcal{E} = \frac{m_0c^2}{\displaystyle\sqrt{1-\frac{v^2}{c^2}}} \]takže
\[ v = \sqrt{\displaystyle 1-\left(\frac{m_0c^2}{\mathcal{E}} \right)^{\!2}} = 0{,}99999999c \]
