Měření rychlosti světla
Úkol: Zjistěte rychlost šíření světla ve vakuu z doby zatmění Jupiterových měsíců.
Vybavení: Program JupLab ke stažení na http://www3.gettysburg.edu/~marschal/clea/juplab.html
Princip:
Zjišťování rychlosti světla je mimořádně obtížné, neboť světlo se šíří rychlostí, jejíž velikost o mnoho řádů převyšuje rychlosti těles, se kterými se setkáváme v běžném životě. Historicky první řádově správné měření rychlosti světla vymyslel a provedl v roce 1676 dánský astronom Ole Römer.
Využil k tomu měření časů zatmění Jupiterova měsíce Io. Jeho výsledek \(2{,}14\cdot10^8\ \mathrm{m/s}\) se sice od správné hodnoty \(c=2,99792458\cdot10^8\ \mathrm{m/s}\) liší téměř o 30 %, přesto však nezvratně dokazuje, že světlo má konečnou rychlost. Tedy že i světlo potřebuje určitý čas, aby dospělo z jednoho bodu do druhého. V tomto praktiku si Römerovu metodu vyzkoušíte pomocí počítačové simulace programem JupLab.

Zdroj
Obíhání měsíce Io kolem Jupiteru je naprosto pravidelné a může sloužit jako astronomické hodinky. Dobu, za niž Io učiní jeden oběh, a dostane se tak do stejného místa na obloze (vůči pozorovateli na Zemi), nazýváme synodickou dobou oběhu. Její hodnota je \(T_0=1{,}769861\ \mathrm{dne}\).
V ideálním případě by bylo možné dobu oběhu \(T_0\) jednoduše zjistit jako čas, který uplyne mezi dvěma po sobě následujícími zatměními čili mezi okamžiky, kdy se měsíc Io dostane za Jupiter.
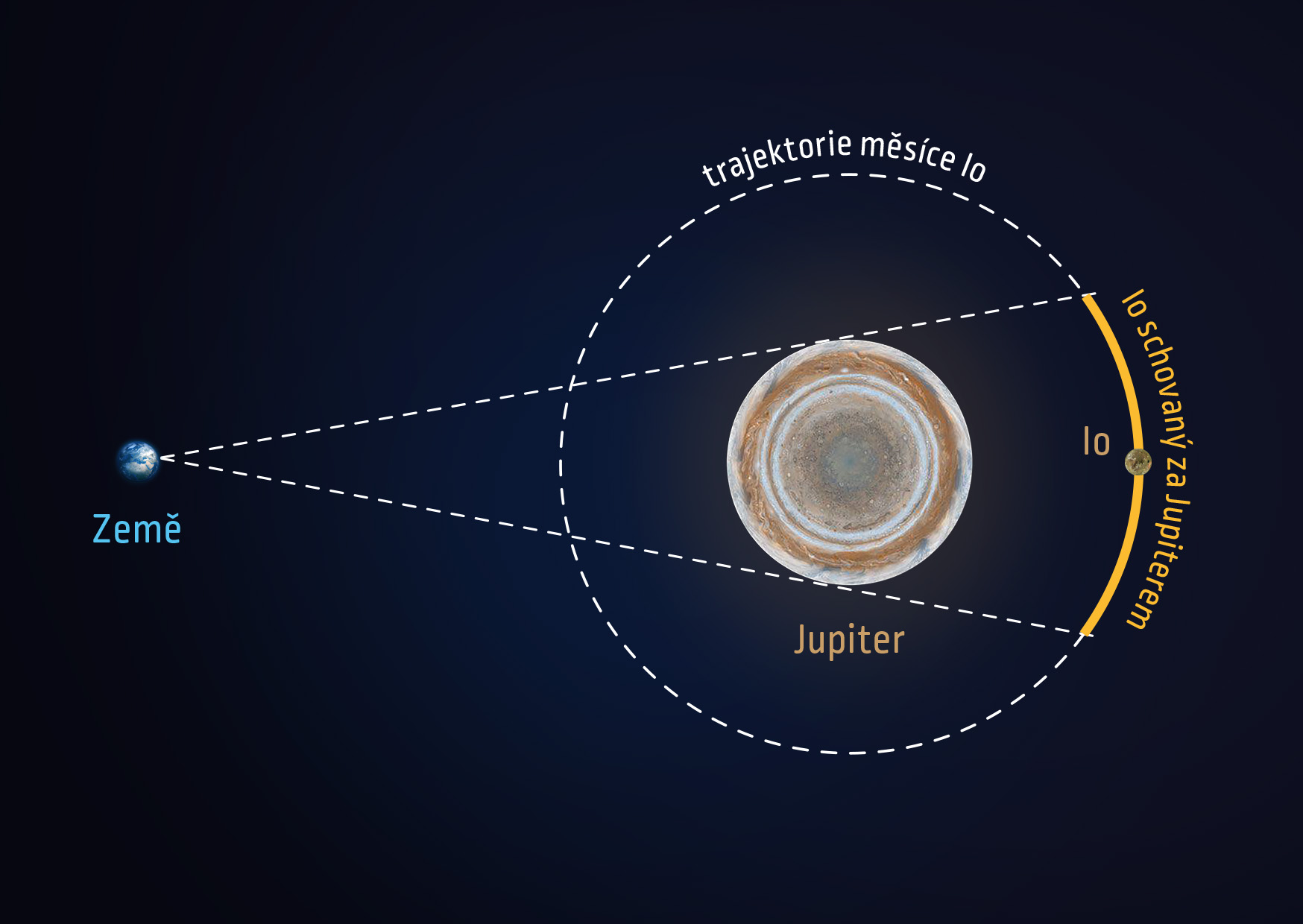
Zdroj
Ve skutečnosti nám ovšem Io někdy „zmizí“ z dalekohledu ještě dříve než za dobu \(T_0\). Měsíc Io je ze Země pozorovatelný, pokud je osvětlen slunečními paprsky. Situace, kdy se dostává do stínu vrženého Jupiterem, je znázorněna na dalším obrázku.
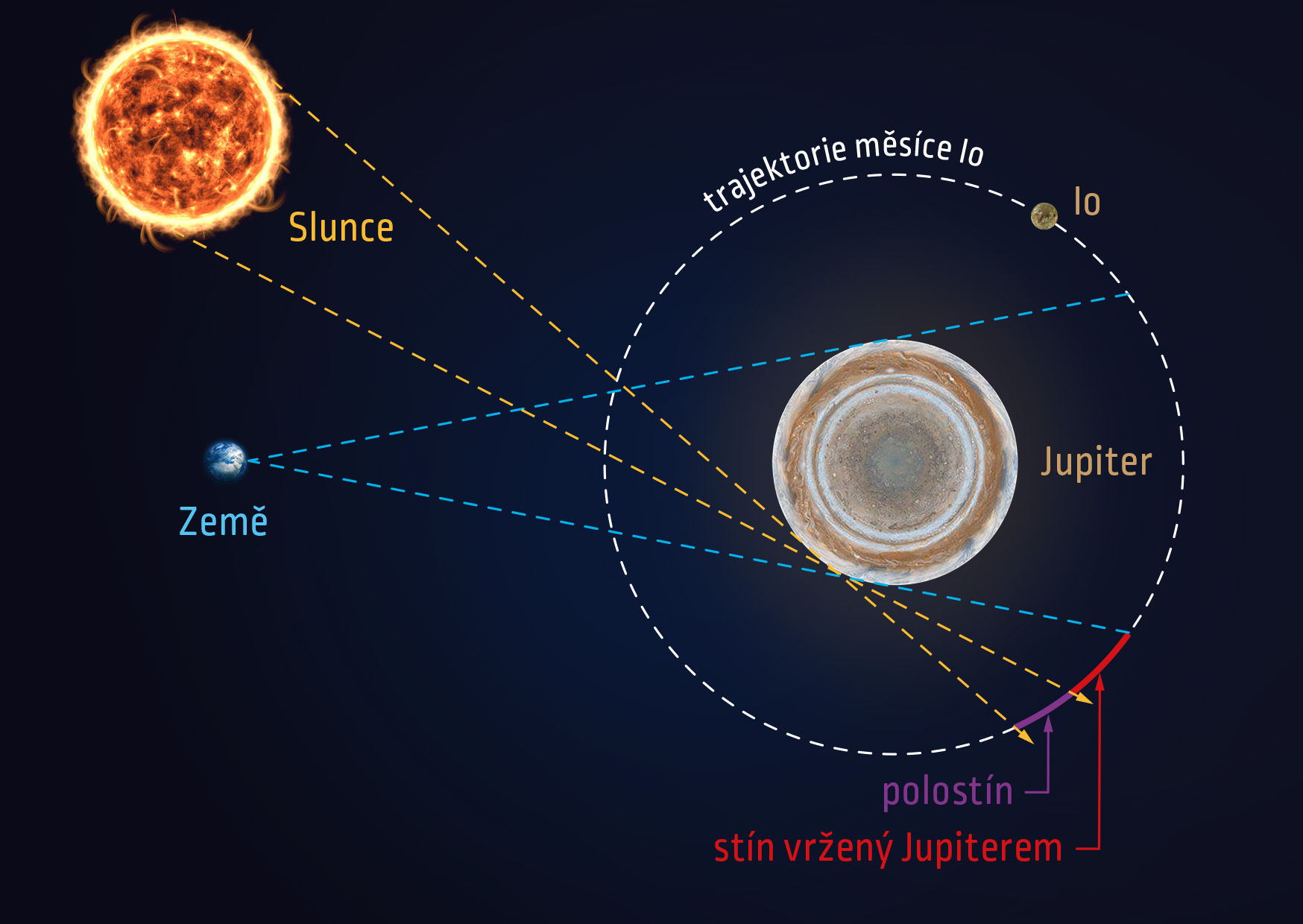
Zdroj
Abychom eliminovali jev vysvětlený na předchozím obrázku 17.57, vhodně vybereme pozorovací polohy. Paprsky rozptýlené Jupiterovým satelitem Io musí přicházet na Zemi vždy z přibližně stejného směru. První pozorování tedy provedeme, když bude Země v bodě A, zhruba dva měsíce po konjunkci Slunce s Jupiterem. Zjistíme tak přesný čas \(t_A\), kdy dojde k zatmění Io, a vzdálenost \(d_A\) – viz obrázek 17.58. Druhé měření provedeme, když bude Země v bodě B, zhruba jeden měsíc před opozicí. Zjistíme tím opět přesný čas \(t_B\), kdy dochází ke druhému zatmění, a vzdálenost \(d_B\). Mezi polohami Země A a B vykoná Io několik oběhů kolem Jupitera.
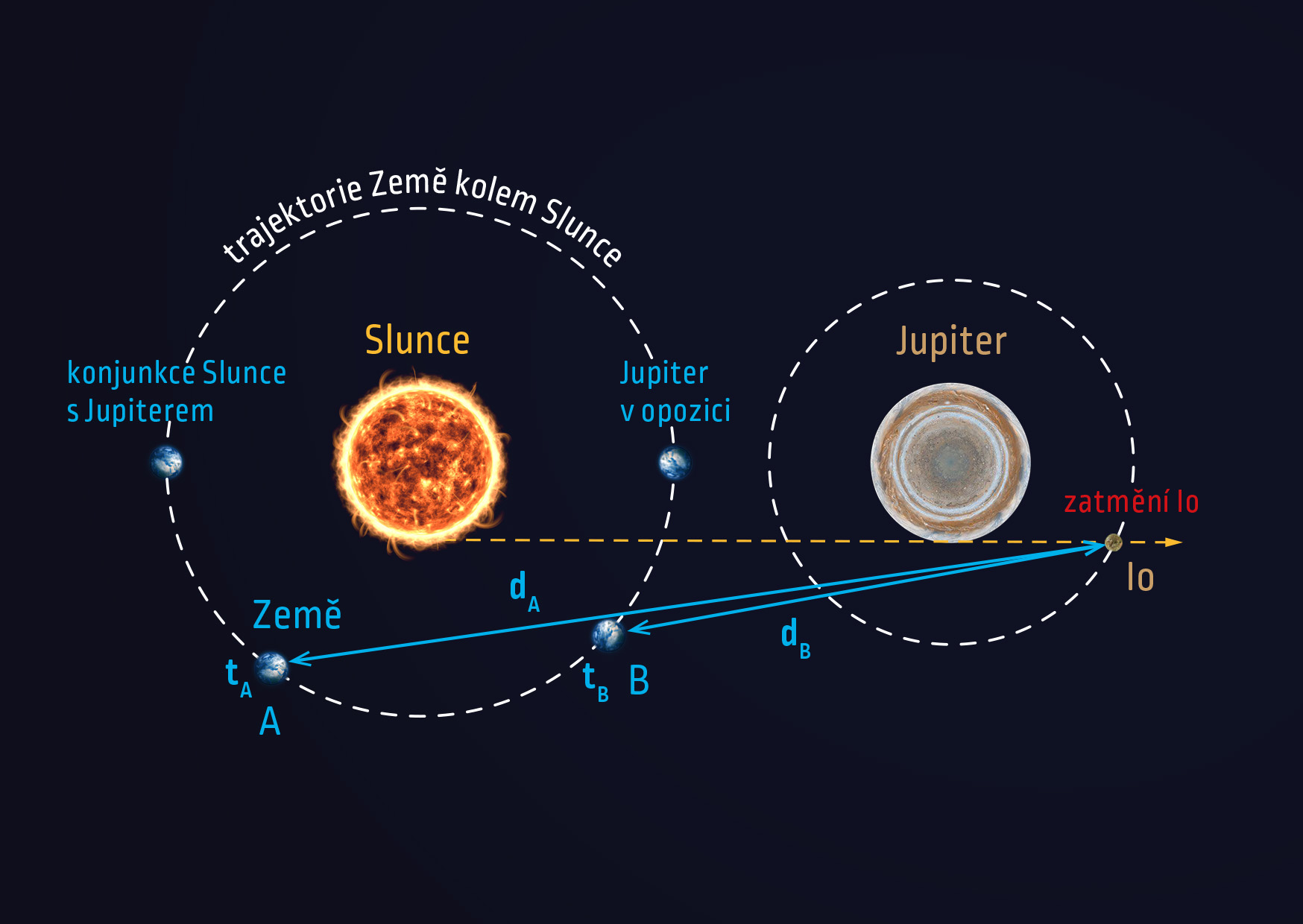
Zdroj
Při konečné rychlosti šíření světla se o tom, že došlo k zatmění měsíce, dozvíme na Zemi s určitým zpožděním. Čím bude Země od Jupitera dále, tím bude zpoždění větší. Toho použijeme k měření rychlosti světla. Poněvadž je vzdálenost \(d_A\) větší než \(d_B\), je doba šíření světla do bodu A větší než do bodu B. Proto zatmění zaregistrujeme v bodě A se zpožděním \(\Delta t\) oproti zatmění v bodě \(B\). Platí
\[ t_B-t_A = \hbox{(celé číslo)}\cdot T_0+\Delta t\;. \]Rychlost světla se pak vypočítá ze vztahu
\[ c = \frac{\Delta d}{\Delta t} = \frac{d_A-d_B}{\Delta t} = \frac{|AB|}{\Delta t}\;. \]Princip:
-
Zjistěte datum a čas, kdy je Jupiter v konjunkci a v opozici File → Observation Date → Jupiter Phenomena
Datum a čas konjunkce: …
Datum a čas opozice: …
-
Vyberte si datum přibližně dva měsíce po konjunkci a datum jeden měsíc předcházející opozici.
Datum pozorování z bodu A: …
Datum pozorování z bodu B: …
-
Změřte na sekundy přesně, kdy nastane zatmění pozorované z bodu A a bodu B. Využívejte možností programu File → Observation Date → Set Date/Time…, File → Timing → Observation Step a File → Features.
Přesné datum a čas zatmění pozorované z bodu A: \(t_A={}\)…
Přesné datum a čas zatmění pozorované z bodu B: \(t_B={}\)…
-
Zjistěte vzdálenost mezi Zemí a Jupiterem ve změřených časech \(t_A\) a \(t_B\): po kliknutí na měsíc Io v hlavním okně programu a stisknutí tlačítka Record se v novém okně zobrazí požadovaná vzdálenost.
\(d_A={}\)…
\(d_B={}\)…
Vzdálenost \(\Delta d = d_A-d_B ={}\)…
-
Kolik času uplynulo mezi A a B? \(t_A-t_B={}\)…
Zjistěte, kolikrát mezitím Io oběhl Jupiter, a dostal se tak na stejné místo na obloze. Počet oběhů (celé číslo): …
-
Vypočítejte zpoždění \(\Delta t={}\)…
-
Vypočítejte experimentální rychlost šíření světla a porovnejte výsledek se známou hodnotou.

