Struktura atomu
Z čeho je náš svět?
S myšlenkou, že náš svět je složen z miniaturních, dále nedělitelných stavebních částic zvaných atomy, přišli starořečtí myslitelé Démokritos a Leukippos v 5. století před naším letopočtem. Ve své době neměli pro svoji hypotézu žádný experimentální důkaz, jednalo se o teoretickou úvahu. Na první důkazy existence atomů a pochopení celé věci si muselo lidstvo počkat až do 20. století, kdy technika dosáhla dostatečné úrovně k jejich experimentálnímu zkoumání.
Dnes víme, že atomy nejsou nedělitelné. Skládají se z kladně nabitého jádra a záporně nabitého obalu. Jádro samotné je tvořeno dvěma druhy částic: kladnými protony a neutrálními neutrony. Částicím v jádru se souhrnně říká nukleony. Elektronový obal je oblast, kde se pohybují záporné elektrony vázané k jádru.
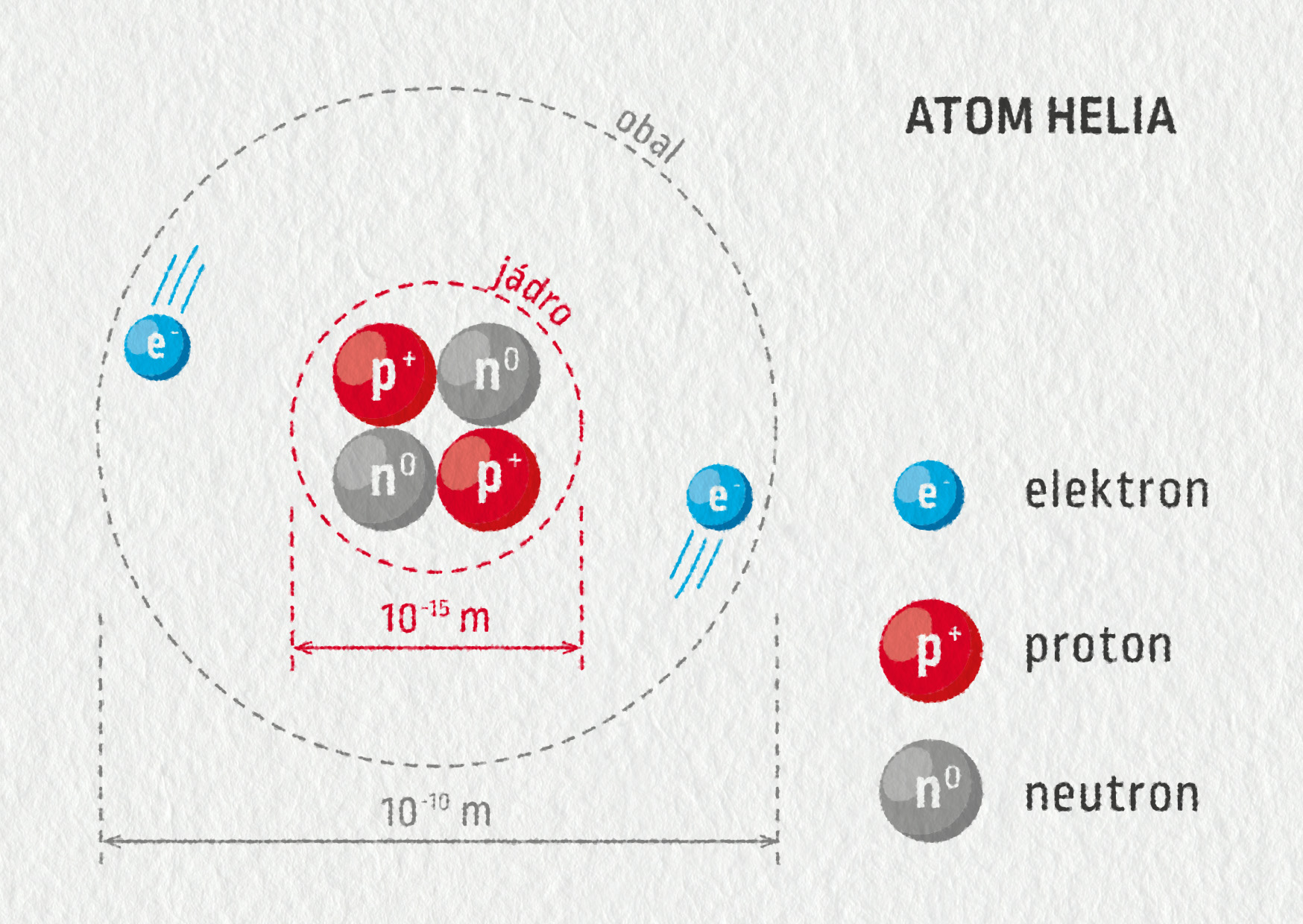
Zdroj
Obrázek 27.5 znázorňující atom helia není zcela realistický. Ve skutečnosti má jádro průměr řádově \(10^{-15}\ \mathrm{m}=1\ \mathrm{fm}\) (femtometr) a obal velikost řádově \(10^{-10}\ \mathrm{m}=0{,}1\ \mathrm{nm}\) (desetina nanometru), čili jádro je o pět řádů menší než obal. Pro představu – kdyby bylo jádro velké jako zrnko máku (řádově 1 mm), měl by elektronový obal rozměry fotbalového hřiště (řádově 100 m).
V následující tabulce jsou uvedeny nejdůležitější vlastnosti stavebních částic atomu. Můžete si povšimnout, že proton a neutron mají téměř stejnou hmotnost a jsou zhruba 1 800 krát těžší než elektron. To znamená, že hmotnost atomu je z více jak 99,9 % soustředěna v jádru, kolem něhož se pohybují lehoučké elektrony.
| částice | značka | hmotnost | náboj |
|---|---|---|---|
| proton | p+ | 1,6726 ⋅ 10−27 kg | +1,602 ⋅ 10−19 C |
| neutron | n0 | 1,6749 ⋅ 10−27 kg | 0 C |
| elektron | e− | 9,11 ⋅ 10−31 kg | −1,602 ⋅ 10−19 C |
Elektrický náboj protonu \(q_\mathrm{p}=+1{,}602\cdot10^{-19}\ \mathrm{C}\) se nazývá elementární náboj a je až na znaménko stejně velký jako náboj elektronu. Proto je u neutrálních atomů počet protonů v jádru stejný jako počet elektronů v obalu.
Rozdělení atomů
K jednoznačnému popisu složení atomů se ve fyzice a chemii používá označení symbolem \({}^A_ZX\), kde levý dolní index \(Z\) je protonové číslo (počet protonů), levý horní index \(A\) je nukleonové číslo (počet protonů plus počet neutronů) a \(X\) je značka odpovídajícího chemického prvku. Například atom železa \({}^{56}_{26}\mathrm{Fe}\) je složen z 26 protonů, 30 neutronů a 26 elektronů. Jak uvidíme později, protonové a nukleonové číslo nebylo vybráno náhodně – jsou to čísla, která se zachovávají při jaderných reakcích.
V současnosti je známo přes 3 000 různých druhů atomů. Je zvykem je třídit do následujících kategorií.
Pojmem nuklid označujeme určitý druh atomů. Všechny atomy tvořící daný nuklid mají stejné protonové číslo a stejné nukleonové číslo. Například atomy se šesti protony a osmi neutrony tvoří nuklid uhlíku \({}^{14}_{\hphantom{0}6}\mathrm{C}\), atomy se 17 protony a 18 neutrony tvoří nuklid chloru \({}^{35}_{17}\mathrm{C}\). V přírodě existuje 252 stabilních nuklidů a přibližně 85 nestabilních (radioaktivních). Ostatní známé nuklidy byly vytvořeny uměle.
Chemický prvek je soubor atomů o stejném protonovém čísle \(Z\). Protonové číslo \(Z\) tedy určuje, o jaký prvek jde. Tyto atomy se mohou vzájemně lišit nukleonovým číslem. V přírodě existuje 92 chemických prvků, nejlehčím je vodík \({}_1\mathrm{H}\), nejtěžším je uran \({}_{92}\mathrm{U}\). Prvky s protonovým číslem \(Z>92\) se nazývají transurany, byly vytvořeny uměle a jsou radioaktivní. Protonové číslo \(Z\) současně udává též počet elektronů v obalu neutrálního atomu, a tím pádem jeho chemické vlastnosti – všechny atomy téhož chemického prvku mají totožné chemické vlastnosti.
Izotopy jsou nuklidy téhož chemického prvku. Mají tedy stejné protonové číslo \(Z\), ale liší se počtem neutronů. Chemický prvek vodík má tři izotopy: \({}_1^1\mathrm{H}\), \({}_1^2\mathrm{H}\) (zvaný deuterium), \({}_1^3\mathrm{H}\) (zvaný tritium, radioaktivní). Chemický prvek uran má 28 izotopů, z nichž praktický význam mají izotop \({}_{\hphantom{0}92}^{234}\mathrm{U}\) (radioaktivní, přispívá k záření zemské kůry), izotop \({}_{\hphantom{0}92}^{235}\mathrm{U}\) (využívá se při štěpení v jaderných elektrárnách) a izotop \({}_{\hphantom{0}92}^{238}\mathrm{U}\) (téměř stabilní, nejhojněji zastoupen).
Z kolika částic je tvořeno jádro atomu stříbra \({}_{\hphantom{0}47}^{107}\mathrm{Ag}\)?
Atomy patřící témuž chemickému prvku mají totožné chemické vlastnosti. Proto izotopy určitého prvku reagují stejně a chemickými procesy je nelze oddělit. Existuje nějaký jiný způsob, jak to provést?
Nuklidy se vzájemně liší počtem neutronů, tedy hmotností. Těžší nuklidy mají větší setrvačnost. Laboratorně lze jejich separaci provést v hmotnostním spektrometru, průmyslově se provádí v odstředivkách.

Zdroj

Zdroj
Hmotnost jádra
Jak vypočítat hmotnost jádra?
Když budete z Lega skládat nějaký složitější model, bude vždy hmotnost vaší stavby stejná jako součet hmotností kostek, které jste použili. Mohli bychom předpokládat, že toto pravidlo bude fungovat i pro atomy.
Pro jádro, obal a celý atom tato úvaha skutečně platí. V mezích přesnosti dosavadních měření je hmotnost celého atomu \(m_\mathrm{at}\) rovna součtu hmotnosti jádra \(m_\mathrm{j}\) a součtu hmotností elektronů \(m_\mathrm{e}\) v atomovém obalu. Můžeme psát
\[ m_\mathrm{at} = m_\mathrm{j} + Zm_\mathrm{e}\;, \]kde \(Z\) (protonové číslo) značí počet elektronů v obalu. Stačí tedy přesně zjistit hmotnost celého atomu a použít uvedený vztah.
Podobnou úvahu bohužel nelze použít pro samotné jádro a nukleony: ve skutečnosti je totiž hmotnost jádra vždy menší než prostý součet hmotností oddělených částic, z nichž je složeno. Jedná se o experimentální fakt, který postupně vysvětlíme.

Zdroj
Rozdíl mezi celkovou hmotností oddělených nukleonů a hmotností jádra se nazývá hmotnostní schodek jádra. Značí se \(\Delta m\) a vypočítáme jej podle definice
\[ \Delta m = Zm_\mathrm{p} + (A-Z)m_\mathrm{n} - m_\mathrm{j}\;, \]kde \(Z\) je protonové číslo, \(A\) nukleonové číslo, \(m_\mathrm{p}\) hmotnost protonu, \(m_\mathrm{n}\) hmotnost neutronu a \(m_\mathrm{j}\) hmotnost jádra. Hmotnostní schodek představuje zhruba 1 % celkové hmotnosti jádra.
Vypočítejte hmotnostní schodek jádra helia \({}_2^4\mathrm{He}\). Zadané hodnoty:
\[\begin{aligned} m_\mathrm{at} &= 6{,}6464\cdot10^{-27}\ \mathrm{kg}\\ m_\mathrm{p} &= 1{,}6726\cdot10^{-27}\ \mathrm{kg}\\ m_\mathrm{n} &= 1{,}6749\cdot10^{-27}\ \mathrm{kg}\\ m_\mathrm{e} &= 9{,}11\cdot10^{-31}\ \mathrm{kg}\\ \end{aligned}\]Atom helia 4 je složen ze dvou protonů, dvou neutronů a dvou elektronů v obalu.
Přímým dosazením získáme hmotnost jádra
\[\begin{aligned} m_\mathrm{j} &= m_\mathrm{at} - Zm_\mathrm{e}\\ &= 6{,}6464\cdot10^{-27}\ \mathrm{kg} - 2\cdot9{,}11\cdot10^{-31}\ \mathrm{kg}\\ &= 6{,}6446\cdot10^{-27}\ \mathrm{kg}\;. \end{aligned}\]Hmotnostní schodek jádra vypočítáme jako rozdíl celkové hmotnosti jednotlivých nukleonů a skutečné hmotnosti jádra
\[\begin{aligned} \Delta m &= Zm_\mathrm{p} + (A-Z)m_\mathrm{n} - m_\mathrm{j}\\ &= 2\cdot1{,}6726\cdot10^{-27}\ \mathrm{kg} - (4-2)\cdot1{,}6749\cdot10^{-27}\ \mathrm{kg} - 6{,}6446\cdot10^{-27}\ \mathrm{kg}\\ &= 5{,}04\cdot10^{-29}\ \mathrm{kg}\;.\\ \end{aligned}\]Hmotnostní schodek jádra helia představuje přibližně 0,8 % celkové hmotnosti atomu. Všimněte si, že zde odečítáme dvě blízká čísla. Aby nevznikala chyba zaokrouhlováním, museli jsme u zadaných údajů ponechat všechny platné číslice až do řádu 0,000 1 ⋅ 10−27 kg.
Atomová hmotnostní konstanta
V jaderné fyzice a chemii je obvyklé vyjadřovat hmotnosti atomů a jader v násobcích atomové hmotnostní konstanty u. Vysvětlena byla v kapitole 10, na tomto místě si připomeneme její základní vlastnosti.
Atomová hmotnostní konstanta u je rovna jedné dvanáctině hmotnosti atomu uhlíku \({}^{12}_{\hphantom{0}6}C\). Tato konstanta tedy odpovídá přibližně hmotnosti jednoho nukleonu. Potom ovšem hmotnost atomu nebo jádra vyjádřená v násobcích u (tzv. atomová relativní hmotnost) je číselně blízká počtu nukleonů. Hodnota atomové hmotnostní konstanty vyjádřená v kilogramech je
\[ 1\ \mathrm{u} = 1{,}660539\cdot10^{-27}\ \mathrm{kg}\;. \]Jak ukazuje následující příklad, s využitím atomové hmotnostní konstanty se vyhneme faktoru 10−27 a zápis výpočtů se mírně zjednoduší.
Vypočítejte hmotnostní schodek jádra železa \({}^{56}_{26}\mathrm{Fe}\). Zadané hodnoty:
\[\begin{aligned} m_\mathrm{at} &= 55{,}9349\ \mathrm{u}\\ m_\mathrm{p} &= 1{,}00728\ \mathrm{u}\\ m_\mathrm{n} &= 1{,}00866\ \mathrm{u}\\ m_\mathrm{e} &= 5{,}486\cdot10^{-4}\ \mathrm{u}\\ \end{aligned}\]Atom železa \({}^{56}_{26}\mathrm{Fe}\) je tvořen 26 protony, 30 neutrony a 26 elektrony.
Hmotnost jeho jádra je
\[\begin{aligned} m_\mathrm{j} &= m_\mathrm{at} - Zm_\mathrm{e}\\ &= 55{,}9349\ \mathrm{u} - 26\cdot5{,}486\cdot10^{-4}\ \mathrm{u}\\ &= 55{,}9206\ \mathrm{u}\;.\\ \end{aligned}\]Hmotnostní schodek jádra železa je
\[\begin{aligned} \Delta m &= Zm_\mathrm{p} + (A-Z)m_\mathrm{n} - m_\mathrm{j}\\ &= 26\cdot1{,}00728\ \mathrm{u} + 30\cdot1{,}00866\ \mathrm{u} - 55{,}9206\ \mathrm{u}\\ &= 0{,}5302\ \mathrm{u}\\ &= 8{,}804\cdot10^{-29}\ \mathrm{kg}\;.\\ \end{aligned}\]Souvislost mezi hmotností a energií
V roce 1905 přišel Albert Einstein s fenomenálním objevem. V rámci speciální teorie relativity odvodil, že hmotnost tělesa a energie v něm uložená nejsou nezávislé, nýbrž souvisí spolu jednoduchým vztahem.
Souvislost mezi hmotností a energií
\[ E = mc^2 \]\(E\) – celková energie tělesa v J
\(m\) – hmotnost tělesa v kg
\(c\) – rychlost světla ve vakuu \(c=299\,792\,458\ \mathrm{m/s}\approx3{,}00\cdot10^8\ \mathrm{m/s}\)
V celkové energii \(E\) tělesa je započítána jeho kinetická energie, potenciální energie, vnitřní energie (tepelná energie, energie chemických a jaderných vazeb) a klidová energie. Klidová energie \(E_0=m_0c^2\) je energie spojená se samotnou existencí hmoty (její klidovou hmotností \(m_0\)). Za běžných podmínek je klidová energie o mnoho řádů větší než příspěvky ostatních forem energie. Například v jednom gramu hmoty je uložena klidová energie \(E_0=0{,}001\ \mathrm{kg}\cdot(3\cdot10^8\ \mathrm{m/s})^2=9\cdot10^{13}\ \mathrm{J}\), zatímco jeho kinetická energie při rychlosti 1000 m/s by byla pouze 5 ⋅ 102 J, čili přibližně dvěstěmiliardkrát menší než klidová.
Einsteinova rovnice ukazuje, že v hmotě je uložena obrovská energie. Kdybychom ji dokázali uvolnit a přeměnit například na elektrickou energii, byl by zdroj energie pro lidstvo zajištěn. Ve skutečnosti má největší část energie podobu klidové energie stavebních částic – dokud budou tyto částice existovat, ponesou v sobě klidovou energii, a zůstane nám tak nedosažitelná. K výrobě elektrické energie tedy nezbývá než využívat jiných forem energie. Jak uvidíme dále, jedním z nejbohatších zdrojů je energie jaderných vazeb.
Podle rovnice \(E=mc^2\) nemůže být hmotnost tělesa přísně vzato konstantní a roste například při urychlování nebo zahřívání tělesa úměrně s nárůstem celkové energie. Jedná se o zcela revoluční poznatek, v příkrém rozporu s představou o zachování hmotnosti.
Změna hmotnosti částic se skutečně pozoruje při jejich urychlování na rychlosti blízké rychlosti světla ve vakuu a může dosáhnout až tisícinásobku klidové hmotnosti – viz poznámka na okraj v oddílu Urychlování částic v kapitole 18.
Naopak změny hmotnosti makroskopických těles jsou za běžných podmínek neměřitelně malé, protože klidová energie je o mnoho řádů vyšší než ostatní druhy energie. Například hmotnost tělesa vzroste urychlením z klidu na rychlost 100 km/h jen o 4 ⋅ 10−13 procenta. Podobně hmotnost vody se při ohřevu o 50 °C zvýší jen o 2 ⋅ 10−10 procenta. Při běžných výpočtech tedy považujeme hmotnost těles za stálou.
Pokud se během chemických reakcí uvolňuje energie do prostředí například ve formě tepelného záření, musí být klidová hmotnost látek reagujících větší než klidová hmotnost látek vznikajících. Principiálně vzato se tedy hmotnost nezachovává. Ovšem rozdíl mezi uvažovanými hmotnostmi představuje v případě chemických reakcí jen řádově miliardtinu klidové hmotnosti, takže je zcela neměřitelný. Proto v chemii můžeme používat „zákon“ zachování hmotnosti. V případě jaderných reakcí představuje změna hmotnosti až 1 % klidové energie, což zanedbat nelze, a hmotnosti musíme počítat přesně s využitím Einsteinova vztahu.
Vazebná energie
Proč drží jádra pohromadě?
Jádra atomů jsou tvořena kladnými protony a neutrálními neutrony. Tyto částice mají nenulovou hmotnost a přitahují se gravitační silou \(\Vec{F}_\mathrm{g}\). Proton a neutron na sebe elektricky nepůsobí, ovšem kladné protony se vzájemně odpuzují elektrickou silou \(\Vec{F}_\mathrm{e}\). Abychom získali představu, která ze sil je v jádru významnější, vypočítejme poměr jejich velikostí pro působení mezi protony (dosazení v základních jednotkách SI):
\[\begin{aligned} \frac{F_\mathrm{g}}{F_\mathrm{e}} &= \frac{\displaystyle k\frac{q_\mathrm{p}q_\mathrm{p}}{r^2}}{\displaystyle G\frac{m_\mathrm{p}m_\mathrm{p}}{r^2}} = \frac{kq_\mathrm{p}^2}{Gm_\mathrm{p}^2}\\ &= \frac{8{,}99\cdot10^9\cdot(1{,}60\cdot10^{-19})^2}{6{,}67\cdot10^{-11}\cdot(1{,}67\cdot10^{-27})^2}\\ &= 1{,}24\cdot10^{36}\;.\\ \end{aligned}\]Zjišťujeme tedy, že elektrické odpuzování je o 36 řádů silnější než gravitační přitahování (jeho velikost je podobná i pro působení mezi protonem a neutronem). Podle tohoto výpočtu by měla elektrická síla jádro roztrhat a v přírodě by vůbec žádná jádra neměla existovat. Tuto úvahu nezvrátí ani přítomnost elektronového obalu (vzdálenost mezi protony je o 5 řádů menší než vzdálenost mezi protony a elektrony, takže odpuzování mezi protony je podle Coulombova zákona o 10 řádů silnější než přitahování mezi protony a elektrony).
Jelikož je existence jader experimentálně potvrzena, musí mezi nukleony působit ještě nějaká jiná přitažlivá síla, která překoná elektrické odpuzování mezi protony. Touto jadernou silou je tak zvaná silná interakce. Je to další druh působení mezi částicemi, nezávislý na gravitaci a elektromagnetismu, jedna ze čtyř známých základních interakcí mezi elementárními částicemi. Silná interakce je vždy přitažlivá, působí mezi nukleony a má velice krátký dosah – typicky 10−15 m. Znamená to, že pokud se dva nukleony vzdálí na více jak 10−15 m, přestanou se vzájemně „cítit“, přesněji řečeno, intenzita silné interakce exponenciálně poklesne k nule.
V současné době jsou známy čtyři základní fyzikální interakce – čtyři nezávislé způsoby, jak na sebe mohou elementární částice působit: gravitační, elektromagnetická, silná a slabá interakce. Každá interakce se týká jiné vlastnosti elementárních částic, například gravitace je projevem hmotnosti, elektromagnetické jevy jsou projevem elektrického náboje, silná interakce projevem barevného náboje a slabá interakce projevem „vůně“. Vztahy mezi elementárními částicemi a jejich působením popisuje tzv. Standardní model – fyzikální teorie elementárních částic, která je v současnosti považována za správnou.
Vazebná energie jádra
Nukleony jsou v jádru vázány silnou interakcí. S ní je spojena potenciální energie, jejíž velikost nejsnadněji vyjádříme pomocí energie potřebné k přerušení jaderných vazeb.
Vazebná energie jádra \(E_\mathrm{v}\) je rovna energii, kterou musíme jádru dodat, abychom je rozdělili na jednotlivé nukleony. Při tom předpokládáme, že původní jádro i oddělené nukleony jsou v klidu. Analogicky bychom mohli říci, že vazebná energie jádra je energie, která se uvolní do okolního prostředí, když oddělené nukleony vytvoří odpovídající jádro. Jádro má menší energii než samostatné nukleony, a je tedy stabilnější.
V následující poznámce odvodíme vztah pro výpočet vazebné energie:
\[ E_\mathrm{v} = \Delta m\,c^2\;, \]kde \(\Delta m\) je hmotnostní schodek jádra a \(c\) rychlost světla ve vakuu.
Uvažujeme pouze klidové energie. Podle definice je vazebná energie \(E_\mathrm{v}\) rovna energii, kterou musíme dodat jádru o energii \(E_\mathrm{j}\), abychom je rozdělili na jednotlivé nukleony, které mají dohromady energii \(E_\mathrm{jn}\). Platí
\[ E_\mathrm{j} + E_\mathrm{v} = E_\mathrm{jn} \quad\hbox{neboli}\quad E_\mathrm{v} = E_\mathrm{jn} - E_\mathrm{j}\;. \]S využitím Einsteinova vztahu \(E=mc^2\) získáváme vztah
\[ E_\mathrm{v} = m_\mathrm{jn}c^2 - m_\mathrm{j}c^2 \]a po rozepsání hmotnosti oddělených nukleonů
\[ E_\mathrm{v} = [Zm_\mathrm{p} + (Z-A)m_\mathrm{n} - m_\mathrm{j}]c^2\;, \]kde zřejmě výraz v hranaté závorce značí hmotnostní schodek jádra, tedy
\[ E_\mathrm{v} = \Delta m\,c^2\;. \]Hmotnostní schodek je důsledkem existence vazby mezi nukleony. Vazebná energie představuje přibližně 1 % klidové energie jádra.
V jaderné fyzice se vazebné energie obvykle vyjadřují v megaelektronvoltech, převodní vztah známe již z kapitoly 18:
\[ 1\ \mathrm{MeV} = 10^6\ \mathrm{eV} = 1{,}602\cdot10^{-13}\ \mathrm{J}\;. \]Stabilita jader
Stabilitu jader nejsnáze posoudíme pomocí energie, kterou je třeba v průměru vynaložit na uvolnění jednoho nukleonu z jádra. Definujeme proto vazebnou energii připadající na jeden nukleon \(E_A\) předpisem
\[ E_A = \frac{E_\mathrm{v}}A\;, \]kde \(E_\mathrm{v}\) je vazebná energie jádra a \(A\) nukleonové číslo.
Čím větší je \(E_A\), tím „pevněji drží“ nukleony při sobě, tím více energie potřebujeme k jejich oddělení, a tím je jádro stabilnější.
Porovnejte stabilitu jader \({}^4_2\mathrm{He}\) a \({}^{56}_{26}\mathrm{Fe}\).
Stabilitu jader můžeme porovnávat pomocí vazebné energie připadající na jeden nukleon – čím je \(E_A\) větší, tím je jádro stabilnější.
K výpočtu použijeme hmotnostní schodky získané v předchozích řešených příkladech.
Helium:
\[\begin{aligned} \Delta m &= 5{,}04\cdot10^{-29}\ \mathrm{kg}\\ E_\mathrm{v} &= \Delta m\cdot c^2 = 5{,}04\cdot10^{-29}\ \mathrm{kg}\cdot(3\cdot10^8\ \mathrm{m/s})^2 = 4{,}54\cdot10^{-12}\ \mathrm{J} = 28{,}3\ \mathrm{MeV}\\ E_A &= \frac{E_\mathrm{v}}A = \frac{28{,}3\ \mathrm{MeV}}4 = 7{,}08\ \mathrm{MeV}\\ \end{aligned}\]Analogicky pro železo:
\[\begin{aligned} \Delta m &= 8{,}80\cdot10^{-28}\ \mathrm{kg}\\ E_\mathrm{v} &= 7{,}92\cdot10^{-11}\ \mathrm{J} = 494\ \mathrm{MeV}\\ E_A &= 8{,}83\ \mathrm{MeV}\\ \end{aligned}\]Jádro železa je tedy stabilnější než jádro helia.
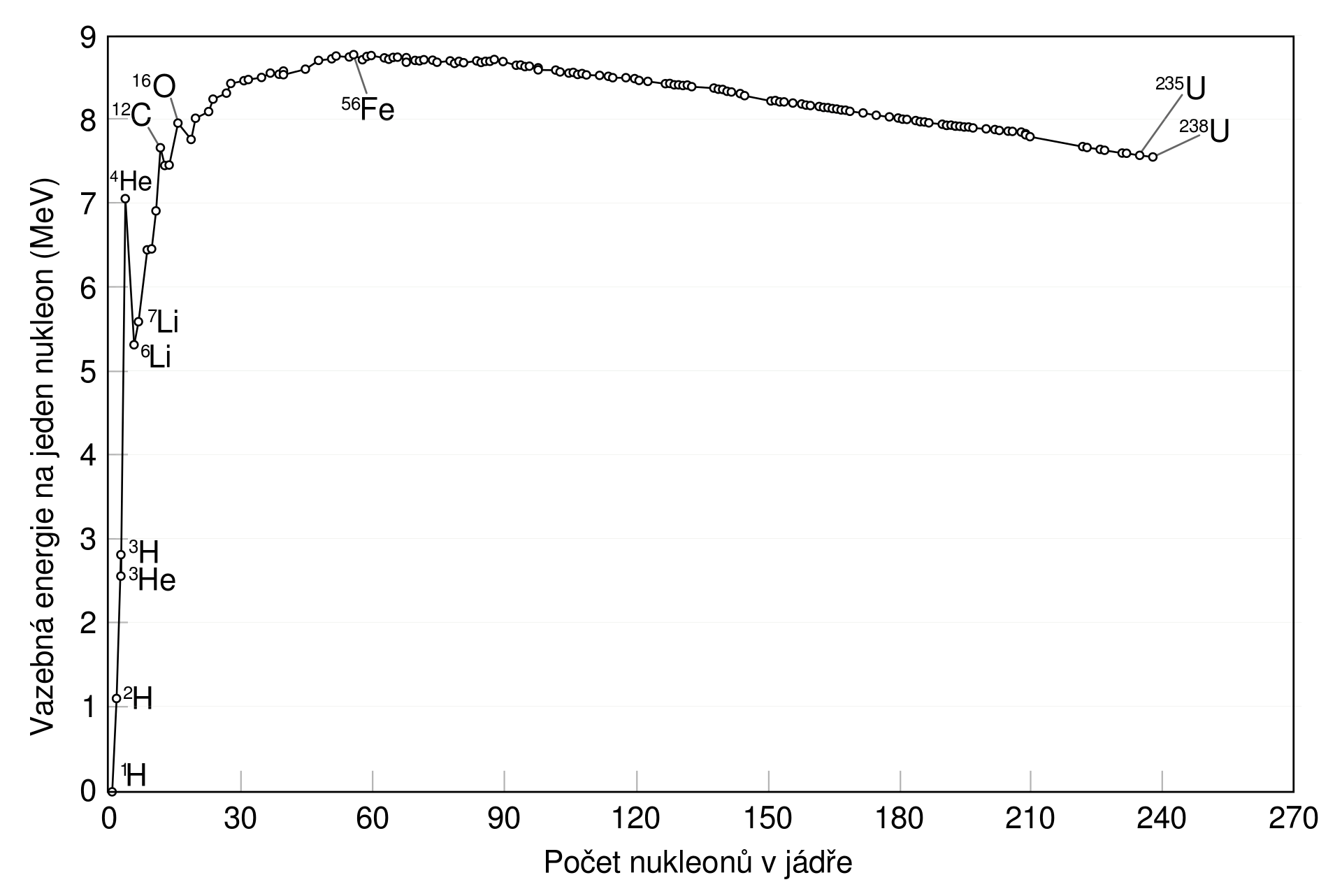
Zdroj
Podobně jako v příkladu 3 bychom mohli spočítat vazebnou energii připadající na nukleon pro každé jádro. Obrázek 27.9 ukazuje výsledek pro nejstabilnější stabilní nuklidy chemických prvků. Jádrem vodíku \({}^1\mathrm{H}\) je pouhý proton, žádná jaderná vazba se zde nevyskytuje, tudíž jeho \(E_A=0\ \mathrm{MeV}\). Nejstabilnějším nuklidem je železo \({}^{56}_{26}\mathrm{Fe}\), jehož \(E_A=8{,}83\ \mathrm{MeV}\). Na základě obrázku 27.9 můžeme též vyvodit, které jaderné reakce vedou k uvolňování energie, a jsou tedy potenciálním zdrojem energie pro lidstvo.
Slučováním jader lehkých prvků (až po železo) bude stabilita nukleonů růst a do okolí se bude uvolňovat energie. To skutečně nastává při termojaderné syntéze v nitrech hvězd, kde se lehká jádra slučují na těžší.
Štěpení těžkých jader na lehčí (až po železo) vede též ke vzrůstu stability a uvolňování energie. Štěpení uranu se využívá v jaderných reaktorech.
Oba tyto procesy prozkoumáme podrobněji v podkapitole Umělé reakce.
Proč je v přírodě jen omezený počet stabilních nuklidů?
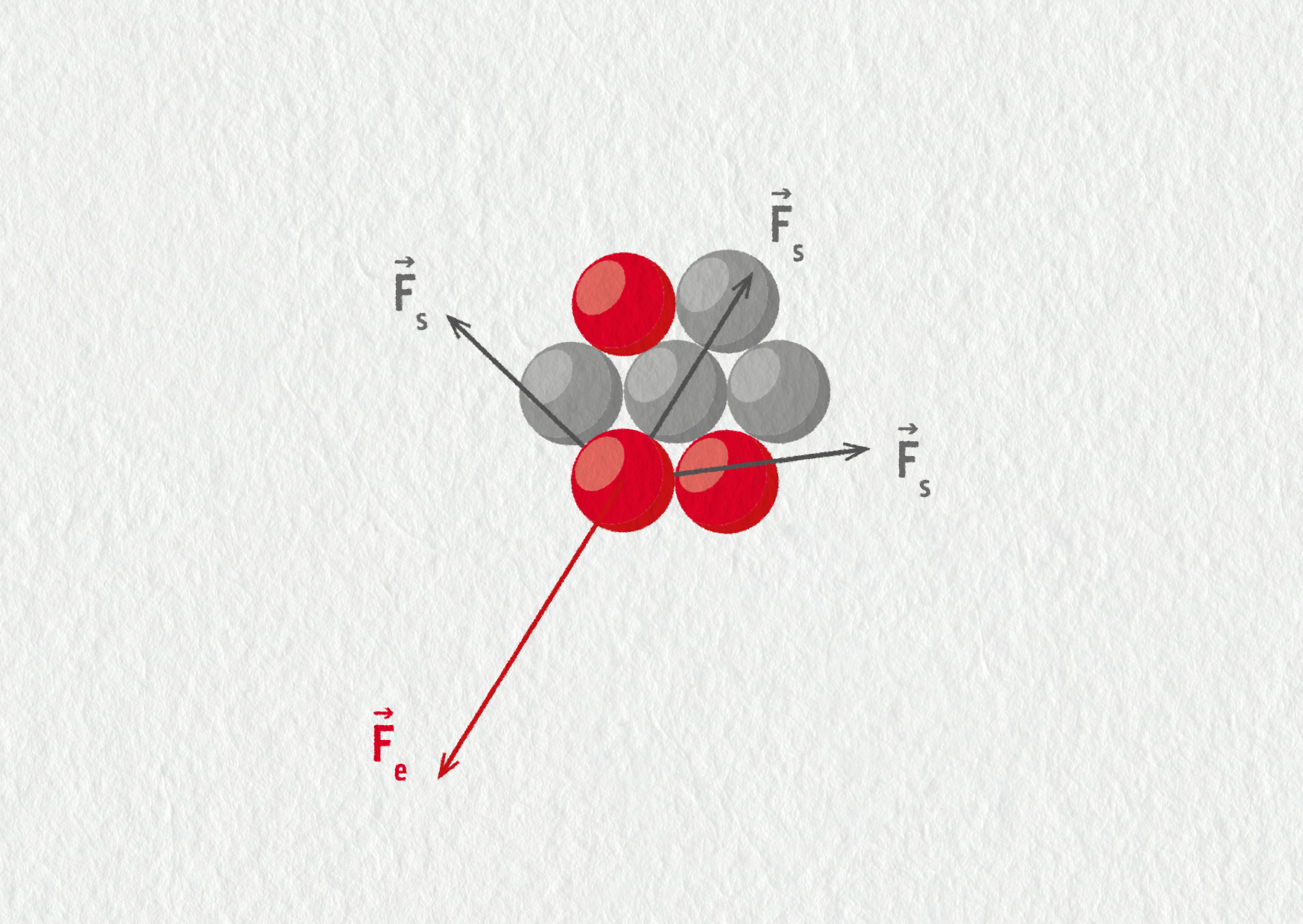
Zdroj
Silná interakce je krátkodosahová a působí bez rozdílu mezi protony a neutrony. Přidáváním dalších částic do jádra se přitahování mezi sousedy (silná interakce) téměř nezvětšuje, ovšem s každým dalším protonem roste elektrické odpuzování a klesá stabilita. Přidáváním neutronů se sice zvětšuje střední vzdálenost mezi protony, ale tyto neutrony postupně obsazují vyšší energetické hladiny, jsou slaběji vázány, což opět vede ke snížení stability. Logicky musí nastat mez, kdy elektrické odpuzování převáží nad silnou interakcí. To nastává právě pro bismut \({}^{209}_{\hphantom{0}83}\mathrm{Bi}\). Všechna jádra s \(Z>83\) nebo s \(A>209\) jsou nestabilní a rozpadají se radioaktivními procesy. Jim je věnován následující oddíl.
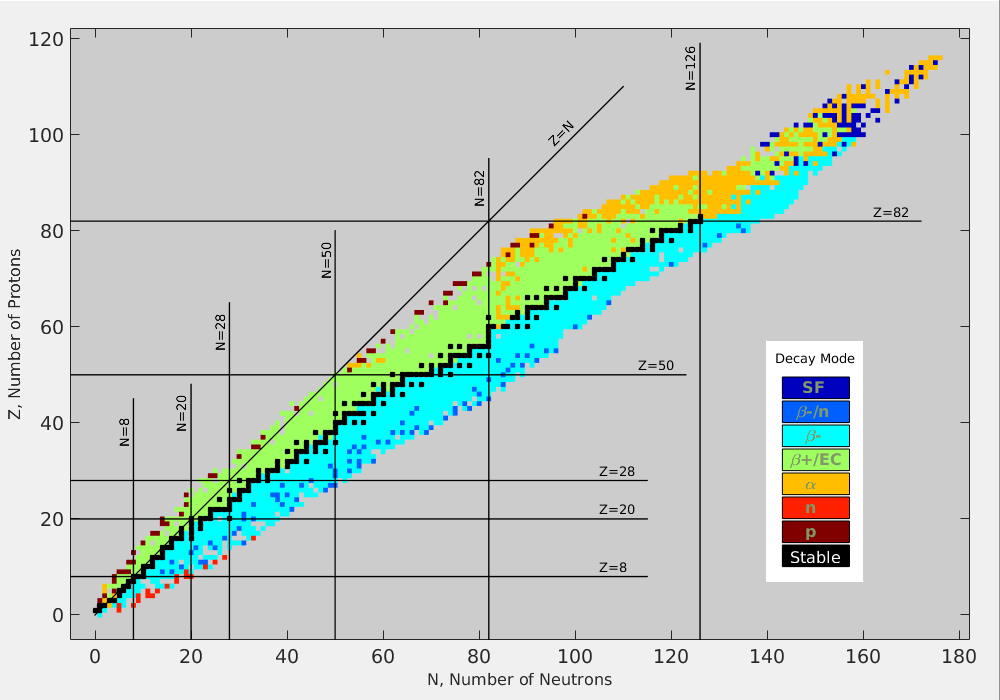
Zdroj

