Tahová síla pružiny

Cílem této krátké a jednoduché aktivity je experimentálně prozkoumat, jak síla, kterou táhne pružina, souvisí s její deformací. Budete potřebovat tažnou nepředepjatou pružinu, stojan, sadu závaží a délkové měřidlo.

21.4 – Měření tahové síly pružiny.
Zdroj

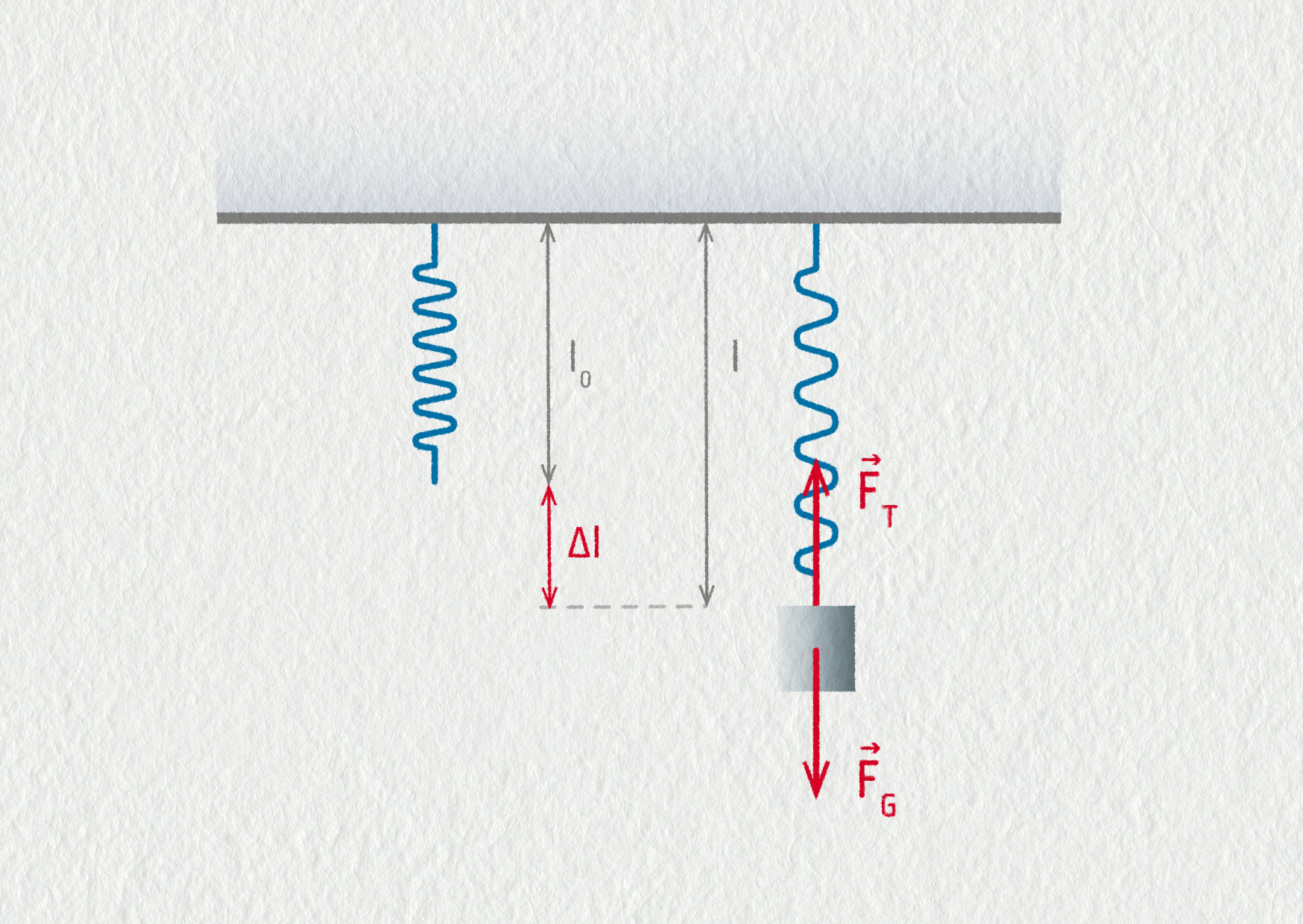
Označení veličin v obrázku 21.4:

\(l_0\) – klidová délka pružiny,
\(l\) – délka deformované pružiny,
\(\Delta l\) – prodloužení pružiny,
\(\Vec{F}_\mathrm{G}\) – tíhová síla,
\(\Vec{F}_\mathrm{T}\) – tahová síla pružiny.

Postup:

Pružinu zavěste na stojan a změřte její klidovou délku \( l_\mathrm{0} \).
Na pružinu postupně zavěšujte různá závaží o známé hmotnosti \( m \) a pokaždé změřte její délku v deformovaném stavu \( l \). Hodnoty zapisujte do tabulky.
Setrvává-li závaží v klidu, tíhová síla \(\Vec{F}_\mathrm{G}\) se přesně vyruší s tahovou silou pružiny \(\Vec{F}_\mathrm{T}\). K naměřeným datům v tabulce dopočítejte tahovou sílu pružiny \(\Vec{F}_\mathrm{T}\) a prodloužení pružiny \(\Delta l = l - l_\mathrm{0} \).
Sestrojte graf \(\Vec{F}_\mathrm{T}\) v závislosti na \(\delta l \) a body proložte vhodnou křivku. O jakou matematickou závislost se jedná? Vyjádřete ji vzorcem.
Tuhost pružiny (značka \(k\), jednotka N/m) je definována jako síla, kterou bychom museli pružinu napínat, aby se prodloužila o jeden metr. Jaká je tuhost použité pružiny?