Mez pevnosti, prodloužení
Cvičení 1
Blok betonu o příčném průřezu 0,01 m2 se rozlomí, když na něj budeme tlačit silou 1 MN. Vypočítejte jeho mez pevnosti v tlaku. Jaké zatížení v kg blok snese?
Cvičení 2
Na následujícím obrázku jsou znázorněna namáhání různých materiálových vzorků. Vysvětlete, proč se vzorek B prodlouží více než vzorek A; proč se vzorek C prodlouží více než vzorek B; D více než C a E více než D.
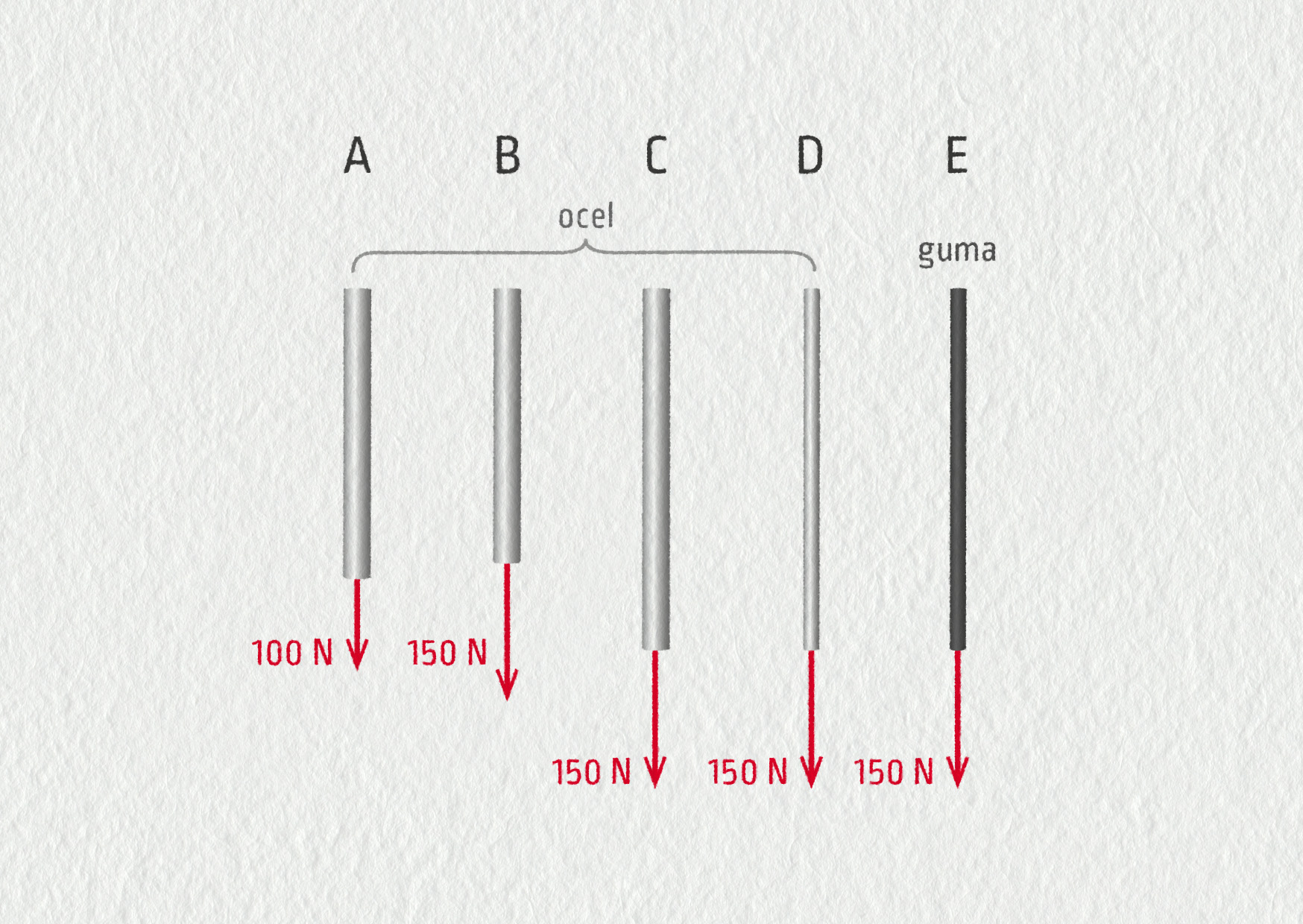
Zdroj
Cvičení 3
Mez pevnosti plexiskla je 87 MPa (viz tabulka). Z něj vyrobená tyč má příčný průřez 100 mm2. Co znamená termín „mez pevnosti“? Jak velkou tahovou silou bychom tyč přetrhli?
Cvičení 4
Ocel má mez pevnosti 520 MPa a modul pružnosti 204 GPa.
- Jakou silou můžeme maximálně zatížit drát z ní vyrobený, aby nedošlo k jeho přetržení, jestliže má průměr 1,1 mm?
- Jaké je v oceli napětí při zatížení drátu odpovídajícím síle 120 N?
- O kolik procent se při tomto zatížení drát prodlouží, předpokládáme-li, že stále platí Hookův zákon?
- 494 N
- 126 MPa
- 0,06 %
Cvičení 5
Gumové lano délky 4 m a průměru 50 mm volně visí v opičí kleci. Opice vážící 22 kg se pověsí na jeho konec. Jaká bude délka tohoto lana? Modul pružnosti gumy v tahu je 50 MPa.
Cvičení 6
Jak těžké závaží musíme zavěsit na ocelový drát o klidové délce 2,00 m a tloušťce 1 mm, aby se prodloužil o 1 mm? Modul pružnosti v tahu je pro danou ocel 220 GPa.
Cvičení 7
Měříme modul pružnosti gumové pásky. V oblasti lineární deformace byly naměřeny tyto hodnoty: síla \(F=0{,}5\ \mathrm{N}\pm1\,\%\), příčný průřez \(S=4\ \mathrm{mm}^2\pm3\,\%\), prodloužení \(\Delta l=(0{,}0080\pm0{,}0005)\ \mathrm{m}\) a původní délka \(l_0=(0{,}145\pm0{,}001)\ \mathrm{m}\). Vypočítejte modul pružnosti gumové pásky a odhadněte nejistotu provedeného měření.
Cvičení 8
Běžná pálená cihla má rozměry 29 cm × 14 cm × 6,5 cm a hmotnost 4 kg.
- Jaký tlak na podložku vyvolá, když leží na své největší straně?
- Jak vysokou zeď z těchto cihel bychom teoreticky mohli postavit, je-li její pevnost v tlaku 20 MPa?
- 966 Pa
- 1346 m
Cvičení 9
Jakou silou je napjata ocelová struna kytary o délce 0,65 m, obsahu průřezu 0,325 mm2, která se prodloužila o 5 mm?
Cvičení 10
Při našem objevování vesmíru je velmi limitujícím faktorem cena vynesení nákladu na oběžnou dráhu Země. Proto se konstruktéři zabývají myšlenkou kosmického výtahu, který by tyto práce velmi zlevnil. Problém při konstrukci vesmírného výtahu je ten, že nemáme k dispozici materiál, který by unesl svou vlastní váhu a ještě navíc užitečný náklad. Uvažujte lano zavěšené v tíhovém poli konstantní hodnoty.

Zdroj
Při překročení určité kritické délky se lano zavěšené v gravitačním poli přetrhne pouze svou vlastní tíhou. Vypočítejte tuto kritickou délku pro materiál, který si sami vyberete.
Poznámka: Další podrobnosti o kosmickém výtahu nalzenete například zde: https://web.archive.org/web/20160314170838/http://www.czechnationalteam.cz/?q=content%2Fvesmirny-vytah

