Od počátku se materiály vyvíjely metodou pokus-omyl, získávaly se zkušenosti, vylepšovaly se postupy. Dnes k vývoji materiálů používáme jak zkušební laboratoře, tak například počítačové modelování. Díky tomu můžeme vytvářet nové pokročilé materiály a znát přesně jejich vlastnosti.
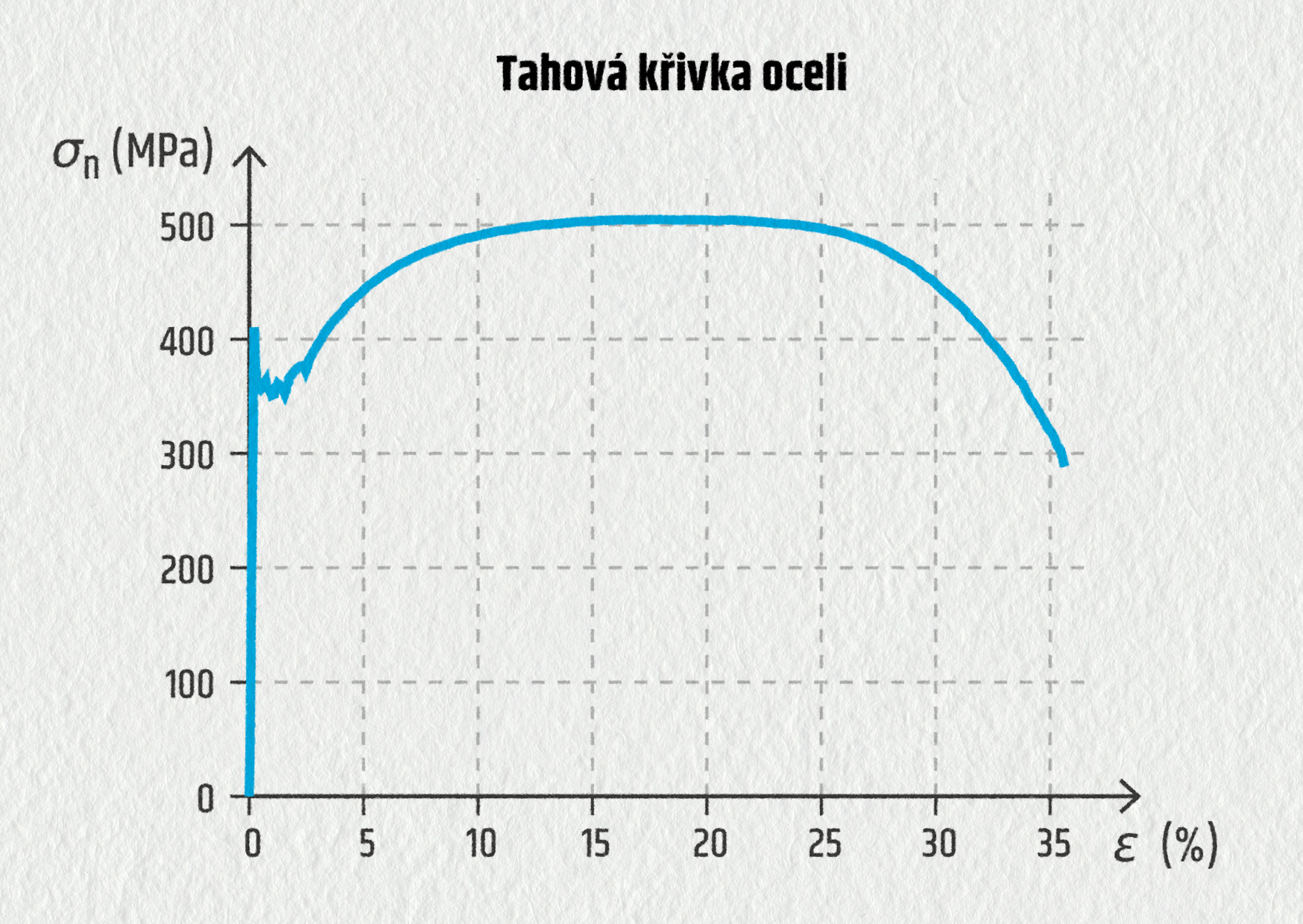
A jak dané materiály testujeme? Jedním z testů mechanických vlastností materiálu je deformační zkouška, při které materiál natahujeme nebo stlačujeme, popřípadě jinak deformujeme. Můžete si připomenout úvodní aktivitu č. 2. V tomto experimentu bylo trháno bavlněné vlákno krejčovské nitě. Z jeho výsledků můžeme usoudit, že toto vlákno vydrží poměrně velké namáhání, ale má také svou mez pevnosti. Při působení síly o velikosti kolem 10 N dojde k jeho přetržení (viz obrázek 13.5).
Tahová deformační zkouška je důležitou zkouškou pevnosti nejen bavlněných nití, ale především konstrukčních a stavebních materiálů. Vezmeme vzorek zkoumaného materiálu, upneme ho do trhacího stroje a postupně zvyšujeme sílu, kterou ho napínáme (viz schéma experimentu). Jestliže přitom měříme navíc prodloužení daného vzorku materiálu, můžeme vykreslit graf ukazující, jak deformace závisí na zatížení. Tato závislost se nazývá deformační křivka.
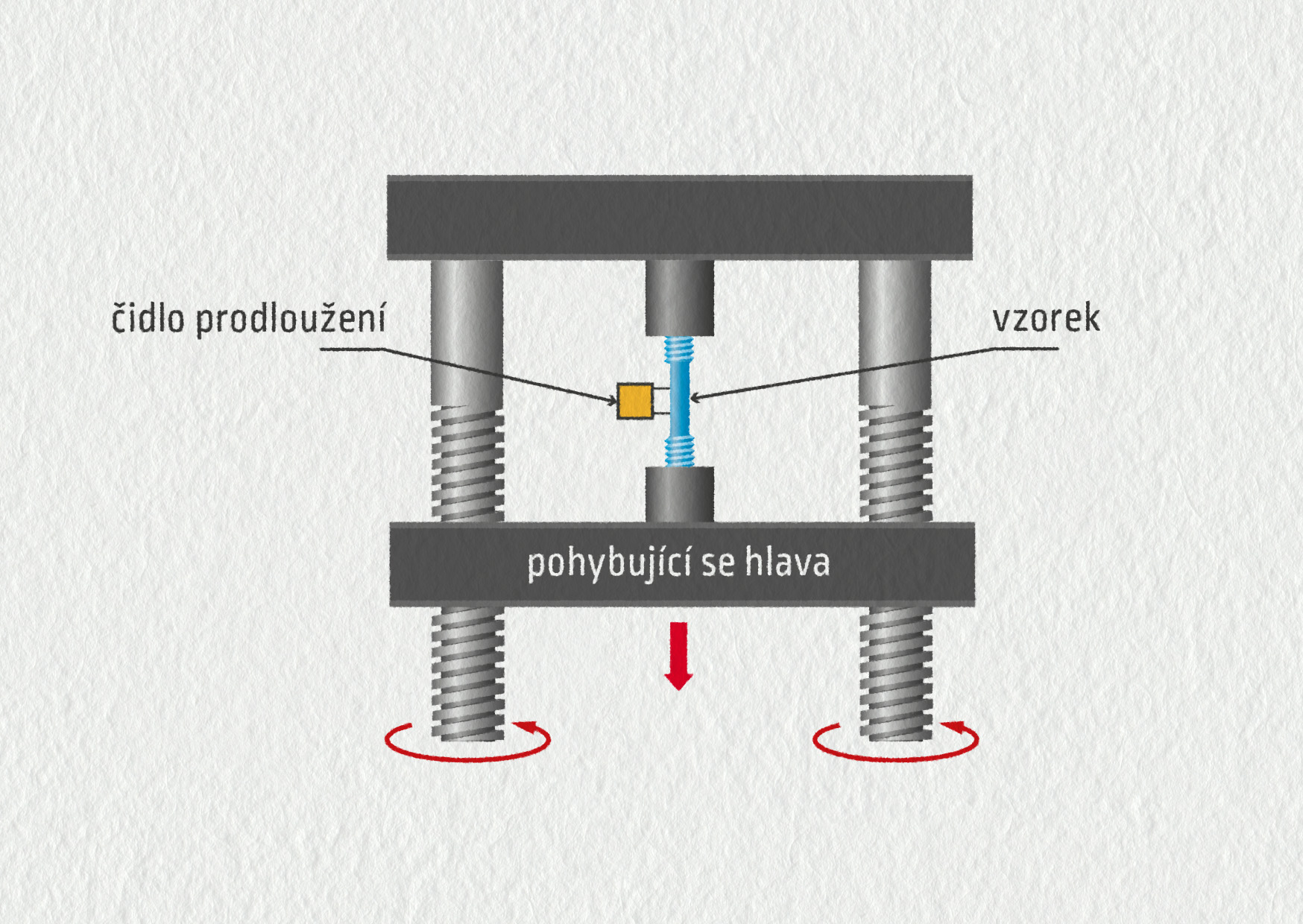
Zdroj
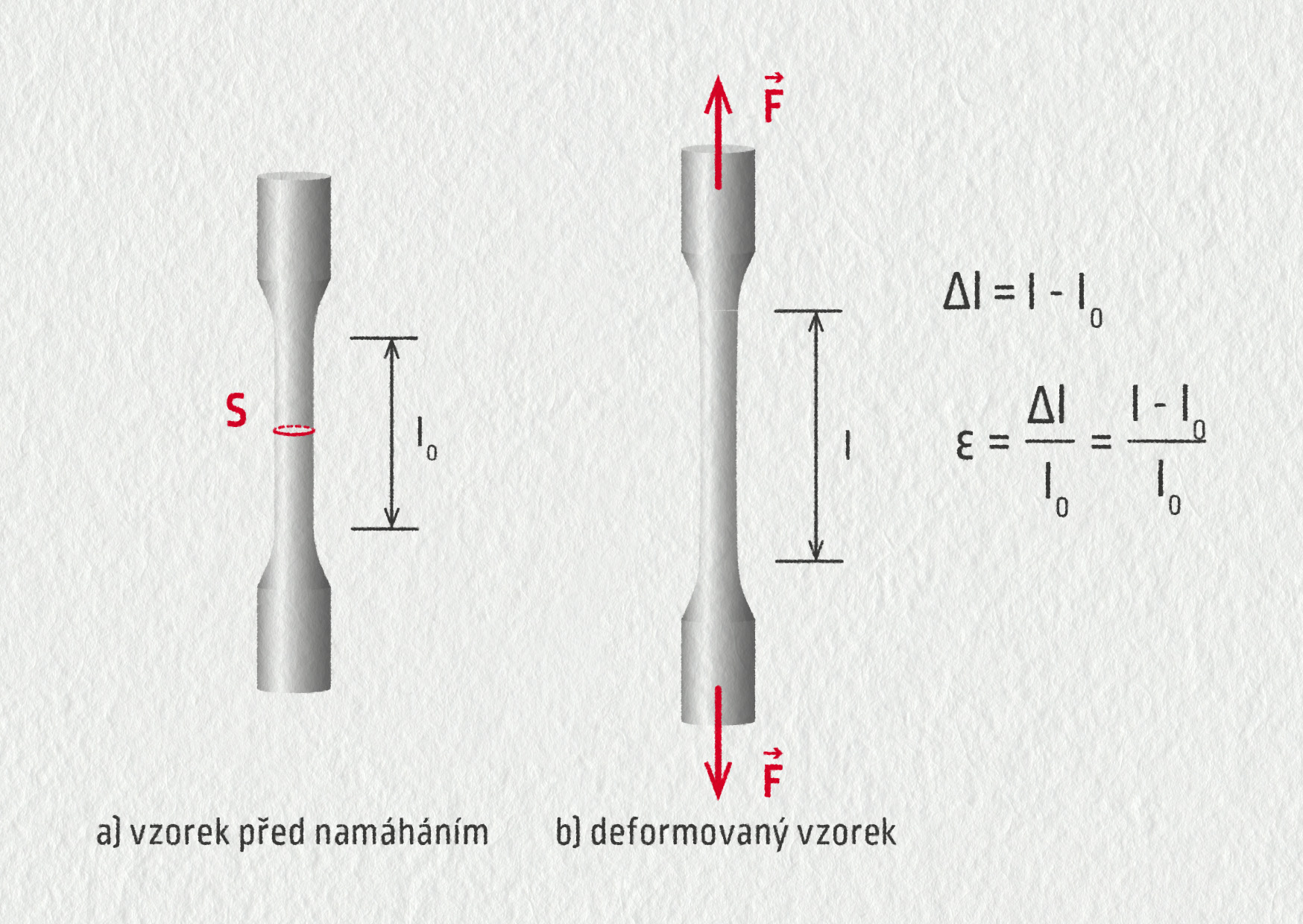
Abychom mohli porovnat dva materiály, musíme mít k dispozici buďto stejně dlouhé a stejně silné vzorky, nebo zavést veličiny, které budou charakterizovat daný materiál, a ne použitý zkoumaný vzorek. Takovými veličinami jsou normálové napětí \(\sigma_\mathrm{n}\) a relativní prodloužení \(\varepsilon\).
Normálové napětí \(\displaystyle \sigma_\mathrm{n} = \frac{F}{S} \)
\(F\) – velikost síly působící kolmo k průřezu o obsahu \(S\) daného vzorku
\(S\) – obsah příčného průřezu zkoumaného vzorku
Zdroj
Normálové napětí \(\sigma_\mathrm{n}=F/S\) je podíl deformační síly \(F\) a plochy \(S\), na kterou síla kolmo (normálově) působí. Vyjadřuje se v Pa, běžné konstrukční materiály mají pevnost ve stovkách MPa.
Relativní prodloužení \(\displaystyle \varepsilon=\frac{\Delta l}{l_0} \)
\(\Delta l=l-l_0\) – prodloužení vzorku
\(l\) – délka vzorku při namáhání
\(l_0\)– délka v nenapjatém stavu
Zdroj
Relativní prodloužení zase ukazuje, o kolik se materiál prodlouží vzhledem ke své původní délce \(\varepsilon=\Delta l/l_0\). Je to veličina bezrozměrná, někdy ji vyjadřujeme v procentech.
Kontrolní otázka
Kontrolní otázka
Zdroj
Zdroj
V grafu deformační křivky znázorňujeme normálové napětí \(\sigma_\mathrm{n}\) v závislosti na relativním prodloužení \(\varepsilon\).
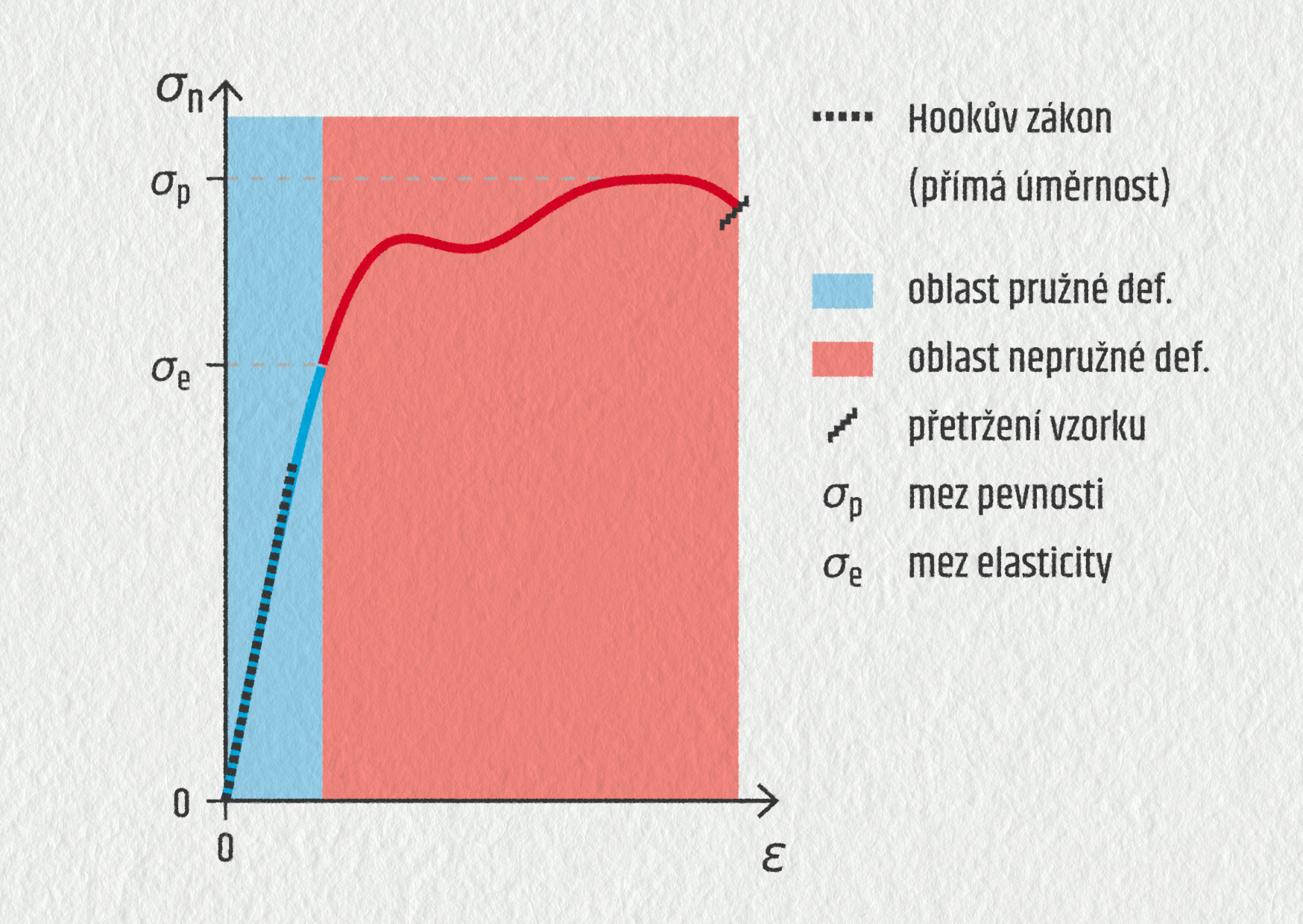
Nejprve se vzorek chová pružně. To znamená, že když vzorek materiálu namáháme silou nebo napětím a následně zatěžující sílu odstraníme (materiál odlehčíme), vrátí se vzorek do původní délky \(l_0\). Zkuste trochu natáhnout pružinku z propisovací tužky. Po odlehčení se vrátí na původní délku. Deformace je elastická. Kdybyste ale natáhli pružinku více, už by se po odlehčení do původní délky nevrátila, ale zůstala by zčásti trvale deformovaná. Taková deformace je plastická, trvalá.
V grafu deformační křivky elastické deformaci přibližně odpovídá lineární část grafu, plastické zbylá část až do bodu přetržení.
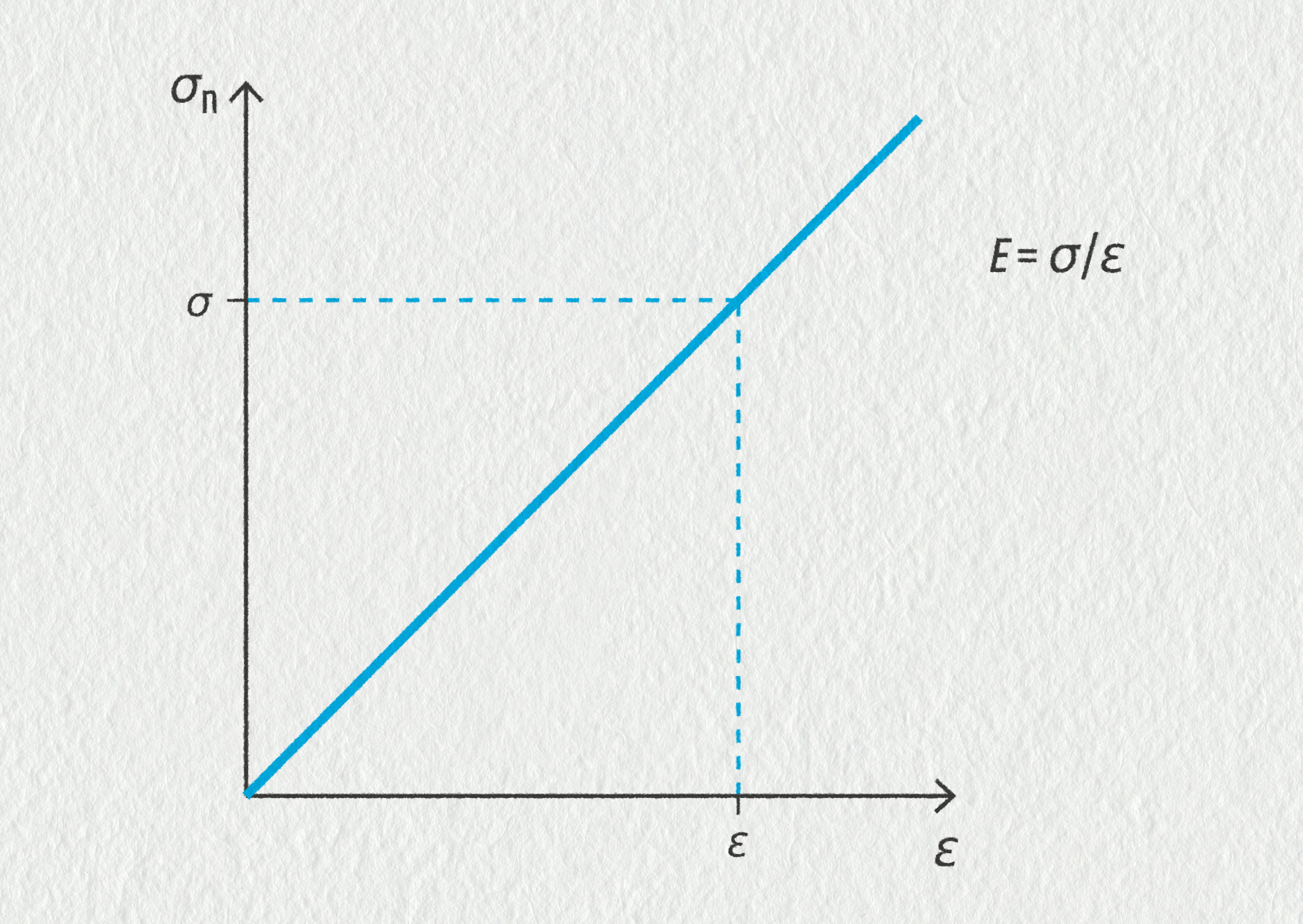
Zdroj
V oblasti elastické deformace je normálové napětí přímo úměrné relativnímu prodloužení.
V grafu vidíme přímku procházející počátkem. Tato závislost je matematicky popsána Hookovým zákonem \(\sigma_\mathrm{n}=E\varepsilon\). Konstanta úměrnosti \(E\) je Youngův modul pružnosti, který vyjadřuje strmost křivky, a tedy tuhost materiálu, o níž ještě bude řeč později. Jeho hodnota je velká pro materiály s vysokou tuhostí, které se málo deformují i při vysokých zátěžných silách. Youngův modul vyjadřujeme v Pa, ale v praxi se setkáme spíše s jeho násobky: MPa, GPa (např. pro ocel platí \(E=200\ \mathrm{GPa}\)). Hookův zákon je rovnicí přímky, popisuje tedy pouze lineární část deformační křivky.
Poznámka na okraj: Inženýrské napětí
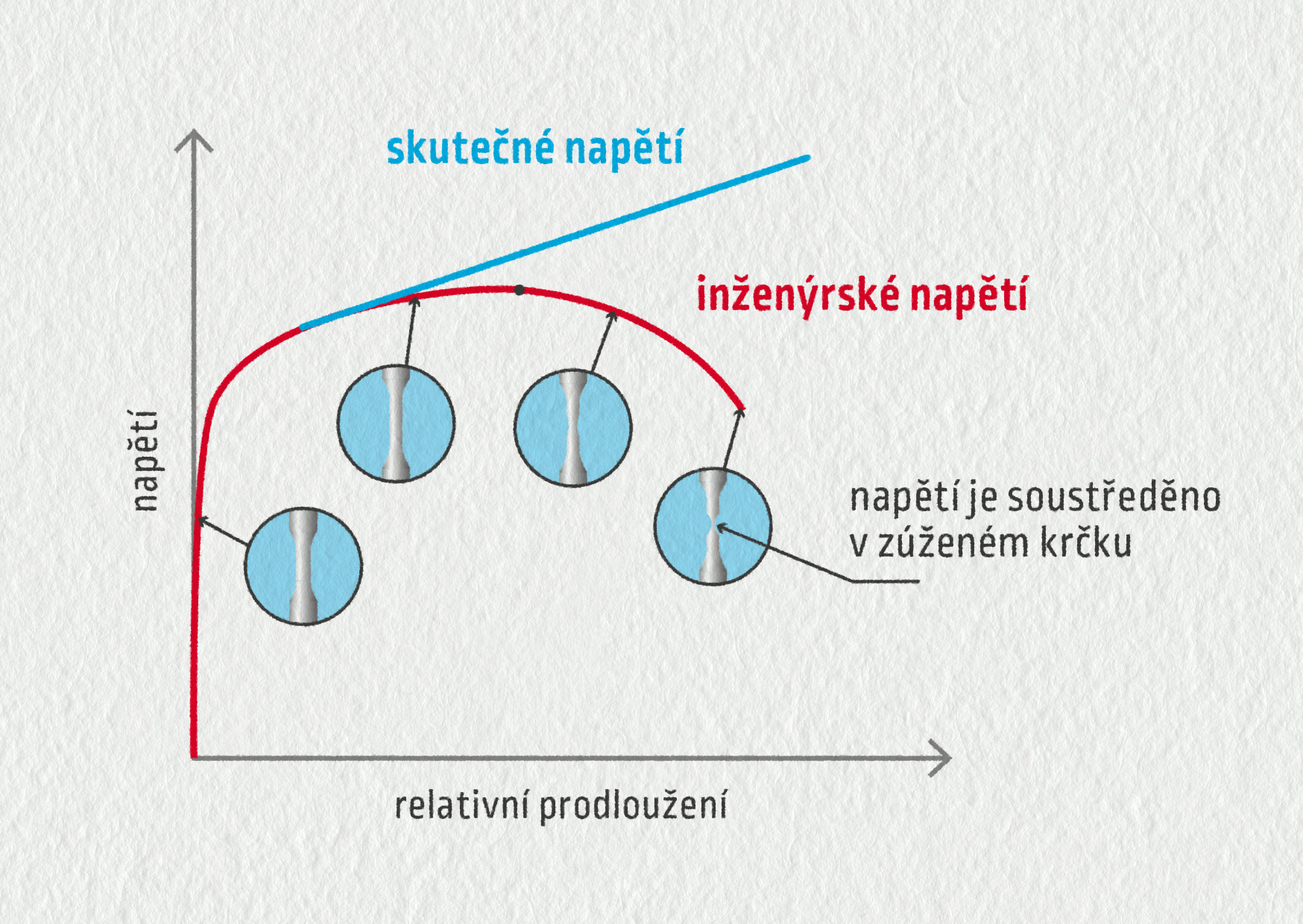
Možná se divíte, že deformační křivka ve svém závěru klesá. Zde je vysvětlení: v typickém kovovém materiálu dochází od určité chvíle k jevu, který nazýváme tečení materiálu. Od tohoto okamžiku se již nezvyšuje působící síla, dokonce dochází k jejímu poklesu, a proto je křivka v této části klesající. Někdy bývá v literatuře uváděno tzv. skutečné napětí. To je definováno jako síla působící na skutečný průřez zkoušeného materiálu. a protože se zkoumaný vzorek při natahování zužuje (vznik krčku), skutečný příčný průřez je menší, a skutečné napětí tak nabývá větších hodnot, deformační křivka roste až do přetržení.
V technické praxi pracujeme s inženýrským napětím a stejně tomu je tak i v této učebnici.
Zdroj
Poznámka na okraj: Jednoduchý model elastické deformace
Pevné těleso si můžeme představit jako malé kuličky (atomy) spojené malými pružinkami (znázorňujícími meziatomární síly). Budeme-li takovou pevnou tyč tahat za její konec silou \(F\), každá z pružinek se prodlouží ve směru síly o stejně malý kousek, a celkové prodloužení \(\Delta l\) tak bude přímo úměrné síle \(F\). Píšeme \(\Delta l\propto F\).
Toto prodloužení \(\Delta l\) je také přímo úměrné původní délce tyče l0. Proč? Jestliže se meziatomární pružinky prodlužují zcela stejně, v delší tyči bude atomů (a také pružinek mezi nimi) větší počet, a celkově se tedy tyč musí více prodloužit. Máme tedy \(\Delta l\propto l_0\).
Nakonec ještě uvažme, že napětí pro danou sílu \(F\) je nepřímo úměrné obsahu příčného průřezu tyče \(S\) (viz definice). Prodloužení \(\varepsilon\) je tedy také nepřímo úměrné obsahu \(S\). Celkově tedy máme
\( \Delta l \propto \frac{Fl_0}{S} \) nebo také \( \Delta l=k\frac{Fl_0}{S}\;. \)
Vydělíme-li rovnici \(l_0\), získáme vztah
\[ \frac{\Delta l}{l_0} = k\frac{F}{S}\;, \]který můžeme také přepsat do tvaru
\[ \frac{F}{S} = \frac{1}{k} \frac{\Delta l}{l_0} \]neboli je tu nám již známý Hookův zákon ve tvaru \(\sigma_\mathrm{n}=E\varepsilon\).
| Látka | E (GPa) | Mez pevnosti (MPa) |
|---|---|---|
| Al | 70,7 | 45 |
| Cu | 123 | 200 |
| Ag | 79 | 170 |
| Au | 78,5 | 100 |
| Fe α | 212 | 262 |
| diamant | 1 050 | – |
| dural | 76 | 450 |
| litina | 110 | 414 |
| mosaz | 110 | 315 |
| běžná ocel (do 0,25 % uhlíku) | 200 | 400–550 |
| nástrojářská ocel (0,5–1,5 % uhlíku) | 200 | 1860 |
| SiO2 | 73 | 48 |
| kaučuk | 0,05 | 5 |
| sklo | 80 | 60 |
| plexisklo | 3,3 | 87 |
| beton | 60 | 2 |
| kevlar | 130 | 3600 |
Poznámka: Pro některé materiály jsou hodnoty pevnosti v tlaku nebo v tahu přibližně stejné, pro jiné naopak velmi rozdílné.
Porovnejme nyní různé materiály z hlediska jejich pevnosti a pružnosti:
Zdroj
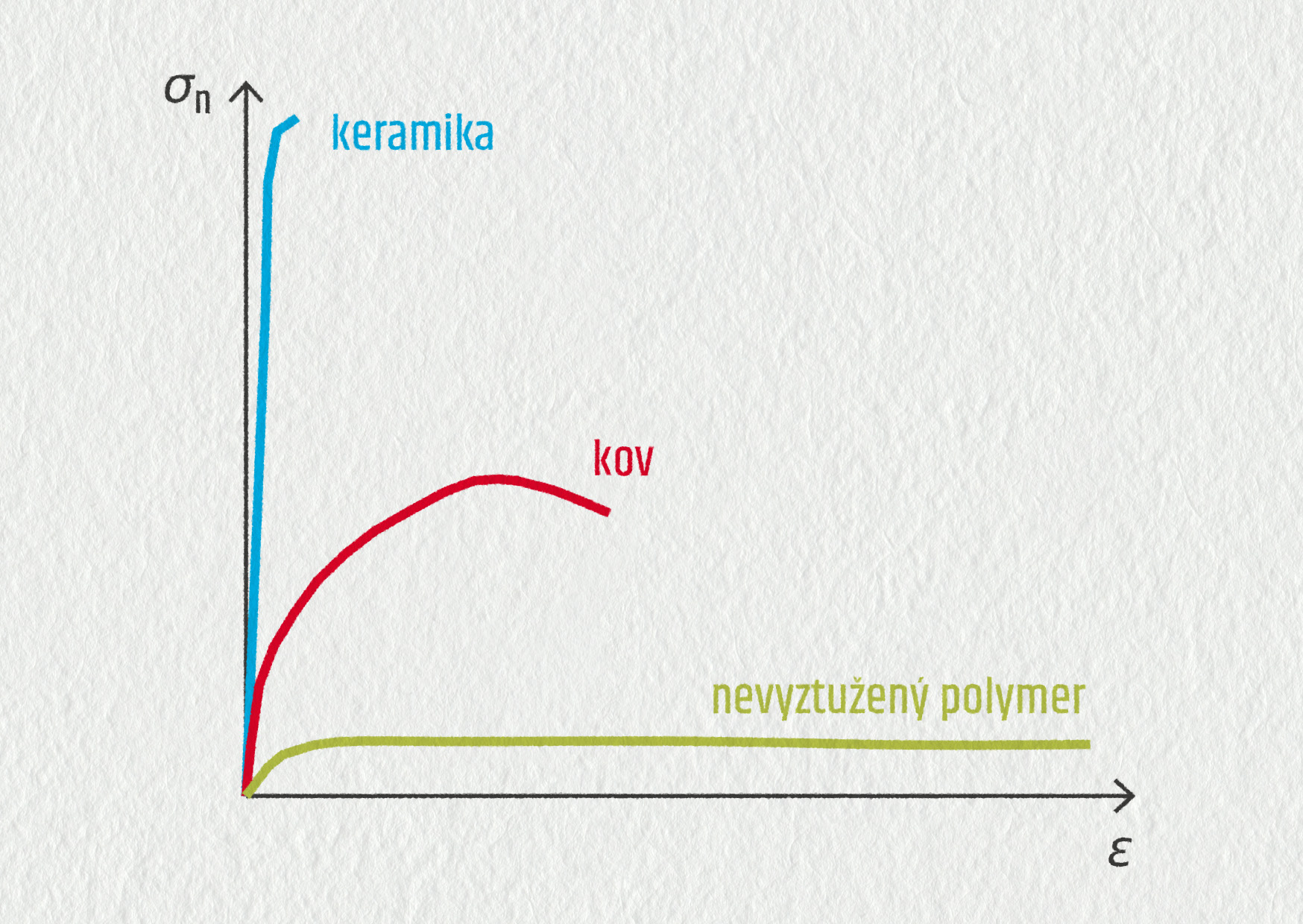
Tři různé deformační tahové křivky na obrázku ukazují tři velmi odlišné materiály – keramiku, kovy a nevyztužené polymery (plasty nebo gumy). Všechny křivky ukazují, že v oblasti elastické deformace napětí roste při prodlužování vzorku. Toto napětí ale roste různě strmě, dosáhne různé nejvyšší hodnoty napětí a různého největšího relativního prodloužení. Konec křivky signalizuje okamžik přetržení vzorku materiálu.
Modrá křivka ukazuje keramiku, která má z těchto tří materiálů nejvyšší tuhost (velká síla způsobí pouze malou deformaci, to odpovídá velkému modulu pružnosti). Současně má nejvyšší pevnost (při přetržení vzorku bylo dosaženo největšího napětí) a nakonec vykazuje nejmenší tažnost (nejmenší relativní prodloužení při přetržení). Takové vlastnosti mají všechny křehké materiály.
Druhým extrémem je křivka zelená, která odpovídá chování některých polymerů (PVC, PET a další). Pevnost (největší dosažená síla) i tuhost (strmost nárůstu síly vzhledem k prodloužení) jsou ve srovnání s keramikou a kovy velmi nízké. Naopak polymery vykazují vysokou tažnost. Je vidět, že relativní prodloužení dokonce roste bez výrazného nárůstu zatěžovacího napětí. Tyto materiály nazýváme elastické.
Tahová křivka kovových materiálů (červená) leží mezi těmito dvěma extrémy. Kovy mají relativně vysokou pevnost, tuhost i tažnost.
Kontrolní otázka
Kontrolní otázka
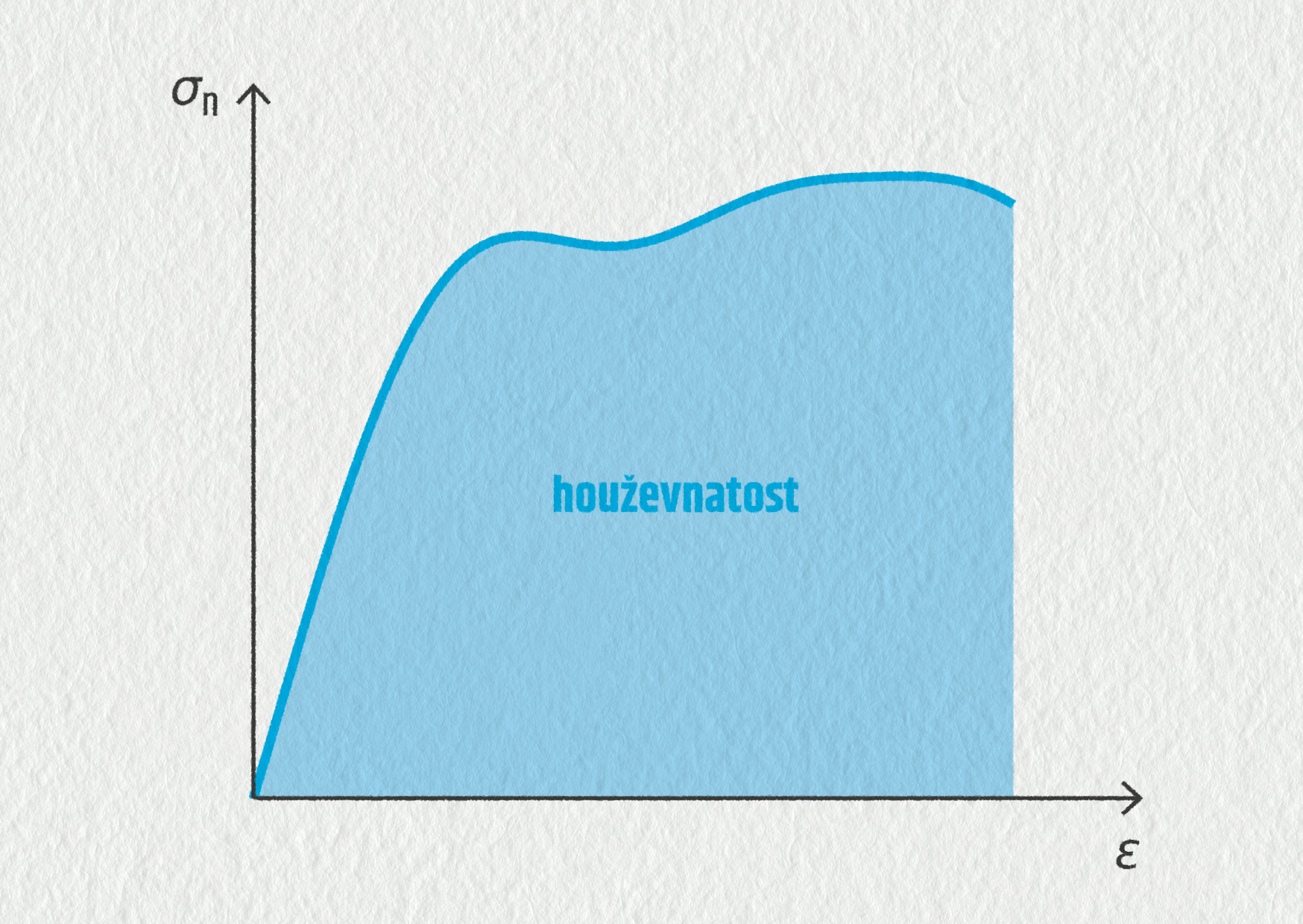
Při pohledu na deformační křivku můžeme ještě mluvit o houževnatosti. Houževnatost
v sobě zahrnuje jak pevnost, tak tažnost a je vyjádřena plochou pod tahovou křivkou. Tato plocha vyjadřuje deformační energii na jednotku objemu nutnou pro porušení materiálu.
Zdroj
Nejjednodušeji bychom mohli říct, že houževnatost vyjadřuje odolnost materiálu proti vzniku porušení. Je vidět (viz obrázek 13.37), že z hlediska houževnatosti jsou na tom nejlépe kovy. Keramiky mají sice největší pevnost, ale malou tažnost (jsou křehké), mají tedy malou houževnatost. Polymery sice vydrží velké deformace, ale nejsou schopny unést velkou sílu. Jejich houževnatost je opět velmi malá.
Podle hodnot pevnosti, tuhosti, tažnosti a houževnatosti, ale i dalších vlastností, které jsme zatím nezmínili, se různé materiály hodí pro různé účely.
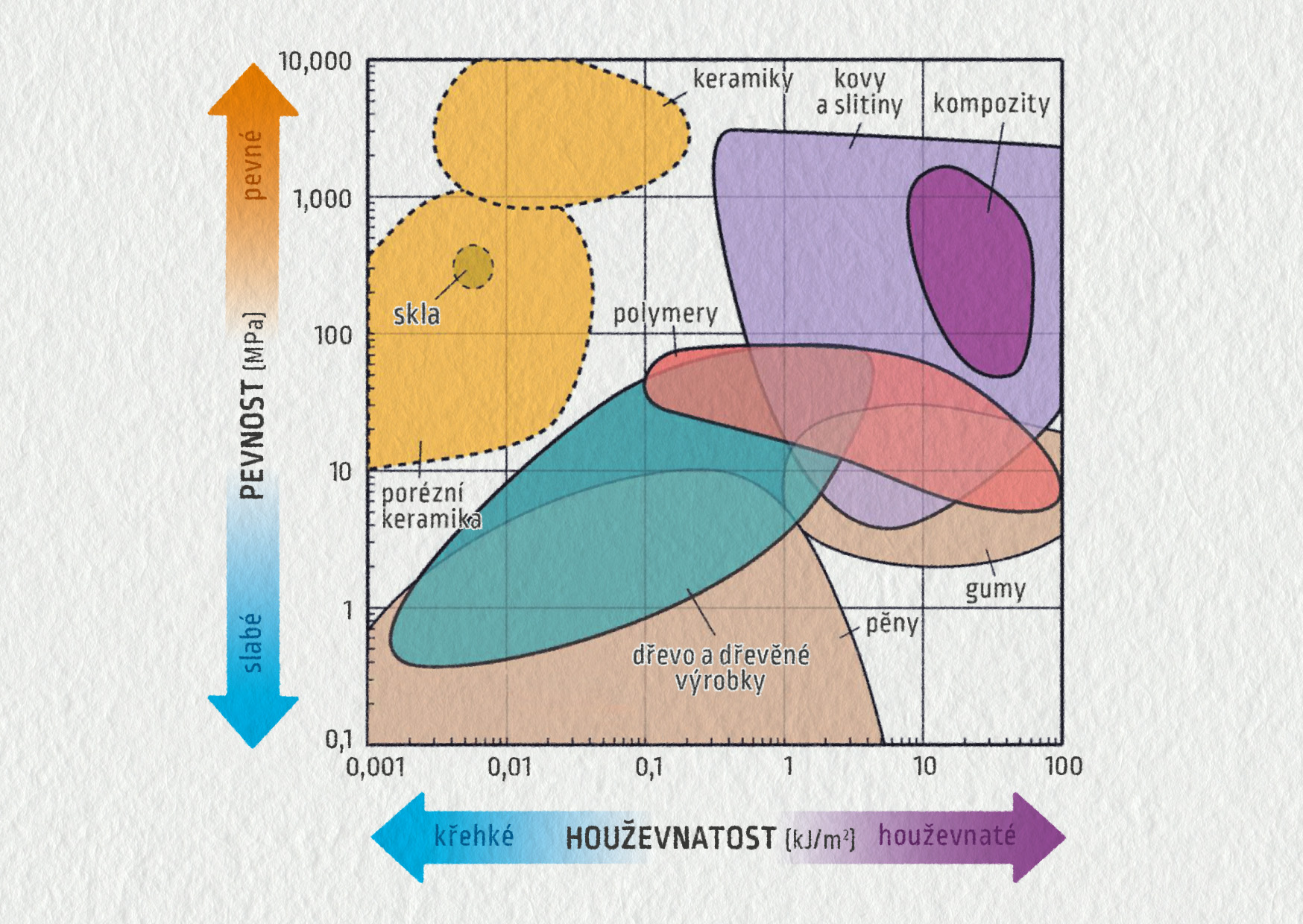
Zdroj
Zdroj a podrobnější rozdělení: http://www-materials.eng.cam.ac.uk/mpsite/interactive_charts/strength-toughness/basic.html
Poznámka – Keramika: V grafu je ukázána pevnost v tlaku, tahová pevnost keramiky je obvykle 10 % tlakové. Ostatní materiály: Pevnost v tahu/tlaku
Kontrolní otázka
Kontrolní otázka
Kontrolní otázka
Kontrolní otázka
Kontrolní otázka
Fakt, zda je materiál pevný či křehký, jak moc je elastický nebo zda je houževnatý, tedy určuje, v jaké oblasti jej použijeme. Tyto vlastnosti musíme změřit. a pak je také nutno přesně znát napětí, která v mostech, tričkách nebo převodovkách vznikají. Vybraný materiál pak musí zároveň zatížení vydržet, ale celá konstrukce nesmí být příliš masivní. Po mostě budou jezdit jen auta a nikoli vlaky a tanky, převodovka by neměla mít 300 kg, to pak roste spotřeba materiálu nebo spotřeba pohonných hmot.
Vidíme, že výběr materiálu není tak jednoduchý! Někdy je to pěkná materiálová věda.
