Rozsah velikostí ve vesmíru je obrovský – od atomového jádra (0,000 000 000 000 001 m) po mezigalaktické vzdálenosti (1 000 000 000 000 000 000 000 m). K zápisu takových čísel potřebujeme lepší způsob než hromadu nul. Jednou z možností je použít vědecký zápis čísla pomocí mocnin deseti. Zápis vypadá takto:
Vědecký zápis čísla: a · 10n. Například:
150 · 106 km = 150 · 1 000 000 km = 150 000 000 km
12 · 10−5 m = 12 · 0,000 01 m = 0,000 12 m
Číslo n (říká se mu exponent) může být z množiny celých čísel, tedy 1, 2, 3, … pro zápis velkých čísel (101 = 10, 102 = 100, 103 = 100, …) a −1, −2, −3, … pro zápis malých čísel (10−1 = 0,1, 10−2 = 0,01, 10−3 = 0,001, …).
Zvyšováním exponentu můžeme posouvat desetinnou čárku doleva a naopak:
150 · 106 km = 15 · 107 km = 1,5 · 108 km nebo 12 · 10−5 m = 1,2 · 10−4 m
Pomocí vědeckého zápisu můžeme rovněž převádět jednotky, například:
150 · 106 km = 150 · 109 m nebo 1,2 · 10−4 m = 0,12 · 10−3 m = 0,12 mm.
Použití předpon je druhou možností zápisu velkých a malých čísel. Nejčastěji se ve fyzice používají následující předpony:
| Název | Hodnota | Symbol | |
|---|---|---|---|
| kilo | 103 | 1 000 | k |
| mega | 106 | 1 000 000 | M |
| giga | 109 | 1 000 000 000 | G |
| tera | 1012 | 1 000 000 000 000 | T |
| Název | Hodnota | Symbol | |
|---|---|---|---|
| mili | 10-3 | 0,001 | m |
| mikro | 10-6 | 0,000 001 | μ |
| nano | 10-9 | 0,000 000 001 | n |
| piko | 10-12 | 0,000 000 000 001 | p |
Pro hodnoty mezi tisícinou a tisícem ještě používáme tyto předpony:
| Název | Hodnota | Symbol |
|---|---|---|
| hekto | 102 | h |
| deka | 101 | dag |
| deci | 10−1 | d |
| centi | 10−2 | c |
Zapište následující čísla pomocí vědeckého zápisu a poté s využitím vhodné předpony:
- 1 světelný rok = 9 460 000 000 000 km =
- řádová velikost atomu = 0,000 000 000 1 m =
- 9 460 000 000 000 km = 9,46 ⋅ 1012 km = 9,46 ⋅ 1015 m = 9 460 Tm
- 0,000 000 000 1 m = 10–10 m = 0,1 nm
Proč vlastně vědecký zápis používat? Má to několik výhod. Nemusíme psát mnoho nul. Můžeme snadněji porovnávat různé velikosti – podíváme se pouze na mocninu deseti a máme jasno. Kromě toho se s těmito čísly dá dobře počítat. Vše si ukážeme v úlohách.
Vyjádříme-li oba rozměry v mocninách deseti, dostaneme:
- Velikost atomu: 0,1 nm = 1,0 · 10−10 m.
- Velikost bakterie: 10 µm = 1,0 · 10−5 m.
Exponent deseti se liší o 5, proto řekneme, že bakterie je o 5 řádů větší než atom, což znamená 105krát větší neboli 100 000krát větší.
Podle gravitačního zákona se každé dva hmotné body navzájem přitahují silou, jejíž velikost můžeme vyjádřit vztahem \[ F_\mathrm{g} = G\,\frac{m_1 m_2}{r^2} \] Tělesa mají hmotnosti m1 a m2, jsou od sebe vzdálená r a konstanta přímé úměrnosti je tzv. gravitační konstanta \(G = 6{,}67\cdot10^{-11}\ \mathrm{N\ m^2\ kg^{-2}}\).
- Určete řádově (přibližně, bez použití kalkulačky) velikost síly, kterou se přitahují dva lidé o hmotnosti 70 kg ve vzdálenosti 2 m.
- Určete velikost síly přesně s pomocí kalkulačky (použijte tlačítko EXP nebo ×10n)
- \[F_\mathrm{g} = G\frac{m_1m_2}{r^2} = 7\cdot10^{-11}\cdot70\cdot70/2^2\ \mathrm{N} \approx 10^{-7}\ \mathrm{N}\]
- \[F_\mathrm{g} = G\frac{m_1m_2}{r^2} = 8\cdot10^{-8}\ \mathrm{N}\]
Jak správně převádět jednotky?
Základní pravidla pro převody jednotek jistě znáte. Připomeneme zde ty nejdůležitější s využitím vědeckého zápisu tam, kde je to vhodné.
| 1 540 200 0,009 3 6,02 ⋅ 1023 |
Velká čísla zapisujeme s mezerami po třech řádech od konce čísla. Malá čísla zapisujeme s mezerami po třech řádech od desetinné čárky. Pro velmi malá a velmi velká čísla používáme vědecký zápis. |
| 2,4 mm = = 2,4 ⋅ 0,001 m = = 0,002 4 m 2,4 mm = 0,002 4 m |
Při převodu vyjádříme původní jednotku pomocí požadované a poté provedeme násobení. Případně rovnou posuneme desetinnou čárku. |
| 5,6·105 m = = 5,6·105 ·10-3 km = = 5,6 ⋅ 102 km 5,6 ⋅ 105 m = 5,6 ⋅ 102 km |
Při převodu vyjádříme původní jednotku pomocí požadované a poté provedeme násobení. Případně rovnou změníme exponent. |
| 3 m2 = = 3 ⋅ (100 cm)2 = = 3 ⋅ 10 000 cm2 = = 30 000 cm2 3 m2 = 30 000 cm2 |
Při převodu čtverečních a krychlových jednotek vyjádříme původní jednotku pomocí požadované a poté umocníme a vynásobíme. Případně rovnou posuneme desetinnou čárku. |
| 9,4 km3 = 9,4 ⋅ (103 m)3 = 9,4 ⋅ 109 m3 9,4 km3 = 9,4 ⋅ 109 m3 |
Při převodu čtverečních a krychlových jednotek vyjádříme původní jednotku pomocí požadované a poté umocníme. Případně rovnou změníme exponent. |
Co je to logaritmické měřítko?
Vzhledem k tomu, že tělesa a vzdálenosti kolem nás jsou co do velikosti velmi různé, není jednoduché tyto velikosti znázornit na číselné ose. Musíme si pomoci zvláštním měřítkem, kterému se říká logaritmické (název pochází od matematické funkce logaritmus, jejíž přesná definice ale pro tuto chvíli není potřeba). Logaritmické měřítko je určeno tak, že jeden dílek na číselné ose představuje desetinásobný skok. Jestliže se tedy díváte na dílek označený 1, sousední vpravo bude již 101, další 102 a tak dále. Směrem doleva budou dílky označeny 10−1, 10−2 atd.
Co dílek na ose, to 10× větší nebo menší rozměr. Dílky jednoduše odpovídají mocninám deseti. Na několika centimetrech pak můžeme znázornit velikosti objektů z celého viditelného vesmíru.
| atom | 0,1 nm |
| virus | 100 nm |
| tloušťka vlasu | 0,1 mm |
| člověk | 1 m |
| Země | 10 000 km |
Do tabulky jsme doplnili i některé další objekty.
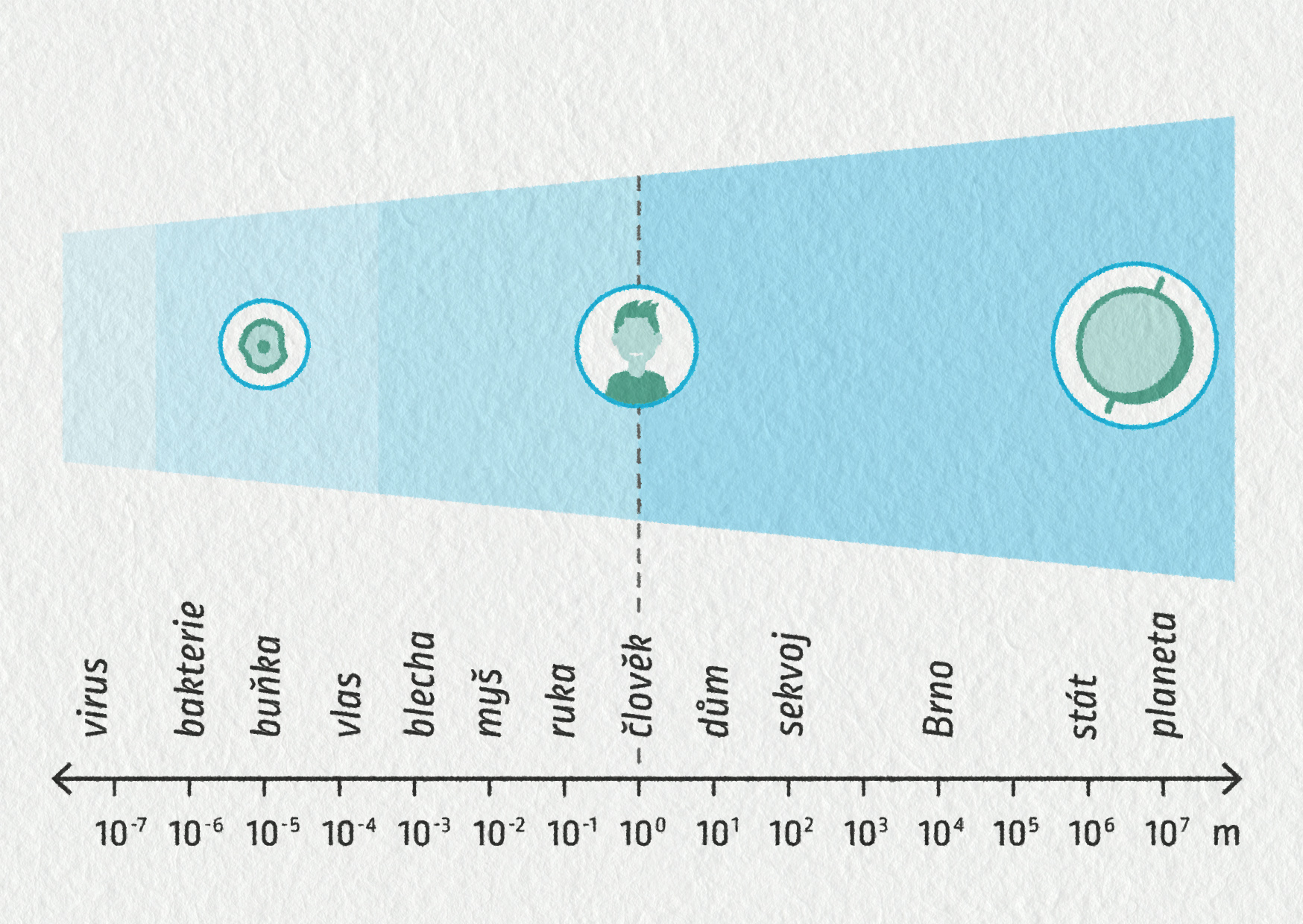
Zdroj
Rozměry nám dostupného světa tedy dosahují rozměrů zhruba od 10−15 m (velikost jádra atomu) až po 1026 m (13 miliard světelných let k nejvzdálenějším galaxiím). Zabírají tedy celkem 41 řádů! Na tomto obrovském rozpětí délek jsou však značné „mezery“. Například mezi 10−15 m (rozměr atomového jádra) a 10−10 m (rozměr celého atomu). Nebo například Slunce je od Země vzdáleno přibližně 1011 m a další nejbližší hvězda (Proxima Centauri) je vzdálená 1016 m. Mezi těmito hvězdami pak najdeme pouze prázdný prostor. Struktura vesmíru je tedy značně děravá, stejně jako struktury hmoty na nejjemnějším měřítku.

