Stavová rovnice
Cvičení 1
- Popište slovy, jak souvisí tlak plynu s chaotickým pohybem částic.
- Množství plynu můžeme popsat pomocí látkového množství \(n\), počtu částic \(N\) nebo hmotnosti \(m\). Jak spolu tyto veličiny souvisí?
- V naftovém motoru dochází k samovznícení směsi ve válci. Vysvětlete, jak je toho dosaženo.
- Do jaké hloubky se musí potopit potápěč, aby objem vzduchu v jeho plicích klesl na polovinu? Změní se přitom v jeho plicích množství plynu?
- Při stlačování pístu injekční stříkačky poměrně přesně platí, že tlak v pístu je nepřímo úměrný objemu plynu. Co z toho vyplývá pro teplotu plynu v pístu?
- Je pravda, že pokud ohřejeme plyn v pevné nádobě ze 100 °C na 200 °C, vzroste tlak na dvojnásobek? Vysvětlete.
- Potápěč si odpoledne připravil tlakovou láhev s plynem NITROX, manometr ukazoval tlak 9 kPa. Ráno si láhev přišel vyzvednou a manometr už ukazoval jen 8,5 kPa. Znamená to, že láhev uniká? Vysvětlete.
Cvičení 2
Nejhlubší vakuum, kterého lze dosáhnout v laboratoři, odpovídá zhruba tlaku 10−10 Pa. Kolik molekul připadá na 1 dm3 plynu o teplotě 0 °C za takto nízkého tlaku? V meziplanetárním prostoru Sluneční soustavy se tlak pohybuje okolo 10−15 Pa. Kolik částic najdeme v 1 litru v tomto případě?
asi 26 000 000, asi 260
Cvičení 3
Vzduchoplavecký balón naplněný heliem vystoupil z místa, kde byla teplota 290 K a tlak 98,5 kPa, do výšky, kde byla teplota 260 K a tlak 86,5 kPa. Jak velký byl objem balonu ve výšce, jestliže na počátku byl jeho objem 950 m3?
970 m3
Cvičení 4
Na obrázku vidíte 3 grafy zobrazující měření závislosti tlaku daného množství plynu na objemu či teplotě. Při jednom pokusu zůstával konstantní objem (\(V=\mathrm{konst}.\)), při druhém byla stálá teplota (\(T=\mathrm{konst}.\)) a při třetím stálý tlak (\(p=\mathrm{konst}.\)). Přiřaďte k pokusům správné grafy.
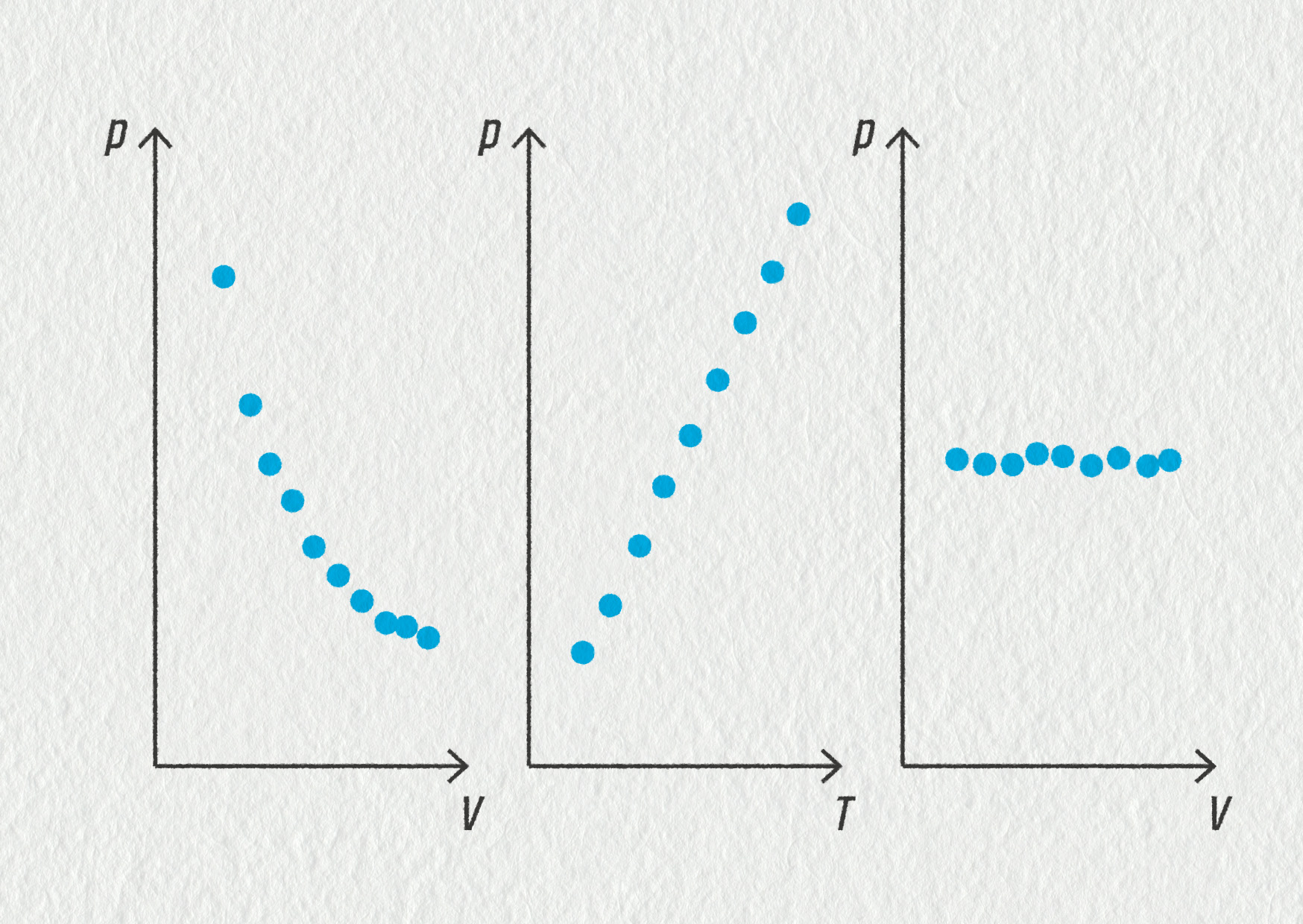
Zdroj
Cvičení 5
V tlakové nádobě o objemu 0,75 l je při teplotě 25 °C tlak 3,6 atmosféry. Nádoba podle výrobce odolá max. tlaku 10 atmosfér. Jaká je maximální možná teplota nádoby?
560 °C
Cvičení 6
Určete, o kolik procent klesne tlak v automobilové pneumatice, pokud se vnější teplota sníží z 20 °C na −15 °C. Objem pneumatiky se přitom nemění.
o 12 %
Cvičení 7
Pomocí zahřívání plynu v uzavřené nádobě můžeme určit teplotu absolutní nuly. Při laboratorním experimentu bylo změřeno, že při teplotě 20 °C má dusík objem 0,22 m3 a při teplotě 167 °C se rozepne na 0,33 m3. Výsledky zaneste do grafu a určete teplotu absolutní nuly.
−274 °C
Cvičení 8
Pomocí stavové rovnice ideálního plynu odvoďte, že pro absolutní vlhkost vzduchu platí \(\displaystyle\Phi=\frac{pM_\mathrm{m}}{RT}\). Uvažte, že \(\Phi\) není nic jiného než hustota vodní páry ve vzduchu.
Cvičení 9
Hustota vzduchu při teplotě 0 °C a tlaku 100 kPa je 1,275 kg ⋅ m−3.
- Jaká bude hustota vzduchu při tlaku 100 kPa a teplotě 20 °C?
- Jaká bude hustota vzduchu při tlaku 100 kPa a teplotě −20 °C?
- 1,188 kg ⋅ m−3;
- 1,376 kg ⋅ m−3
Cvičení 10
Vypočítejte hustotu argonu při teplotě 20 °C za atmosférického tlaku. Použijte stavovou rovnici.
1,66 kg/m3
Cvičení 11
- Pomocí vztahu pro průměrnou kinetickou energii jedné molekuly ideálního plynu odvoďte vzorec pro střední kvadratickou rychlost \(v_\mathrm{K}=\sqrt{3kT/m_0}\).
- Pomocí vzorce vypočítejte střední kvadratickou rychlost molekul kyslíku a vodíku při teplotě 0 °C.
b) kyslík 460 m/s, vodík 1850 m/s. Rychlosti jsou opravdu velké, a velká je tedy i energie uložená v chaotickém pohybu molekul.

