Pohyb po kružnici

Těleso se pohybuje po kružnici s poloměrem 50 cm rychlostí 2 m/s. Vypočítejte

1. periodu a frekvenci pohybu,
2. úhlovou rychlost,
3. kolik oběhů vykoná za 1 minutu,
4. dostředivé zrychlení tělesa.

Země obíhá kolem Slunce po přibližně kruhové trajektorii o poloměru 150 milionů km (= astronomická jednotka = 1 AU). Určete

1. periodu a frekvenci pohybu,
2. úhlovou rychlost,
3. rychlost pohybu Země,
4. s jakým dostředivým zrychlením se Země pohybuje.

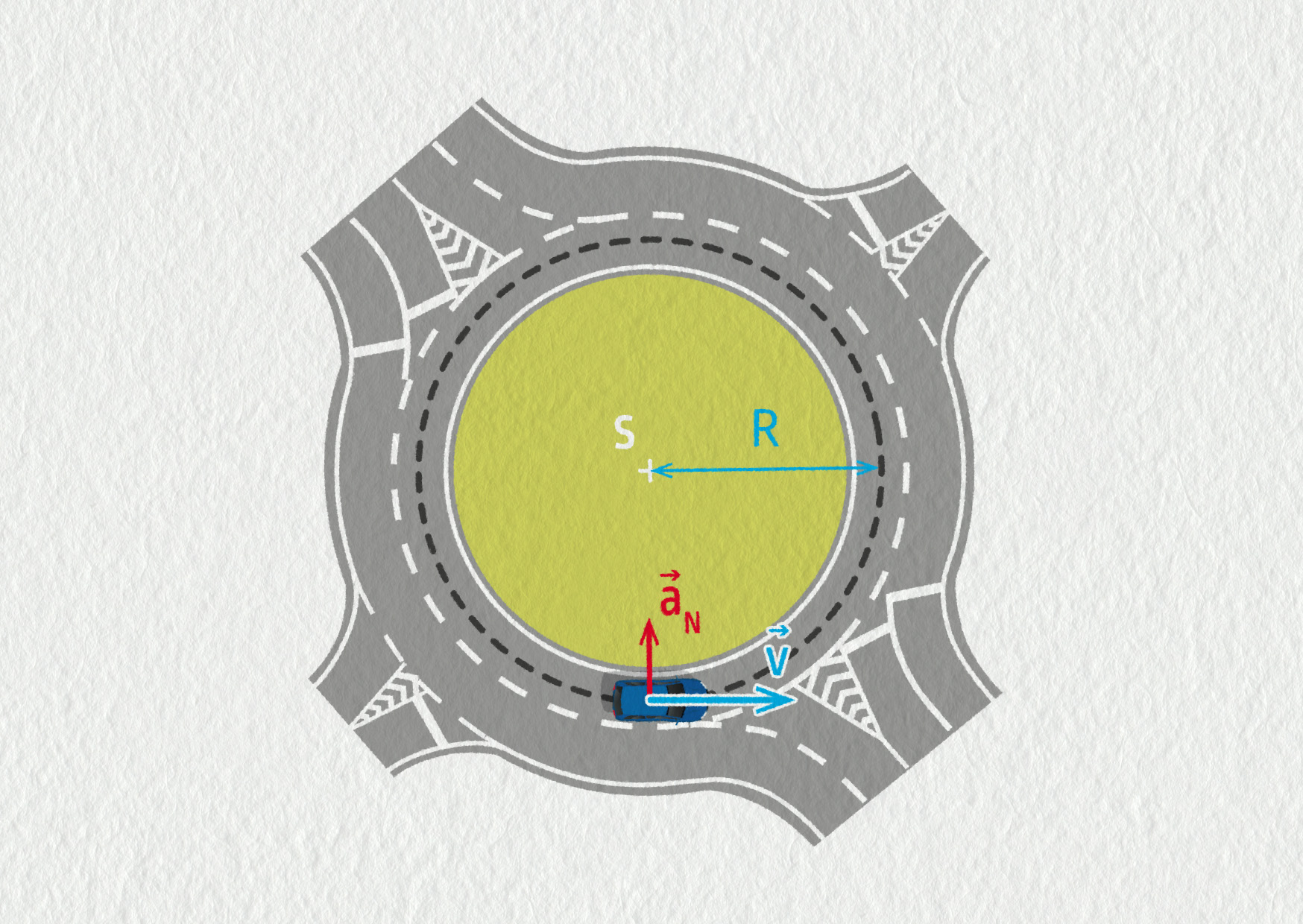
Auto jede po kruhovém objezdu rychlostí o stálé velikosti 26 km/h. Poloměr jeho trajektorie je 8,0 m.

1. Vypočítejte, za jak dlouho projede dokola celý objezd.
2. Vypočítejte velikost dostředivého zrychlení.
3. Situaci znázorněte obrázkem a vyznačte v něm vektor rychlosti a vektor zrychlení.
4. Mění se při tomto rovnoměrném pohybu veličina rychlost?

Člověk stojící na rovníku se otáčí spolu se Zemí. Jakou rychlostí se při tom pohybuje? Jaké je jeho zrychlení? Perioda otáčení Země je jeden den a poloměr Země na rovníku je 6 378 km.

„Když jsem v kosmické lodi obletěl Zemi, viděl jsem, jak je naše planeta krásná. Lidé, chraňme a rozmnožujme tuto krásu, ale neničme ji!“ pravil po přistání Jurij Alexejevič Gagarin, sovětský kosmonaut, první člověk ve vesmíru. Ke svému kosmickému letu odstartoval 12. dubna 1961 v lodi Vostok 1 z kosmodromu Bajkonur. Celý let trval dohromady 108 minut. Mezi vzletem a přistáním obletěl ve stavu bez tíže polovinu Země za 45,5 min po kruhové trajektorii ve výšce 327 km nad povrchem. Určete rychlost jeho pohybu. Při výpočtu použijte střední poloměr Země 6 371 km.

Pendolino projíždí obloukem o poloměru 1 200 m. Vypočítejte, jakou maximální rychlostí smí vlak tímto obloukem projíždět, jestliže zrychlení, které cestující pociťují, má velikost 0,9 m/s². Drážní předpisy nedovolují, aby cestujícího působilo větší nevykompenzované zrychlení než 0,65 m/s². Jakým způsobem je tato hodnota zrychlení kompenzována?

Automobil s průměrem pneumatik 32 cm jede po přímé silnici rychlostí 90 km/h.

1. Jaká je úhlová rychlost otáčení jeho pneumatik?
2. Jakou rychlostí vůči silnici se pohybuje vršek pneumatik?

3,5 palcová disketa rotuje v počítači s periodou 2,00 ⋅ 10⁻¹ s.

1. Určete úhlovou rychlost otáčení diskety,
2. rychlost bodu na okraji disku.
3. Má bod, který je blíže ke středu disku, menší, stejnou nebo vyšší rychlost než bod na okraji? Odpověď zdůvodněte.

Určete velikost normálového a tečného zrychlení tělesa, které se pohybuje po kružnici o poloměru 75 cm, rychlostí o velikosti 25 cm/s.

Hubbleův teleskop obíhá ve výšce 600 km nad zemským povrchem rychlostí 7,6 km/s. Určete jeho oběžnou dobu.

Krabí mlhovina je jeden z nejznámějších objektů na obloze. Jde o pozůstatky exploze supernovy pozorované již v roce 1054 Číňany. V roce 1968 jsme v její středu objevili pulsar – rychle rotující neutronovou hvězdu, která při každé otočce vysílá rádiové pulsy. Perioda tohoto pulsaru je 33 ms. Jaká je úhlová rychlost otáčení pulsaru v Krabí mlhovině? Kolik vykoná pulsar otáček za sekundu?

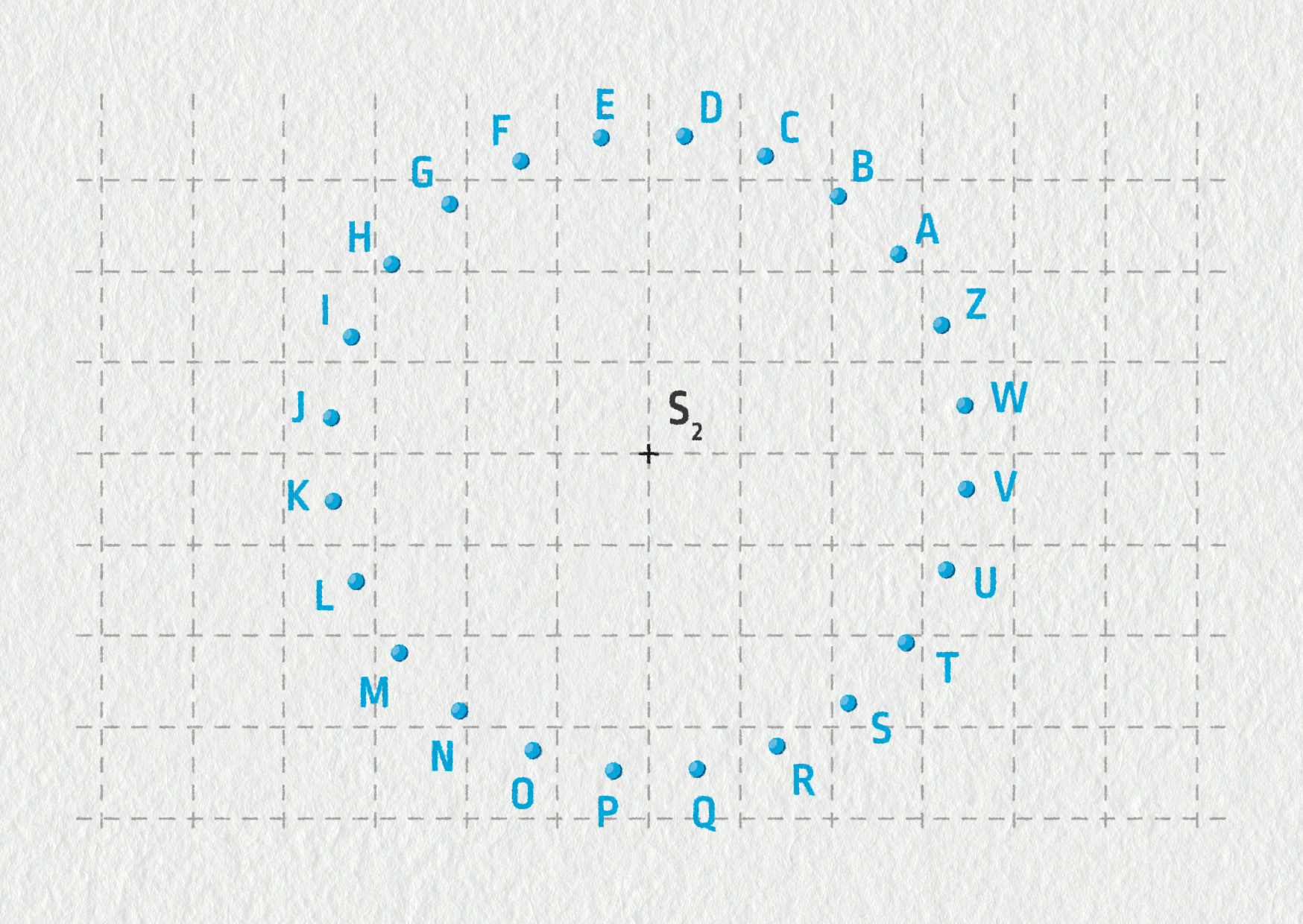
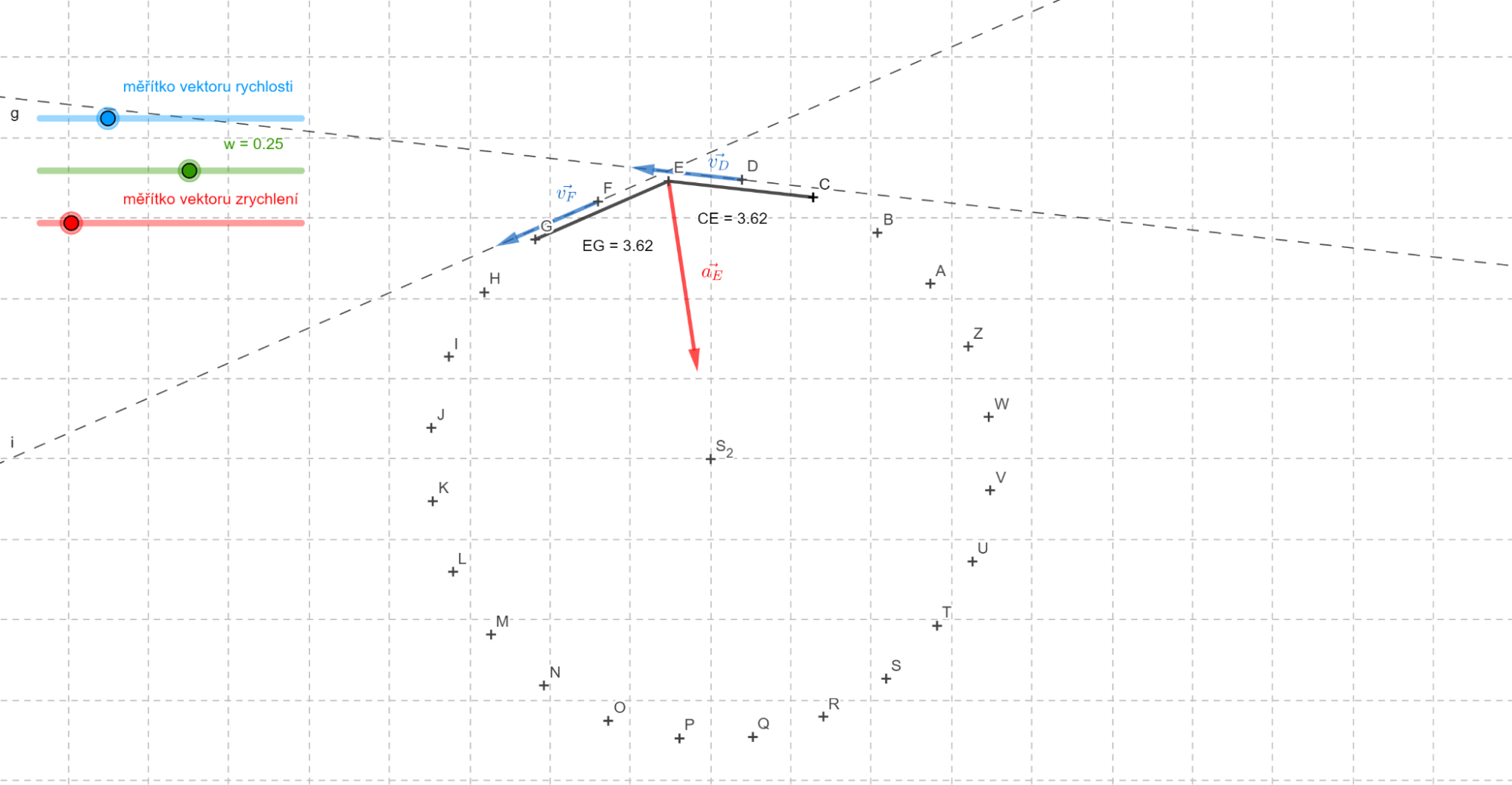
Na následujícím obrázku je záznam pohybu hmotného bodu umístěného na obvodu kola, které se otáčí kolem svého středu. Jednotlivé body byly zaznamenány s časovými rozdíly 25 ms. Jednotka vzdáleností na obrázku je 2 cm ve skutečnosti.

1. Vypočítejte velikosti rychlostí v bodech D a F a porovnejte je.
2. Narýsujte vektory rychlosti v bodech D a F. Zvolte vhodné měřítko.
3. Určete velikost zrychlení hmotného bodu v bodě E.
4. Narýsujte tento vektor do bodu E. Zvolte vhodné měřítko.
5. Jaký je směr vektoru zrychlení?
6. Jak se změní vektory rychlosti a zrychlení, jestliže časový interval mezi následujícími pozicemi je pouze 10 ms?

Zakreslete všechny síly, které na běžce při průběhu zatáčkou působí. Pro zjednodušení si běžce představme jako těleso, které se pohybuje po kruhové trajektorii konstantní rychlostí. Kam směřuje zrychlení běžce a která síla ho způsobuje?

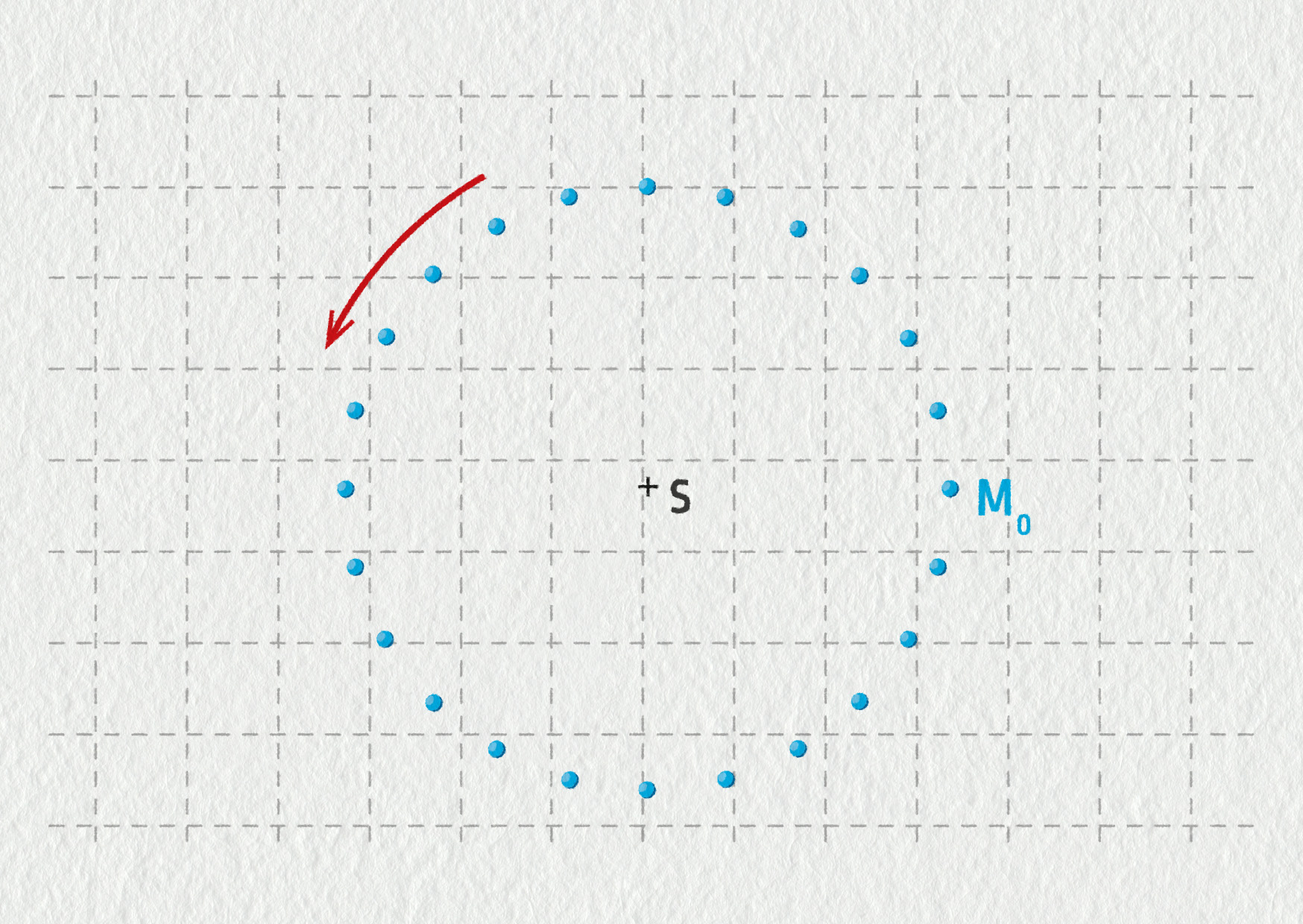
Astronauti jsou během výcviku podrobeni velkým zrychlením. K tomu se používá zařízení zvané centrifuga. Na obrázku vidíte jednu z centrifug ve Hvězdném městečku nedaleko Moskvy. Délka ramene je 18 m, maximální rychlost rotace je 38,6 otáček za minutu.

1. Vysvětlete princip centrifugy. Jakého maximálního zrychlení na ní lze dosáhnout?
2. Sestrojte do předchozího záznamu trajektorie centrifugy vektor zrychlení v libovolném bodě trajektorie. Dva po sobě jdoucí body jsou odděleny časem. Doporučené měřítko pro znázornění vektoru rychlosti: 1 cm pro 10 m/s, doporučené měřítko pro znázornění vektoru zrychlení: 1 cm pro 25 m/s².
3. V případě rovnoměrného pohybu po kružnici je vektor zrychlení dostředivý a pro jeho velikost platí \(a=v^2/R\). Odpovídá výsledek vašeho rýsování tomuto modelu?
4. Vytváří centrifuga velké zrychlení? Porovnejte výsledek rýsování s teoretickým maximálním zrychlením kabiny centrifugy.
5. Proč je vhodné umístit kabinu daleko od středu?

Na bobové dráze dosahují závodníci rychlosti až 150 km/h. Určete poloměr zatáčky, dosahuje-li přetížení při jejím průjezdu hodnoty \(4g\). Co tato hodnota znamená?

Tachometr jízdního kola snímá počet otáček předního kola za časovou jednotku. Jakou rychlost ukazuje displej tachometru, jestliže čidlo snímá 5,14 otáček za sekundu? Průměr kola i s pneumatikami je 70 cm.

Auto o hmotnosti 1 200 kg projíždí kruhovým objezdem o poloměru 25 m rychlostí 30,6 km/h. Která síla způsobuje, že auto zatáčí? Vypočítejte její velikost.

Určete, jak velkou gravitační silou přitahuje Země Měsíc. Hmotnost Měsíce je 7,35 ⋅ 10²² kg, jeho střední vzdálenost od Země 384 000 km a perioda oběhu po kružnici 27,3 dne.

Malá kovová kulička o hmotnosti 200 g je zavěšena na tenké niti o délce 80 cm. Vypočítejte tahovou sílu niti, pokud

1. kulička visí v klidu v nejnižší poloze,
2. kulička je rozhoupaná a prochází rychlostí 2 m/s rovnovážnou polohou.