Vodorovný pohyb
Ve všech příkladech dosazujte hodnotu \(g=10\ \mathrm{m/s^2}\).
Cvičení 1
Chlapec táhne sáňky o hmotnosti 6 kg vodorovnou silou o velikosti 15 N. Pohyb sáněk je rovnoměrný přímočarý a děje se ve vodorovné rovině. Určete velikosti všech sil působících na sáňky. Určete součinitel smykového tření mezi sáňkami a sněhem.
\(F_\mathrm{t}=15\ \mathrm{N}\); \(F_\mathrm{G}=60\ \mathrm{N}\); \(F_\mathrm{N}=60\ \mathrm{N}\); \(f=0{,}25\)
Cvičení 2
Fotbalový míč má hmotnost 450 g a leží na vodorovném hřišti. Určete všechny síly, které na něj působí.
\(F_\mathrm{G}=F_\mathrm{N}=4{,}5\ \mathrm{N}\)
Cvičení 3
Hokejový puk se po velmi kluzkém ledu pohybuje přímočaře téměř stálou rychlostí 30 m/s. Hmotnost puku je 170 g. Určete síly, které na puk působí.
\(F_\mathrm{G}=F_\mathrm{N}=1{,}7\ \mathrm{N}\)
Cvičení 4
Na siloměru je zavěšen měděný váleček. Siloměr ukazuje hodnotu 1,32 N. Jaká je hmotnost válečku? Jaký má váleček objem, je-li hustota mědi 8,96 g/cm3?
\(F_\mathrm{G}=F_\mathrm{T}=1{,}32\ \mathrm{N}\); \(m=132\ \mathrm{g}\); \(V=14{,}7\ \mathrm{cm^3}\)
Cvičení 5
Součinitel smykového tření \(f\) pro dřevo se dá snadno změřit. Vezmeme dřevěný špalík o hmotnosti 157 g a pomocí siloměru jej táhneme po vodorovné dřevěné podložce. Když je siloměr držen vodorovně a špalík vykonává pohyb rovnoměrný a přímočarý, ukazuje siloměr hodnotu 0,52 N. Jaký je součinitel smykového tření dřeva na dřevě?
\(F_\mathrm{T}=F_\mathrm{t}\); \(f=0{,}33\)
Cvičení 6
Jak velkou vodorovnou silou musíme tlačit na těžkou bednu o hmotnosti 50 kg, chceme-li ji posouvat rovnoměrným přímočarým pohybem po vodorovné podlaze? Součinitel smykového tření je 0,65.
325 N
Cvičení 7
Běžné SUV má hmotnost 1 500 kg a z klidu na rychlost 100 km/h se rozjede za 10 s. Vypočítejte tahovou sílu motoru.
Cvičení 8
Auto s největším zrychlením na světě je Porsche 918 Spyder. Při hmotnosti 1,7 t zrychlí z 0 na 100 km/h za pouhých 2,2 s. Vypočítejte průměrnou tahovou sílu motoru. Údaj se vztahuje k přímočarému pohybu po vodorovné silnici, zanedbáváme odpor vzduchu.
Cvičení 9
Při odkopu od branky působí noha brankáře na míč průměrnou silou \(F=297\ \mathrm{N}\). S jakým zrychlením se míč pohybuje, je-li jeho hmotnost 450 g? Jakou rychlost míč získá, působí-li noha po dobu 0,05 s? Zanedbejte vliv ostatních sil.
- 660 m/s2
- 33 m/s
Cvičení 10
Tatrovka jede po vodorovné silnici rychlostí \(v_0=65\ \mathrm{km/h}\). V určitém okamžiku vstoupí do vozovky nepozorný chodec a řidič začne prudce brzdit. Maximální síla, kterou brzdy vyvinou, je 66 kN. Vypočítejte zrychlení a brzdnou dráhu (tj. dráhu potřebnou k zastavení). Hmotnost plně naložené Tatrovky je 22 t.
- −3 m/s2
- 54 m
Cvičení 11
K čemu slouží ABS čili Anti-lock Brake System? Při prudkém brzdění se kola u starých aut, která nemají ABS, zastaví a kloužou po asfaltu smykem se součinitelem dynamického tření \(f_\mathrm{d}=0{,}55\). Pokud je antiblokovací systém ABS aktivní, kola neprokluzují a je možné využít maximální hodnoty součinitele statického tření \(f_\mathrm{s}=0{,}60\). Spočítejte pro oba případy zrychlení a brzdnou dráhu při vodorovném pohybu s počáteční rychlostí \(v_0=90\ \mathrm{km/h}\).
- 5,5 m/s2 a 56,8 m
- 6,0 m/s2 a 52,1 m
Obě dvě zrychlení mají zápornou hodnotu.
Cvičení 12
K čemu jsou dobré autosedačky pro děti? Místo aby maminka usadila dítě o hmotnosti 9 kg do dětské sedačky, drží je na klíně. Při nehodě narazí auto v rychlosti 45 km/h do překážky a zastaví se za 0,1 s. Jakou silou by musela maminka dítě držet, aby se pohyb dítěte zastavil spolu s autem a s ní? Co se stane ve skutečnosti?
Cvičení 13
Pouliční lampa o hmotnosti 42 kg je zavěšena nad středem ulice (viz obrázek). Napnutá lana svírají s vodorovným směrem úhel 15°. Určete velikosti sil, které napínají lana.
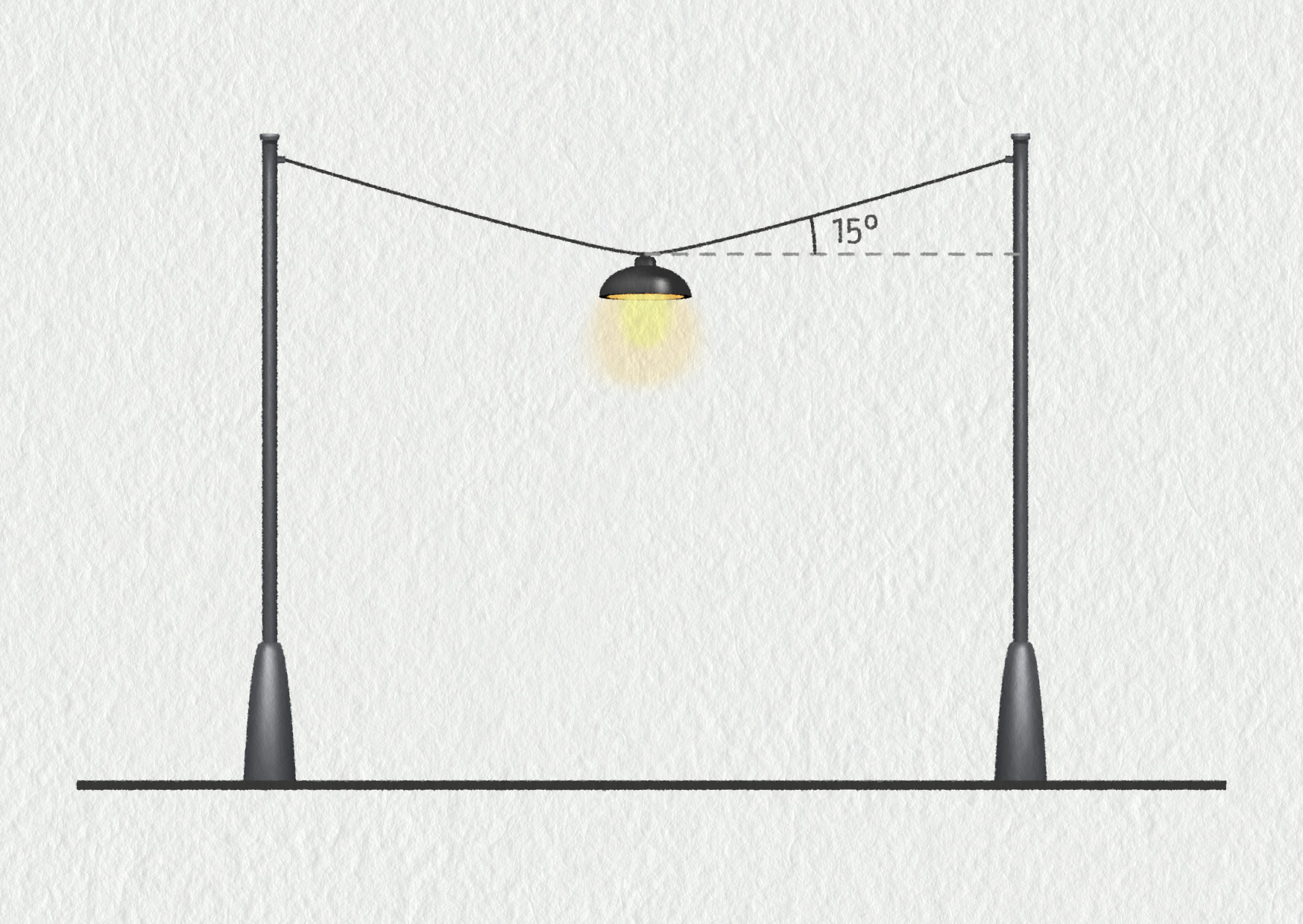
Zdroj
Cvičení 14
V kartézské soustavě souřadnic máme síly \(\Vec{F}_1=(2;6)\ \mathrm{N}\) a \(\Vec{F}_2=(-1{,}5;3)\ \mathrm{N}\).
- Zakreslete vektory \(\Vec{F}_1\) a \(\Vec{F}_2\) a určete úhel, který spolu svírají.
- Sestrojte a poté určete souřadnice vektoru \(\Vec{F}_3=\Vec{F}_1-2\Vec{F}_2\).
- Jaký je vztah mezi složkami \(F_{3x}\), \(F_{1x}\), \(F_{2x}\)? A mezi \(F_{3y}\), \(F_{1y}\), \(F_{2y}\)?
-
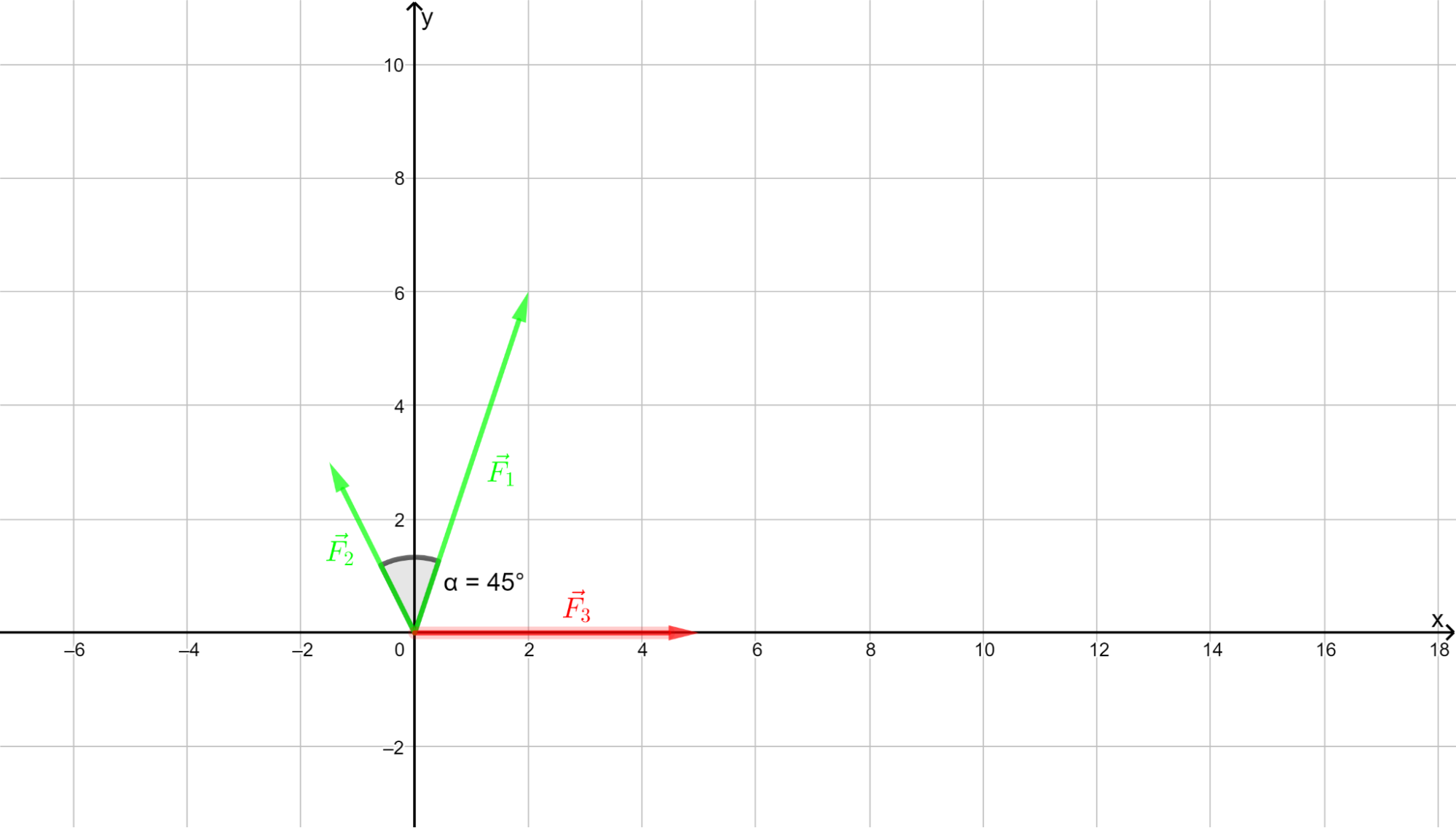
15.35 – Znázornění sil
Zdroj - \(F_{3x}=F_{1x}-2F_{2x}\) a \(F_{3y}=F_{1y}-2F_{2y}\)
Cvičení 15
Na těleso působí tři síly různých směrů. Působí v jeho těžišti T, které můžeme ztotožnit s počátkem soustavy souřadnic. Je dáno \(\Vec{F}_1=(-8;3)\ \mathrm{N}\), \(\Vec{F}_2\) svírá s osou \(x\) úhel 45° a má velikost \(8\sqrt2\ \mathrm{N}\). Určete graficky a potvrďte výpočtem složky vektoru třetí síly \(\Vec{F}_3\) takové, aby se všechny tři síly navzájem vyrušily.
\(\Vec{F}_3=(0,-11)\ \mathrm{N}\)
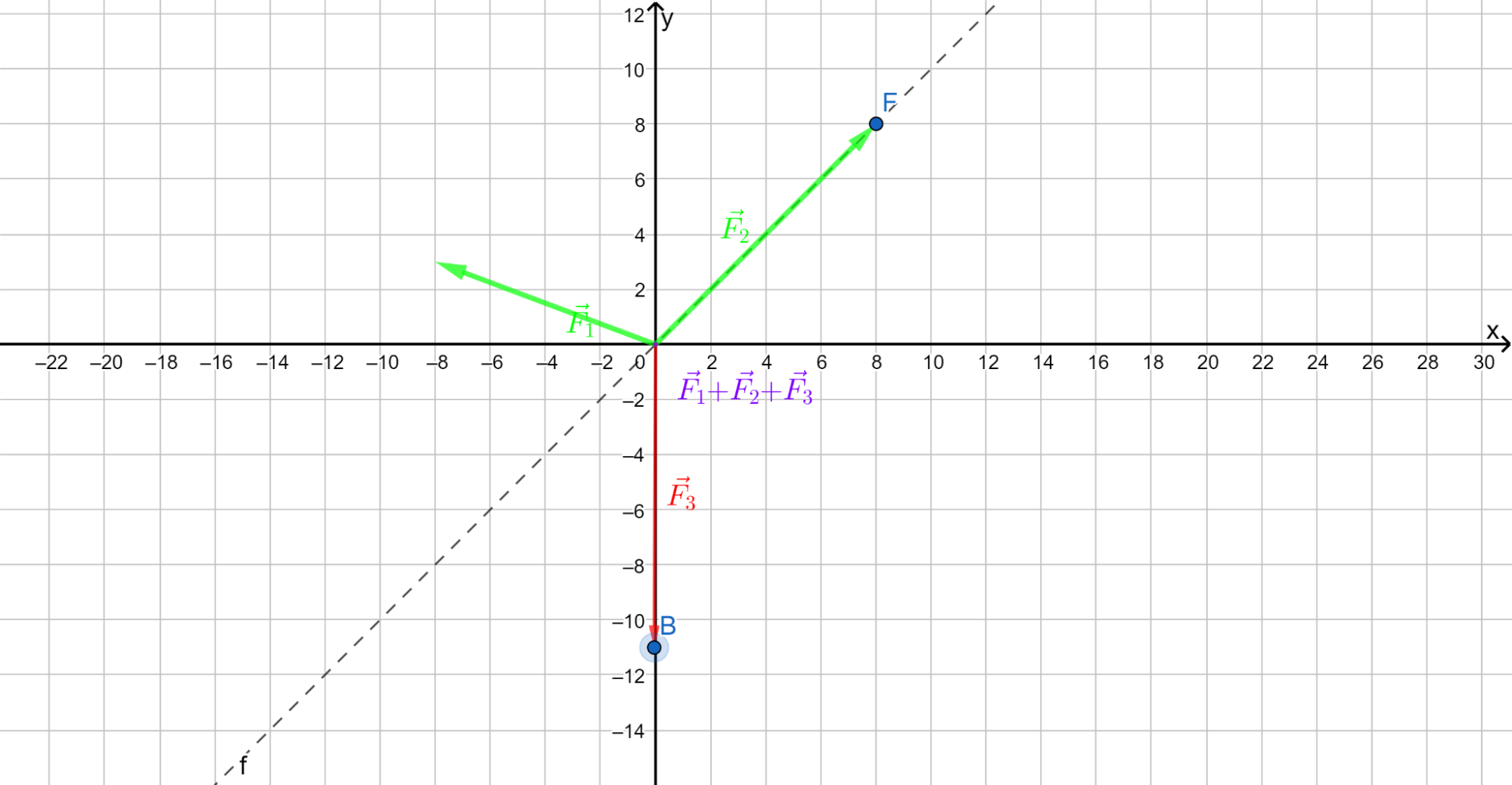
Zdroj

