Zrychlení
Cvičení 1
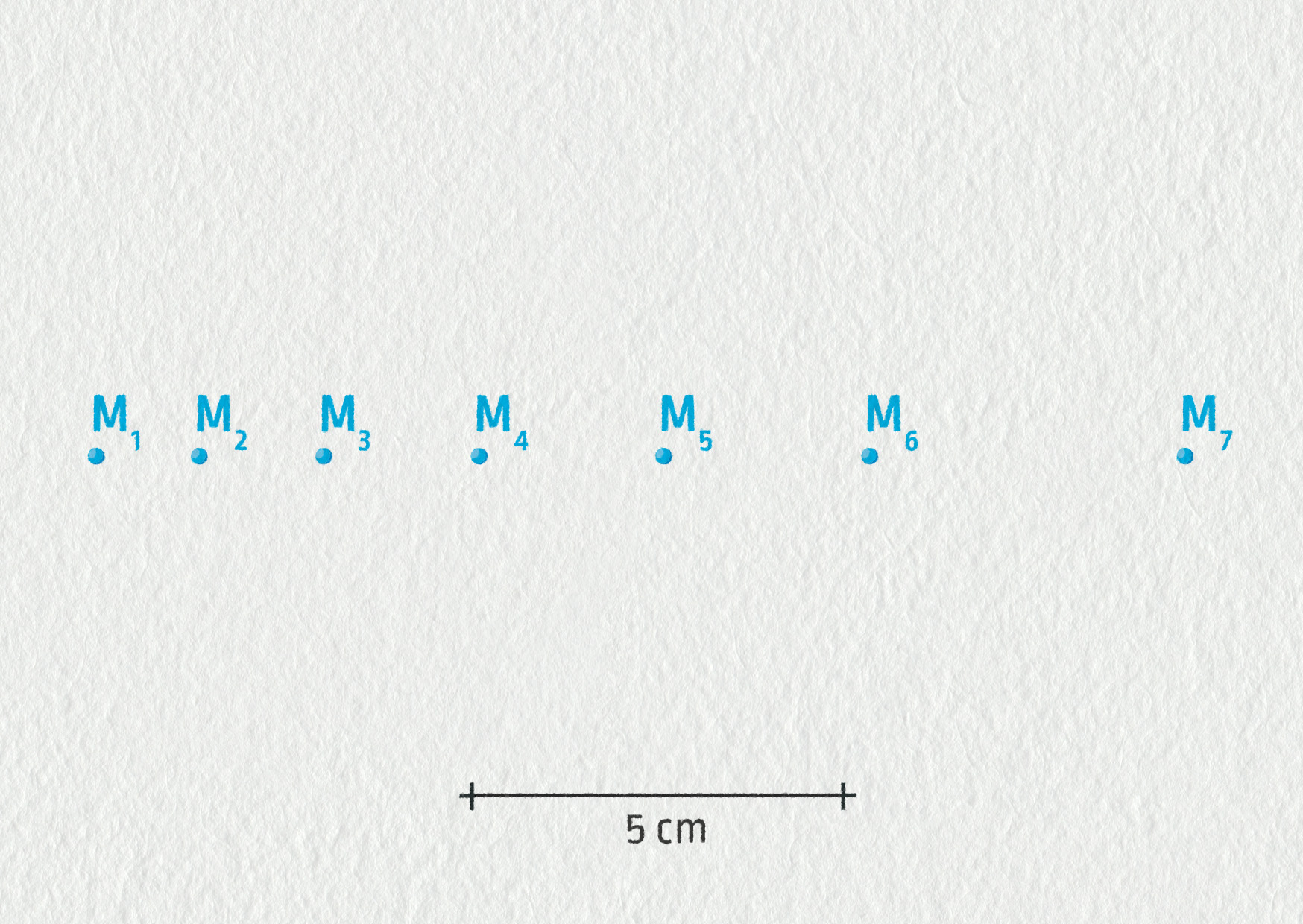
Prohlédněte si zákres několika po sobě jdoucích poloh tělesa (PDF ke stažení zde).
Zdroj
- Jaký pohyb vykonává těleso? Zdůvodněte.
- Určete zrychlení tělesa v bodě M3 a v bodě M6. Mezi označením dvou po sobě jdoucích poloh uplynulo 20 ms.
- Těleso vykonává přímočarý, zrychlený pohyb. Po sobě jdoucí pozice jsou od sebe stále více vzdáleny.
- a3 = 9,4 m/s2, a5 = 15,6 m/s2
Cvičení 2
Mirek studoval pohyb kapky vody v oleji. Nejprve naplnil odměrný válec rostlinným olejem a poté na jeho hladinu umístil malou kapku vody. Když do ní lehce strčil prstem, začala se kapička pohybovat směrem dolů. V okamžiku, kdy procházela kolem značky 100 ml na odměrném válci, začal Mirek měřit čas a ten zaznamenal vždy, když kapička míjela další značku (90 ml, 80 ml, …). Naměřené hodnoty jsou uvedeny v tabulce.
| t (s) | 0 | 1,9 | 3,7 | 5,8 | 8,1 | 10,0 | 11,9 | 14,2 | 16,4 | 18,2 | 20,1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| x (cm) | 0 | 1,7 | 3,3 | 5,0 | 6,7 | 8,4 | 10,0 | 11,7 | 13,4 | 15 | 16,7 |
- Vysvětlete, proč kapka držela na hladině vody a proč se po postrčení začala pohybovat dolů.
- Dokážete určit, jak Mirek získal souřadnici popisující pohyb kapky vody?
- Vypočítejte rychlost kapky v časech \(t_4=5{,}8\ \mathrm{s}\) a \(t_7=10{,}2\ \mathrm{s}\).
- Co můžete říci o druhu tohoto pohybu a proč? Odpovídá tento výsledek reálné situaci?
- Kapka byla držena na hladině oleje jeho povrchovým napětím. Když se dostala pod hladinu, začala klesat, protože její hustota je větší než hustota oleje.
- Mirek změřil vzdálenost mezi několika dílky na odměrném válci a podělil počtem vzdáleností.
- \(v_4=0{,}77\ \mathrm{cm/s}\) \(v_7=0{,}79\ \mathrm{cm/s}\);
- pohyb je přímočarý a patrně rovnoměrný, protože rychlosti \(v_4\) a \(v_7\) jsou prakticky stejné velikosti. Výsledek odpovídá reálné situaci, protože odporová síla při pohybu v kapalině je srovnatelná s tíhou kapičky.
Cvičení 3
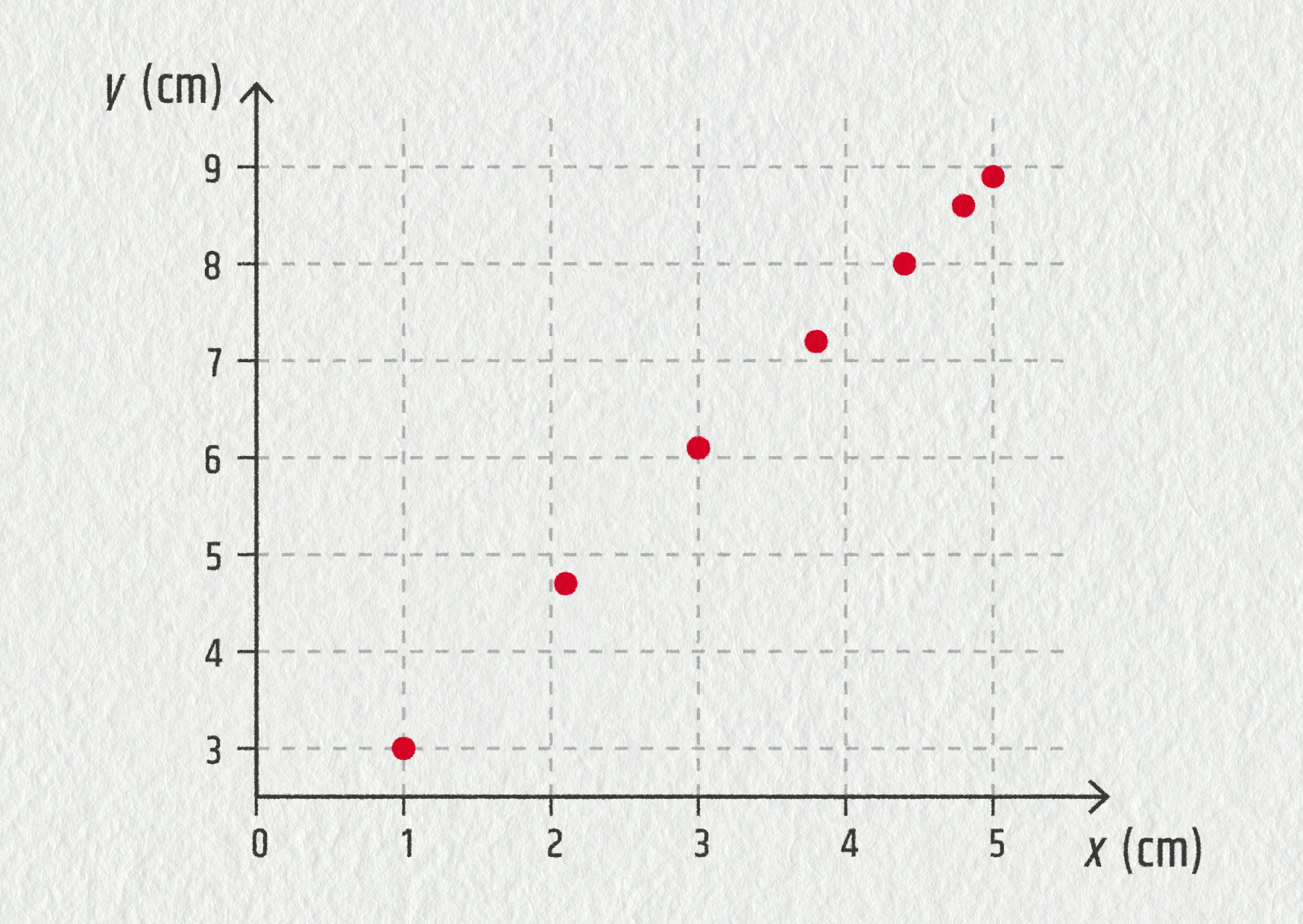
Těleso vykonávalo pohyb, jehož souřadnice jsou zaznamenány v následující tabulce.
| t (s) | x (cm) | y (cm) |
|---|---|---|
| 0 | 1,0 | 3,0 |
| 0,3 | 2,1 | 4,7 |
| 0,6 | 3,0 | 6,1 |
| 0,9 | 3,8 | 7,2 |
| 1,2 | 4,4 | 8,0 |
| 1,5 | 4,8 | 8,6 |
| 1,8 | 5,0 | 8,9 |
- Zakreslete jednotlivé polohy tělesa na papír. (Sestrojte graf trajektorie pohybu tělesa.) Jaký pohyb těleso vykonává?
- Jak budete postupovat, když chcete určit rychlost tělesa v časovém okamžiku \(t=0{,}6\ \mathrm{s}\)? Určete velikost této rychlosti.
- Podobně určete rychlost tělesa v okamžiku \(t=1{,}2\ \mathrm{s}\).
- Jaké je zrychlení tělesa v čase \(t=0{,}9\ \mathrm{s}\)?
- řešení je zakresleno na obrázku, těleso koná přímočarý zpomalený pohyb;
- máme v principu dvě možnosti: buďto určíme velikost rychlosti pomocí měření vzdálenosti dvou bodů sousedících se studovaným bodem na našem grafu, nebo v tabulce určíme složky rychlosti a z nich potom velikost rychlosti, \(v(t=0{,}6\ \mathrm{s})=5{,}0\ \mathrm{cm/s}\);
- \(v(t=1{,}2\ \mathrm{s})=2{,}9\ \mathrm{cm/s}\);
- \(a(t=0{,}9\ \mathrm{s})=3{,}6\ \mathrm{cm/s}^2\)
Zdroj
Cvičení 4
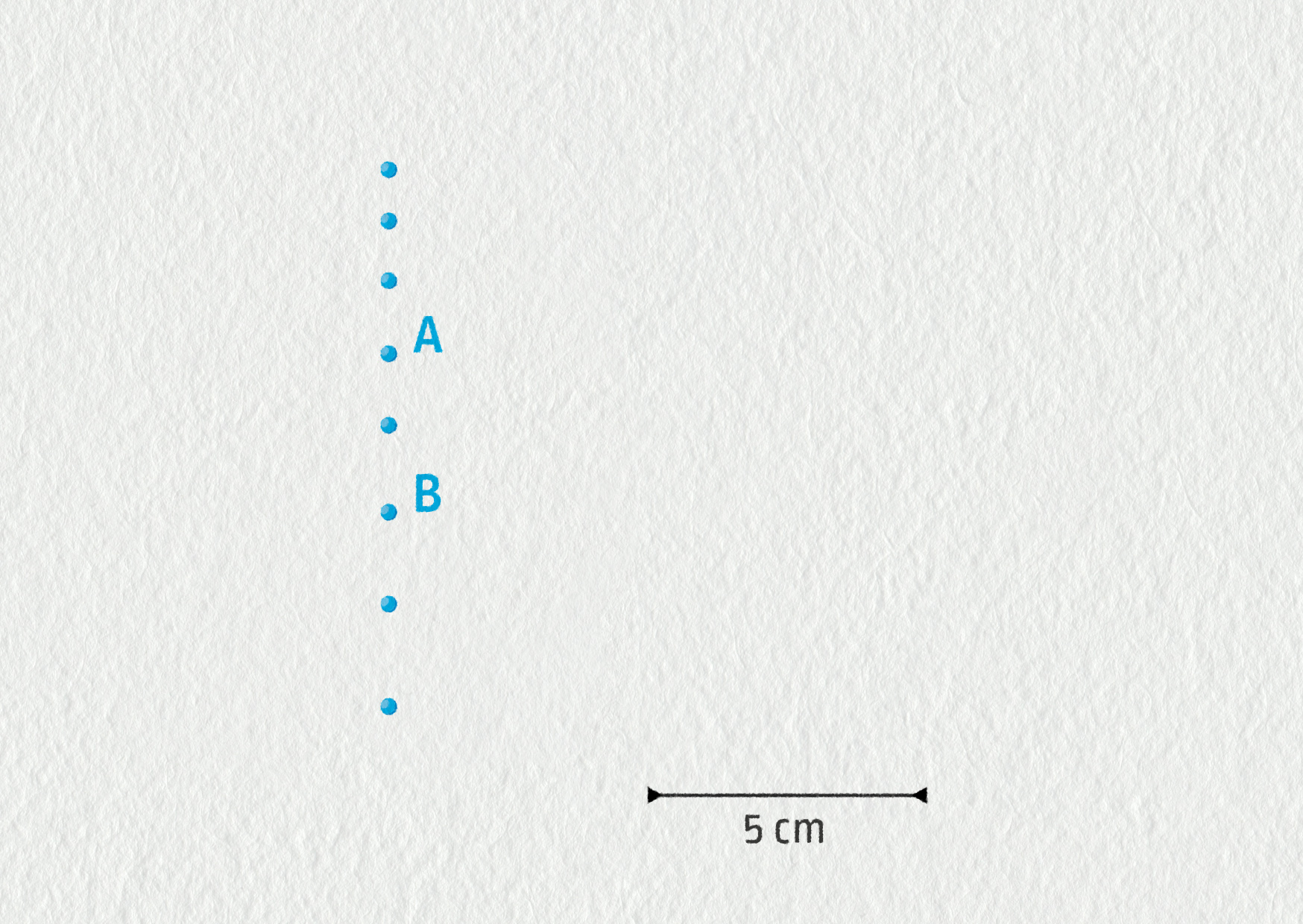
Vojta studoval ve fyzikální laboratoři pohyb tělesa. Záznam videokamerou převedl do počítače a získal přiložený záznam (ke stažení zde). Tento záznam je v měřítku 1 : 10. Doba, která odděluje dvě sousední značky, je \(\tau=40\ \mathrm{ms}\) (25 FPS). Těleso se pohybuje směrem od A k B.
Zdroj
- Vyberte si soustavu souřadnic včetně počátku a zakreslete ji do obrázku.
- Znázorněte polohové vektory tělesa v bodech A a B.
- Jaký je směr vektoru rychlosti v bodech A a B?
- Spočítejte rychlost tělesa v těchto bodech.
- Zakreslete do obrázku tyto dva vektory rychlosti. Nezapomeňte uvést měřítko.
- Jde o pohyb rovnoměrný nebo zrychlený? Odpověď zdůvodněte, vypočítejte velikost zrychlení tělesa.
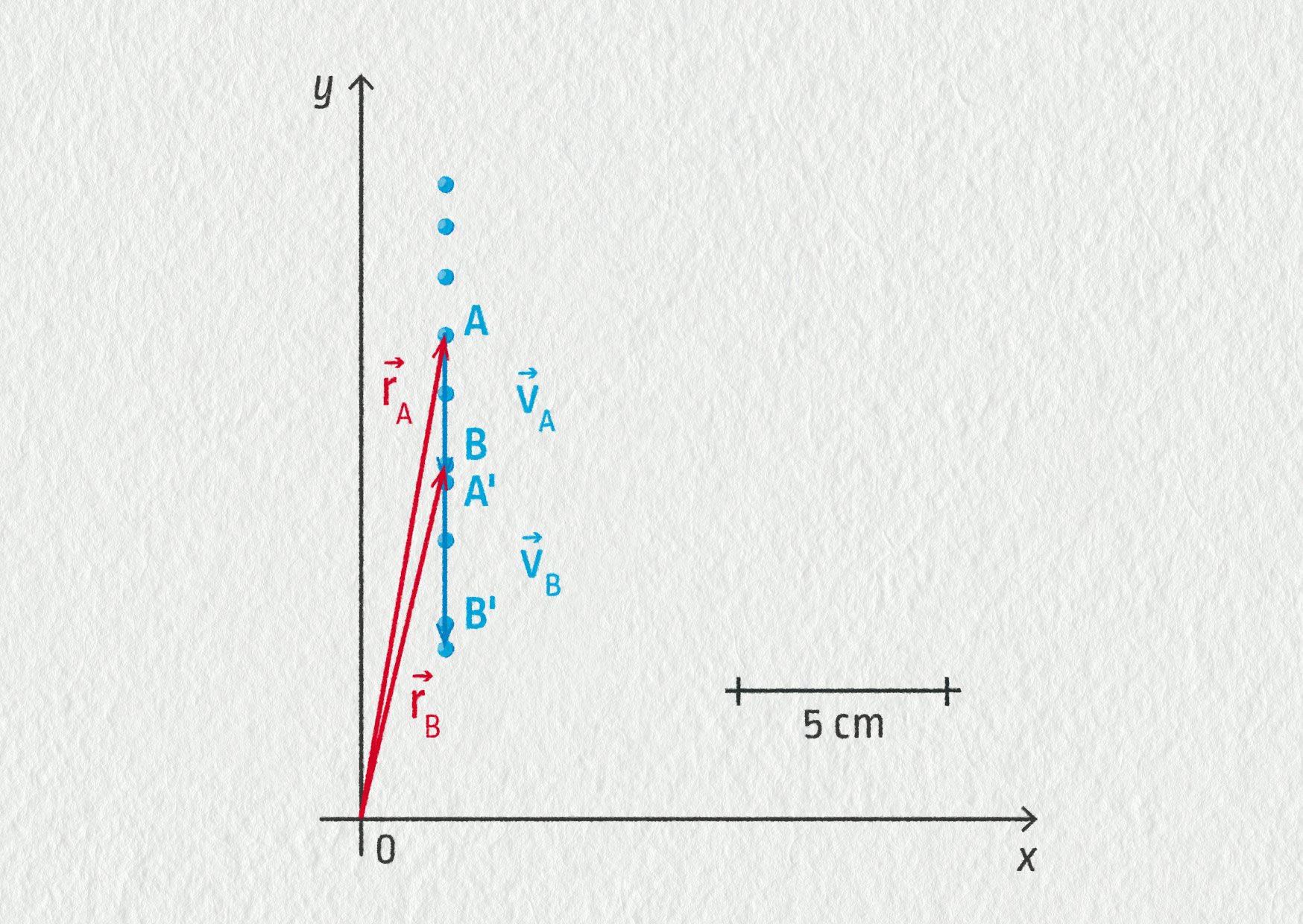
- viz obrázek 14.63;
- viz obrázek 14.63;
- vektory rychlosti ve studovaných bodech jsou orientovány směrem dolů, tedy od A k B;
- \(v_A=3{,}5\ \mathrm{m/s}\), \(v_B=4{,}4\ \mathrm{m/s}\);
- viz obrázek 14.63;
- měřítko: \(1\ \mathrm{cm}\ \widehat{=}\ 1{,}0\ \mathrm{m/s}\);
- pohyb je zrychlený, velikost rychlosti narůstá, \(a=11{,}3\ \mathrm{m/s}^2\)
Zdroj

