Průměrná a okamžitá rychlost
Úkol:
- Změřte průměrnou rychlost autíčka klasickou metodou.
- Měřte průměrnou rychlost kuličky na vodorovné rovině pomocí optických závor.
Vybavení: metr, stopky, optická závora (2 ks), ocelová kulička, autíčko na baterie
Aktivita č. 1 – průměrná rychlost klasickou metodou
V této aktivitě použijeme k určení průměrné rychlosti klasickou metodu, tedy využijeme metr a stopky. Vzhledem k ručnímu měření času je vhodné studovat pohyb autíčka, které jezdí pomalu. Vyznačíme na stole vzdálenost \(d=1\ \mathrm{m}\) a měříme dobu, za kterou autíčko urazí vyznačenou vzdálenost. Výsledky zapíšeme do tabulky, měření několikrát opakujeme a vypočítáme průměrnou hodnotu průměrné rychlosti autíčka včetně nejistot měření.
Aktivita č. 2 – průměrná a okamžitá rychlost (optická závora)
Pro určení průměrné rychlosti tělesa, jehož pohyb je tak rychlý, že ruční měření nedává dostačující výsledky, použijeme dvě optické závory umístěné na vzdálenost \(d\). Pomocí nich určíme čas \(t_1\), kdy těleso „vjede“ do měřeného úseku, a čas \(t_2\), kdy z něj „vystoupí“. Velikost průměrné rychlosti opět spočítáme z definice \(v_\mathrm{p}=d/(t_2-t_1)\).

Zdroj
Postup: Připravte si nakloněnou rovinu a umístěte na ni dvě optické závory připojené k počítači (viz schéma experimentu).
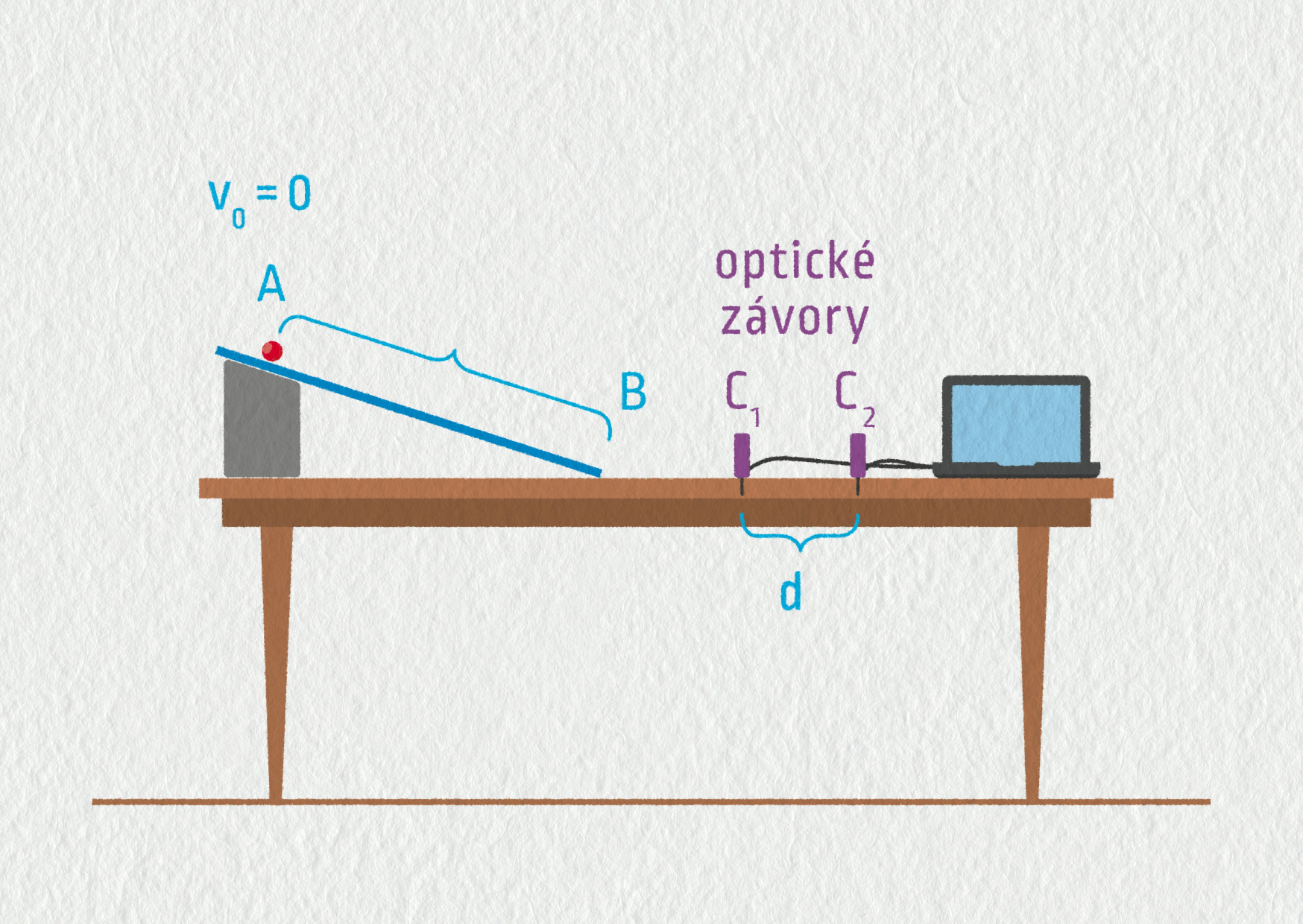
Zdroj
Uvolněte kuličku bez počáteční rychlosti z místa A na nakloněné rovině (vzdálenost \(l\) je konstantní) a pomocí optických závor určete průměrnou rychlost kuličky na vzdálenosti \(d\). Při opakování experimentu změňte vzdálenost \(d\) mezi závorami a opět vypočítejte průměrnou rychlost.
Otázky:
- Jak se mění velikost průměrné rychlosti v závislosti na vzdálenosti \(d\) mezi závorami?
- Co z toho můžeme usoudit o pohybu kuličky?
- Jakou máme tedy volit vzdálenost \(d\) při měření průměrné rychlosti?
- Když bude tato vzdálenost velmi malá, co můžeme říci o časech \(t_1\) a \(t_2\)?
- Můžeme změřit průměrnou rychlost kuličky za použití jedné optické závory?

