V předchozím textu jsme se naučili matematicky popsat harmonickou rovinnou vlnu a nyní se seznámíme s tím, co vlny obecně „umí“. Projdeme fyzikální jevy, které jsou pro vlny typické – podle nich poznáme, že daný objekt má vlnovou povahu. Patří mezi ně:
- odraz vlnění,
- lom vlnění,
- Dopplerův jev,
- ohyb vlnění a
- interference.
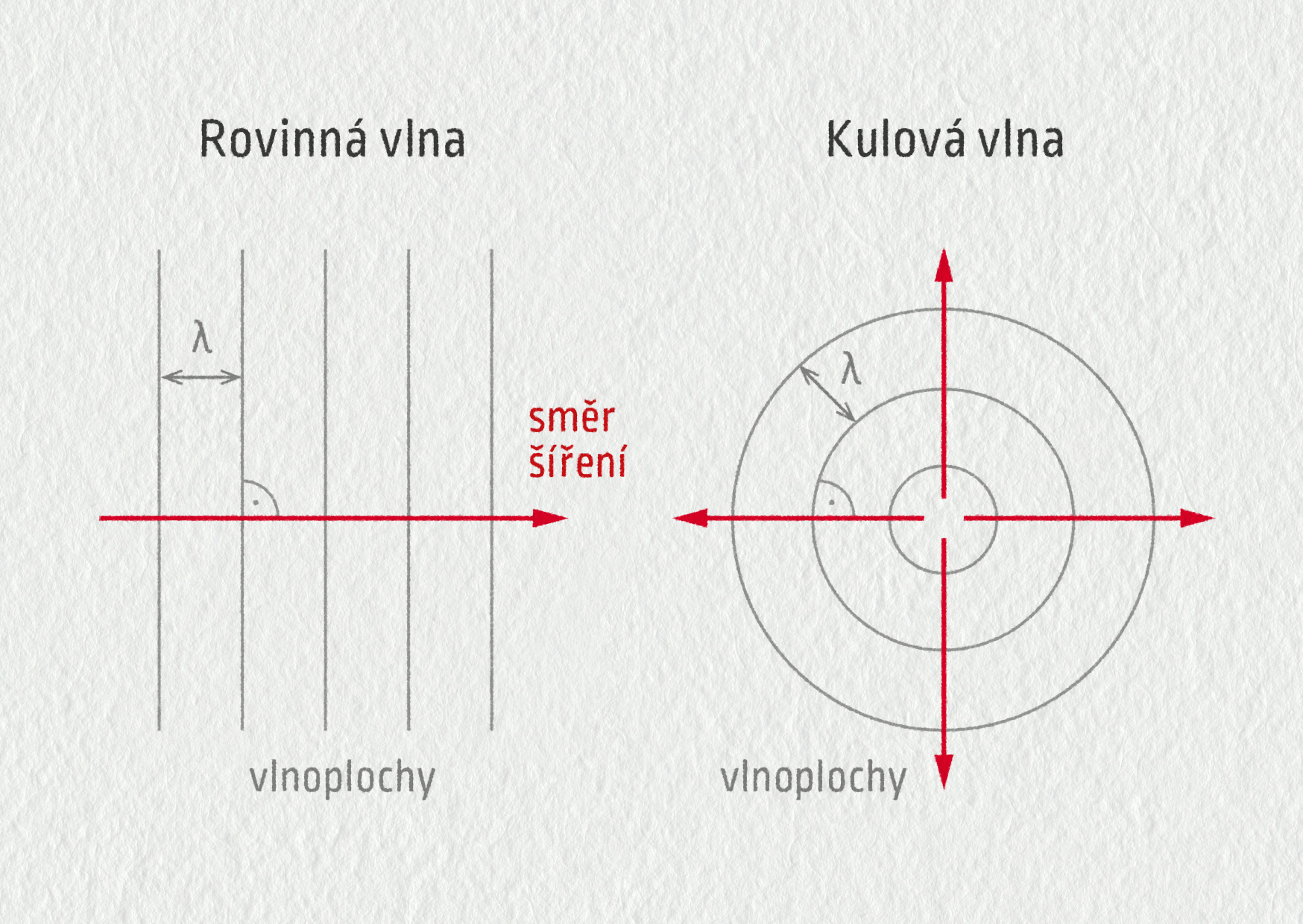
Abychom získali i vizuální představu, k čemu vlastně dochází, budeme ve schématech znázorňovat vlny pomocí tzv. vlnoploch. Vlnoplochy jsou křivky nebo plochy spojující místa, kde částice prostředí mají v daný okamžik vzájemně stejnou fázi. Vlnoplochy tvoří například hřbety vln na vodní hladině.
Zdroj
Odraz vlnění
Odraz vlnění nastává na rozhraní dvou prostředí, kde se skokově mění jejich fyzikální vlastnosti. Typickým příkladem je odraz zvuku od stěny v místnosti, odraz seismických vln na rozhraní mezi pevnou zemskou kůrou a kapalným pláštěm nebo odraz ultrazvuku na rozhraní dvou tělesných orgánů. Během odrazu se mění směr šíření, naopak frekvence a vlnová délka zůstávají zachovány.
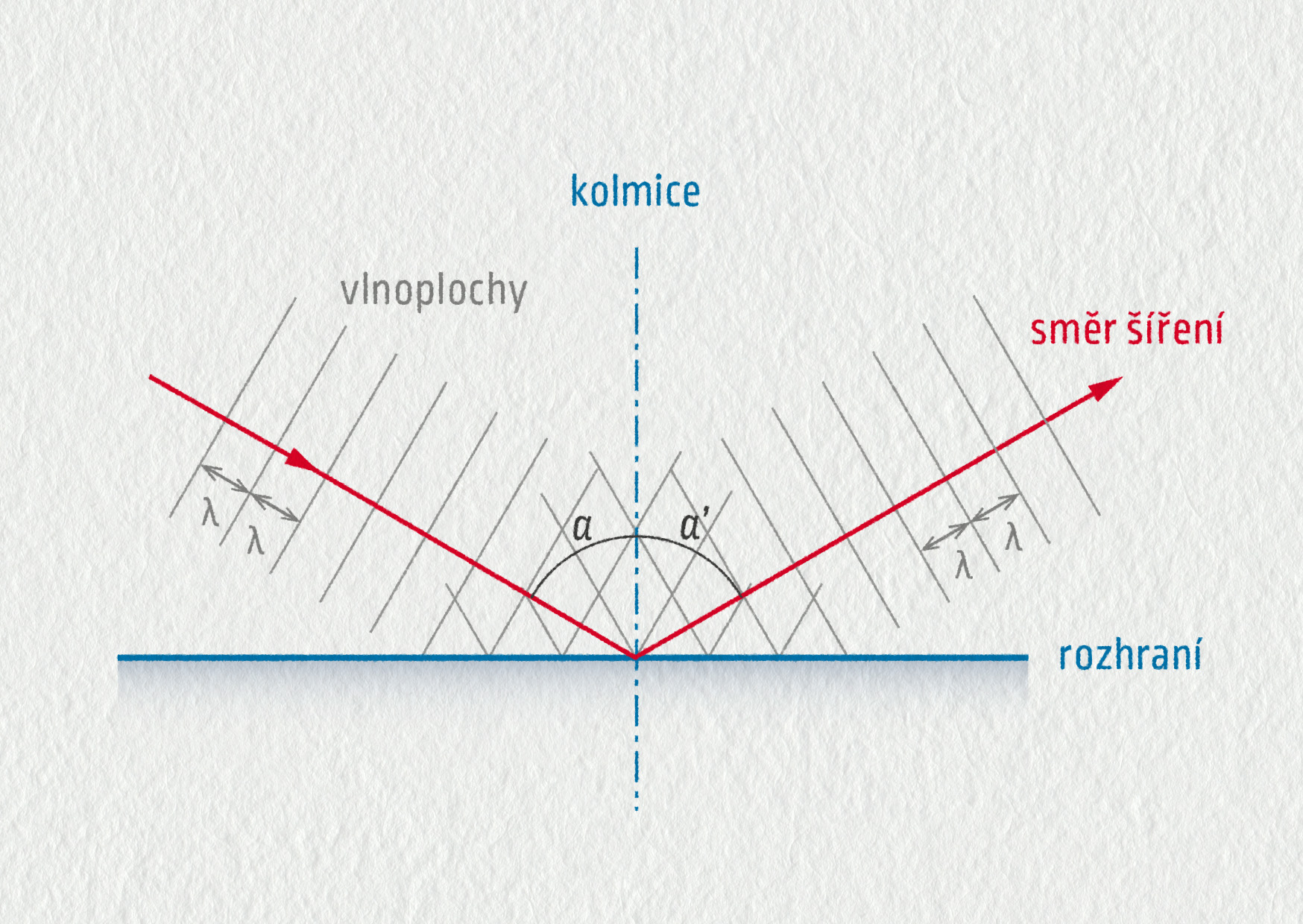
Situace je schematicky znázorněna na obrázku 22.29. Vlna přichází k rozhraní pod úhlem dopadu \(\alpha\) a odráží se pod úhlem odrazu \(\alpha' \). Ve fyzice je zvykem tyto úhly měřit od kolmice k rozhraní. Platí zákon odrazu \(\alpha'=\alpha\). Všimněte si, že vlnoplochy zůstávají na rozhraní spojité (například hřeben odražené vlny navazuje na hřeben vlny dopadající).
Zdroj
Sonar umístěny na rybářské lodi vyslal krátký ultrazvukový signál směrem ke dnu a zaregistroval dvě odražené vlny 0,21 s a 0,27 s od vyslání. Určete hloubku moře a hloubku, v níž se nachází hejno ryb. Rychlost šíření ultrazvuku ve vodě je 1,48 ⋅ 103 m/s.

Zdroj
Rybářský sonar funguje na principu ozvěny. Krátký ultrazvukový signál je vyslán k překážce, na níž se odráží. Sonar měří dobu \(t\) mezi vysláním a přijetím odražené vlny. Vlnění přitom urazí dráhu \(s=vt\), která je dvojnásobkem vzdálenosti mezi zdrojem a překážkou – viz obrázek 22.31.
Číselně vyjádřeno
\[\begin{aligned} s_1&=vt_1=1{,}48\cdot10^{3}\ \mathrm{m/s}\cdot0{,}21\ \mathrm{s}=310\ \mathrm{m}\;,\\ s_2&=vt_2=1{,}48\cdot10^{3}\ \mathrm{m/s}\cdot0{,}27\ \mathrm{s}=400\ \mathrm{m}\;. \end{aligned}\]Hejno ryb se nachází v hloubce 155 m, hloubka moře je 200 m.

Zdroj
Odraz vlnění v praxi

Zdroj

Zdroj
Zdroj
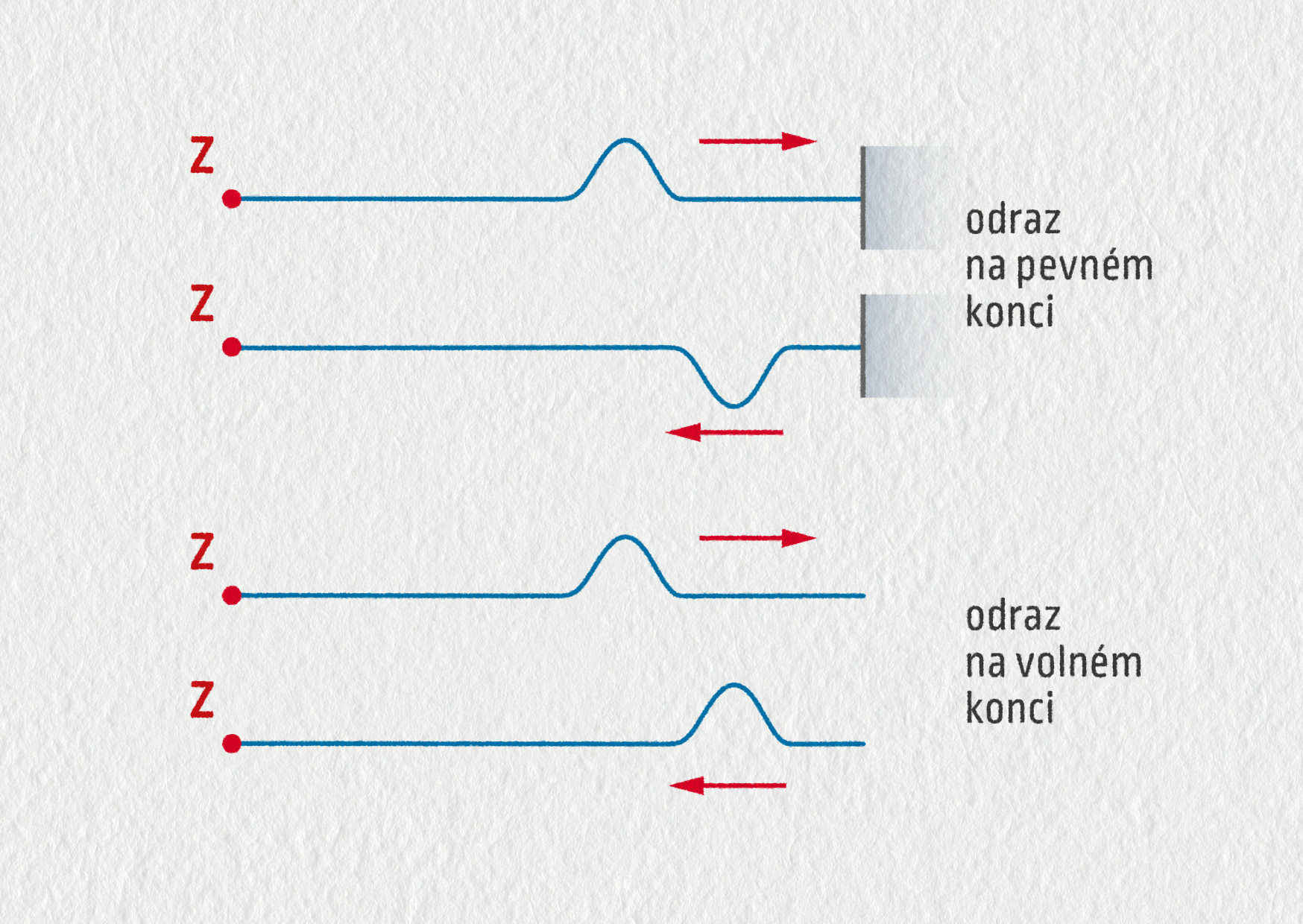
Kromě zákona odrazu a spojitosti vlnoploch na rozhraní souvisí s odrazem ještě jedna fyzikální zajímavost. Pokud se vlna šíří k okraji prostředí a ten není upevněn (konec je volný a může kmitnout), odražená vlna se vrací zpět se stejnou fází. Můžete to pozorovat, například když prudce trhnete volně ležící zahradní hadicí. Pokud je ovšem okraj upevněn tak, že kmitnout nemůže (pevný konec), vrací se odražená vlna s opačnou fází. To nastává například u struny na kytaře. Jak uvidíme dále, dopadající a odražená vlna se skládají, což vede k dalším zajímavým jevům.
Zdroj
Lom vlnění
Lom spočívá ve změně směru šíření vlnění na rozhraní dvou prostředí. Je přímým důsledkem změny rychlosti šíření při přechodu z jednoho prostředí do druhého.
Zdroj
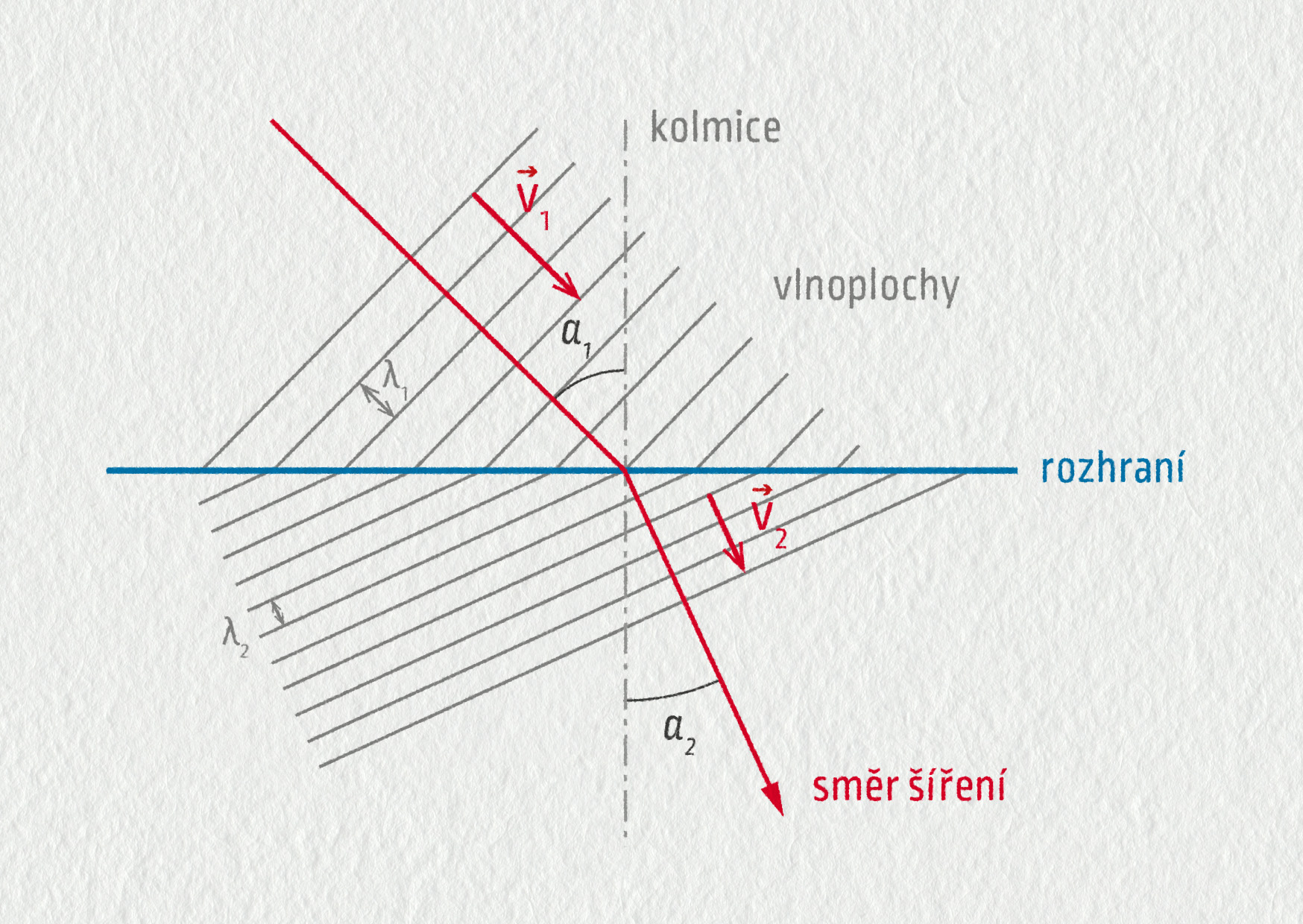
Situace je znázorněna na obrázku 22.34. Rovinná vlna přichází k rozhraní pod úhlem dopadu \(\alpha_1\) (měřeným od kolmice). Frekvence vln \(f\) před i za rozhraním zůstává stejná, takže pokud se mění rychlost šíření \(v\), musí se podle vztahu \(v=\lambda f\) změnit i vlnová délka \(\lambda\). Na rozhraní zůstává vlna spojitá (například hřeben dopadající vlny „pokračuje“ jako hřeben vlny lomené), takže změna vlnové délky nutně vede ke změně směru šíření. Jsou-li \(v_1\) a \(v_2\) rychlosti šíření v prvním a druhém prostředí, splňuje úhel lomu \(\alpha_2\) (měřený od kolmice) podmínku
\[ \frac{\sin\alpha_1}{\sin\alpha_2} = \frac{v_1}{v_2} \]zvanou zákon lomu. Tuto argumentaci lze použít i pro elektromagnetické vlny (světlo) – více podrobností k lomu světla najdete v kapitole 23.
Zdroj
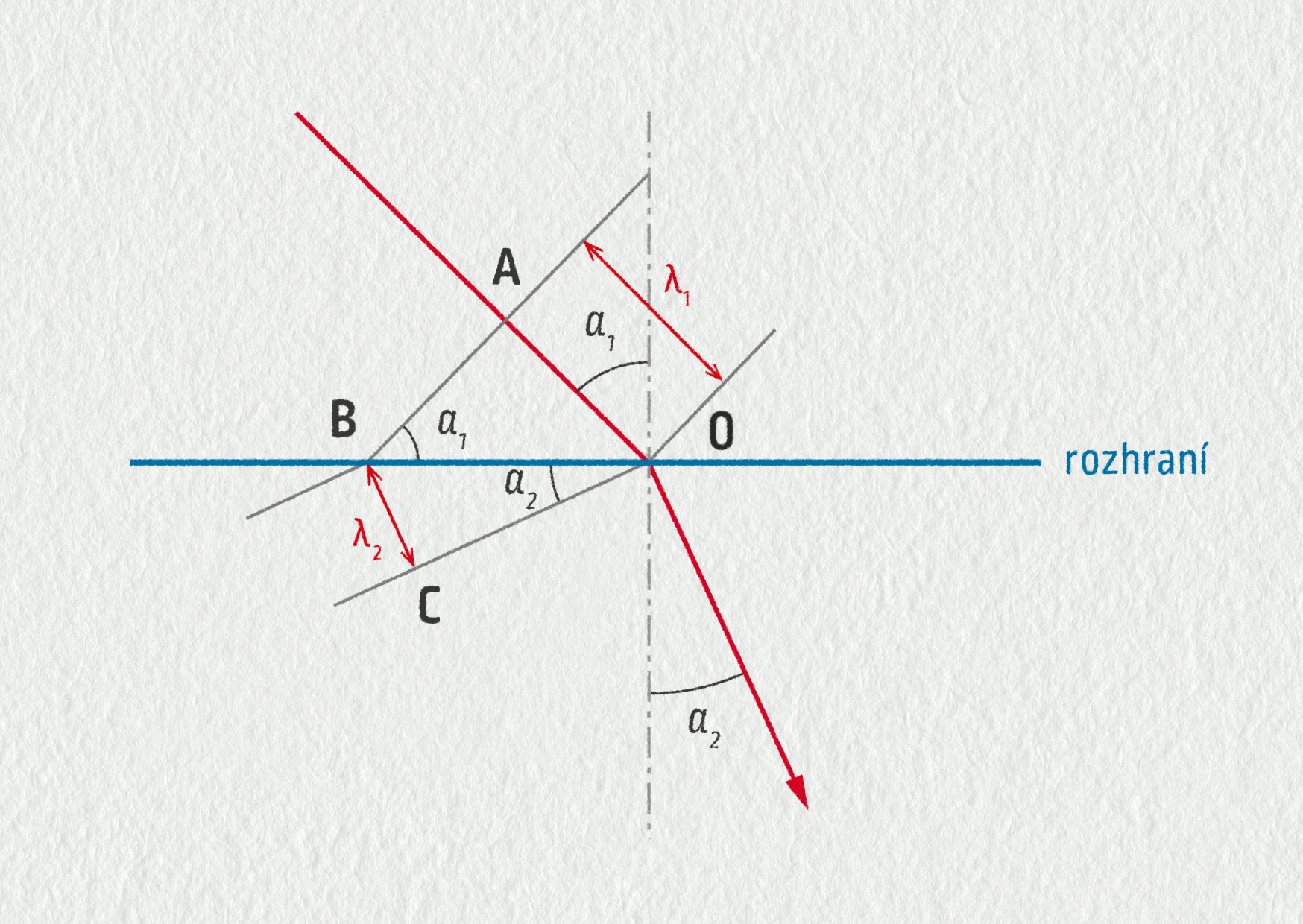
Zákon lomu jednoduše odvodíme z podmínky spojitosti vlnoploch na rozhraní – viz obrázek 22.35. V pravoúhlém trojúhelníku OAB platí
\[ \sin\alpha_1 = \frac{|OA|}{|OB|} = \frac{\lambda_1}{|OB|}\;. \]Podobně v pravoúhlém trojúhelníku OBC platí
\[ \sin\alpha_2 = \frac{|BC|}{|OB|} = \frac{\lambda_2}{|OB|}\;. \]Vydělením těchto rovnic zjišťujeme, že
\[ \frac{\sin\alpha_1}{\sin\alpha_2} = \frac{\lambda_1}{\lambda_2} \]Vlnová délka souvisí s rychlostí šíření vztahem \(\lambda=v/f\), přičemž frekvence vlnění je nad i pod rozhraním stejná. Odsud již získáváme vyjádření zákona lomu pomocí rychlostí šíření vln v prostředích
\[ \frac{\sin\alpha_1}{\sin\alpha_2} = \frac{v_1}{v_2}\;. \]Dopplerův jev
Dalším zajímavým jevem typickým pro vlnění je Dopplerův jev. Popsán byl už v roce 1842 Christianem Dopplerem, profesorem matematiky na pražské technice. Pozorovatelný je jak pro mechanické, tak elektromagnetické vlny. Spočívá ve změně frekvence vlnění, pokud se vůči sobě zdroj vlnění a přijímač pohybují:
- frekvence vlnění zaregistrovaná přijímačem \(f_\mathrm{P}\) je větší než frekvence zdroje \(f_\mathrm{Z}\), pokud se vzájemně přibližují,
- frekvence vlnění zaregistrovaná přijímačem \(f_\mathrm{P}\) je menší než frekvence zdroje \(f_\mathrm{Z}\), pokud se vzájemně vzdalují.
Pokud se zdroj a přijímač vůči sobě nepohybují, frekvence \(f_\mathrm{P}\) a \(f_\mathrm{Z}\) jsou stejné.
Dopplerův jev můžete dobře pozorovat, nebo lépe řečeno poslouchat, když zastavíte na odpočívadle u dálnice. Kolem vás projíždějí stálou rychlostí jiná auta (jejich motor má konstantní otáčky a vydává zvuk určité výšky). Když se k vám přibližují, slyšíte vyšší tón (vyšší frekvenci). Jakmile vás minou a začnou se vzdalovat, slyšíte nižší tón (nižší frekvenci). Čím je vyšší rychlost přibližování nebo vzdalování, tím je Dopplerův efekt výraznější. Seznámit se s ním můžete i v následujícím videu z Velké ceny Kanady F1.
Dopplerův jev v praxi

Zdroj

Zdroj
Zdroj
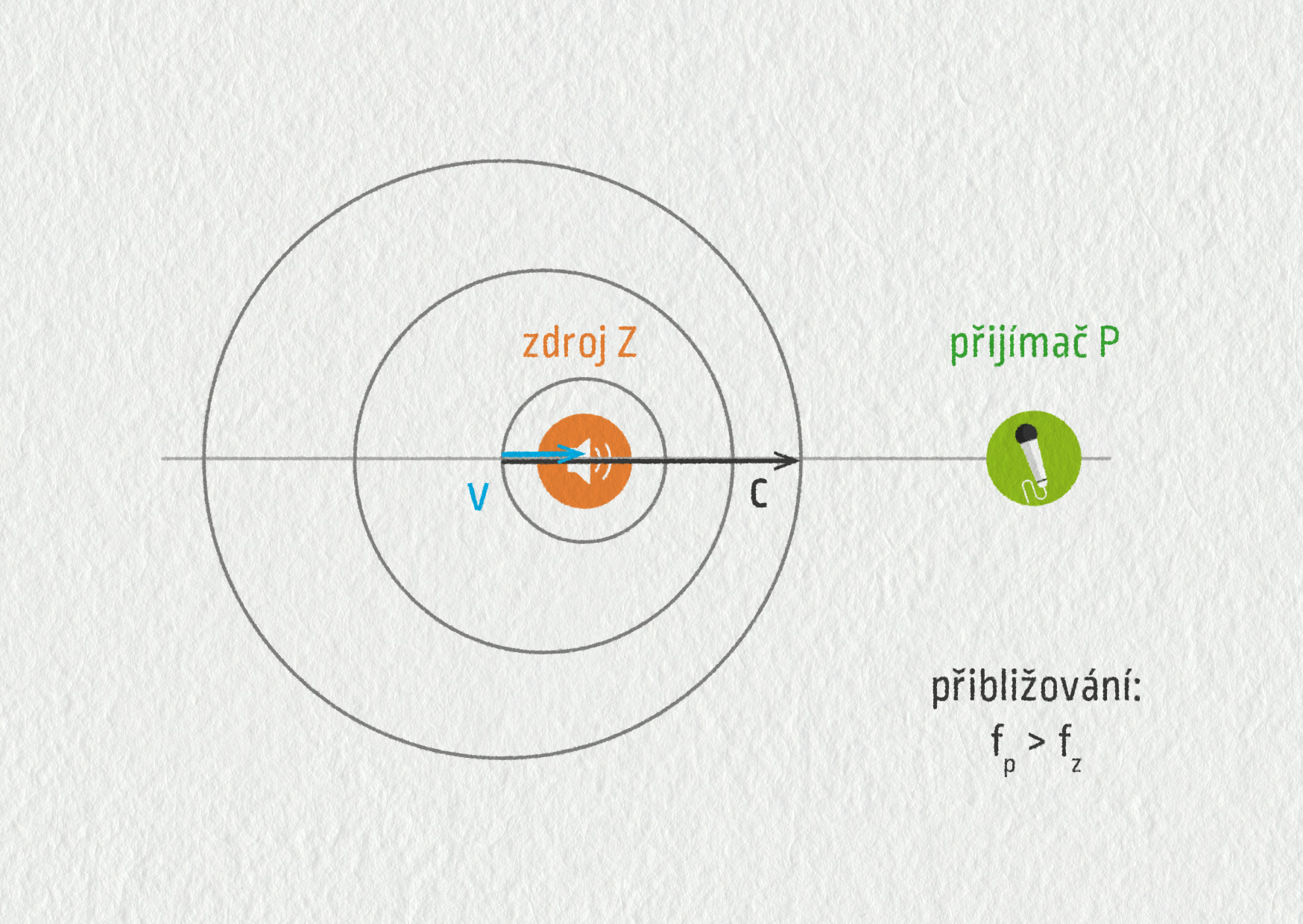
Prozkoumáme nyní podrobněji Dopplerův jev pro šíření zvuku ve vzduchu. Předpokládejme, že zdroj zvuku Z kmitá s frekvencí fZ a pohybuje se vůči okolnímu vzduchu rychlostí v směrem k přijímači. Přijímač P nechť je v klidu vůči vzduchu. Rychlost šíření zvuku ve vzduchu označíme písmenem \(c\). Situace je znázorněna na obrázku 22.37. Jakou frekvenci zvuku \(f_\mathrm{P}\) zaregistruje přijímač?
Zdroj
Pro přibližování zdroje k přijímači platí
\[ f_\mathrm{P} = \frac c{c-v} f_\mathrm{Z}\;. \]Pro vzdalování zdroje od přijímače platí
\[ f_\mathrm{P} = \frac c{c+v} f_\mathrm{Z}\;. \]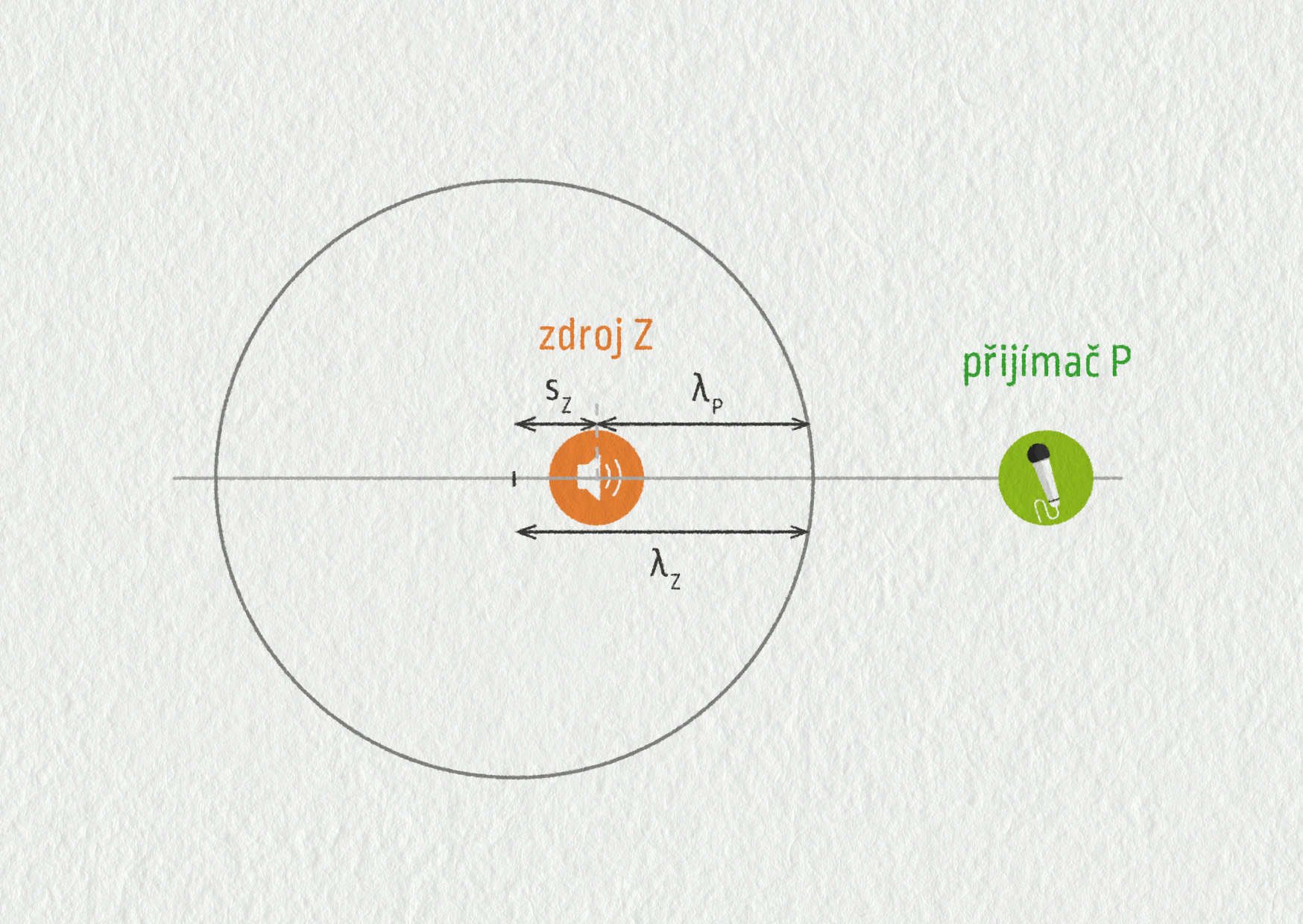
Zdroj
Za dobu, kdy zdroj kmitne jedenkrát (perioda \(T_\mathrm{Z}\)), urazí zvukové vlnění vzdálenost \(\lambda_\mathrm{Z}=cT_\mathrm{Z}\) a zdroj samotný se přiblíží k přijímači o vzdálenost \(s_\mathrm{Z}=vT_\mathrm{Z}\). Vlnová délka zaznamenaná přijímačem je podle obrázku 22.38 \(\lambda_\mathrm{P}=\lambda_\mathrm{Z}-s_\mathrm{Z}\), takže po dosazení získáme
\[ \lambda_\mathrm{P} = cT_\mathrm{Z} - vT_\mathrm{Z} = (c-v)T_\mathrm{Z} = \frac{c-v}{f_\mathrm{Z}}\;. \]Vlnovou délku zaznamenanou přijímačem můžeme vyjádřit také jako \(\lambda_\mathrm{P}=c/f_\mathrm{P}\). Porovnáním předchozích vztahů dostáváme souvislost mezi frekvencemi
\[ \frac{c}{f_\mathrm{P}} = \frac{c-v}{f_\mathrm{Z}} \quad\hbox{neboli}\quad f_\mathrm{P} = \frac c{c-v} f_\mathrm{Z}\;. \]Lokomotiva projíždí pod mostem rychlostí 90 km/h a píšťalou vydává zvuk o frekvenci 1 000 Hz. Jakou frekvenci uslyší pozorovatel na mostě?

Zdroj
Rychlost zdroje zvuku vůči pozorovateli je \(v=90\ \mathrm{km/h}=25\ \mathrm{m/s}\).
Frekvence zdroje zvuku je \(f_\mathrm{Z}=1000\ \mathrm{Hz}\).
Nemáme přesnou informaci o teplotě vzduchu, ale podle fotografie lokomotivy a zejména podle vegetace v pozadí snímku můžeme usoudit, že teplota vzduchu nebude příliš vzdálená od 15 °C, čemuž odpovídá rychlost zvuku přibližně \(c=340\ \mathrm{m/s}\).
Během přibližování vlaku uslyší pozorovatel tón o frekvenci
\[ f_{\mathrm{P}1} = \frac{340}{340-25}\cdot1000\ \mathrm{Hz} \approx 1080\ \mathrm{Hz}\;, \]během vzdalování vlaku pak tón o frekvenci
\[ f_{\mathrm{P}2} = \frac{340}{340+25}\cdot1000\ \mathrm{Hz} \approx 932\ \mathrm{Hz}\;. \]Poznamenejme, že tato změna frekvence je dobře slyšitelná – jde o více jak jeden celý tón.
Ohyb vlnění
Ohyb vlnění, nazývaný též difrakce, spočívá v deformaci vlnoploch překážkami. Díky ohybu mohou vlny částečně proniknout i za překážku, do oblastí geometrického stínu. Platí, že čím je velikost překážky bližší vlnové délce, tím je ohyb výraznější. Difrakce se uplatňuje jak u mechanických, tak u elektromagnetických vln – viz kapitola Vlnová optika.


Zdroj
Interference vlnění
Snad nejzajímavějším a nejtypičtějším projevem vlnové povahy je interference. Interferencí se rozumí skládání vlnění z více zdrojů v určité oblasti prostoru. Matematicky je to pouhé sčítání okamžitých výchylek vln, které dospěly do vybraného bodu.
Dvě vlny, které se „potkají“ v určitém místě, se mohou interferenčně zesilovat, takže prostředí v tomto bodě bude kmitat s velkou amplitudou. Ale mohou se také interferenčně zeslabovat, takže prostředí v tomto bodě nekmitá vůbec, přestože do tohoto místa směřují obě vlny. Sčítání dvou sinusových vln stejné frekvence si můžete vyzkoušet v animaci – prozkoumejte, jaký vliv na výslednou vlnu má amplituda a počáteční fáze jednotlivých vln.

Zdroj
Interferovat mohou pochopitelně pouze vlny stejné povahy (zvuková se zvukovou, elektromagnetická s elektromagnetickou atp.). Jak uvidíme v kapitole 24, interference má obrovský význam v optice a moderní fyzice. Pokud jde o zvuk, neméně podstatné interferenční jevy vznikají v hudebních nástrojích. Na tomto místě se pokusíme o základní pochopení problematiky interference.
Zdroj
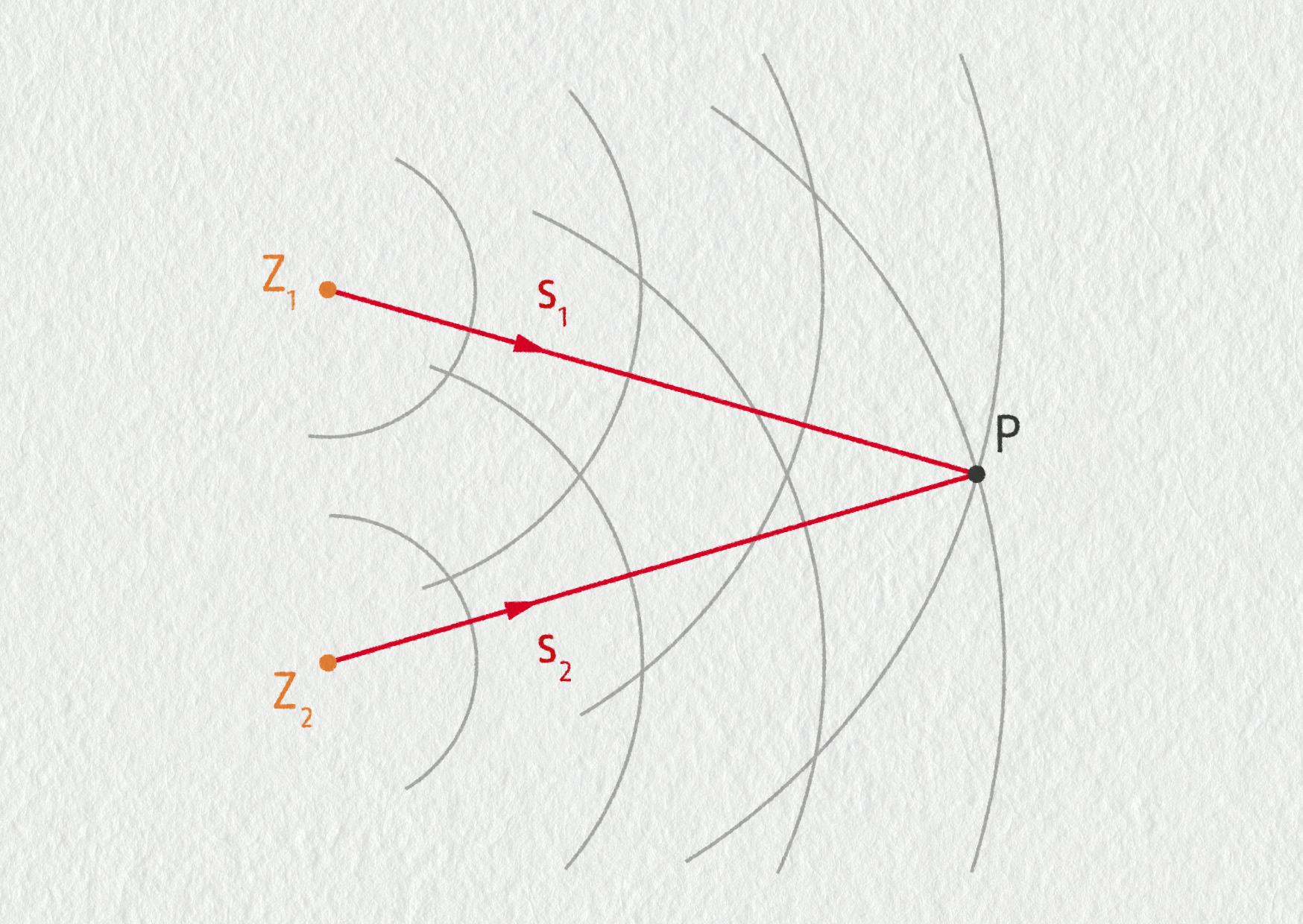
Uvažujme dva zdroje Z1 a Z2, které kmitají se stejnou frekvencí a zcela synchronizovaně (ve fázi). Vytvořené vlny se prolínají v určité oblasti prostoru – viz obrázek 22.42. Bod P ležící v tomto interferenčním poli se nachází ve vzdálenosti \(s_1\) od zdroje Z1 a ve vzdálenosti \(s_2\) od zdroje Z2. V bodě P nastává právě jedna z následujících možností:
- Vlny do bodu P dospěly se stejnou fází, jejich amplitudy se sčítají, nastává konstruktivní interference. Prostředí v bodě P kmitá s maximální amplitudou. Aby obě vlny měly v bodě P stejnou fázi, musí být rozdíl mezi uraženými dráhami celočíselným násobkem vlnové délky. Podmínka konstruktivní interference se zapisuje matematicky jako \(|s_1-s_2|=k\lambda\), kde \(k=0,1,2,3,\dots\)
- Vlny do bodu P dospěly s opačnou fází, jejich amplitudy se odečítají, nastává destruktivní interference. Prostředí v bodě P kmitá s minimální amplitudou. Aby obě vlny měly v bodě P opačnou fázi, musí být rozdíl mezi uraženými dráhami poločíselným násobkem vlnové délky. Podmínka destruktivní interference se zapisuje matematicky jako \(|s_1-s_2|=\lambda/2+k\lambda\), kde \(k=0,1,2,3,\dots\)
- Vlny do bodu P dospějí s jiným fázovým posuvem než v předchozích případech. Vlny se opět skládají a amplituda kmitání prostředí v bodě P není ani maximální, ani minimální – jedná se o přechodový stav mezi první a druhou možností.

Zdroj
Interference má nepřeberné množství aplikací, my si zde ukažme jednu zajímavou s mechanickými vlnami. Ke zkvalitnění poslechového vjemu využívají bezdrátová sluchátka technologie ANC (Active Noise Control, aktivní potlačení hluku). Princip založený na destruktivní interferenci byl patentován před více jak 90 lety. Sluchátka jsou opatřena miniaturním mikrofonem, který snímá rušivé zvuky přicházející z okolí. Do reproduktoru (vedle přehrávané skladby) pouští zvuky o stejné amplitudě a frekvenci, ale s opačnou fází, takže ruchy přicházející z okolí destruktivně interferují s ruchy generovanými reproduktorem a tím se dosahuje nerušeného poslechu přehrávané skladby. U moderních sluchátek je možno úroveň potlačení hluku nastavovat, aby posluchač částečně vnímal případná nebezpečí např. v městském provozu.

Zdroj
Poměrně častým a pozoruhodným příkladem interference je skládání dvou postupných vln, které postupují po přímce proti sobě. Výsledkem je zvláštní druh vlnění, kterému říkáme stojaté vlnění. Nejčastěji se s ním setkáme u prostředí, která jsou prostorově omezená (tyč, struna, deska) – v tomto případě vlna přímá interferuje s vlnou odraženou na okraji tělesa. Situaci pro strunu a vzduchový sloupec uvnitř píšťaly podrobněji rozebereme v oddílu věnovaném hudebním nástrojům.

Zdroj
Prozkoumáme podrobněji interferenci dvou protichůdných vln o stejné frekvenci a amplitudě. Vlna A nechť se šíří v kladném směru osy \(x\). Její rovnice je
\[ y_A = y_\mathrm{m}\sin\left[2\pi\left(\frac tT-\frac x{\lambda}\right)\right]\;. \]Vlna B nechť postupuje v opačném směru, v rovnici se to projeví změnou znaménka
\[ y_B = y_\mathrm{m}\sin\left[2\pi\left(\frac tT+\frac x{\lambda}\right)\right]\;. \]Rovnici popisující kmitání prostředí v bodě o souřadnici \(x\), kde se vlny překrývají, získáme prostým součtem výchylek:
\[\begin{aligned} y=y_A+y_B &= y_\mathrm{m}\sin\left[2\pi\left(\frac tT-\frac x{\lambda}\right)\right] + y_\mathrm{m}\sin\left[2\pi\left(\frac tT+\frac x{\lambda}\right)\right]\\ &= y_\mathrm{m}\left\{\sin\left[2\pi\left(\frac tT-\frac x{\lambda}\right)\right] + \sin\left[2\pi\left(\frac tT+\frac x{\lambda}\right)\right]\right\}\\ \end{aligned}\]Ve složené závorce sčítáme siny dvou různých argumentů, pro které platí trigonometrický vzorec
\[ \sin a + \sin b = 2\sin\left(\frac{a+b}2\right)\cos\left(\frac{a-b}2\right)\;. \]Po dosazení a úpravě
\[ y = 2y_\mathrm{m}\sin\left[\frac{\displaystyle2\pi\left(\frac tT-\frac x\lambda\right)+2\pi\left(\frac tT+\frac x\lambda\right)}2\right] \cos\left[\frac{\displaystyle2\pi\left(\frac tT-\frac x\lambda\right)-2\pi\left(\frac tT+\frac x\lambda\right)}2\right] = \] \[ = 2y_\mathrm{m}\sin\left(\frac{2\pi t}T\right)\cos\left(\frac{2\pi x}\lambda\right) \]získáváme rovnici stojaté vlny
\[ y = \left[2y_\mathrm{m}\cos\left(\frac{2\pi t}T\right)\right]\sin\left(\frac{2\pi x}\lambda\right) \]Všimněte si, že stojatá vlna má stejnou periodu (a frekvenci) jako interferující vlny. Členy v hranaté závorce nezávisí na čase, a představují tedy amplitudu kmitání prostředí v bodě o souřadnici \(x\).
Pozoruhodné je, že stojatá vlna nepostupuje v prostoru. V prostředí existují místa, která kmitají s maximální amplitudou, nazývaná kmitny. V našem výpočtu to jsou body, pro něž je kosinus maximální (buď 1 nebo −1), čili \(x=k\lambda/2\), kde \(k\) je celé číslo. Existují zde rovněž místa, která nekmitají vůbec, přestože se jimi trvale šíří obě protichůdné vlny. Tato místa se nazývají uzly stojatého vlnění. V našem výpočtu jsou to body, pro něž je kosinus roven nule, tedy \(x=\lambda/4+k\lambda/2\), kde \(k\) je opět celé číslo. Vzdálenost dvou sousedních kmiten (a též vzdálenost dvou sousedních uzlů) je rovna polovině vlnové délky interferujících vln.

Zdroj

Zdroj
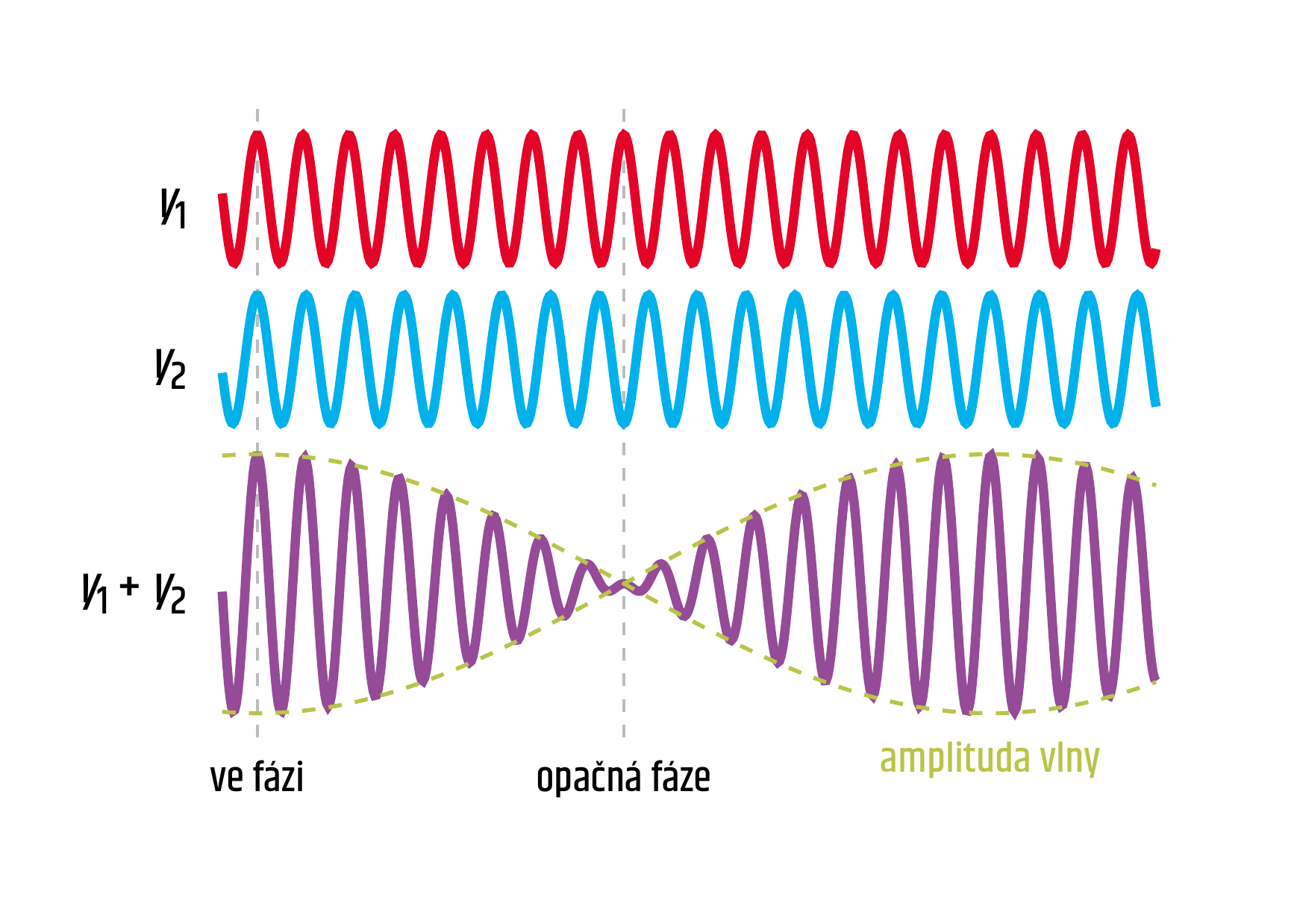
Skládání dvou vln o různých frekvencích si můžete prohlédnout v animaci.
Zdroj
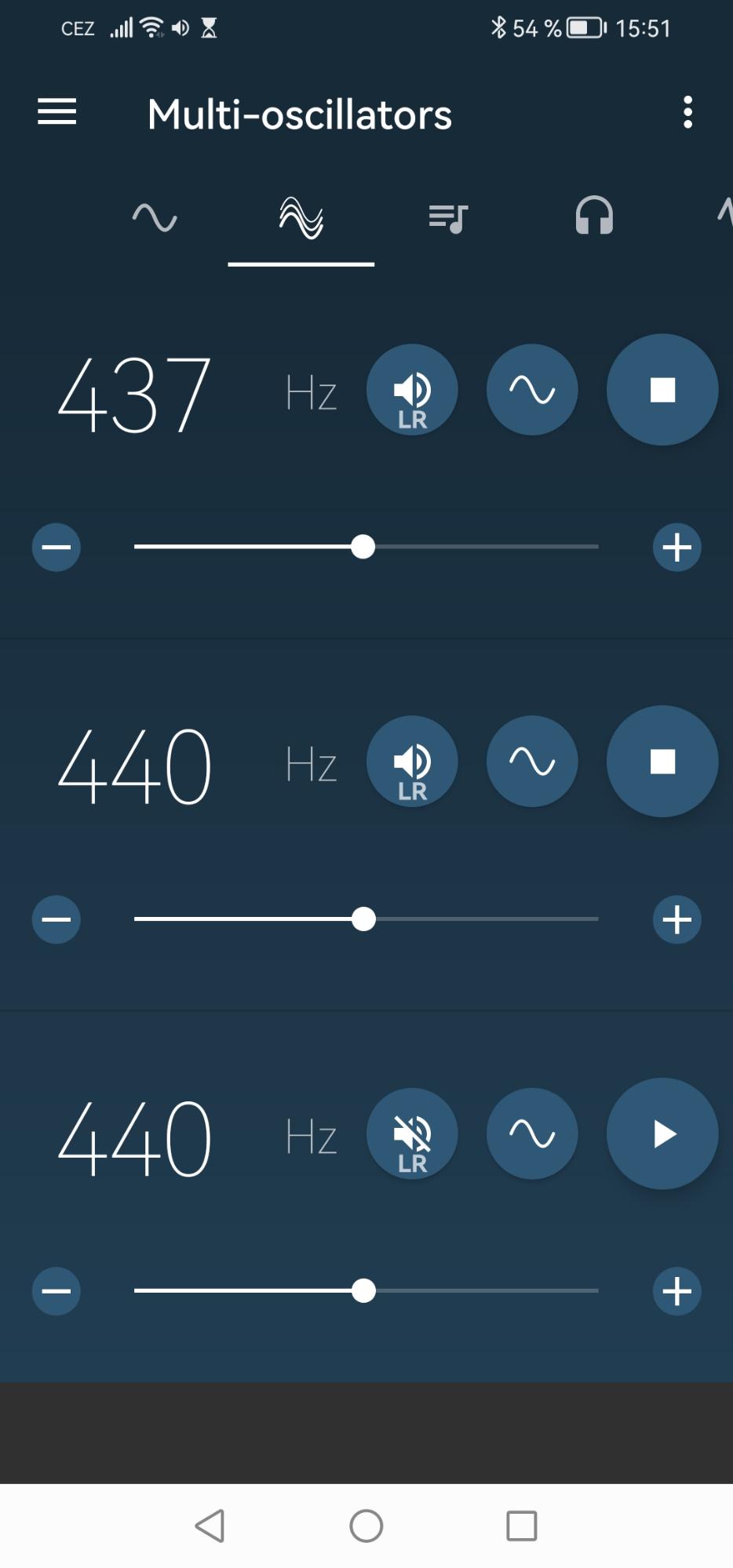
Fyzikálně zajímavý výsledek dostaneme, když frekvence těchto vln – označíme je \(f_1\) a \(f_2\) – jsou blízké. Jev je dobře postřehnutelný u zvukových vln a je znám pod pojmem rázy. Výsledné vlnění má frekvenci rovnou aritmetickému průměru frekvencí složek \((f_1+f_2)/2\) a amplituda slyšitelného zvuku pulzuje s frekvencí danou rozdílem frekvencí \(|f_1-f_2|\).
Zdroj

