V předchozí části jsme používali časové závislosti x(t), v(t), tedy funkce popisující časový vývoj sledovaných veličin. Teď budeme hledat předpisy pro funkce popisující některé jednoduché druhy pohybu. Proč se hledáním předpisů vůbec zabývat? Umožní nám mnohem elegantnější řešení úloh o pohybu a také lepší porozumění jednotlivým druhům pohybů. A v neposlední řadě také předvídat chování tělesa.
Jak popsat rovnoměrný pohyb?
Rovnoměrný pohyb znamená pohyb stále stejně velkou rychlostí. V případě pohybu v prostoru se může měnit směr rychlosti, například auto může zatáčet, přesto velikost rychlosti může být stálá – jde stále o rovnoměrný pohyb. To je vše, co potřebujeme vědět, zbytek si snadno odvodíme sami pomocí tohoto příkladu:
Chodec vyráží z polohy x0 = 10 m a pohybuje se stálou rychlostí 2 m/s ve směru osy x. Nakreslete graf x(t).
Zdroj
Rychlost 2 m/s znamená, že po uplynutí 1 s se pohne o 2 m. Jeho poloha se tím změní z x = 10 m na x = 12 m, atd. To můžeme znázornit v grafu takto:
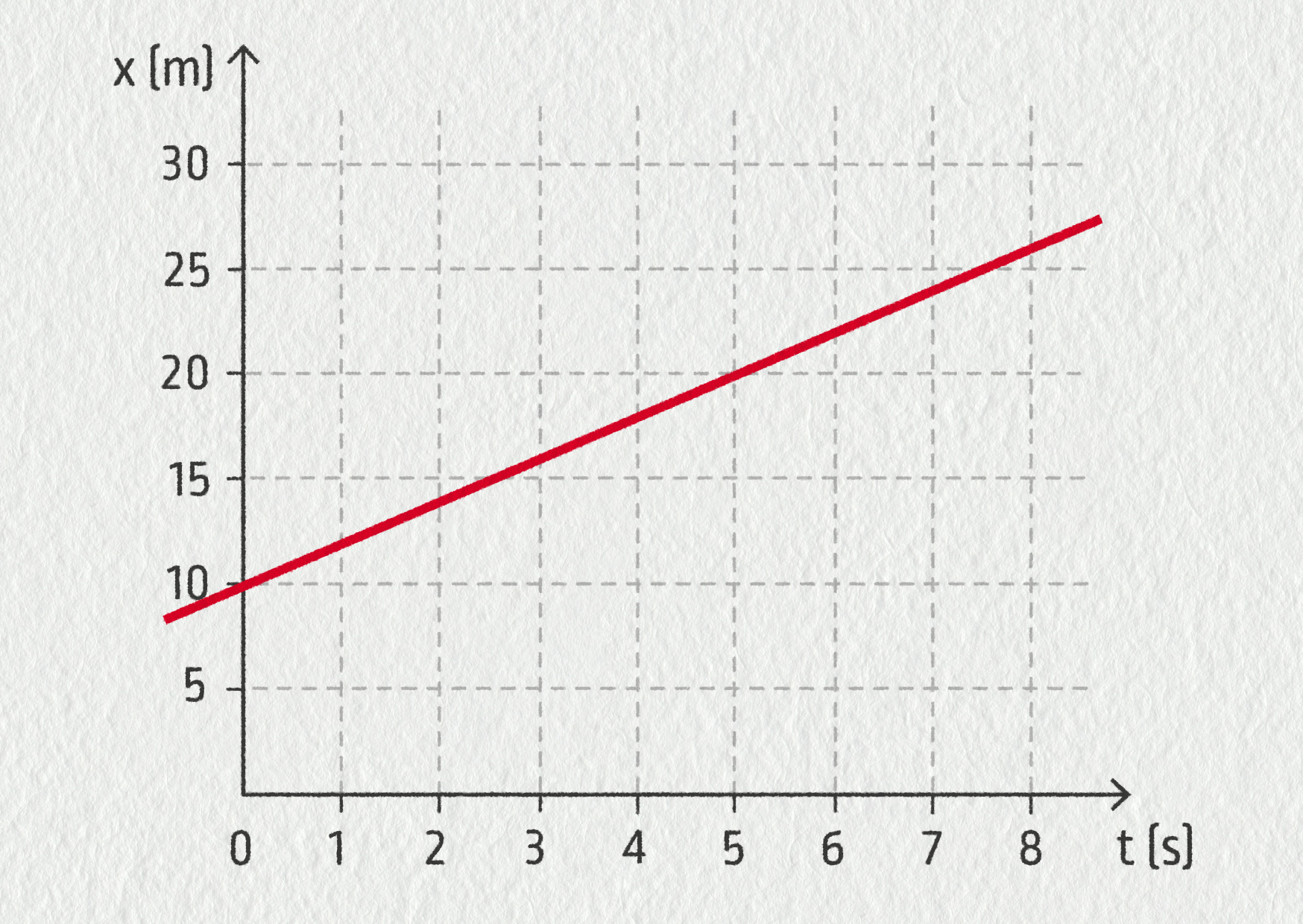
Zdroj
Tento výsledek představuje lineární funkci a můžeme ho zobecnit pro libovolný rovnoměrný pohyb.
- \(x(t) = vt + x_0\), kde x0 je počáteční poloha a v je neměnná rychlost pohybu.
- \(v(t) = v = \mathrm{konst.}\)

Zdroj
Všimněte si podobnosti se vzorcem s = vt, neboť dráha s je u přímočarého pohybu vzdálenost mezi počáteční a aktuální polohou (\(s = x(t) - x_0\)). Počáteční poloha hraje roli zejména při pohybu dvou a více těles, jak ukazuje následující úloha o pohybu.
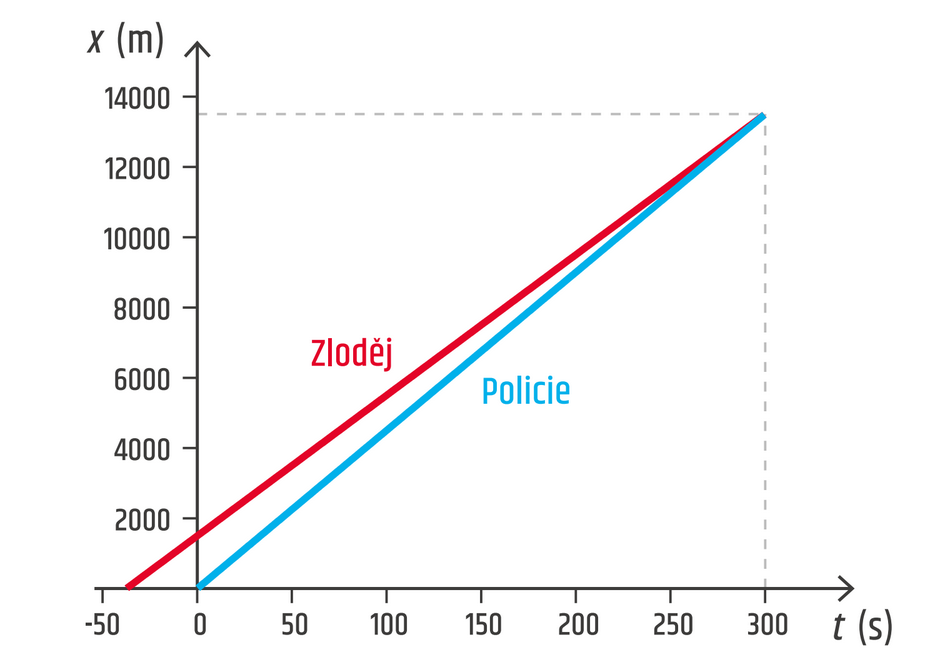
Polohu obou aut můžeme popsat pomocí funkcí x(t), kdy osa x bude začínat v místě činu a čas nula bude odpovídat okamžiku, kdy z místa činu vyjelo policejní auto:
Zloděj: \(x_1(t) = v_1t+x_1\), kde v1 = 40 m/s a x1 = 1500 m.
Policie: \(x_2(t) = v_2t\), kde v2 = 45 m/s.
K setkání dojde v takovém okamžiku, kdy \(x_1(t) = x_2(t)\). Proto \[ \begin{aligned} v_1t + x_1 &= v_2t\\ x_1 &= v_2t - v_1t\\ x_1 &= (v_2-v_1)t\\ t &= \frac{x_1}{v_2-v_1}\\ t &= 300\ \mathrm{s}\\ \end{aligned} \]Pro výpočet polohy setkání můžeme zvolit jak policii, tak zloděje. Jejich polohy musí být stejné, což nám poslouží jako kontrola správnosti: \(x_2(t) = v_2t = 13\,500\ \mathrm{m}\), \(x_1(t)=v_1t+x_1=13\,500\ \mathrm{m}\).
Závěr: Policie dohoní zloděje za 300 s ve vzdálenosti 13 500 m od místa činu.
Zdroj
Jak popsat rovnoměrně zrychlený pohyb?
Rovnoměrně zrychlený pohyb je pohyb se stálým zrychlením. To znamená, že rychlost se mění, ale poměr Δv/Δt zůstává stále stejný. Pokud těleso zpomaluje, mluvíme o rovnoměrně zpomaleném pohybu. Názornou představu o rovnoměrně zrychleném pohybu nám dá příklad padajícího kamene.
Kámen padá se stálým zrychlením a = g = 10 m/s2. Načrtněte grafy x(t), v(t) pro tento pohyb. Tip: začněte od rychlosti, polohu si nechte na konec. Začneme tedy od rychlosti. Zrychlení 10 m/s2 znamená, že za 1 s se rychlost zvětší o 10 m/s, za další 1 s o dalších 10 m/s, atd. To můžeme znázornit v grafu takto:

Zdroj
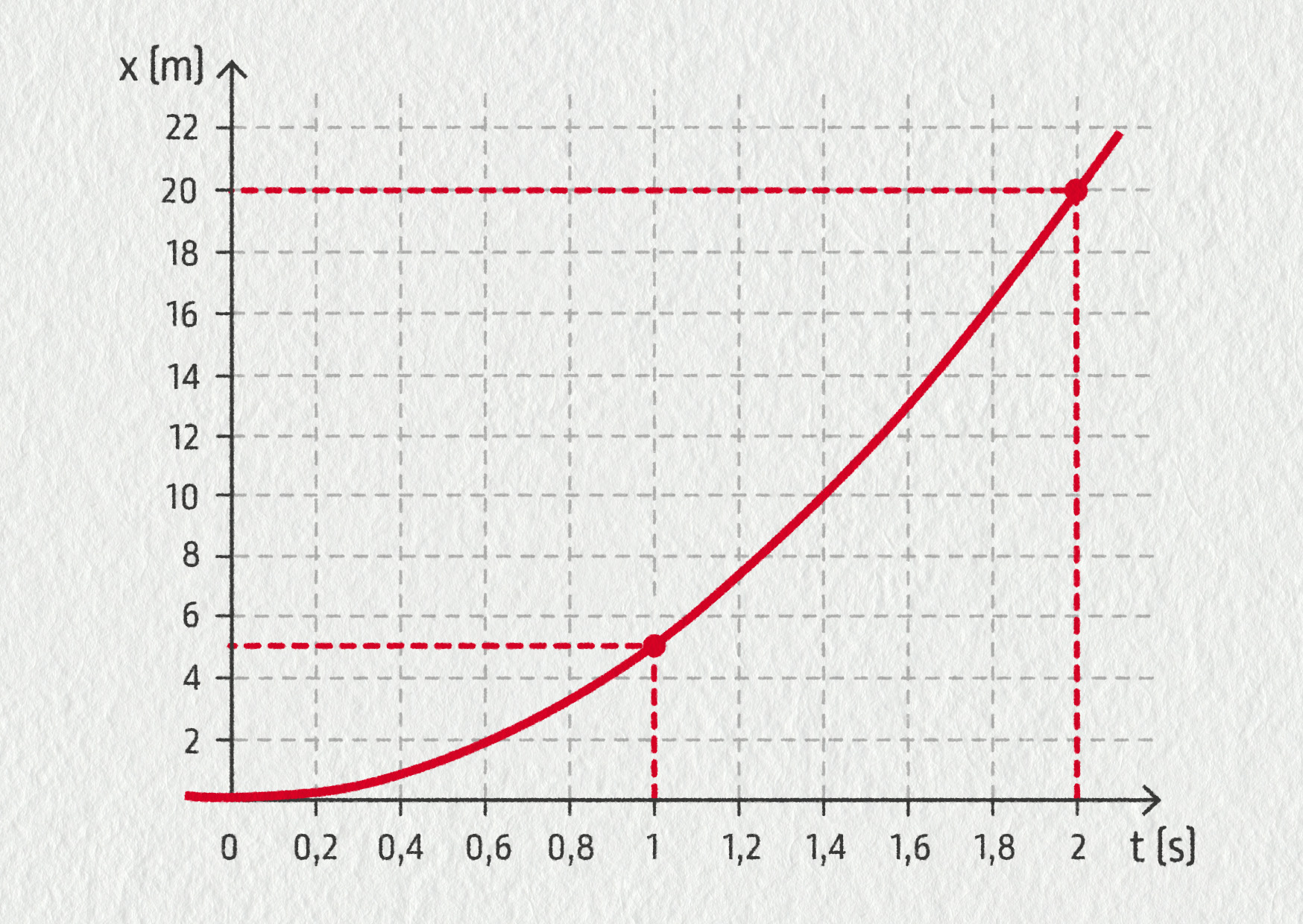
Nyní se podíváme na polohu. Už víme, že je možné ji určit z grafu rychlosti jako obsah plochy pod křivkou. V našem případě padajícího kamene plochu spočítáme snadno jako obsah pravoúhlého trojúhelníku (viz obrázek). Například v čase t = 1s je plocha 0,5 ⋅ 1s ⋅ 10m/s = 5 m. V čase 2 s už je to 0,5 ⋅ 2s ⋅ 20m/s = 20 m, atd. Po dopočítání několika dalších hodnot vidíme, že křivka není „rovná”, možná v ní někteří poznáváte parabolu.
Zdroj
Právě jsme vyřešili rovnoměrně zrychlený pohyb v jeho jednoduché podobě s nulovou počáteční rychlostí a polohou. V grafech můžeme nalézt i předpisy funkcí:
Pro jednoduchý rovnoměrně zrychlený pohyb s nulovou počáteční rychlostí i polohou platí:
Pro rychlost \(\displaystyle v(t) = at\) (lineární funkce).
Pro polohu \(\displaystyle x(t) = \frac{1}{2} at^2\) (kvadratická funkce).
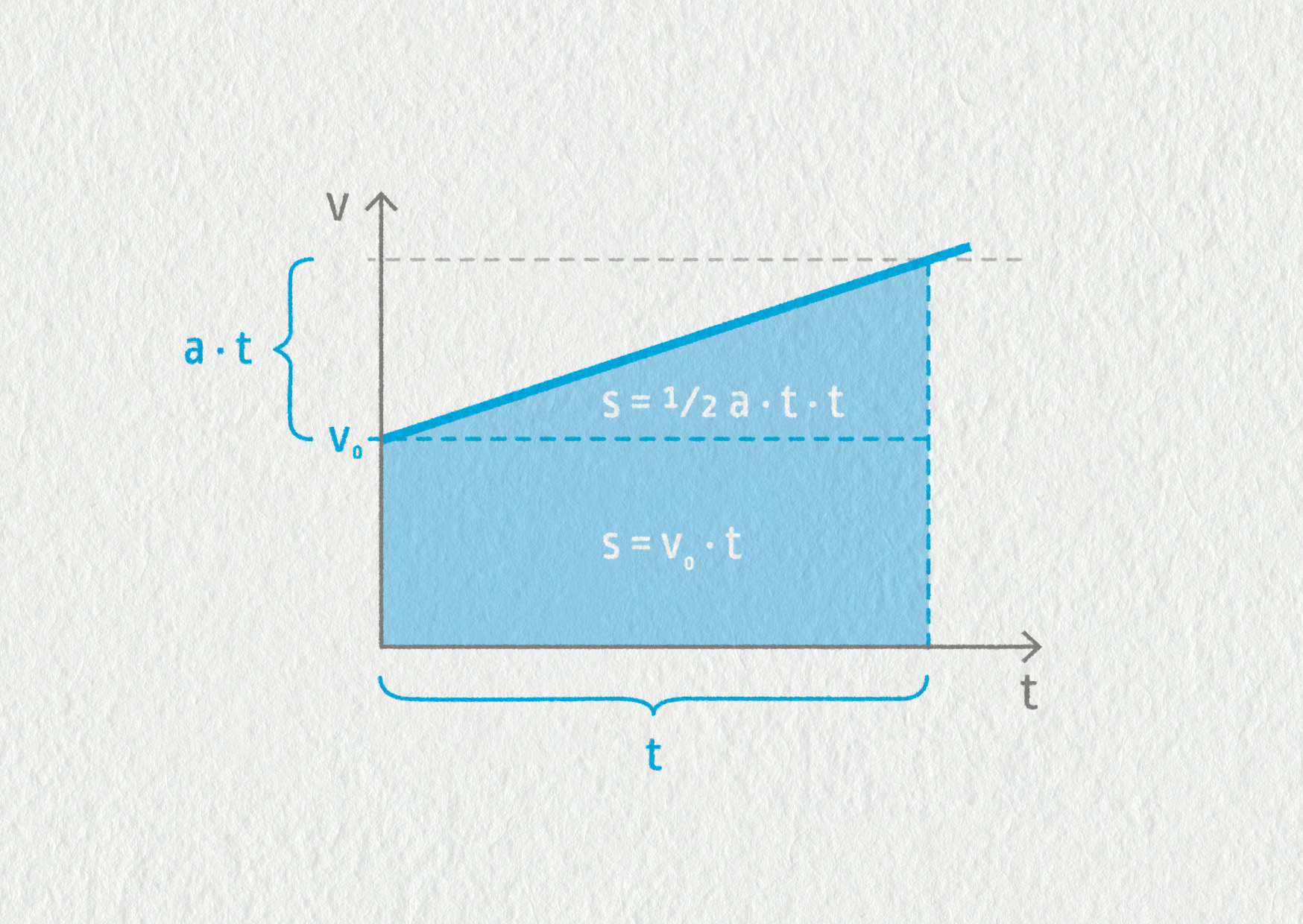
Jak by se situace změnila, pokud by byl kámen vržen svisle počáteční rychlostí v0 z počáteční polohy x0? Ke zrychlenému pohybu se jednoduše „přičte” ještě pohyb rovnoměrný (viz obrázek),
Zdroj
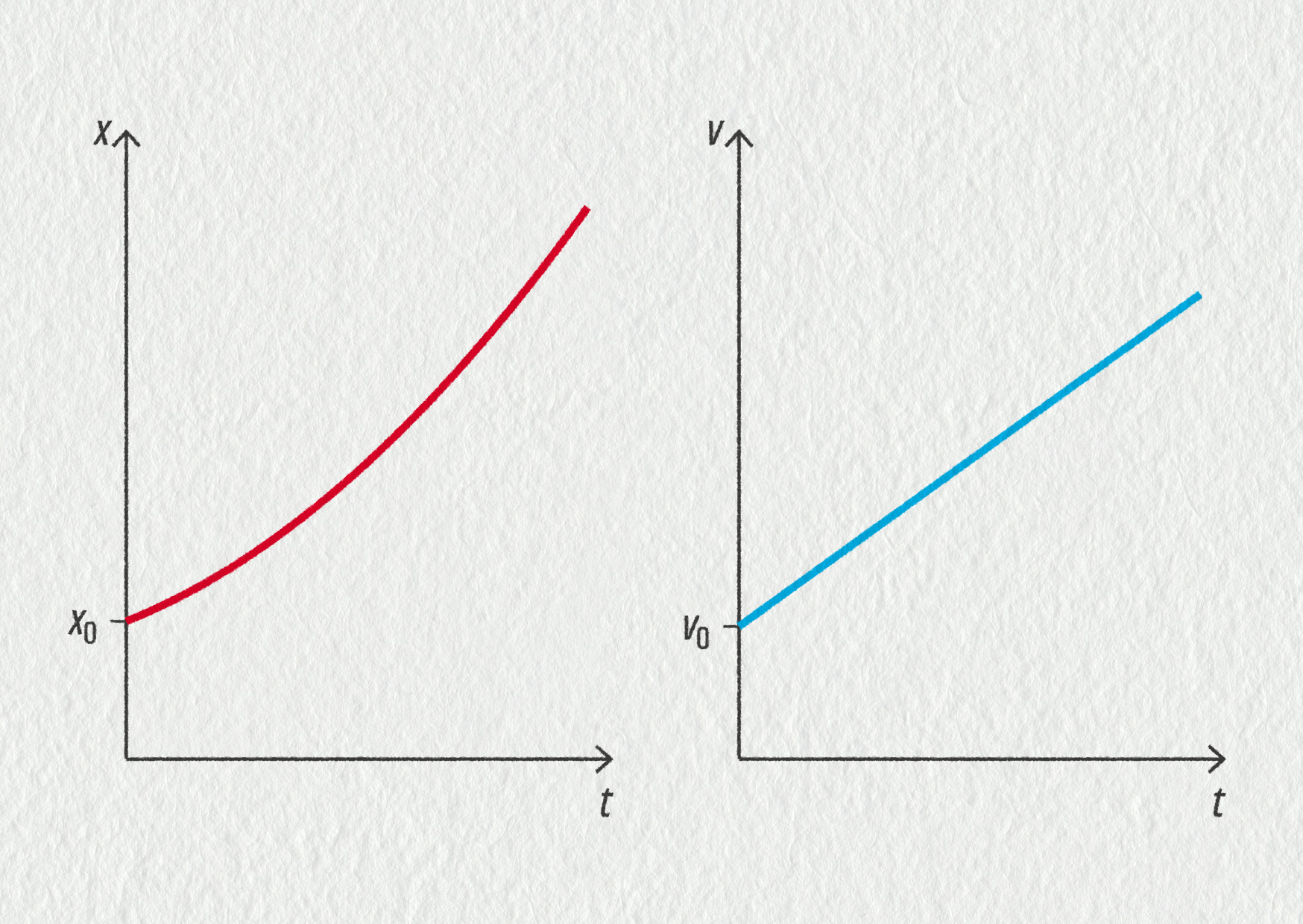
a dostaneme obecné předpisy:
Při rovnoměrně zrychleném pohybu platí:
Pro rychlost \(\displaystyle v(t) = at + v_0\), kde v0 je počáteční rychlost, a je neměnné zrychlení.
Pro polohu \(\displaystyle x(t) = \frac{1}{2} at^2 + v_0t + x_0\), kde x0 je počáteční poloha, v0 je počáteční rychlost.
Zdroj
Závislost polohy na čase obsahuje druhou mocninu t, takové funkci říkáme kvadratická a jejím grafem je vždy část paraboly. Můžete si sami snadno ověřit, že pokud dosadíte a = 0, dostanete funkce pro rovnoměrný pohyb. Vliv zrychlení a počáteční rychlosti na podobu grafů můžete prozkoumat v appletu a procvičit v následujících úlohách.
Vlak se nachází na trati v poloze x0 = 1 500 m a jeho rychlost je v0 = 90 km/h ve směru osy x. V tomto místě začíná zrychlovat se zrychlením a = 2 m/s2 až na rychlost 180 km/h. Načrtněte grafy x(t), v(t) pro tento pohyb. Napište také předpisy uvedených funkcí.
Rychlost musíme převést na m/s: v0 = 90 km/h = 25 m/s, v1 = 180 km/h = 50 m/s. Teď zbývá dosadit:
Poloha: \(\displaystyle x(t) = \frac{1}{2} at^2 + v_0t + x_0\) \(\displaystyle = 1t^2 + 25t + 1500\ (\mathrm{m})\)
Rychlost: \(v(t) = at + v_0 = 2t + 25\ (\mathrm{m/s})\)
Pokud se těleso pohybuje ve směru osy x, ale brzdí, jedná se o speciální případ rovnoměrně zrychleného pohybu. Platí stejné vzorce, jen zrychlení musíme opatřit záporným znaménkem.
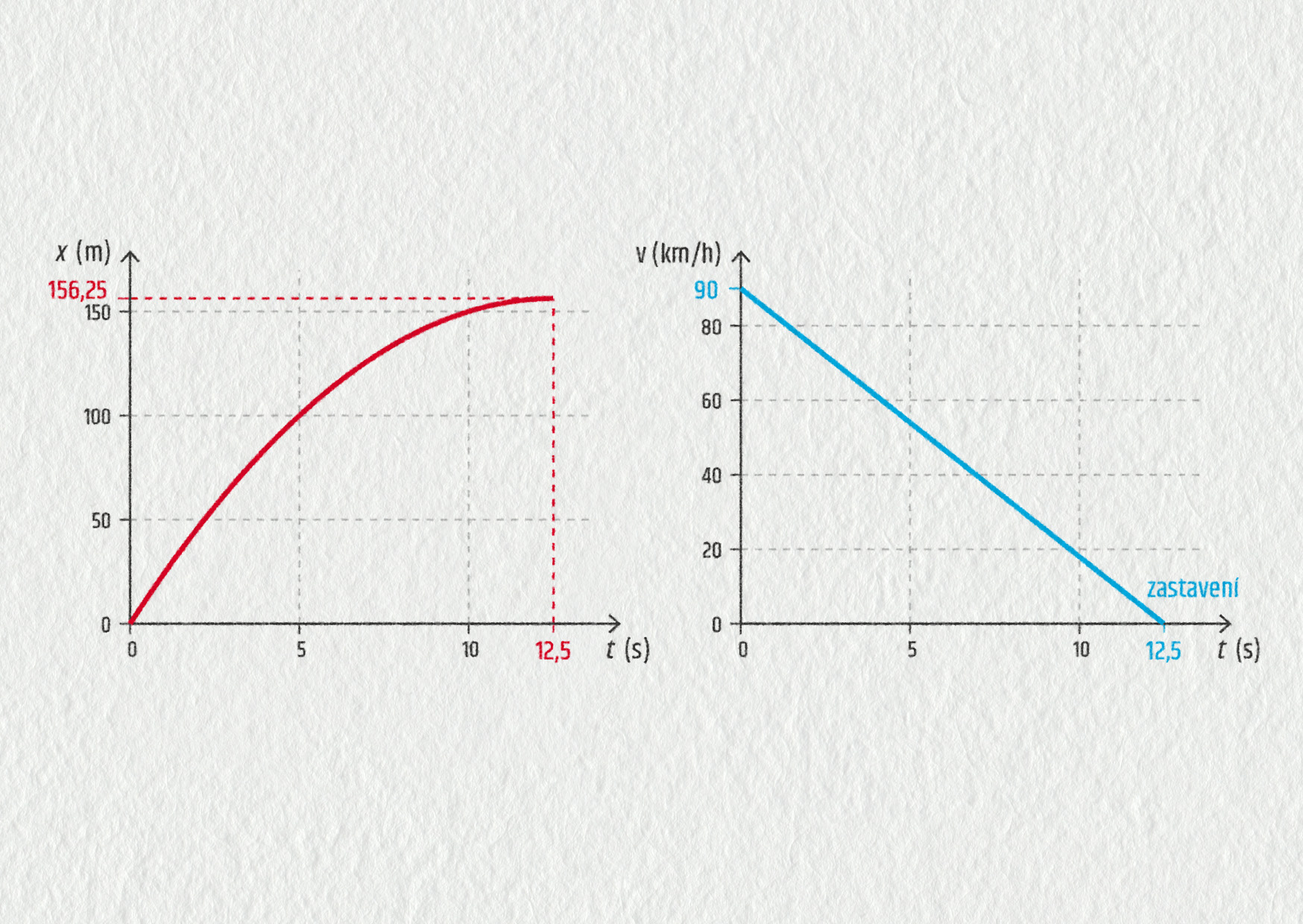
Auto jede rychlostí v0 = 90 km/h a brzdí se zrychlením a = 2 m/s2 až do zastavení. Načrtněte grafy x(t), v(t) pro tento pohyb.
Ještě připomeňme, že složitější druhy pohybu, kdy se zrychlení mění, dokážeme také popsat, ale jen pomocí grafů. Předpisy těchto funkcí určit v tuto chvíli nedokážeme. Co se týče rovnoměrně zrychleného pohybu, zbývá nám vyřešit ještě pár důležitých příkladů. První z nich je drobnou modifikací úlohy o padajícím kameni. Pohyb zůstává stejný, mění se jen známé a neznámé veličiny.
- Kámen padá se zrychlením a = g = 10 m/s2 z výšky 15 m. Za jak dlouho a jakou rychlostí dopadne?
- Kámen padal se zrychlením a = g = 10 m/s2. Bylo změřeno, že za 1,2 s dopadnul. Z jaké výšky padal?
- Kámen volně upuštěný na neznámé planetě dopadl z výšky 10 m rychlostí 8,6 m/s. Jaké je na planetě zrychlení?
a) Zvolíme osu x s počátkem v původní poloze kamene (15 m nad zemí) orientovanou směrem dolů. Pro polohu kamene pak platí \(x(t) = \frac{1}{2} gt^2\). V okamžiku dopadu musí platit: \(x(t) = h = 15\ \mathrm{m}\). Proto \(h = \frac{1}{2} gt^2\), a odtud
\(\displaystyle t = \sqrt{\frac{2g}{h}}\) \(t = 1{,}73\ \mathrm{s}\).
Rychlost kamene bude: \(v(t) = gt = 17{,}3\ \mathrm{m/s}\).
b) Situace je stejná jako v předchozí variantě, změnila se pouze neznámá. Do vztahu \(h = \frac{1}{2}gt^2\) můžeme přímo dosazovat: h = 7,2 m.
c) Opět podobná situace, tentokrát neznáme zrychlení a ani čas, známe výšku h a rychlost v. Ze vzorce \(v = at\) proto musíme vyjádřit neznámou t a dosadit do druhého vztahu: \(\displaystyle h = \frac{1}{2}at^2 = \frac{1}{2}a\left(\frac{v}{a}\right)^{\!2} = \frac{1}{2}\frac{v^2}{a}\).
Teprve teď můžeme vyjádřit neznámou a: \(\displaystyle a = \frac{v^2}{2h} = 3{,}7\ \mathrm{m/s^2}\).
Vypočítejte brzdnou dráhu auta, které jede rychlostí 90 km/h, za následujících podmínek: reakční doba řidiče je 0,5 s. (Reakční doba je čas od spatření překážky do sešlápnutí brzdy.) Zrychlení auta při prudkém brždění na suché silnici je 5 m/s2 (předpokládáme rovnoměrně zpomalený pohyb). Sledovaný úsek silnice má délku 850 m. Doplňte také grafy v(t) a x(t).
Brzdná dráha se bude skládat ze dvou částí. Nejdřív auto 0,5 s jede stálou rychlostí 90 km/h = 25 m/s. Přitom urazí dráhu \(s_1 = v_1t_1 = 12{,}5\ \mathrm{m}\).
Potom auto brzdí se zrychlením 5 m/s2, dokud nezastaví. Pro zrychlení platí \(a = \Delta v/\Delta t\), odtud \(\Delta t = \Delta v/a = 5\ \mathrm{s}\), označíme si tento čas jako t2 = 5 s. Uražená dráha při zpomalování bude \(s_2 = v_1t_2 - \frac{1}{2} at^2 = 62{,}5\ \mathrm{m}\).
Celková brzdná dráha je \(s = s_1 + s_2 = 75\ \mathrm{m}\).
Nakonec tu máme opět úlohu o pohybu dvou těles, tentokrát se zpomalujícím rychlíkem. Úlohu vyřešíme pomocí kvadratické rovnice a taky pomocí počítače, který nám pomůže vykreslit grafy funkcí.
Strojvůdce rychlíku jedoucího rychlostí 108 km/h spatří před sebou ve vzdálenosti 180 m nákladní vlak jedoucí stejným směrem rychlostí 32,4 km/h. Rychlík začne brzdit se zrychlením o velikosti 1,2 m/s2. Dojde ke srážce?
Rychlík: \(x_\mathrm{R} = v_\mathrm{R}t - \frac{1}{2}at^2 \), kde vR = 108 km/h = 30 m/s.
Nákladní vlak: \(x_\mathrm{N} = x_0 + v_\mathrm{N}t \), kde x0 = 180 m a vN = 32,4 km/h = 9 m/s.
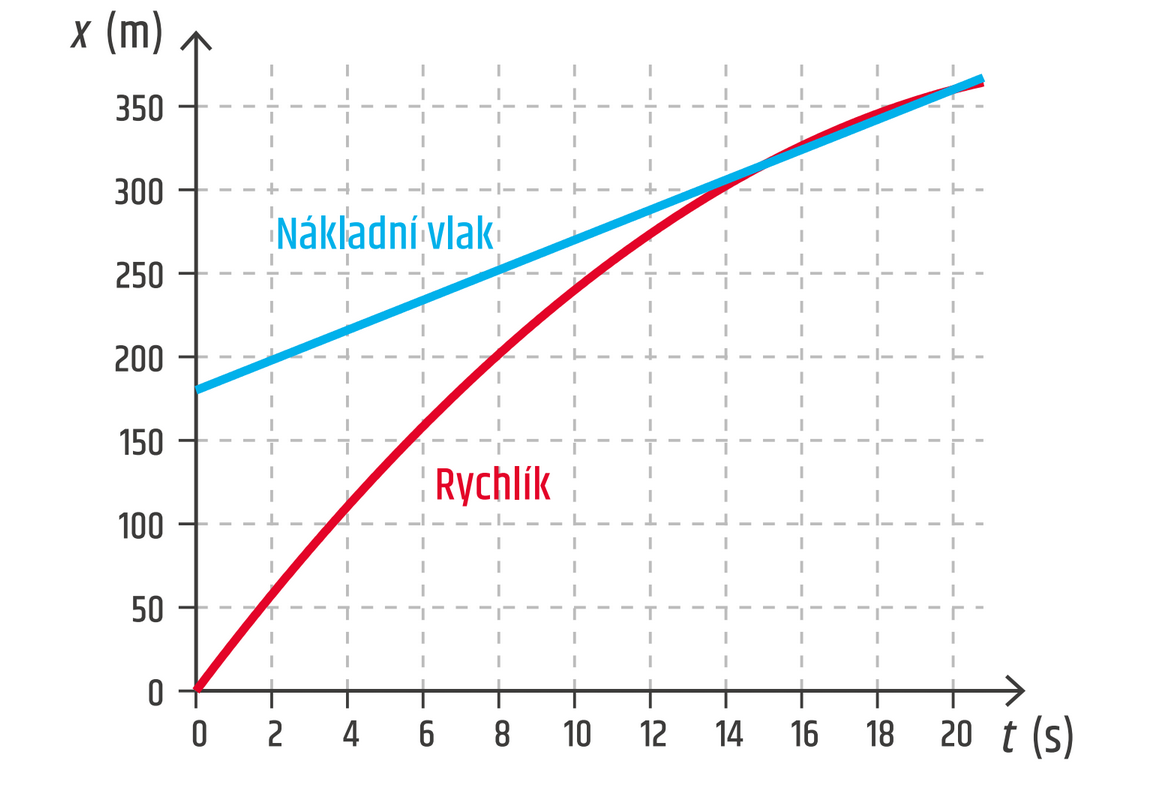
Grafické řešení: Vykreslíme
xR = 30t − 0,6t2 (m)
xN = 180 + 9t (m)
Zdroj
Početní řešení: xR = xN
30t − 0,6t2 = 180 − 9t
0,6t2 − 21t + 180 = 0
Rovnice má dvě řešení t1 = 15 s, t2 = 20 s.
Závěr: Ke srážce dojde za 15 s.