K popisu pohybu hmotného bodu nám nestačí měřit jeho polohu nebo uraženou dráhu. Potřebujeme ještě zjistit, jak dlouho pohyb trval. Kombinací dráhy a času dostáváme rychlost pohybu. Nejprve si připomeňme průměrnou rychlost vp:
Průměrná rychlost je podíl uražené dráhy s a doby pohybu t.
Jednotkou rychlosti v soustavě SI je m ⋅ s−1. Kromě toho často používáme také km/h. Platí 1 m ⋅ s−1 = 3,6 km ⋅ h−1, neboť: \(\displaystyle 1\ \mathrm{m}\cdot\mathrm{s}^{-1}\) \(\displaystyle = \frac{1/1000\ \mathrm{km}}{1/3600\ \mathrm{h}}\) \(\displaystyle = \frac{3600}{1000}\ \mathrm{km}\cdot\mathrm{h}^{-1}\) \(\displaystyle = 3{,}6\ \mathrm{km}\cdot\mathrm{h}^{-1}\)
| Příklady rychlostí | |
|---|---|
| pohyb africké desky směrem k Evropě cca | 5 cm/rok |
| klidná chůze | 4 km/h |
| vytrvalostní běh (rekreační) | 10 km/h |
| sprint 100 m | 36 km/h |
| gepard ve sprintu | 90 km/h |
| vítr v hurikánu (stupeň 5) | 250 km/h |
| dopravní letadlo (běžná rychlost) | 900 km/h |
| zvuk ve vzduchu | 1 200 km/h |
| sonda Voyager II | 60 000 km/h |
| oběh Země kolem Slunce | 100 000 km/h |
| světlo ve vakuu* | 1 080 000 000 km/h |
V praxi se občas potkáte i s jinými jednotkami rychlosti:
mph = 0,44704 m/s – mile per hour (míle za hodinu), používá se v USA
uzel = 0,51444 m/s – anglicky knot = námořní míle za hodinu, používá se v letectví a mořeplavbě
Určete průměrné rychlosti v m/s:
V následujících úlohách si ukážeme, že průměrná rychlost není průměr rychlostí. Je to vždy celková dráha za celkový čas.
- První část: s1 = 10 km, v1 = 10 km/h.
- Druhá část: s2 = 10 km, v2 = 30 km/h.
Průměrná rychlost je celková dráha za celkový čas. Celková dráha je \(s = s_1 + s_2 = 20\ \mathrm{km}\). Celkový čas t spočítáme jako součet časů t1 a t2:
\[t_1 = s_1/v_1\] \[t_2 = s_2/v_1\] \[ t = t_1 + t_2 = \] \[= s_1/v_1 + s_2/v_1 = 4/3\nobreakspace \mathrm{h} \]Celková průměrná rychlost je pak:
\[v = s/t = 15\nobreakspace \mathrm{km/h} \]Označme vzdálenost z A do B jako s = 10 km. Průměrná rychlost je celková dráha za celkový čas: \[v = \frac{2s}{t}\] Odtud celkový čas \(t = 2s/v = 1\ \mathrm{h}\). Podívejme se teď na cestu tam: doba jízdy je \(t_1 = s/v_1 = 1\ \mathrm{h}\). To ovšem znamená, že ať pojede jakoukoliv rychlostí, tak celkové průměrné rychlosti 20 km/h už nedosáhne.
Při určování rychlosti musíme mít na paměti, že rychlost je relativní veličina – vždy záleží na volbě vztažné soustavy. Například čtenář tohoto odstavce je právě v klidu vzhledem k zemskému povrchu (nečte-li třeba ve vlaku). Přitom vůči Slunci se pohybuje rychlostí kolem 30 000 m/s.
Jak definujeme okamžitou rychlost?
Průměrná rychlost charakterizuje pohyb jako celek na určitém úseku, ale neříká vůbec nic o jednotlivých fázích pohybu. Představme si to na příkladu jízdy autem z Brna do Prahy. Délka trasy po dálnici je 210 km, doba jízdy byla 2 hodiny. Průměrná rychlost tedy vychází 105 km/h, ale o průběhu cesty nevíme nic bližšího. Přesto se řidič v libovolném okamžiku své cesty mohl podívat na tachometr a zjistit, jakou rychlostí jede „právě teď” neboli určit svoji okamžitou rychlost.
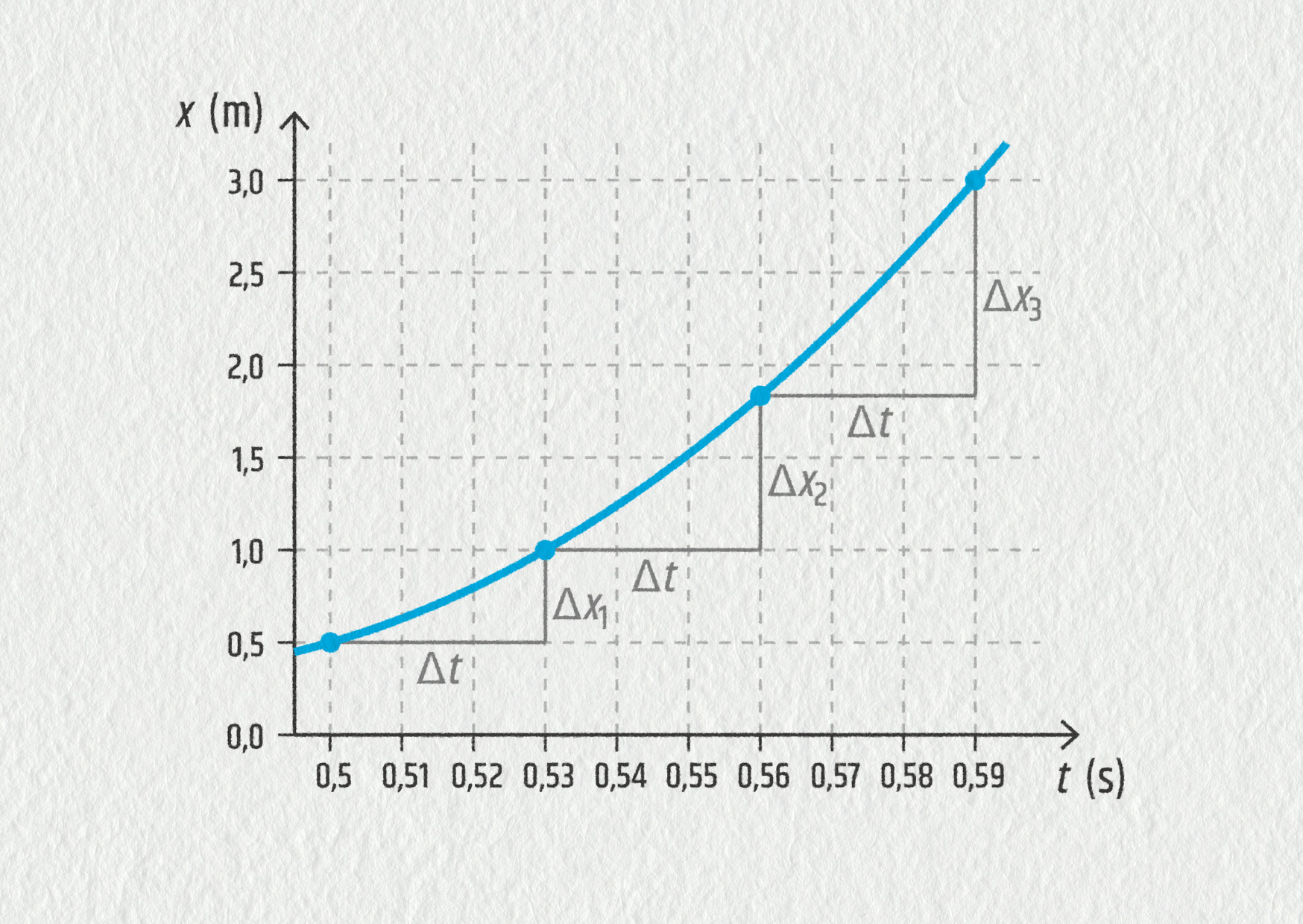
Chtěli bychom definovat veličinu, která bude charakterizovat pohyb tělesa v určitém okamžiku, a to včetně směru jeho pohybu. Jak to můžeme udělat? Může nám k tomu pomoci záznam polohy v závislosti na čase. Podívejme se detailně na rozjezd autíčka v grafu x(t):
Zdroj

Zdroj
Okamžitou rychlost určíme pomocí dvou blízkých bodů ve zvoleném místě grafu (Δt je nejmenší možné).
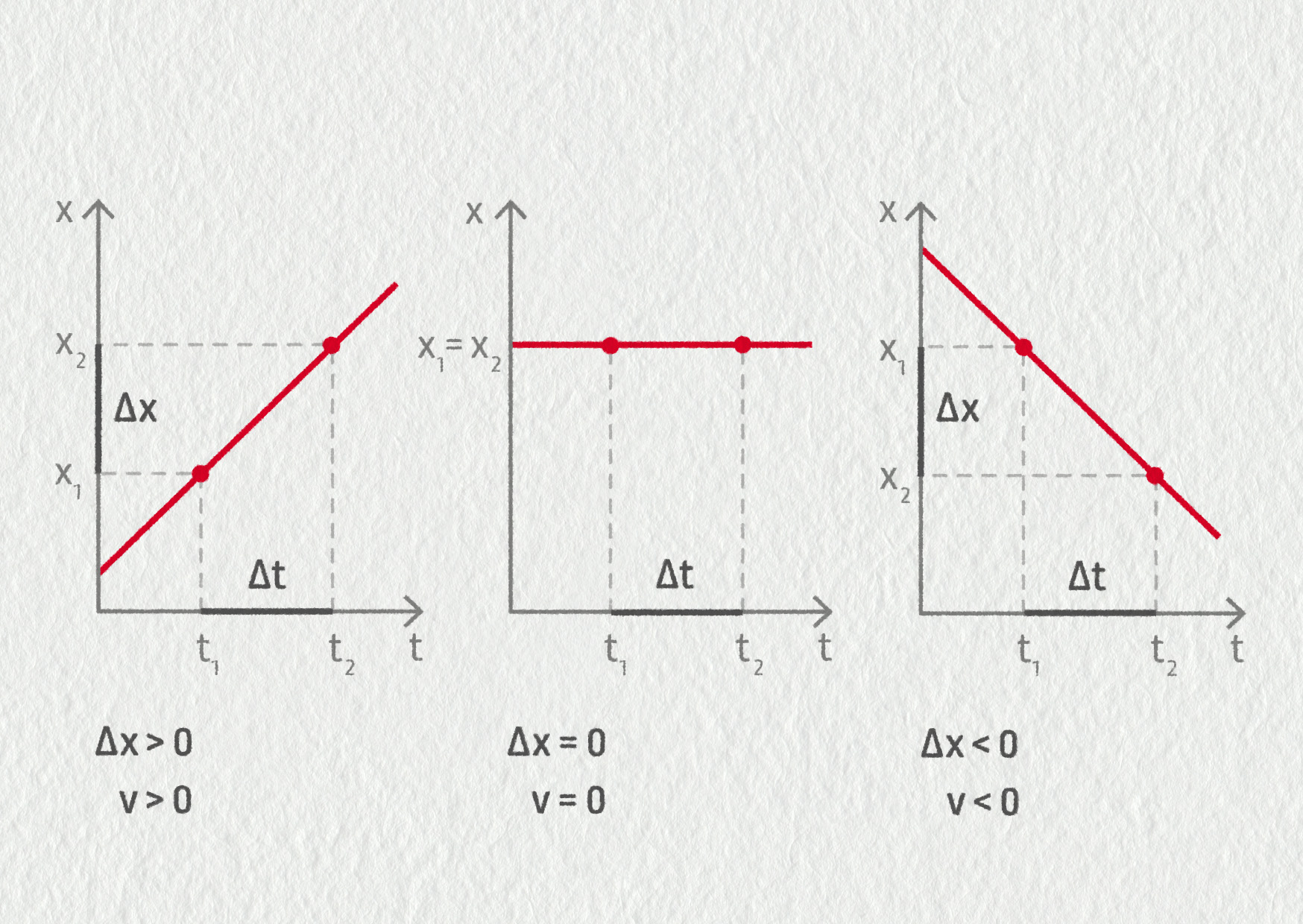
Symbol Δ (delta) se ve fyzice používá pro rozdíl hodnot dané veličiny (\(\Delta x=x_2-x_1\)). Okamžitá rychlost, na rozdíl od průměrné rychlosti, nese i informaci o směru pohybu. Jelikož se pohybujeme jen na jedné ose, má směr pohybu pouze dvě možnosti, které rozlišíme pomocí znaménka (viz obrázek). Indexem x u rychlosti dáváme najevo, že jde o rychlost ve směru osy x. Pokud nehrozí záměna s jinými souřadnicemi (celá tato kapitola), můžeme malé x klidně vynechávat. Definici rychlosti v prostoru najdete v kapitole 14.
Zdroj
Pozorný čtenář by správně namítnul, že název „okamžitá“ v naší definici rychlosti není zcela na místě, neboť definice se vztahuje k určitému časovému intervalu. Prakticky vzato můžeme zvýšením frekvence snímání sonaru časový interval Δt zkrátit. Nikdy ale nebudeme schopni změřit rychlost v jediném okamžiku. Matematici si s tímto problémem umějí poradit pomocí na první pohled velmi podivného pojmu – nekonečně malého časového intervalu dt. Tento pojem stál u zrodu celého nového oboru matematiky na konci 17. století – infinitezimálního počtu. Pro fyziku je podstatné, že něco jako okamžitá rychlost existuje – autíčko se nepohybuje „skoky“ v prostoru, ale spojitě. Uvedená definice se pojmu okamžité rychlosti může přiblížit s libovolnou přesností.
Jak definujeme zrychlení?
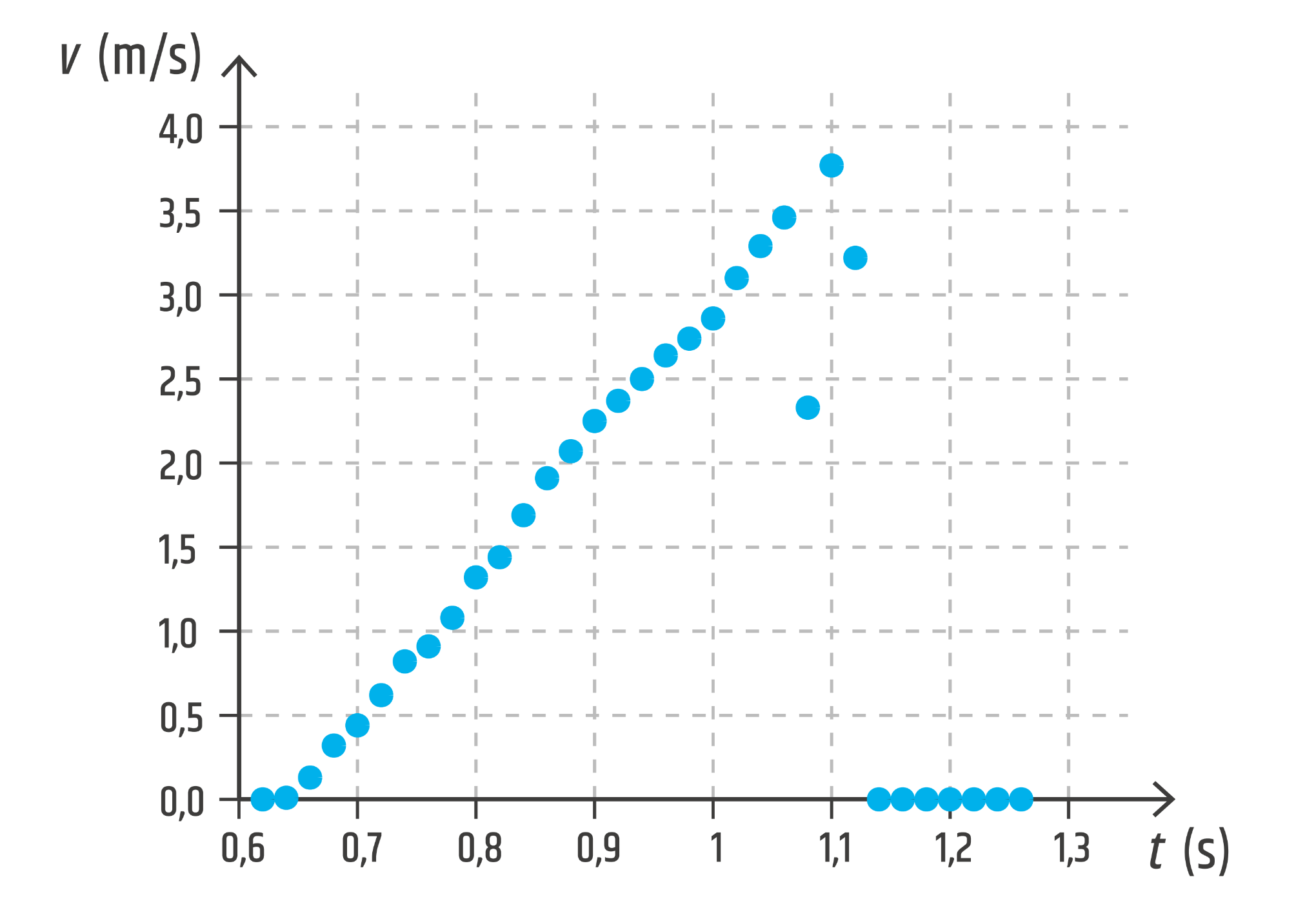
Okamžitá rychlost se během pohybu může měnit. Dobře je to vidět na padajícím tělese. Asi nikoho nepřekvapí, že při svém pádu zrychluje. Můžeme to ostatně změřit pomocí sonaru a míče (viz obrázek). Podívejte se na časové závislosti polohy a rychlosti míče během pádu.

Zdroj
Zdroj
Zrychlení definujeme podobně jako okamžitou rychlost, sledujeme změnu rychlosti \(\Delta v=v_2-v_1\) v časovém intervalu \(\Delta t=t_2-t_1\). V našem grafu vidíme, že rychlost rostla docela rovnoměrně – asi o 1 m/s za každou desetinu sekundy. To znamená asi o 10 m/s za jednu sekundu.
Základní jednotkou je m/s/s = m/s2 = m ⋅ s−2 (čteme „metr za sekundu na druhou“ nebo „metr sekunda na mínus druhou“).

Zdroj
Podobně jako u rychlosti můžeme i u zrychlení přímočarých pohybů index x v této kapitole vynechávat. Analogický je i vztah mezi průměrným a okamžitým zrychlením: v případě okamžitého zrychlení musí být Δt co nejmenší, u průměrného zrychlení označuje Δt celkovou dobu zrychlování.
- Jaká bude jeho rychlost po uplynutí 0,2 s, pokud bude volně puštěn dolů?
- Jaká bude jeho rychlost po uplynutí 0,2 s, pokud bude vržen dolů rychlostí 5 m/s?
- Jaká bude jeho rychlost po uplynutí 0,2 s, pokud bude vržen vzhůru rychlostí 5 m/s?
Z definice zrychlení a = Δv/Δt vyplývá, že Δv = a ⋅ Δt. Změnu rychlosti tedy určíme ze zrychlení a času. Konkrétně tedy pro míček Δv = a ⋅ Δt = 2 m/s.
- Volně puštěný míček má počáteční rychlost nulovou, proto výsledná rychlost bude v = 2 m/s.
- Počáteční rychlost míčku směřuje dolů, stejně jako zrychlení. Proto výsledná rychlost bude v = 5 m/s + 2 m/s = 7 m/s
- Počáteční rychlost míčku směřuje vzhůru, tedy opačně než zrychlení. Proto výsledná rychlost bude v = −5 m/s + 2 m/s = −3 m/s. Záporné znaménko nám říká, že směr rychlosti bude vzhůru, neboť osu x jsme zvolili směrem dolů (sami se můžete přesvědčit dosazením většího času za Δt, že míček se po nějaké době začne pohybovat směrem dolů a rychlost změní znaménko na kladné).
U automobilů je zvykem udávat dobu t, za kterou zrychlí z 0 na 100 km/h. Určete průměrné zrychlení aut v základních jednotkách pro tyto případy:
- Škoda Octavia 1,5 TSI: t = 8,7 s.
- Tesla model S: t = 2,6 s.
Stačí dosadit do definice zrychlení a = Δv/Δt. Musíme ale použít správné jednotky: Δv = 100 km/h ≈ 28 m/s. Proto:
- a = 3,2 m/s2.
- a = 10,7 m/s2.
Nejdřív určíme Δv = 72 km/h − 90 km/h = −18 km/h = −5 m/s. Záporné znaménko je v pořádku, říká nám, že vlak zpomaluje. Potřebné zrychlení je a = Δv/Δt = −0,5 m/s2.
Je přirozené si zvolit orientaci osy x ve směru pohybu. Potom okamžitá rychlost vx je kladná a zrychlení ax je kladné, když těleso zrychluje, a záporné, když zpomaluje. Záporné zrychlení tedy znamená zpomalování. Pokud ovšem těleso začne couvat čili pohybovat se proti směru osy x, je vx záporné, a pokud se navíc tato rychlost v záporném směru zvětšuje, musí být při takovém zrychlování ax záporné. Přehledně to ilustruje následující pohyb výtahu.
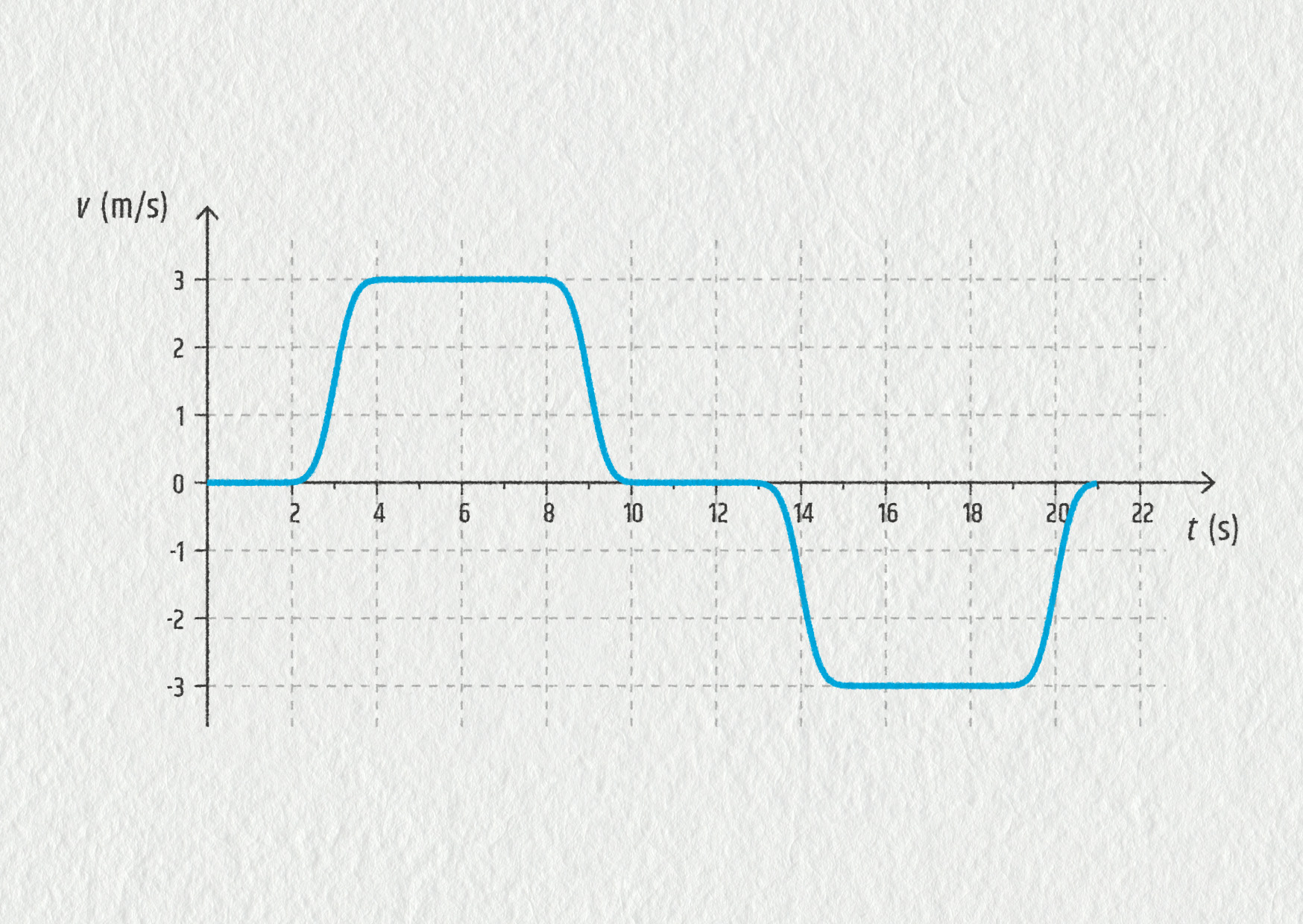
Zdroj
Jak z grafu pro rychlost určíme změnu polohy?
Graf v(t) má ještě jednu užitečnou vlastnost. Můžeme pomocí něj počítat změnu polohy tělesa nebo také uraženou dráhu.
Celková změna polohy Δx je rovna obsahu plochy pod křivkou v grafu v(t).
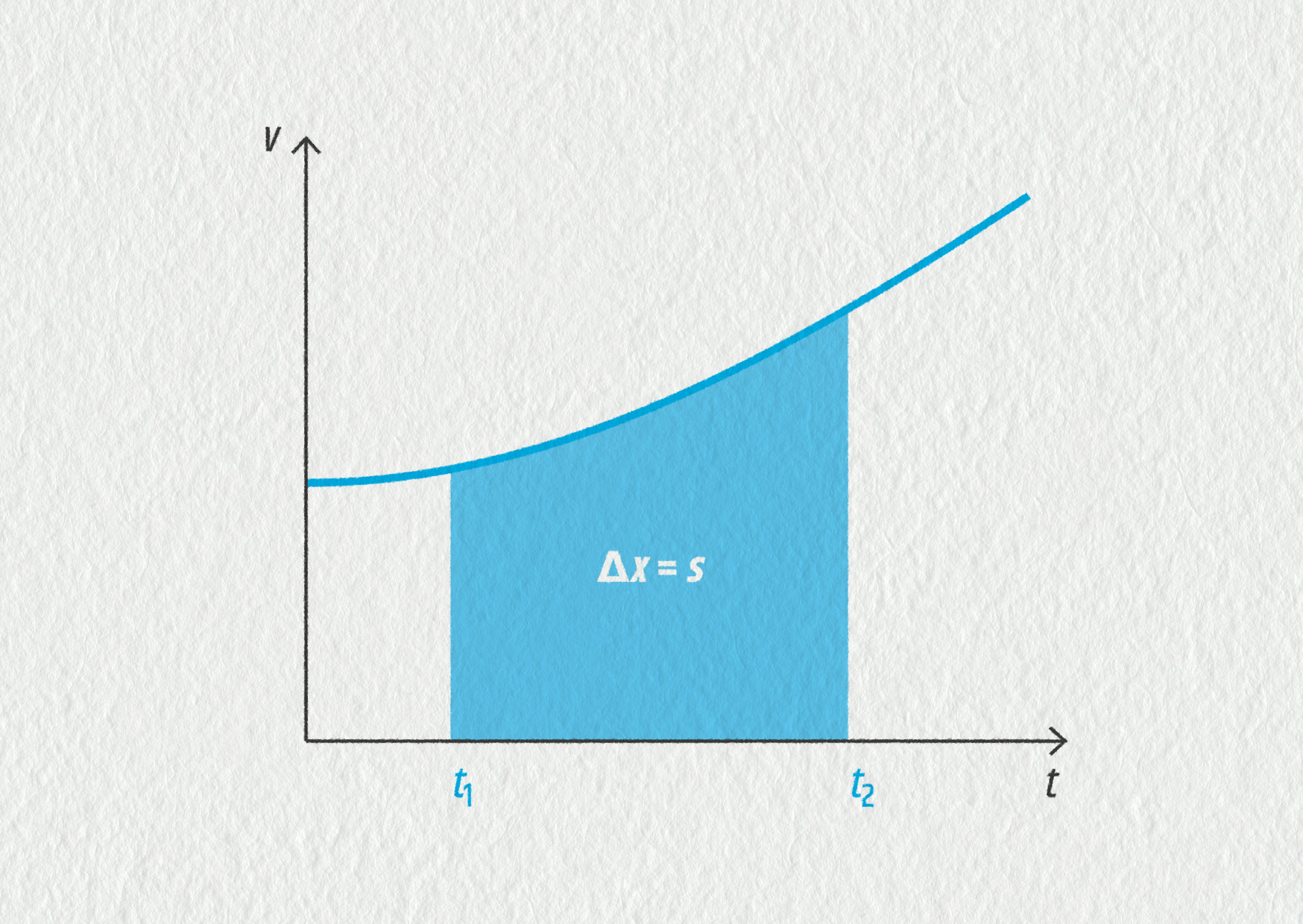
Zdroj
K odvození nám pomůže další obrázek:
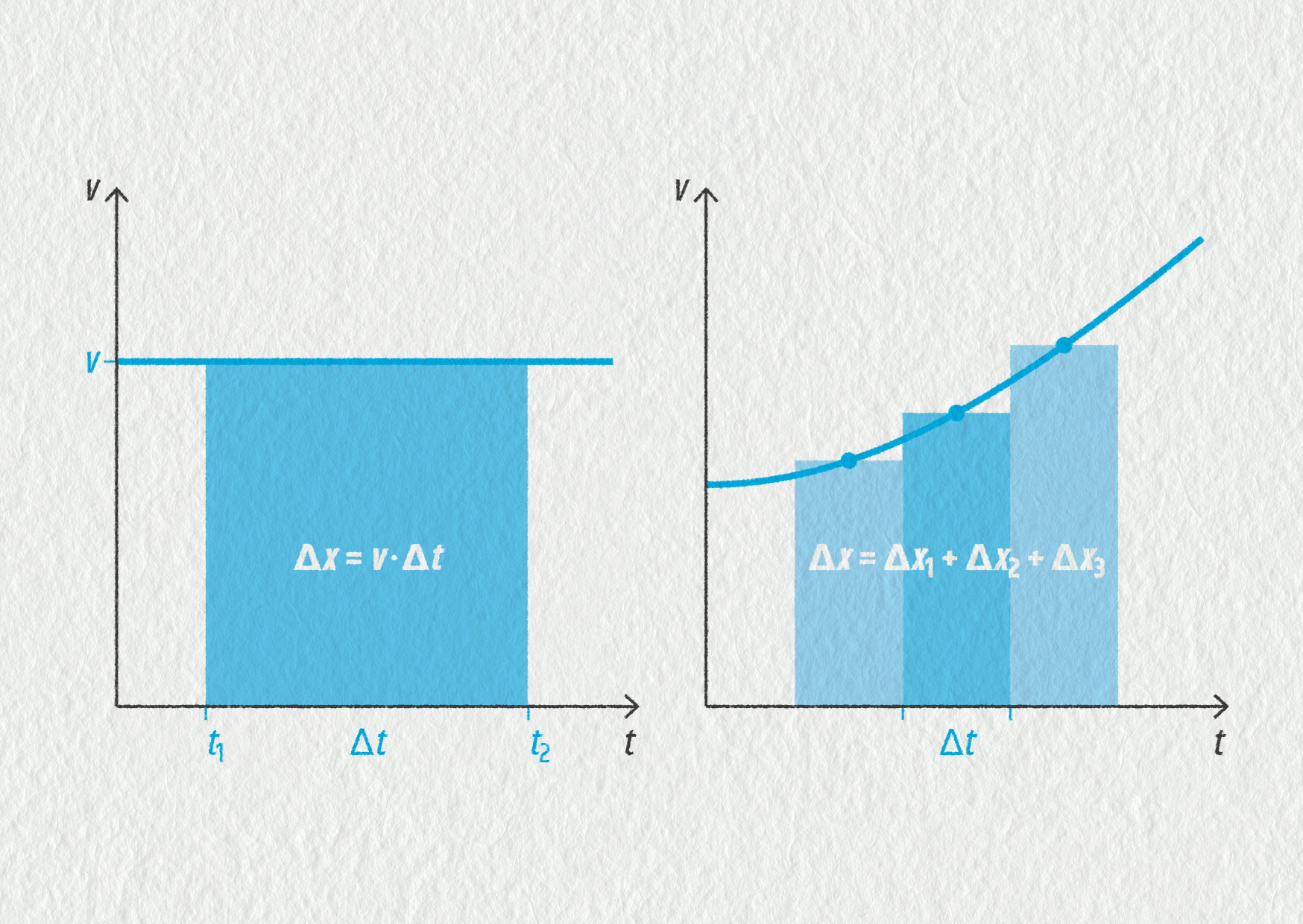
Zdroj
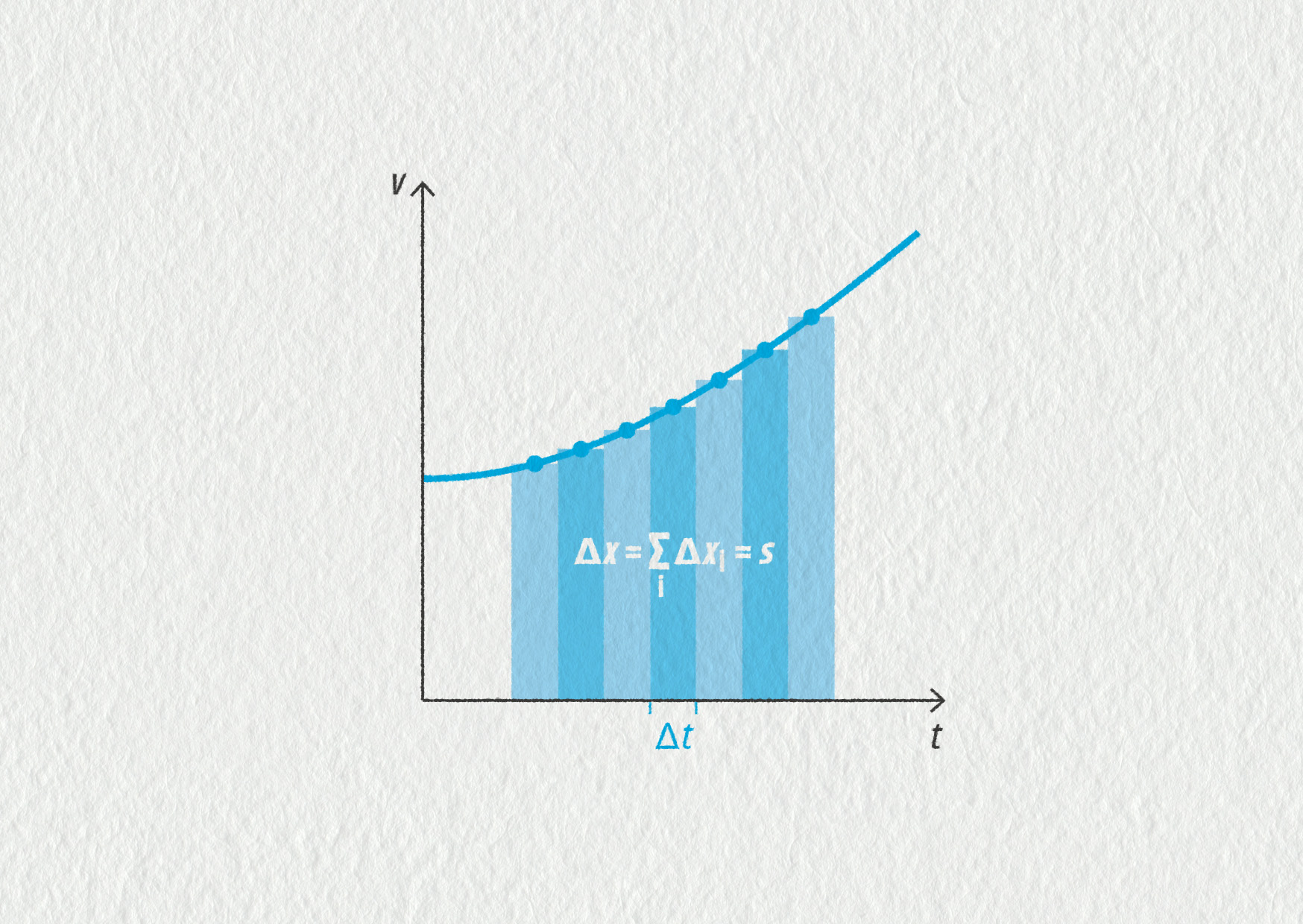
Zdroj
Prakticky si vše vyzkoušíme ve dvou úlohách:
Majitel elektromobilu si dal záležet, aby jeho rozjezd probíhal plynule. Díky tomu můžete z grafu jeho rychlosti snadno určit, jakou vzdálenost ujel během prvních tří sekund od startu.

Zdroj
Uraženou dráhu určíme jako obsah plochy pod křivkou. V tomto případě jde o obsah pravoúhlého trojúhelníku: s = S = 1/2 ⋅ 20 m/s ⋅ 3 s = 30 m.
Hráč baseballu vyhodil míč svisle vzhůru a poté jej zase chytil. Graf ukazuje okamžitou rychlost míče v závislosti na čase (osa x směřovala vzhůru). Z grafu určete:
- jak vysoko míč vyletěl,
- jakou urazil celkovou dráhu.
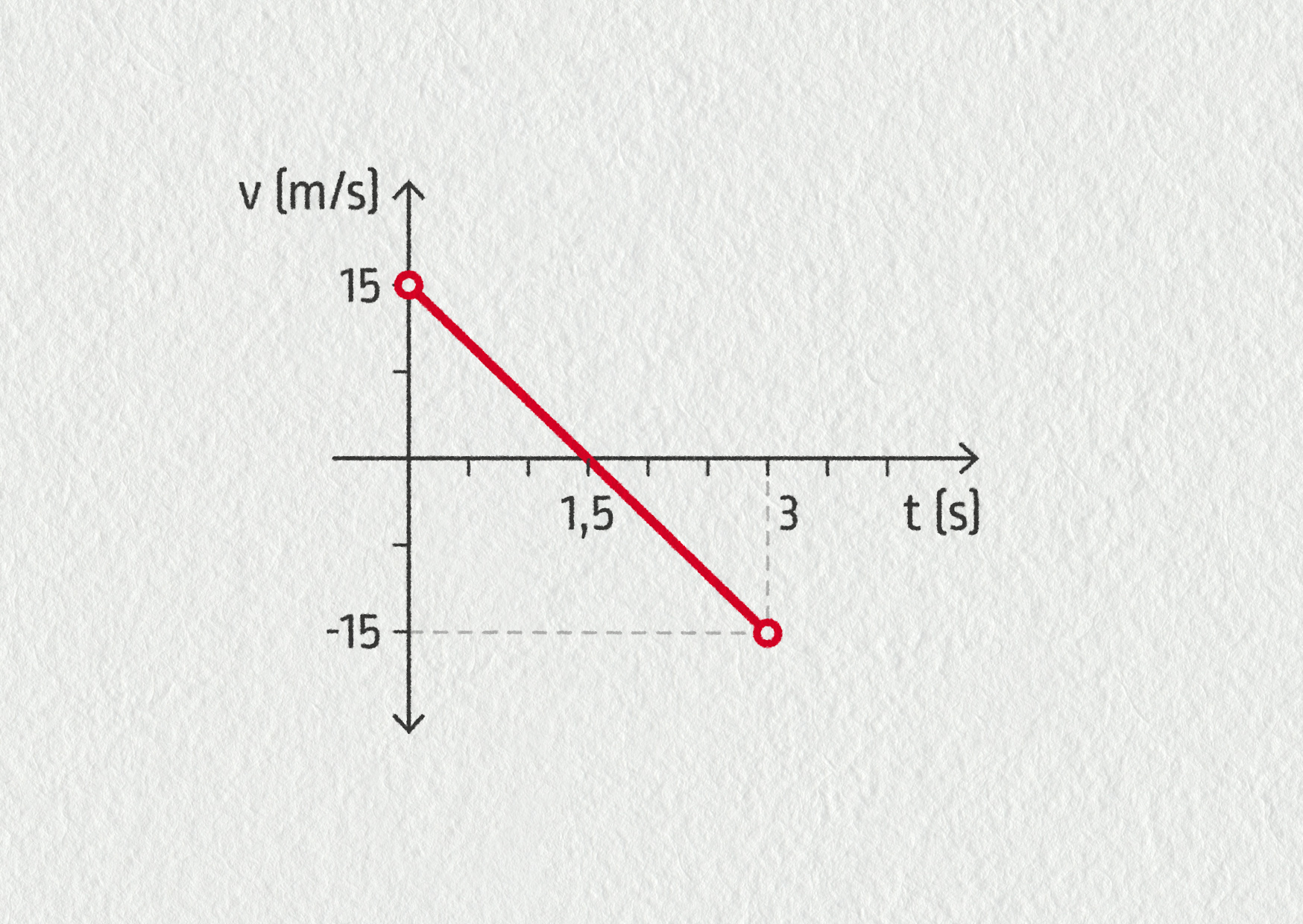
Zdroj
V této úloze se objevuje záporná rychlost. Už víme, že to znamená pohyb proti směru zvolené osy x. Vidíme, že míč 1,5 s letěl vzhůru a zpomaloval, pak se otočil a 1,5 s letěl zase dolů a zrychloval. Výšku výstupu míče proto spočítáme jako obsah pravoúhlého trojúhelníku: s = S = 1/2 ⋅ 15 m/s ⋅ 1,5 s = 11,25 m. Celková uražená dráha je logicky dvojnásobná, tedy 22,5 m.
Poznámka: Let směrem dolů je v grafu reprezentován shodným trojúhelníkem jako let vzhůru, pouze pod osou x. Pokud bychom jeho obsah započítali se záporným znaménkem, vyjde nám celková změna polohy Δx = 0, a to je správně – míč se vrátil zpět na původní místo. Pokud jeho plochu započítáme s kladným znaménkem, vyjde nám uražená dráha.
Jak měříme rychlost a zrychlení?
Polohu umíme měřit pomocí sonaru či radaru. Jak můžeme měřit rychlost? Použijeme definici okamžité rychlosti v = Δx/Δt a rychlost vypočítáme ze změny polohy Δx (takto funguje například tachometr nebo GPS). Rychlost je možné měřit také například pomocí Dopplerova jevu (policejní radar).
Také zrychlení můžeme vypočítat pomocí změny rychlosti Δv. Můžeme ho měřit pomocí akcelerometru. Ten funguje na základě měření síly a jeho princip je na obrázku. Při zrychleném pohybu dochází k deformaci nosníku (viz obrázek). Deformace nastává taky působením gravitace. Díky tomu můžeme měřit jak zrychlení, tak gravitační pole (akcelerometr je od sebe nedokáže odlišit). Z toho vyplývá i často používaná jednotka zrychlení g = 9,8 m/s2. Pro měření zrychlení v libovolném směru je potřeba trojosý akcelerometr (viz obrázek). Ten je součástí každého chytrého telefonu jako součástka o rozměrech několika milimetrů. Díky tomu telefon pozná svoji orientaci v gravitačním poli, ale můžete s ním pomocí vhodné aplikace také měřit zrychlení při pohybu.

Zdroj
Jako akcelerometr funguje i lidské tělo. Nedokáže vnímat rychlost, kterou se pohybuje, ale dokáže vnímat velikost a směr zrychlení. Jednak pomocí rovnovážného ústrojí, které se nachází v uchu, a jednak pomocí deformace celého těla. Velké zrychlení si užíváme například při jízdě na horské dráze. Pokud je ale zrychlení příliš velké, nastávají problémy. Například při dopravní nehodě dojde k prudkému zpomalení auta, které nám může způsobit vážná zranění. Některé hodnoty zrychlení (v jednotkách g) uvádíme v tabulce.
| rozjezd závodního auta | až 2 g |
| horská dráha | až 4 g |
| limit pro leteckou akrobacii | 12 g |
| dopravní nehoda | až 100 g |

