Abychom mohli zkoumat pohyb, musíme umět jednoduše určovat a měřit polohu. Tělesa mohou mít složitý tvar, mohou být pružná a ohebná, třeba jako lidské tělo. Popsat přesně polohu takového tělesa je dost složité. Museli bychom ho modelovat pomocí mnoha bodů. Tak se to dělá při počítačové animaci postavy na základě snímání živého herce – tzv. motion capture (viz obrázek).

Zdroj
Začněme něčím jednodušším: často nás zajímá jen pohyb tělesa jako celku. Pak si můžeme dovolit těleso nahradit jen jedním bodem. To je například při sledování trasy pomocí mobilu (viz obrázek) nebo při pohybu planet kolem Slunce. Pro fyziku je důležitá ještě hmotnost, proto se tento jednoduchý model označuje jako hmotný bod. Ať je těleso sebevětší, jeho rozměry a tvar nás při tomto zjednodušení nezajímají.
Zdroj
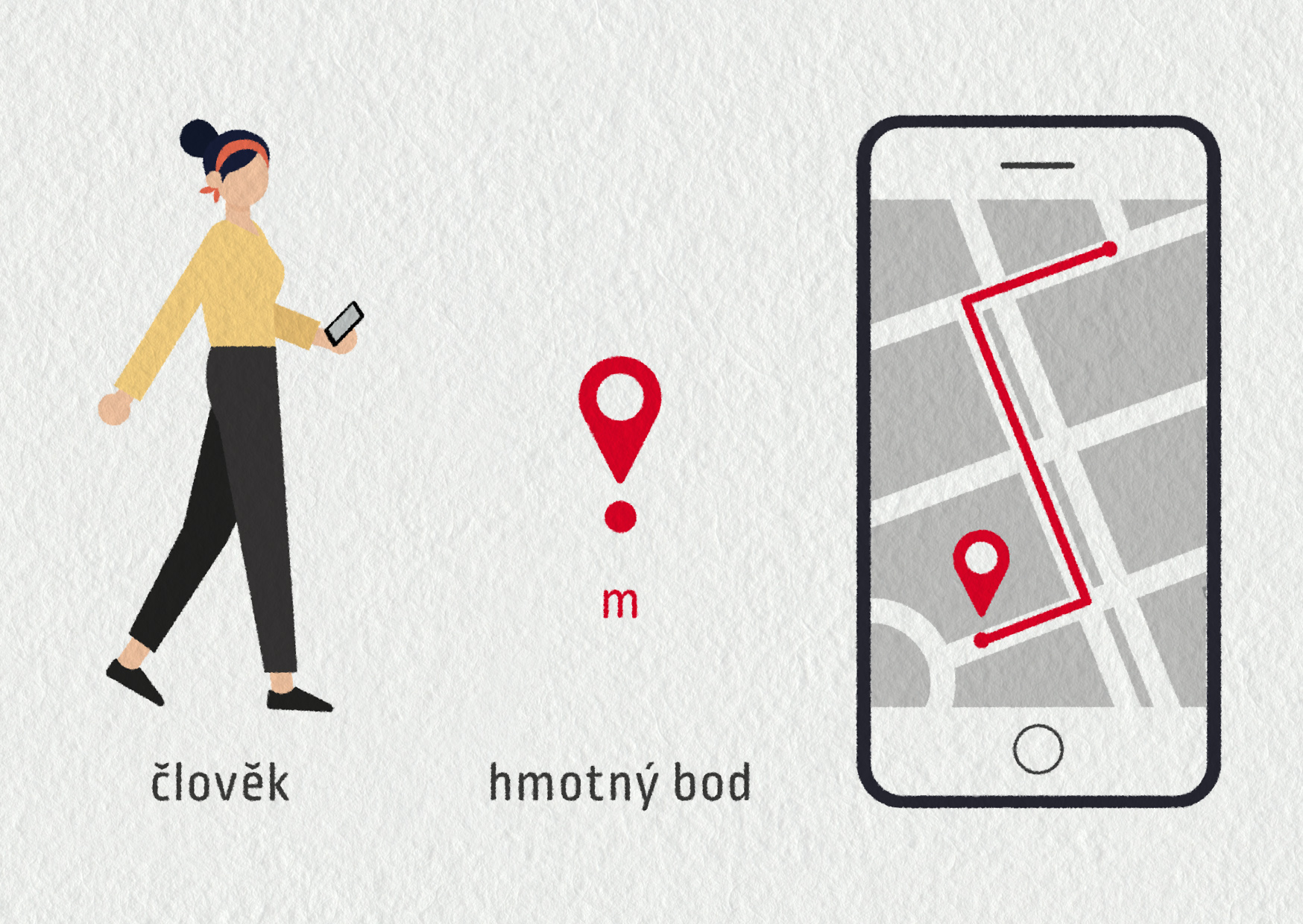
Pro popis polohy bodu používáme vynález matematika a filozofa Reného Descarta – kartézské souřadnice. Jde o jednu, dvě nebo tři na sebe kolmé osy. Systém souřadnicových os ještě musíme umístit do konkrétního bodu a určit orientaci všech os. Tím definujeme vztažnou soustavu. Názorně to ukazují následující příklady:
Jednorozměrný pohyb
Jednorozměrný pohyb je takový, který je omezen na přímku nebo křivku. Představte si, že máte za úkol vymyslet systém sledování polohy výtahu. To je nutné pro jeho přesné ovládání. Jak to uděláte? Výtah se pohybuje pouze v jednom směru – po přímce. Proto nám bude stačit jen jedna souřadnice, volba nulové polohy a kladného směru osy x. Těleso kabiny nahradíme vhodně zvoleným bodem, jehož polohu budeme popisovat (viz obrázek). Pokud zadáte např. x = 6,25 m, je tím poloha výtahu zcela jednoznačně určena ve vámi zvolené vztažné soustavě. Pro lepší představu navštivte naši animaci.
Dvourozměrný pohyb
Dvourozměrný neboli dvoudimenzionální (2D) pohyb je omezen na rovinu nebo plochu. Potřebujeme-li například popsat polohu robota pohybujícího se po podlaze výrobní haly, jedná se o pohyb v rovině tvořené podlahou. K popisu polohy jsou zde potřeba dvě osy a samozřejmě také počátek soustavy souřadnic.
Trojrozměrný pohyb
Přidáním třetí souřadnice pak můžeme obdobně popsat polohu v trojrozměrném prostoru (3D). Jako praktický příklad jsme zvolili polohu letadla v prostoru (viz obrázek).
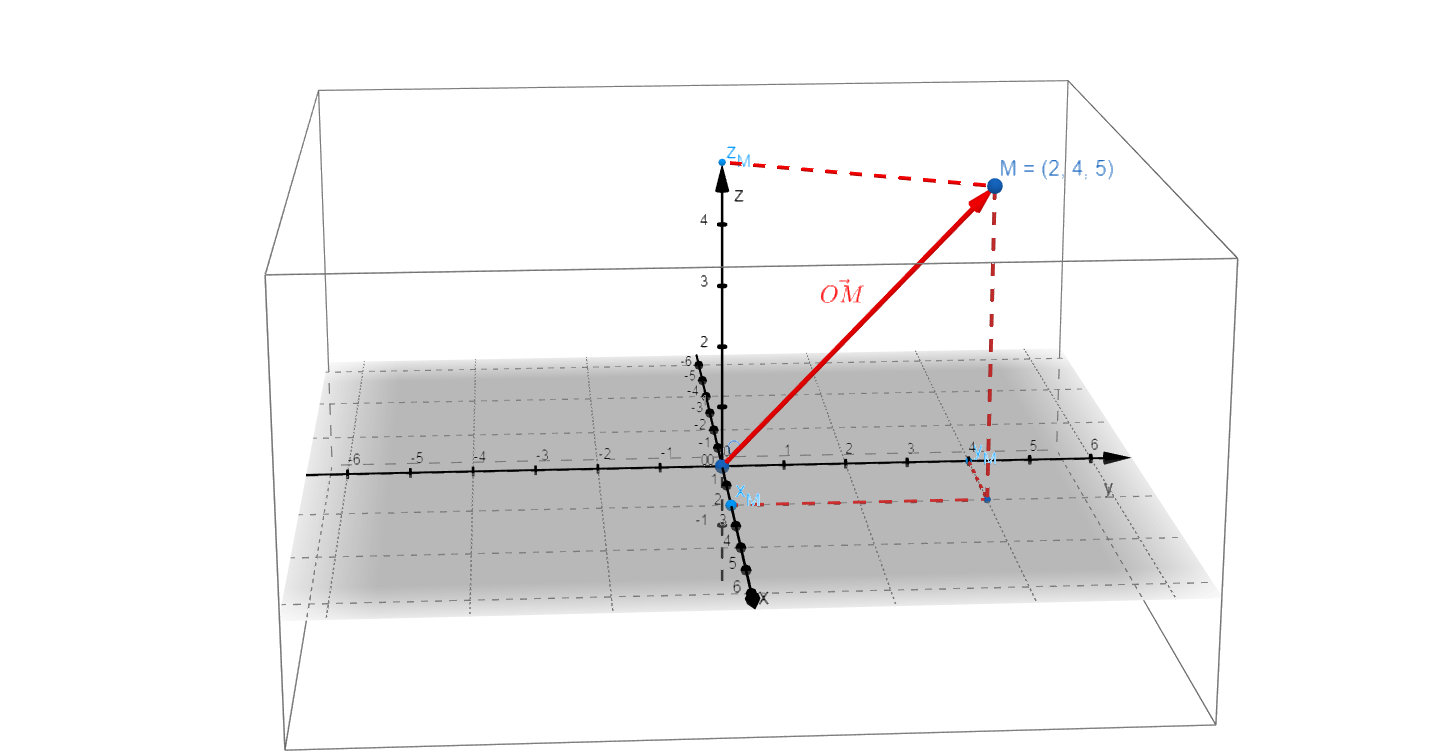
Zdroj
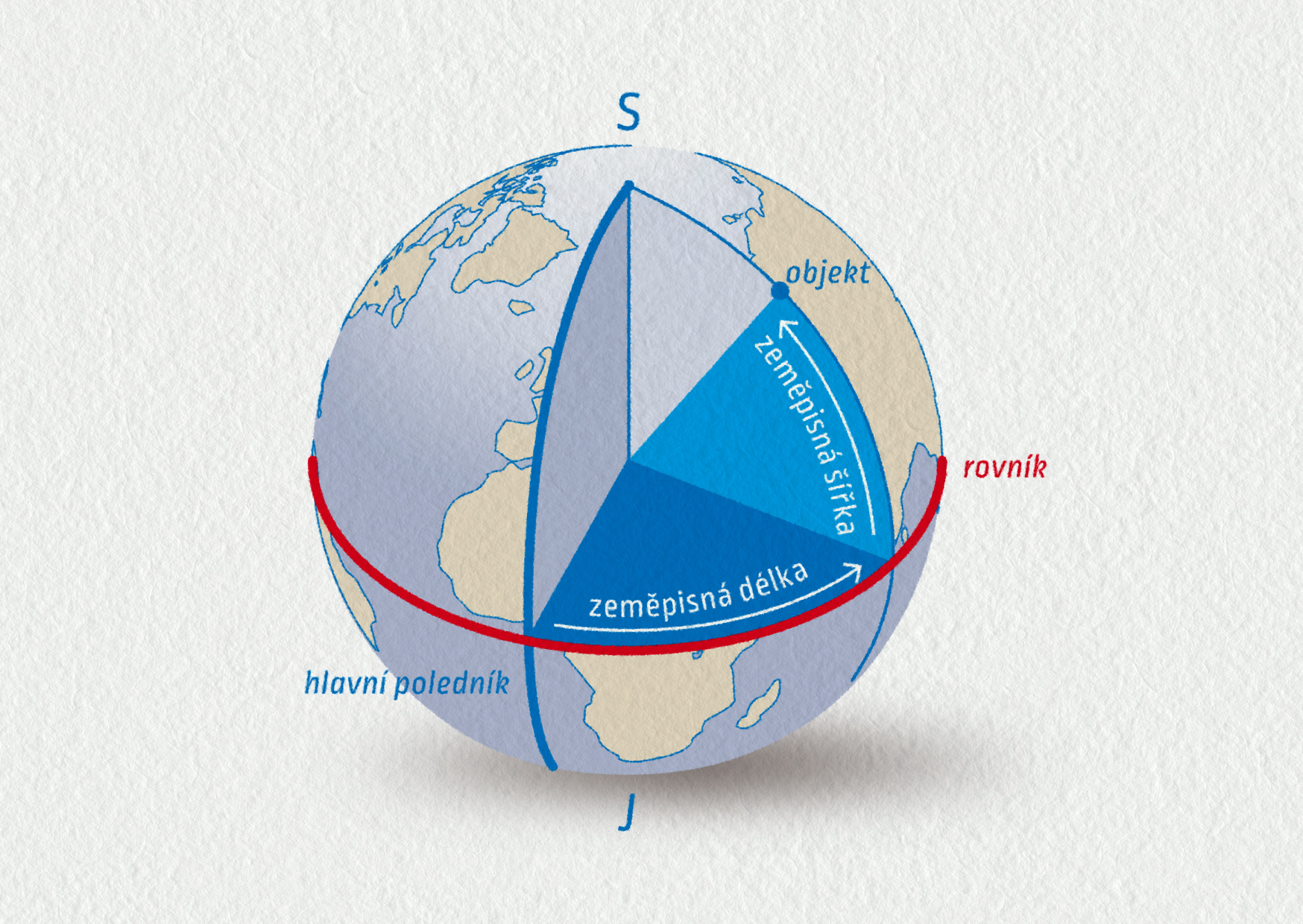
Pro určování polohy na Zemi se místo kartézských souřadnic používají souřadnice sférické. Podstatné je, že souřadnice musí být zase tři, abychom popsali polohu ve třech dimenzích. Jsou to zeměpisná šířka (úhel od –90 do 90 stupňů), zeměpisná délka (úhel od –180 do 180 stupňů) a nadmořská výška (vzdálenost). S tou je trochu problém, protože přesnější by bylo ji nahradit vzdáleností od počátku soustavy souřadnic (středu Země). V čem spočívá výhoda sférických souřadnic v tomto případě? Je možné je změřit (viz měření polohy na Zemi), protože Země má přibližně tvar koule. Navíc nám často při pohybu po zemském povrchu, tedy při dvourozměrném pohybu, stačí dvě souřadnice. To by v kartézských souřadnicích nebylo možné.
Zdroj
Jak můžeme zaznamenat pohyb?
Náš svět je trojrozměrný, proto často pracujeme ve třech dimenzích. My se v této kapitole zatím omezíme jen na studium jednorozměrného pohybu, který je matematicky jednodušší. K pohybu v rovině a v prostoru se vrátíme v kapitolách 14 a 15.
Z předchozí kapitoly už víme, že vzdálenost objektů je možné měřit pomocí sonaru nebo radaru. Budeme tedy sledovat pohyb autíčka na stole pomocí sonaru (viz obrázek).

Zdroj
Zdroj
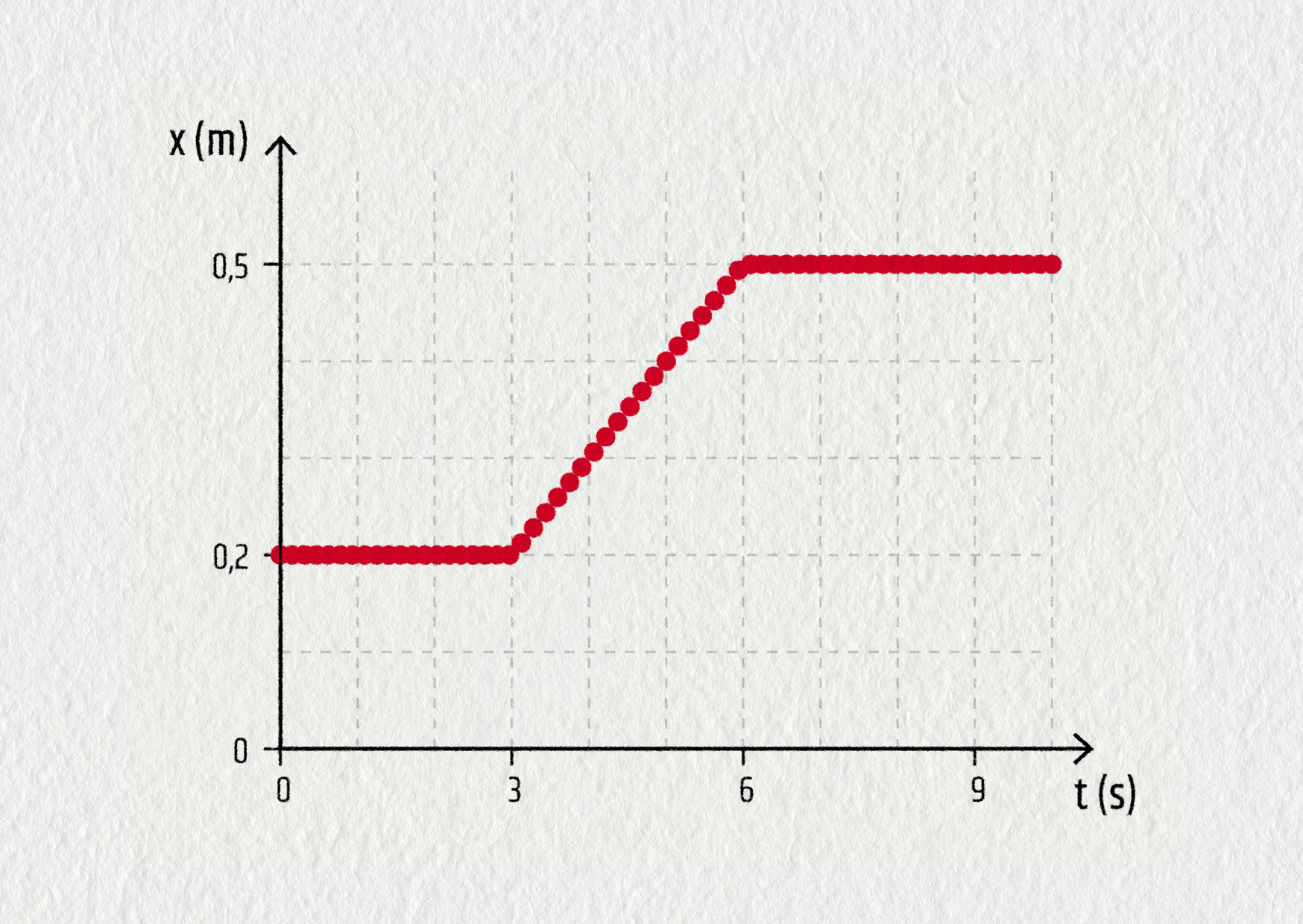
Pojďme se podívat na záznam pohybu autíčka. V grafu vidíme, jak se měnila jeho poloha v čase. Každé měření polohy je zobrazeno jako jeden bod v grafu. Vzorkovací frekvence byla 7 Hz, to znamená, že jsme polohu měřili 7krát za sekundu. Osa x má počátek v místě sonaru a je orientovaná směrem k autíčku. Získali jsme graf funkce x(t) – závislost polohy x na čase t.
Popište slovy, jak se podle grafu na obrázku autíčko pohybovalo, a určete z grafu o jeho pohybu co nejvíc informací.
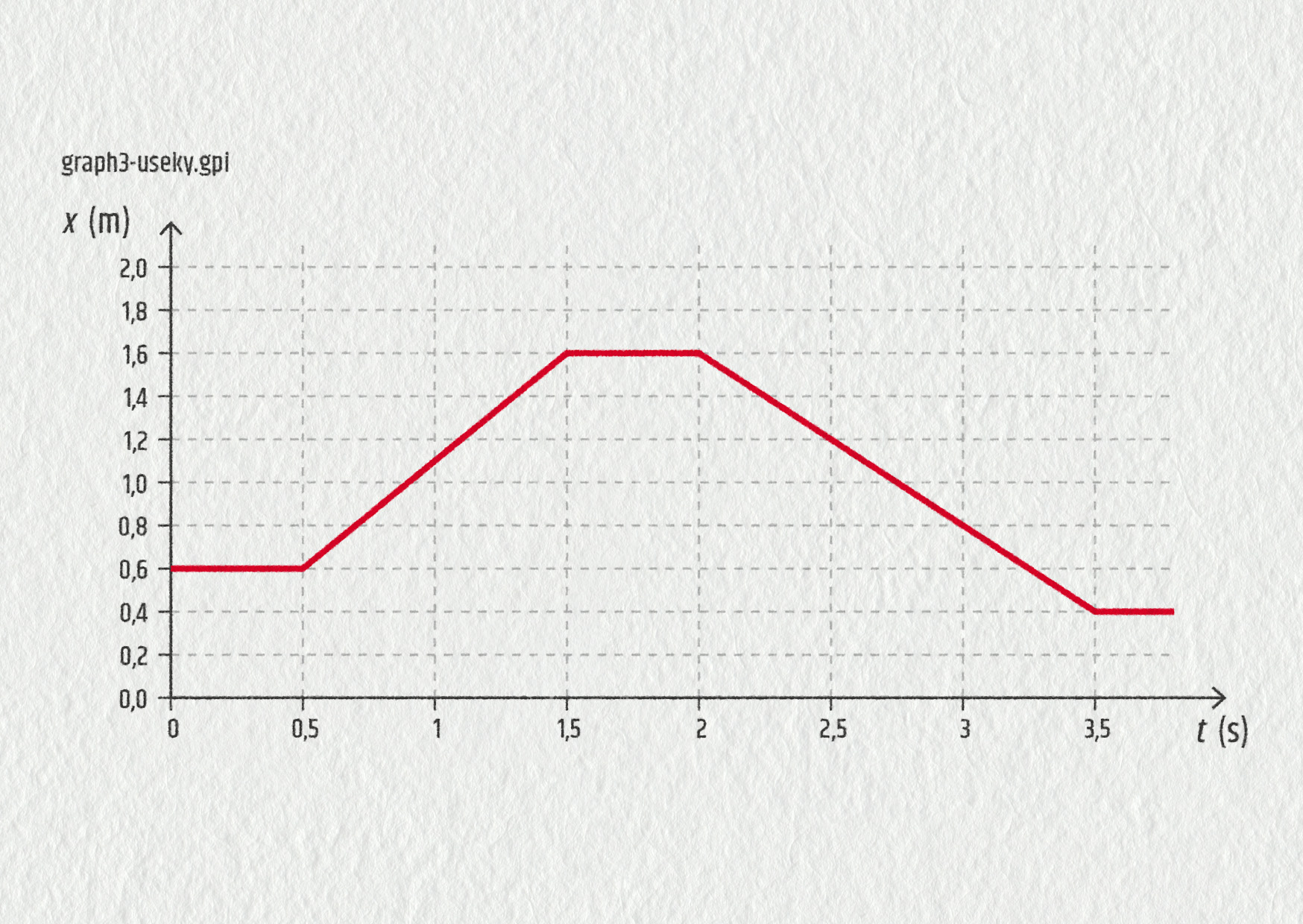
Zdroj
Funkce jsou velmi dobrým nástrojem k popisu pohybu, proto si připomeňme jejich důležité vlastnosti.
Funkce jednoznačně přiřazuje hodnotám proměnné x hodnoty proměnné y. Můžeme ji zadat tabulkou, grafem či předpisem:
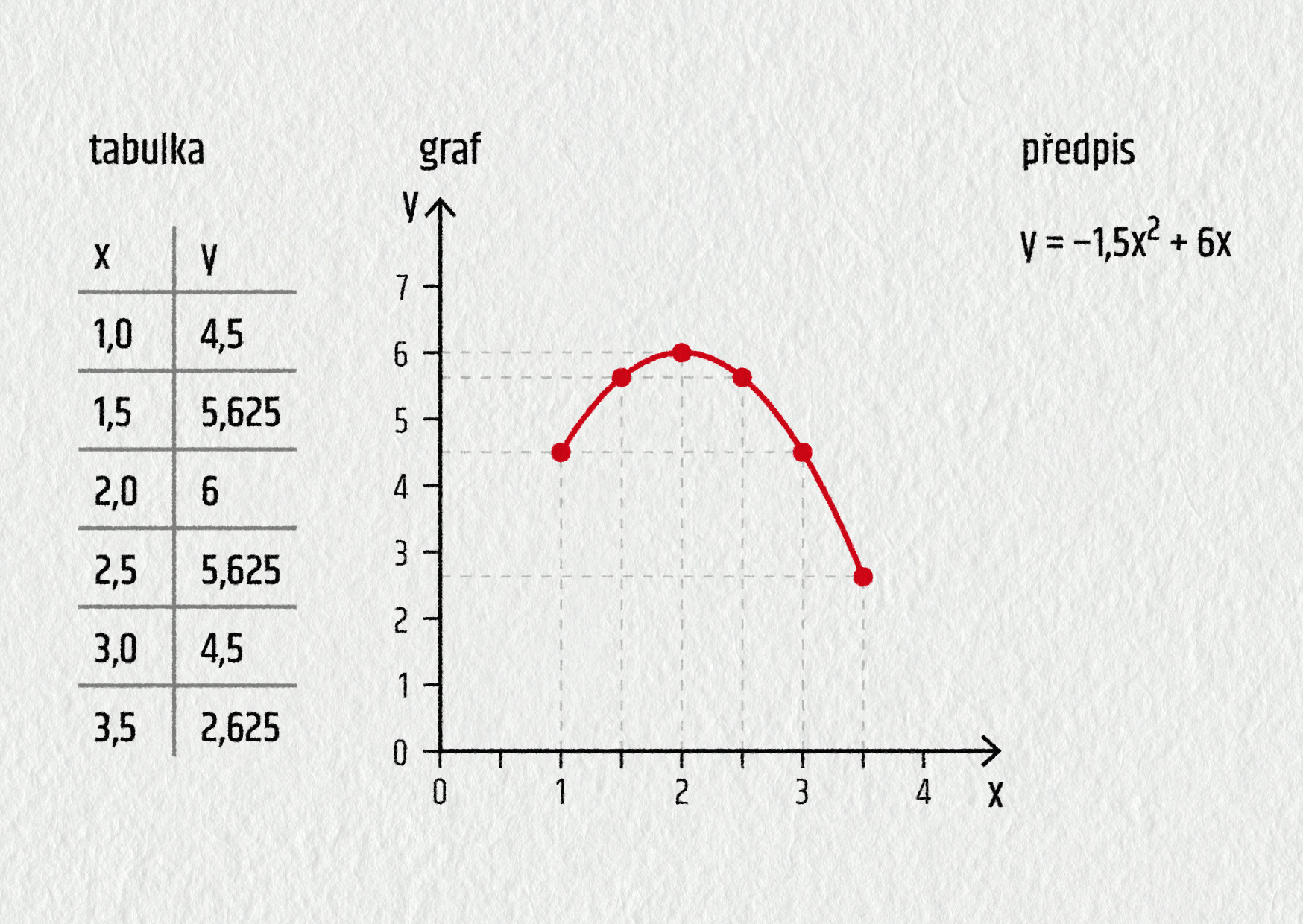
Zdroj
- x(t) závislost polohy (na ose x) na čase,
- y(t) závislost polohy (na ose y) na čase,
- v(t) závislost rychlosti na čase.
Měřením vždy získáme pouze soubor bodů ve formě dvojic x, y, popřípadě x, t a podobně. Ty můžeme zaznamenat do tabulky nebo grafu, kde se objeví jako jednotlivé body. Předpis funkce nebo graf ve formě spojité křivky je možné doplnit teprve po zpracování změřených dat. Tomu se budeme věnovat v závěru kapitoly.