Odpor vzduchu
Úkol: Zjistěte, jak závisí odporová síla na rychlosti. Na základě experimentu rozhodněte, zda je velikost odporové síly vzduchu přímo úměrná rychlosti, nebo její druhé mocnině.
Vybavení: sada kávových filtrů, sonar, počítač, stojan.

Zdroj
Když ve fyzice řešíme situace týkající se volného pádu, často zanedbáváme odporovou sílu a předpokládáme tak, že je zrychlení padajícího tělesa konstantní. Ve skutečnosti však všechna tělesa s konstantním zrychlením nepadají. Naopak, jejich pohyb se vlivem odporové síly stane rovnoměrným a zrychlení bude mít nulovou hodnotu.
Při pádu tělesa o hmotnosti m na něj totiž působí dvě síly: tíhová \(\Vec{F}_\mathrm{G}\) o velikosti \(mg\) a opačně orientovaná odporová síla \(\Vec{F}_\mathrm{O}\) , jejíž velikost můžeme vyjádřit buď jako \(kv\) nebo jako \(cv^2\). Když se vlivem zrychlování tělesa tyto síly vyrovnají, těleso dosáhne maximální rychlosti vmax a dále již nezrychluje. Pohyb je rovnoměrný.
Píšeme \(mg=kv_\mathrm{max}\) nebo \(mg=cv^2_\mathrm{max}\). Vidíme tedy, že hmotnost tělesa je buď úměrná maximální rychlosti vmax, nebo její druhé mocnině.
\(v_\mathrm{max}\sim m\) nebo \(v^2_\mathrm{max}\sim m\)
O tom, který z těchto vztahů odpovídá skutečnosti, můžete rozhodnout v následujícím experimentu.
Postup měření:
- Sestavte aparaturu dle obrázku. Sonar upevněte do dostatečné výšky, stačí 2,5 m nad podlahu.
- V režimu měření si nastavte dobu měření na 3 s, frekvenci měření 40 Hz a trigger start měření od 0,25 m; nechte si zobrazit cca 40 bodů před startem měření.
- Umístěte ruku s kávovým filtrem 10 cm pod sonar, zapněte měření a nechte kávový filtr padat. Počítač zaznamená závislost polohy a rychlosti na čase.
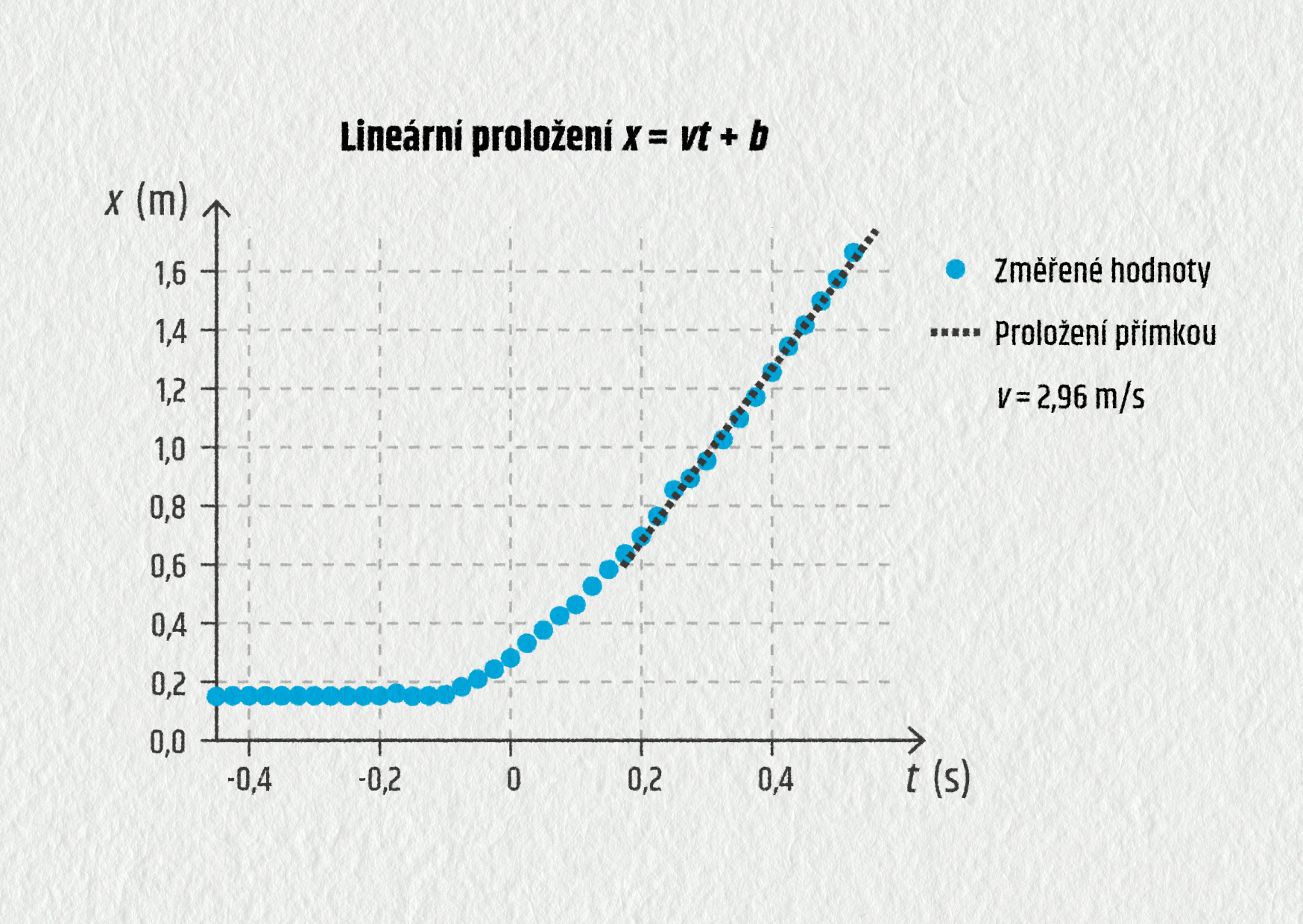
4.61 – Ukázka proložení naměřených dat.
Zdroj - Z grafu polohy odstraňte všechny případné chybové body (sonar nemusí vždy dobře zaznamenat polohu malého tělesa), popřípadě pokus opakujte.
- Proložte posledních cca 15 naměřených bodů přímkou a z její rovnice určete maximální rychlost filtru vmax.
- Pokus postupně opakujte pro 2–5 kávových filtrů vložených do sebe. Výsledky zapisujte do tabulky, doplňte všechny výpočty.
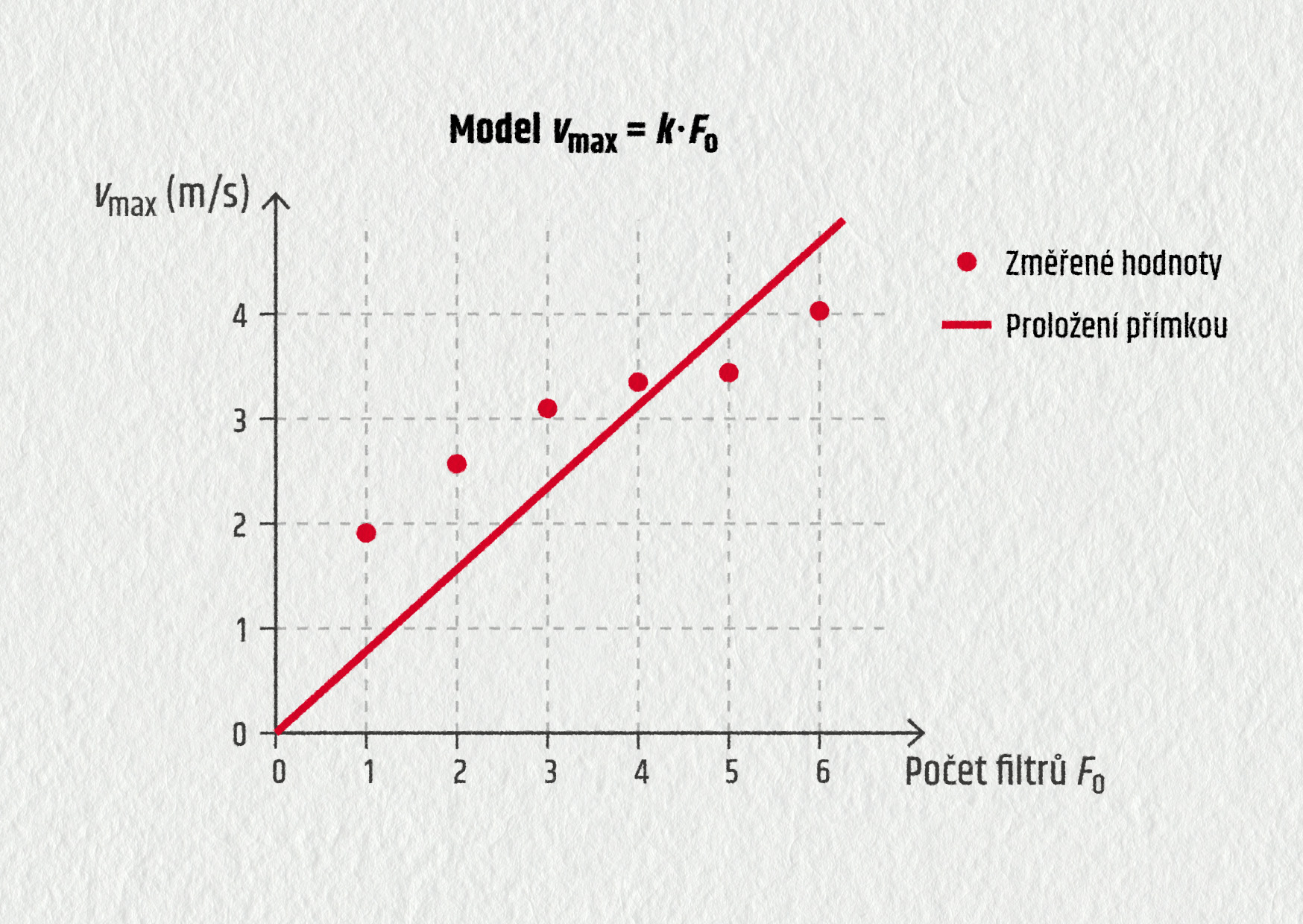
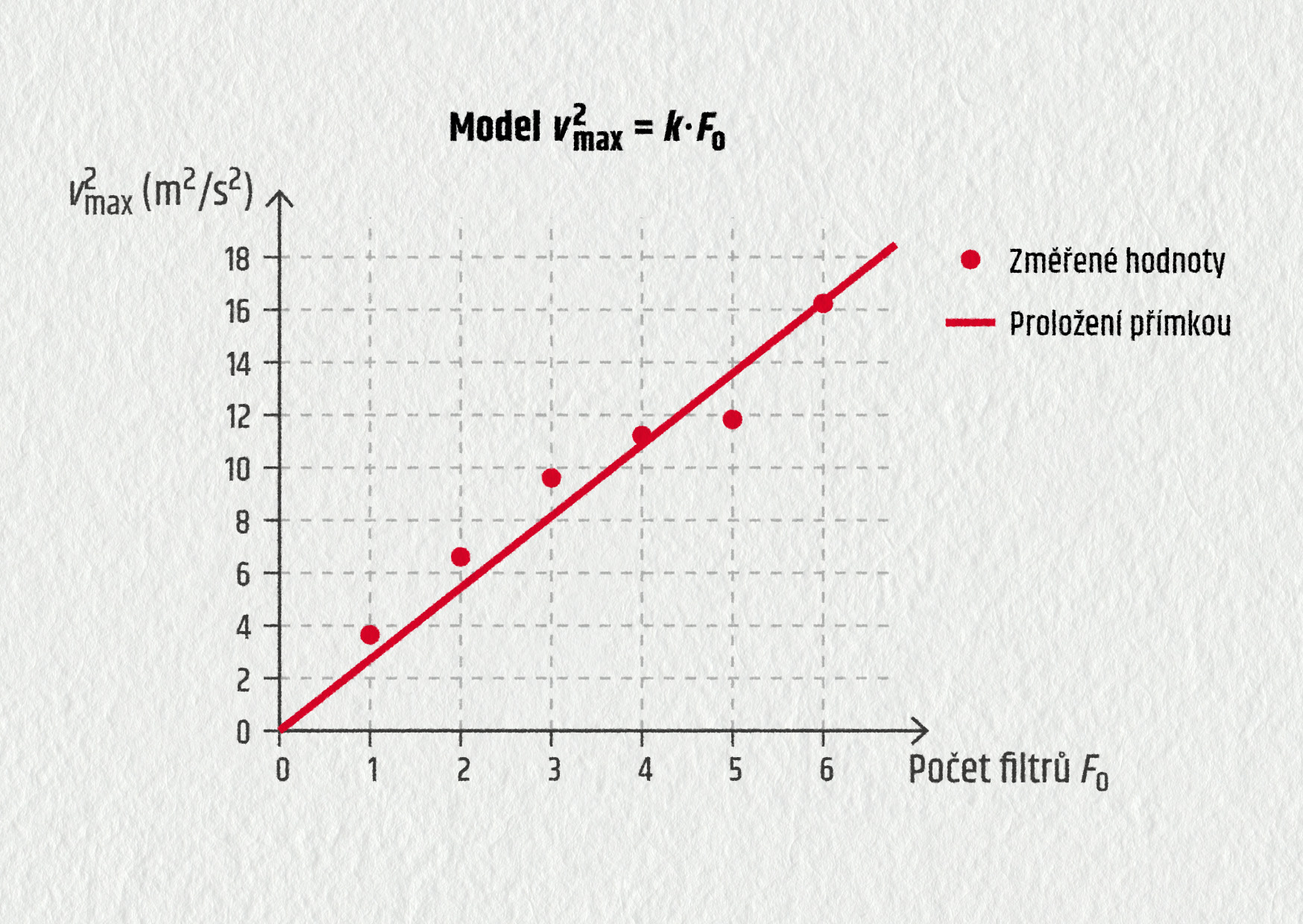
počet filtrů vmax (m/s) v2max (m2/s2) 1 2 3 4 5 - Sestrojte grafy závislostí \(v_\mathrm{max} = f(m)\) a \(v^2_\mathrm{max} = f(m)\). Proložte jimi grafy přímých úměrností a rozhodněte, který z modelů odporové síly vyhovuje studované situaci.
Otázky:
- Jak by vypadal nárůst vzdálenosti bez odporu vzduchu? Načrtněte tento graf. Porovnejte s reálnou situací.
- Jak by vypadal nárůst rychlosti bez odporu vzduchu? Načrtněte tento graf. Porovnejte s reálnou situací.
Při realizaci úlohy narazíte na několik technických problémů, které však nejsou nepřekonatelné:
• Kávový filtr příliš „zatáčí“, nepadá rovně – prolomte jeho špičku dovnitř (viz foto).

Zdroj
• Laboratorní stojan nestačí délkou – improvizujte na chodbě, postavte stojan se sonarem na skříň…
• Naměřená data jsou příliš „chybová“ – proveďte měření znovu, nebo odstraňte chybové hodnoty.

Zdroj
Ukázka výsledků:
| počet filtrů | vmax (m/s) | v2max (m2/s2) |
|---|---|---|
| 1 | 2,08 | 4,33 |
| 2 | 2,52 | 6,35 |
| 3 | 2,88 | 8,29 |
| 4 | 3,33 | 11,09 |
| 5 | 3,53 | 12,46 |
| 6 | 4,05 | 16,40 |
Zdroj
Zdroj

