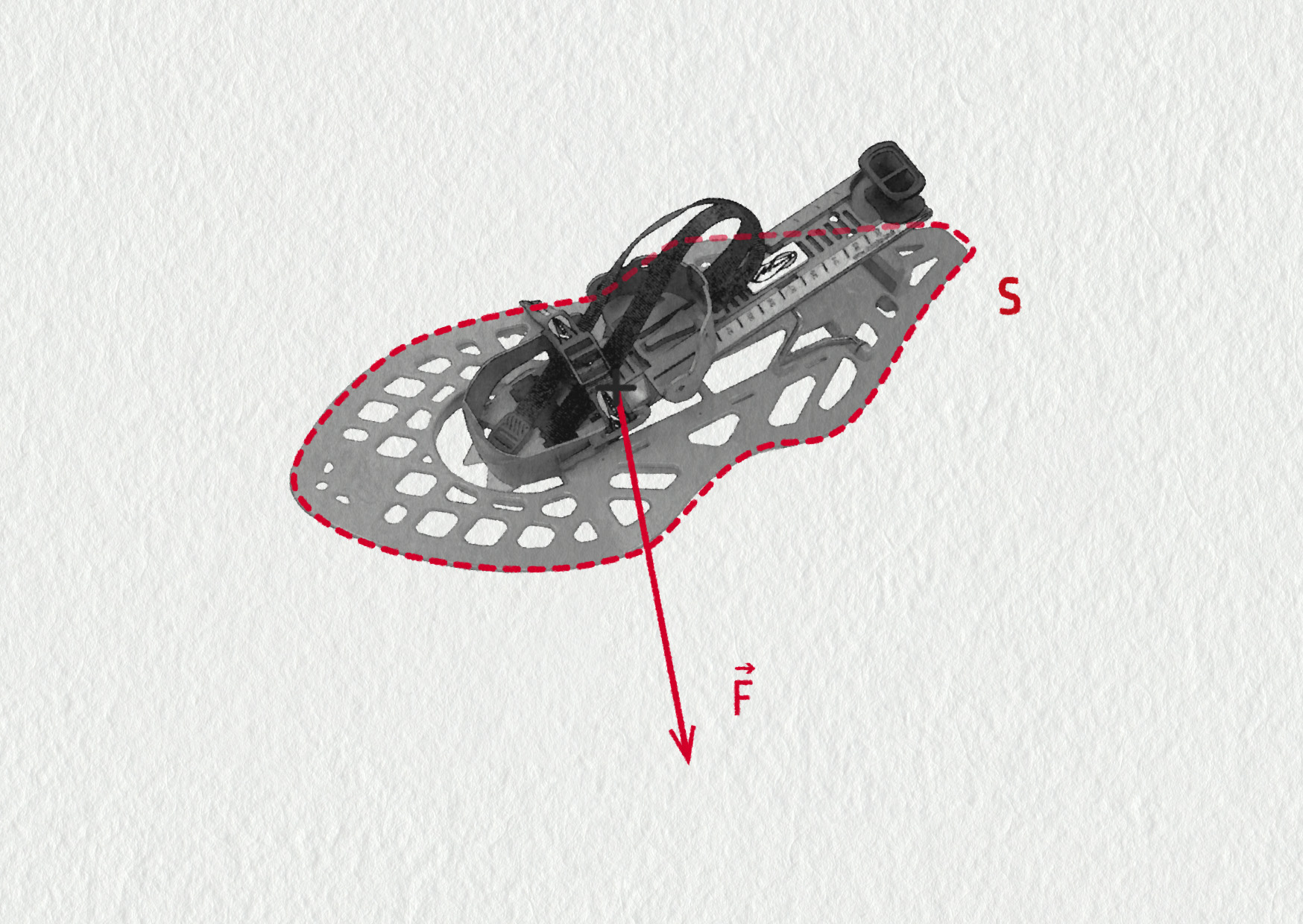
Tlak je velmi užitečná veličina. Můžeme se o tom přesvědčit například při chůzi v hlubokém sněhu. Aby se nohy do sněhu nebořily, je třeba zvětšit plochy, kterou se dotýkáme sněhové vrstvy. Můžeme použít lyže nebo sněžnice (viz obrázek). Tlaková síla, kterou působí noha na sníh, se přitom nezmění, ale síla se rozloží do větší plochy. Jinými slovy: zmenší se tlak mezi botou a sněhem a sníh se díky tomu neproboří.

Zdroj
Takto můžeme pomocí tlakové síly \(F\) a obsahu plochy \(S\), na kterou síla působí, definovat tlak
Definice tlaku: \(p=F/S\)
F ... velikost tlakové síly
S ... obsah plochy
Zdroj
Jednotkou tlaku je N/m2 = Pa (pascal). Tlak je skalární veličina: nemá směr (ve vzorci vystupuje velikost síly).
Blaise Pascal (1623–1662) byl francouzský fyzik, matematik a filosof. Pascal vynikal matematickým nadáním. Jako osmnáctiletý sestrojil pro svého otce pomůcku, počítací stroj, a stále ho vylepšoval. Proto po něm byl nazván programovací jazyk: Pascal. V matematice pak významně přispěl k rozvoji kombinatoriky, objevil uspořádání kombinačních čísel známé jako Pascalův trojúhelník. V určitém období svého života byl vášnivým hráčem a v té souvislosti položil – spolu se svým starším přítelem Pierrem Fermatem – základy teorie pravděpodobnosti.
Ve fyzice navázal na Torricelliho pokusy se rtuťovou trubicí. Provedl řadu přesných měření v různých nadmořských výškách. Tyto pokusy vyústily ve vynález výškoměru a posléze i barometru. Jako první přišel na myšlenku, že pomocí barometru je možno měřit výškový rozdíl dvou míst, a všiml si, že změna výšky rtuťového sloupce barometru může sloužit rovněž k předpovídání počasí. Výsledky shrnul v Pojednání o tlaku vzduchu z roku 1653. Dále objevil, že změny tlaku v kapalinách se šíří všemi směry stejně. Tento fakt se stal základem hydraulické techniky.
Po vážné nehodě v 33 letech se obrátil k mystice a filosofii a vstoupil do kláštera. Jeho filosofické poznámky vyšly až posmrtně jako Myšlenky o náboženství i jiných věcech.

Zdroj
Vypočítejte tlak pod sněžnicemi člověka o hmotnosti 60 kg. Obsah plochy jedné sněžnice je 0,1 m2, člověk stojí rovnoměrně na obou nohou.
\[ p=\frac{F}{S}=\frac{mg}{S} =\frac{60\cdot10}{2\cdot0{,}1}\ \mathrm{Pa} = 3\,000\ \mathrm{Pa} = 3\ \mathrm{kPa} \]
Tlak 1 Pa si můžete představit jako tlak vyvolaný volně ležícím kancelářským papírem o gramáži 100 g/m2. Často se proto setkáte s násobky kPa a MPa. Kromě toho se používá ještě jednotka bar neboli technická atmosféra. Její hodnota je přibližně odvozena od atmosférického tlaku: 1 bar = 100 kPa.
V této kapitole budeme zkoumat převážně plyny. Plyny a kapaliny označujeme jedním slovem jako tekutiny, neboť jejich společnou vlastností je právě tekutost. Tlak v tekutině je definován podobně jako tlak u pevných těles pomocí tlakové síly \(F\) a obsahu plochy \(S\). Podstatným rozdílem je fakt, že tlaková síla způsobí stejný nárůst tlaku ve všech místech tekutiny, zatímco v pevném tělese se takto jednoduše tlak nešíří (viz obrázky v galerii). Fakt, že změny tlaku se v kapalinách šíří všemi směry stejně, bývá na počest svého objevitele označován jako Pascalův zákon.
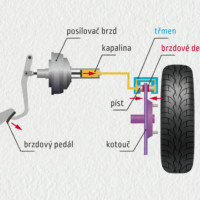
Z Pascalova zákona pak vyplývá, že tlak v tekutině nemá směr. O směru můžeme mluvit jen u tlakové síly. Pokud si vybereme libovolnou plochu (například stěnu nádoby, píst), bude na ni tekutina působit tlakovou silou \(F=pS\) vždy ve směru kolmém na zvolenou plochu. Snadné šíření tlaku v tekutinách se využívá v hydraulických zařízeních. Pomocí kapaliny můžeme přenášet a zvětšovat síly v hydraulickém lisu, automobilových brzdách nebo stavebních strojích.
Tlak a hydraulická zařízení

Zdroj

Zdroj
Zdroj

Zdroj
Dvě ruční pístové pumpy se liší pouze průměrem pístu. Jaký bude praktický rozdíl mezi oběma pumpami?
Tenčí píst dokáže při stejné síle vytvořit větší tlak, ale za to „zaplatíme“ menším objemem vzduchu při jednom stlačení.
Poznámka: gumové lodě se nafukují na poměrně nízký přetlak cca 0,2 bar. Naopak u závodních kol pro silniční cyklistiku se používají tzv. galusky, bezdušové pláště, které je třeba natlakovat na přibližně 10 bar.
Hydrostatický tlak
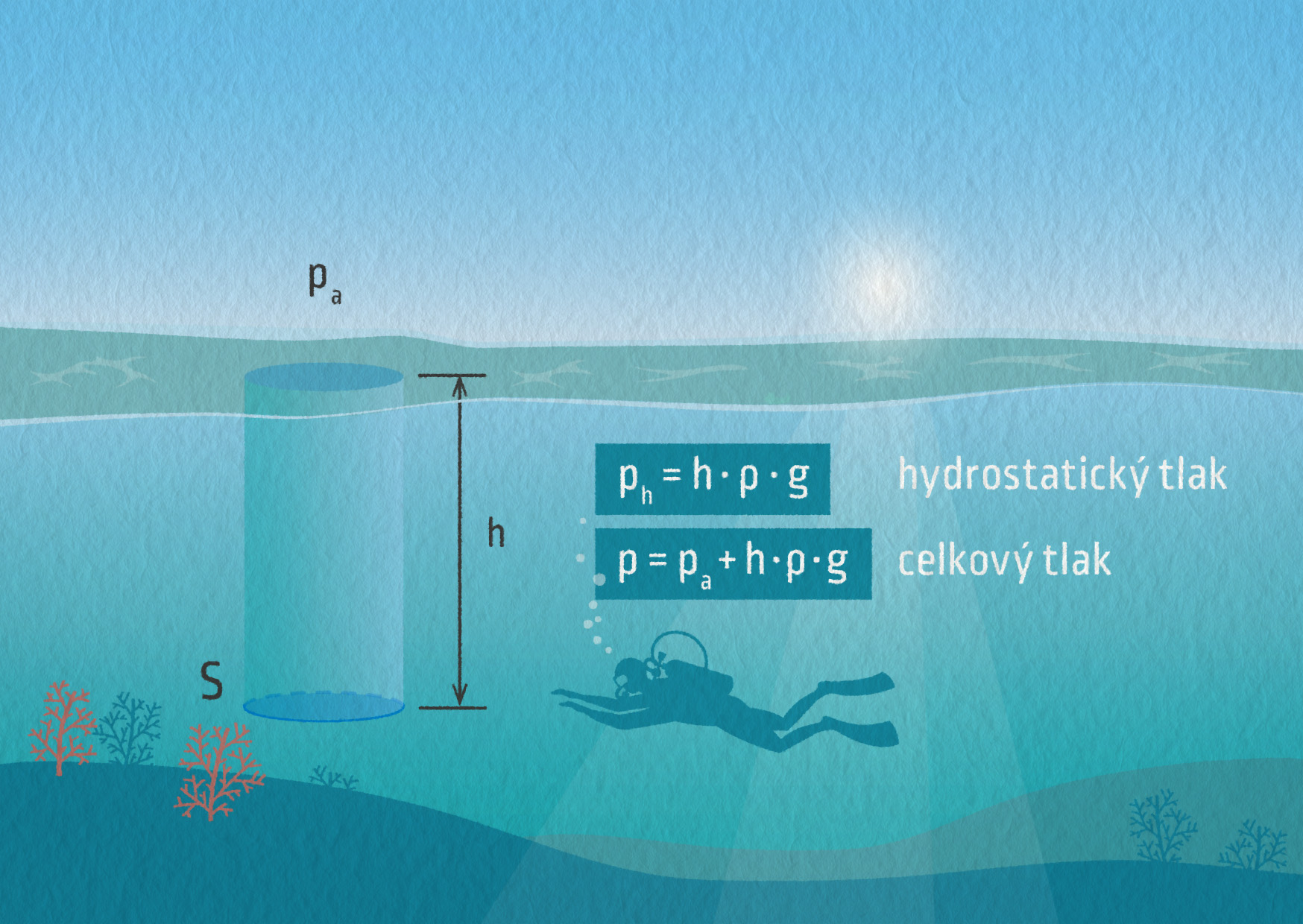
Tlak v tekutině nemusí vznikat jen působením vnější tlakové síly. Pokud je tekutina v gravitačním poli, působí na ni gravitační síla a ta vyvolává v tekutině hydrostatický tlak. V případě kapaliny, kterou můžeme považovat za nestlačitelnou, je situace docela jednoduchá. Jsme-li v určité hloubce \(h\) pod hladinou, je hydrostatický tlak dán gravitační silou \(F_\mathrm{G}=mg\) působící na kapalinu o hustotě \(\varrho\), která se nachází nad námi (viz obrázek):
\[ p_\mathrm{H} = \frac{F_\mathrm{G}}{S} = \frac{mg}{S} = \frac{V\varrho g}{S} = \frac{Sh\varrho g}{S} = h\varrho g \]Uvážíme-li navíc, že nad hladinou je ještě atmosférický tlak \(p_\mathrm{A}\) a ten se dle Pascalova zákona přenáší kapalinou, dostaneme pro celkový tlak v hloubce h:
Celkový tlak v hloubce h pod hladinou je
\(p=p_\mathrm{A}+h\varrho g\)
kde \(h\varrho g\) je hydrostatický tlak a \(p_\mathrm{A}\) atmosférický tlak.
Zdroj
Držitelem světového rekordu ve freedivingu (potápění bez přístrojů) je Alexej Molchanov z Ruska. V disciplíně potápění se závažím dosáhl hloubky 130 m pod hladinou moře.
- Jakému hydrostatickému tlaku bylo vystaveno jeho tělo?
- Jakou tlakovou silou působila voda na každý cm2 jeho těla?
a) \(p=h\varrho g = 130\cdot 1025\cdot 9,8\ \mathrm{Pa}= 1{,}3\ \mathrm{MPa} = 13\ \mathrm{bar}\).
b) \(F=pS = 1{,}3\cdot10^{6}\ \mathrm{Pa}\cdot 10^{-4}\ \mathrm{m}^2 = 1300\ \mathrm{N}\).
Více o fyzice potápění se dočtete v motivačním článku.
Z uvedeného vzorce dále vyplývá, že rozdíl tlaků mezi dvěma hloubkami vypočítáme snadno jako \(\Delta p = \Delta h\varrho g\). Můžeme tak snadno spočítat, že platí:
Rozdíl výšek 1 m vodního sloupce: \(\Delta p = 1{,}0\cdot 9{,}8\cdot 1000\ \mathrm{Pa} = 9{,}8\ \mathrm{kPa} = 10\ \mathrm{kPa}\).
Rozdíl výšek 1 mm rtuťového sloupce: \(\Delta p = 0{,}001\,00\cdot 9{,}81\cdot 13\,595\ \mathrm{Pa} = 133\ \mathrm{Pa} = 1\ \mathrm{torr}\) (starší jednotka tlaku).
Atmosférický tlak
Zemská atmosféra dosahuje výšky asi 100 km. Pod „hladinou“ tohoto plynného tělesa musí být tlak, podobně jako je pod hladinou moře. Jeho velikost však nemůžeme jednoduše vypočítat podle vzorce \(p=h\varrho g\), protože plyn je velmi dobře stlačitelný a jeho hustota s výškou klesá. Pak jsou tu další vlivy jako změny teploty a vlhkosti vzduchu. Jak tedy můžeme změny tlaku v tomto vzdušném oceánu popsat?
- Pokud není rozdíl výšek příliš velký, můžeme použít pro přibližný výpočet rozdílu tlaků vzorec \(\Delta p = \Delta h\varrho g\) a dosadit hustotu vzduchu platnou v daných podmínkách. Například při tlaku 1 bar a teplotě 20 °C je hustota vzduchu 1,2 kg/m3. Pak nám vyjde pro rozdíl výšek 1 m: \(\Delta p=1\cdot 9{,}8\cdot 1{,}2\ \mathrm{Pa}=12\ \mathrm{Pa}\).
- Závislost tlaku na nadmořské výšce je možné popsat pomocí exponenciální funkce (kterou lze odvodit pomocí vyšší matematiky): \[ p_\mathrm{A} = p_0 \mathrm{e}^{-\frac{\varrho_0}{p_0}gz} \]
\(z\) je nadmořská výška, \(p_0\) je tlak v nulové výšce (na hladině moře). Dohodou je tato hodnota stanovena jako normální atmosférický tlak \(p_0=101{,}3\ \mathrm{kPa}\). \(\varrho_0\) je podobně hustota vzduchu v nulové výšce (přibližně 1,2 kg/m3), \(\mathrm{e}=2{,}718\) je Eulerovo číslo (matematická konstanta). Lepší představu o poklesu tlaku s výškou získáme, pokud si tuto funkci vykreslíme do grafu. Tento model už odpovídá realitě velmi dobře, přesto nepostihuje změny tlaku v důsledku pohybu vzduchových hmot s rozdílnou teplotou a vlhkostí. Tyto změny tlaku jsou velmi důležité v meteorologii.

Zdroj
Pomocí vzorce pro tlak vzduchu doplňte hodnoty tlaku v kPa pro různé vrcholy. Počítejte s \(p_0=100\ \mathrm{kPa}\) a \(\varrho_0=1{,}2\ \mathrm{kg/m}^3\).
| Vrchol | Nadmořská výška (m.n.m.) | Tlak (kPa) |
|---|---|---|
| Petřín | 324 | |
| Sněžka | 1602 | |
| Mt. Blanc | 4808 | |
| Mt. Everest | 8849 |
| Vrchol | Nadmořská výška (m.n.m.) | Tlak (kPa) |
|---|---|---|
| Petřín | 324 | 96 |
| Sněžka | 1602 | 83 |
| Mt. Blanc | 4808 | 56 |
| Mt. Everest | 8849 | 35 |
Pokles atmosférického tlaku s výškou má některé praktické důsledky, o kterých je dobré vědět. V předchozím příkladu jsme viděli, že už ve výšce Mt. Blancu je atmosférický tlak zhruba poloviční oproti hladině moře. Přestože koncentrace kyslíku ve vzduchu se nemění, s tlakem klesá také jeho celkové množství v daném objemu vzduchu, který vdechujeme do plic. Proto má naše tělo ve větších nadmořských výškách problémy se zásobováním kyslíkem a to se projevuje jako výšková nemoc. Drobné problémy jako zadýchávání se můžete pociťovat ve výškách už kolem 2 500 metrů. Ve větších výškách pak hrozí bolest hlavy, zvracení a celková slabost. Pokud v případě těchto problémů člověk nesestoupí dolů, ale naopak pokračuje ve výstupu, hrozí smrtící otok plic či mozku. Zajímavé je, že naše tělo si na menší množství kyslíku časem zvykne. Tomu se říká aklimatizace na výšku, která je nezbytná při pobytu ve vysokých horách. S poklesem tlaku musí počítat také konstruktéři letadel, která se pohybují ve výškách okolo 10 km. S poklesem tlaku a hustoty sice klesá odpor vzduchu, ale také vztlak na křídlech. Kromě toho musí být trup letadla vyztužen, aby odolal rozdílu tlaků uvnitř a vně. S poklesem tlaku se ale můžete setkat i při obyčejné jízdě lanovkou nebo rychlým výtahem, kdy vám v důsledku rychlé tlakové změny „zalehnou uši“. Pomocí atmosférického tlaku je rovněž možné měřit nadmořskou výšku. Podrobněji se o tom dočtete v následujícím oddílu.

Zdroj
Někdy může být užitečné snížit tlak v určitém prostoru – vytvořit podtlak. A není nutné kvůli tomu stoupat do velké nadmořské výšky. Podtlak umíme vytvářet pomocí speciálních čerpadel; nejjednodušším z nich je obyčejný vysavač. Na principu podtlaku pracuje také sací pumpa. V technické praxi se zařízení, které slouží k vytváření velkého podtlaku, nazývá vývěva. Onen prostor, v němž je tlak plynu podstatně nižší než atmosférický, pak označujeme jako vakuum. Číselnou představu o různých druzích vakua nabízí následující tabulka.
| Tlak | Počet částic na cm3 | |
|---|---|---|
| zemská atmosféra na hladině moře | 105 Pa | 2,5 ⋅ 1019 |
| běžný vysavač | 0,75 ⋅ 105 Pa | 1,9 ⋅ 1019 |
| atmosféra Marsu (na povrchu planety) | 800 Pa | 2 ⋅ 1017 |
| školní rotační olejová vývěva | 10 Pa | 2,5 ⋅ 1015 |
| atmosféra Měsíce | 3 ⋅ 10−10 Pa | 75 000 |
| turbomolekulární vývěva (limit) | 10−10 Pa | 25 000 |
Poznámka: počet molekul na cm3 je počítán při teplotě 20 °C (výpočet si můžete ověřit sami – viz stavová rovnice).
Podtlak v praxi

Zdroj

Zdroj

Zdroj

Zdroj
Měření tlaku
Tlak je jednou z veličin, se kterými se často setkáváme v každodenním životě (více v galerii). Než se seznámíme s nejdůležitějšími způsoby jeho měření, musíme zmínit rozdíl mezi absolutním a relativním tlakem.
absolutní tlak = tlak měřený vůči vakuu (nulovému tlaku)
relativní tlak (přetlak/podtlak) = tlak měřený vůči atmosférickému (okolnímu) tlaku.
Ve většině případů měříme relativní tlak. Pokud například napumpujete pneumatiku kola tlakem 3 bary, znamená to, že celkový tlak v pneumatice bude 4 bary.
Jaký je absolutní tlak v hloubce 2 m pod hladinou vody? Napište hodnotu v barech.
Kapalinový manometr
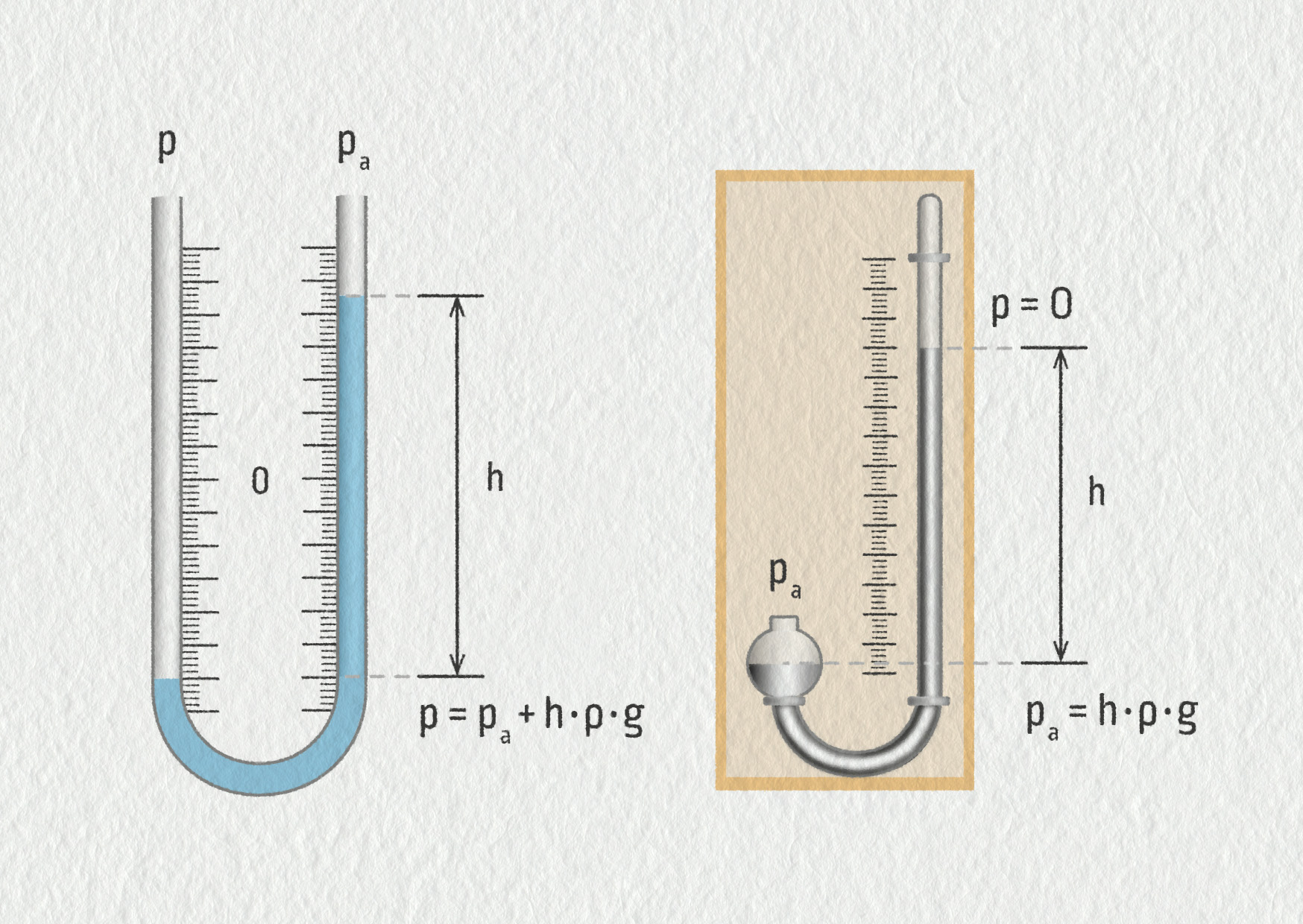
Nejstarší způsob měření tlaku je pomocí trubice naplněné kapalinou, kdy porovnáváme měřený tlak s hydrostatickým tlakem vybrané kapaliny. Pokud necháme oba konce trubice otevřené (viz obrázek a), budeme měřit relativní tlak. Takto funguje například klasický lékařský manometr pro měření krevního tlaku. Trubice je naplněna rtutí kvůli její větší hustotě (1 mm rtuťového sloupce odpovídá tlaku 133,3 Pa = 1 torr). Pokud vám lékař naměří tlak 120/80, znamená to, že maximum vašeho krevního tlaku je 120 torrů = 16 kPa (relativně vůči atmosférickému tlaku).
Zdroj
Pokud jeden konec trubice naplníme kapalinou a uzavřeme, bude tlak plynu na této straně trubice nulový (viz obrázek b). Přesněji: bude zde pouze tlak syté páry kapaliny, což je pro rtuť za pokojové teploty méně než 1 Pa. Rtuťový barometr byl vynalezen Evangelistou Torricellim v roce 1643. Od té doby začali lidé měřit a sledovat změny atmosférického tlaku. Vy si můžete Torricelliho pokus vyzkoušet s vodou v rámci motivační aktivity.
Deformační manometr
Kapalinový manometr není příliš praktické zařízení, neboť kapalina se může vylít, a hlavně pro větší tlakový rozsah je potřeba dlouhá trubice. Proto se tlak nejčastěji měří manometrem s Bourdonovou trubicí (viz obrázek). Jeho základ tvoří dutá kovová zatočená trubice, která se při zvětšení tlaku mírně rozevře (narovná). Tento pohyb je převeden na ručičku doplněnou stupnicí.

Zdroj
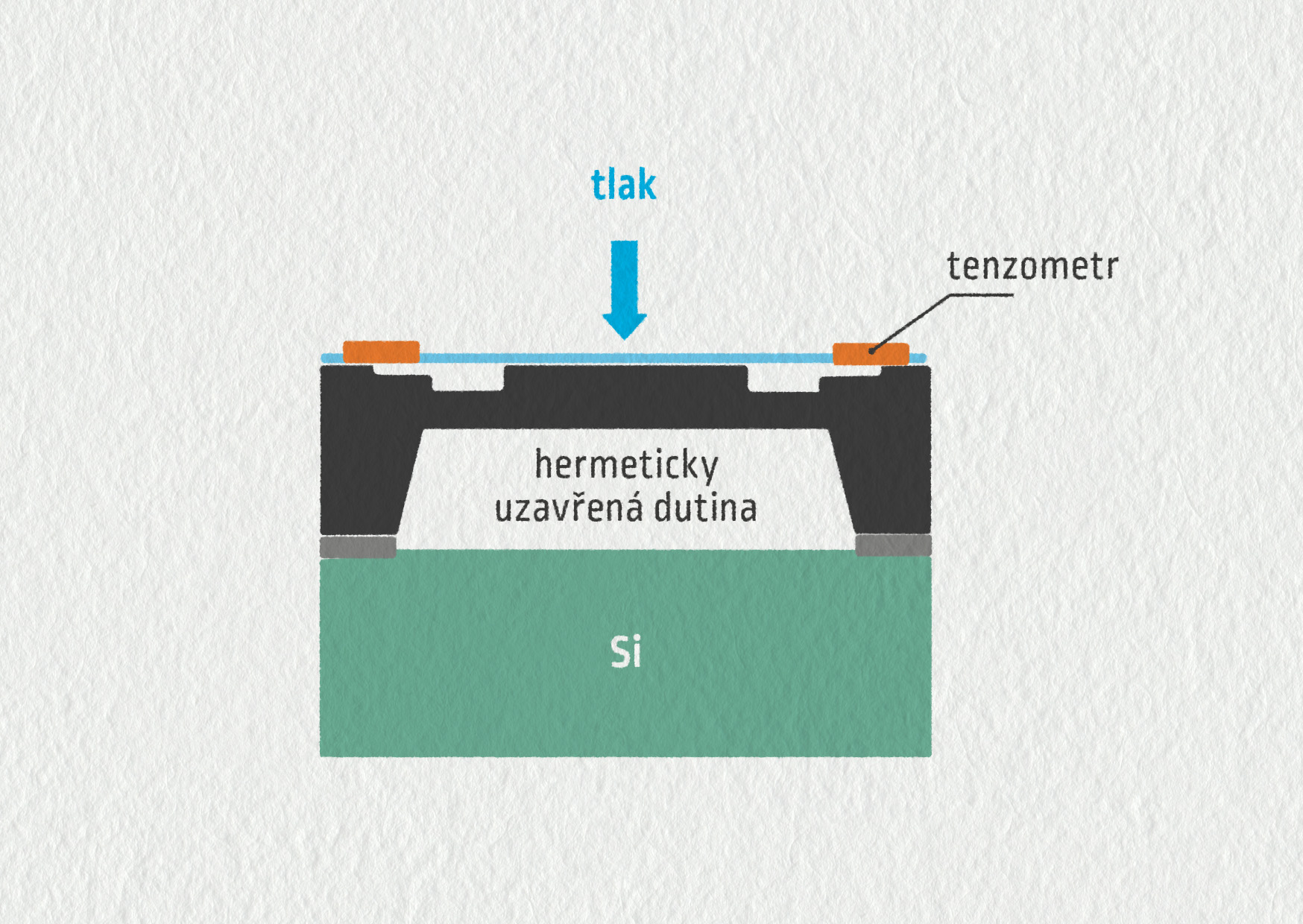
Membránový senzor tlaku
V digitální době máme samozřejmě možnost měřit tlak také pomocí elektronického senzoru. Existuje několik způsobů konstrukce a zapojení. Nejčastěji se jedná o miniaturní dutinu vyplněnou vakuem (případně plynem o známém tlaku). Při změnách tlaku se jedna stěna dutiny nepatrně deformuje a to je převáděno na elektrické napětí pomocí tenzometru. Tento senzor tlaku může bez problému sloužit také jako barometr v meteostanicích nebo jako výškoměr s citlivostí na metry.
Zdroj
Měření tlaku

Zdroj
Zdroj

Zdroj

Zdroj

Zdroj

Zdroj

