Pojďme se podrobněji podívat na vlastnosti plynných těles. Můžeme je zkoumat experimentálně při mnoha různých dějích, jako je třeba prudké stlačování vzduchu v pístu (viz obrázek). Při prudkém stlačení vzduchu v pístu vzroste teplota plynu natolik, že dojde ke vzplanutí malého kousku papíru. V řeči fyzikálních veličin můžeme říct, že při rychlém stlačení (zmenšení objemu) dojde k nárůstu tlaku a teploty plynu. Úplně stejný proces probíhá také v pístech spalovacího motoru.

Zdroj
Stav plynu v určitém okamžiku můžeme popsat pomocí tří měřitelných veličin: tlaku \(p\), objemu \(V\) a teploty \(T\). Kromě těchto tří veličin můžeme měřit ještě množství plynu. To můžeme udělat například pomocí počtu částic \(N\), který lze vyjádřit také pomocí látkového množství (\(N=nN_\mathrm{A},\) kde je \(N_\mathrm{A}\) Avogadrova konstanta).
Tyto čtyři veličiny označujeme jako stavové veličiny:
\(p\) = tlak
\(V\) = objem
\(T\) = teplota
\(n\) = látkové množství (nebo \(N\) = počet částic)
Pokud budeme sledovat, co se děje s plynem v pevné uzavřené nádobě, budou dvě ze čtyř stavových veličin (počet částic a objem) neměnné. Tím se situace velmi zjednoduší, neboť budeme moci sledovat, jak se mění tlak v závislosti na teplotě. Jak se plyn ohřívá, roste i jeho tlak. Přesněji to lze vyčíst z grafu (viz obrázek).
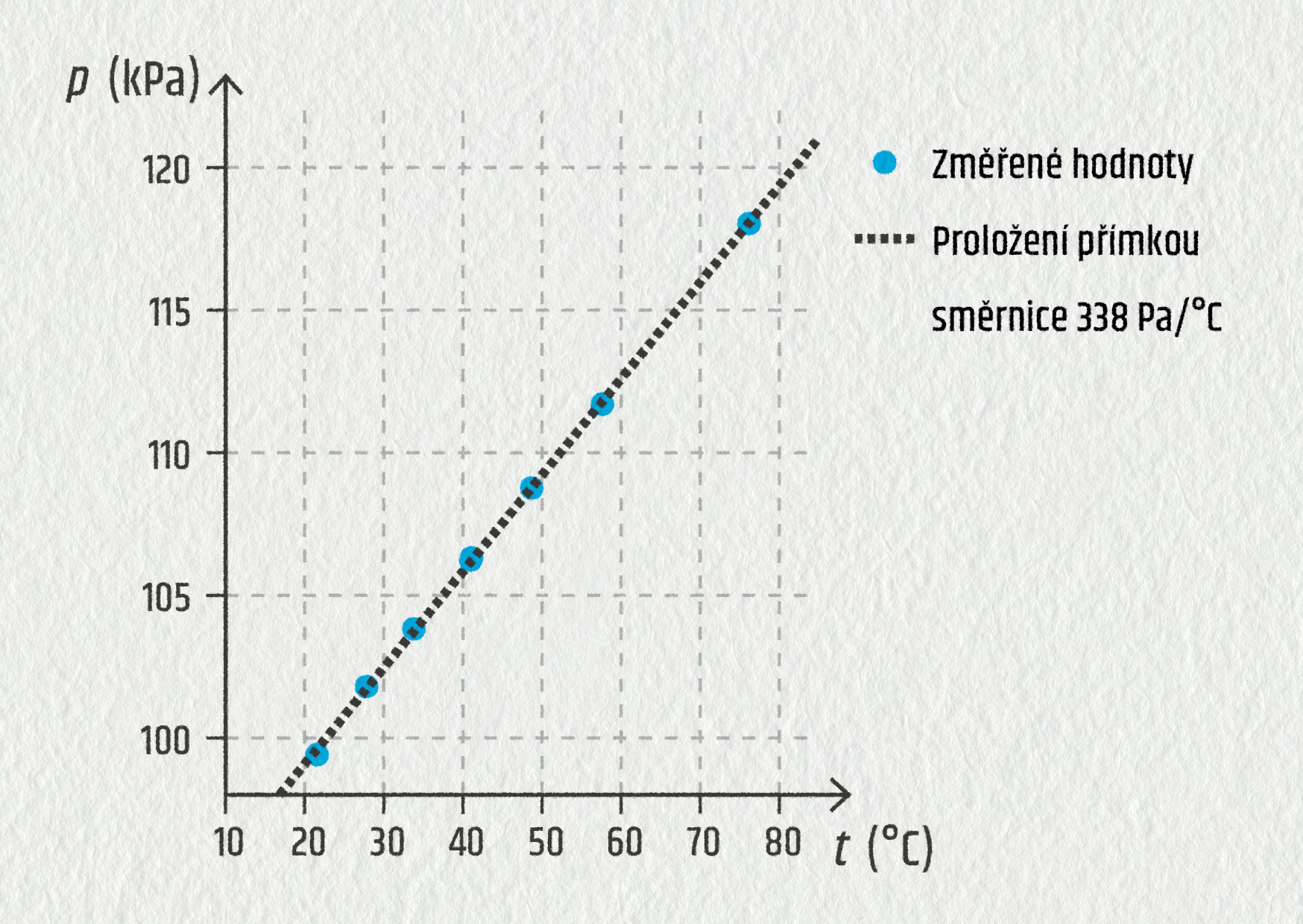
Zdroj
Podobně můžeme sledovat, co se děje s plynem za stálé teploty. Objem měníme velmi pomalu, aby plyn stihl vyrovnávat teplotu s okolím. Zjistíme, že při zmenšení objemu roste tlak plynu. Tentokrát nám z grafu vyjde nepřímá úměrnost (viz obrázek).
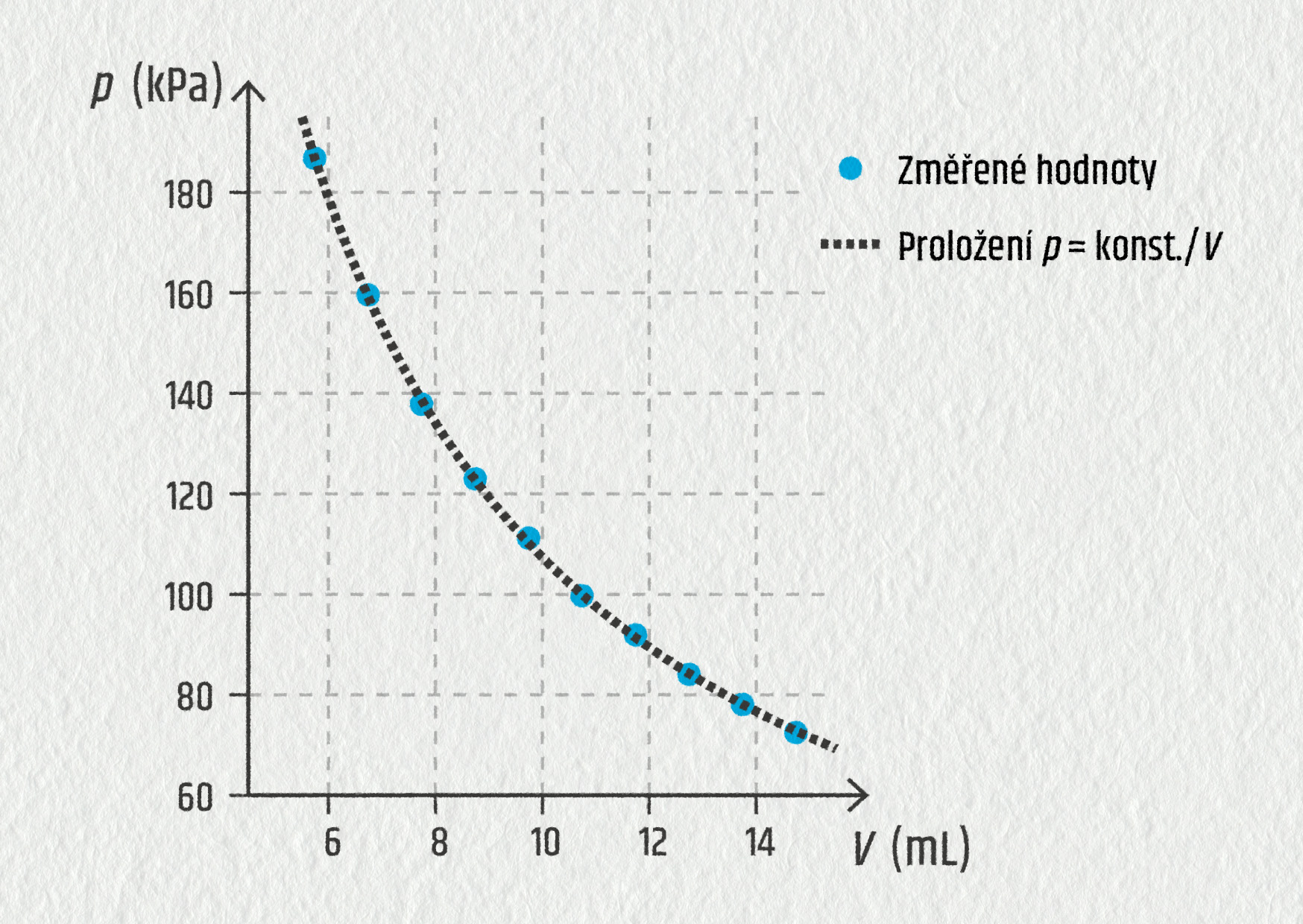
Zdroj
Podobná měření prováděli fyzikové převážně v průběhu 18. století a postupně experimentálně odvodili vztah mezi stavovými veličinami pro konkrétní množství plynu (vy si tyto experimenty můžete sami vyzkoušet v praktiku). Z těchto měření vyplývá, že tlak je přímo úměrný teplotě a nepřímo úměrný objemu plynu. To můžeme zapsat pomocí neznámé konstanty (značíme ji zkratkou konst) jako \(p=\mathrm{konst.}\cdot T/V\). Odtud vyplývá, že výraz \(pV/T\) se musí rovnat neznámé konstantě:
\[ \frac{pV}{T} = \mathrm{konst.} \]Zdůrazněme, že se jedná o termodynamickou teplotu (v Kelvinech), proto ji značíme velkým písmenem \( \mathrm{T} \).
Tento vztah mezi stavovými veličinami se nazývá stavová rovnice ideálního plynu. V modelu ideálního plynu považujeme molekuly plynu za kuličky zanedbatelného objemu, které se mohou srážet dokonale pružnými srážkami. Tlak plynu pak vysvětlíme nárazy kuliček (molekul) na stěny nádoby. Trochu složitější je souvislost teploty a rychlosti pohybu částic, o které si můžete přečíst v rozšiřující poznámce souvislost teploty a energie.
Stavovou rovnici ideálního plynu je možné odvodit také teoreticky a můžeme ji zapsat ve dvou různých tvarech. Oba říkají to samé, ale pomocí jiných veličin. Při počítání si pak můžeme vybrat, který tvar se nám lépe hodí.
Stavová rovnice ideálního plynu:
\(pV=NkT\), \(k=1{,}381\cdot 10^{-23}\ \mathrm{J}\cdot \mathrm{K}^{-1}\) je Boltzmannova konstanta
\(pV=nRT\), \(R= kN_\mathrm{A} = 8{,}314\ \mathrm{J}\cdot \mathrm{K}^{-1}\cdot \mathrm{mol}^{-1}\) je univerzální plynová konstanta
V reálných plynech budeme vždy pozorovat menší či větší odchylky od tohoto jednoduchého modelu. Přesnější popis nabízí van der Waalsova stavová rovnice, která zohledňuje skutečnost, že nelze zanedbat vlastní objem částic, a také to, že přitažlivé síly mezi částicemi ovlivňují jejich pohyb. Za normálních podmínek (tlak 1 bar, teplota 0 °C) je náš model velmi přesný, neboť molekuly zaujímají řádově jen 0,1 % prostoru a rovněž vliv mezimolekulových sil je zanedbatelný.
Teplota je veličina, která je na mikroskopické úrovni spojena s vnitřní kinetickou energií částic. Jinými slovy je teplota dána tím, jak rychle se částice pohybují. Problém je v tom, že částice se pohybují chaoticky, jejich rychlosti jsou různé. Proto je potřeba rychlosti částic správným způsobem zprůměrovat. Pro ideální plyn lze odvodit jednoduchý vztah pro střední kinetickou energii jedné molekuly plynu
\[ E_1 = \frac{3}{2} kT \]Právě tímto způsobem se ve stavové rovnici objevila Boltzmannova konstanta \(k\). Pokud navíc rozepíšeme kinetickou energii, dostaneme
\[ \frac{1}{2}m_1v_1^2 = \frac{3}{2}kT \]a odtud
\[ v_1 = \sqrt{\frac{3kT}{m_1}} \]Rychlost \(v_1\) označujeme jako střední kvadratickou rychlost částic ideálního plynu. Všimněte si, že kromě teploty zde hraje roli i hmotnost částic (atomů, molekuly). Lehčí částice proto mají při stejné teplotě vyšší rychlosti.
Použití stavové rovnice
Stavová rovnice obsahuje kompletní informace o plynném tělese. Prakticky ji tedy můžeme použít pro výpočet čtvrté stavové veličiny při znalosti zbylých tří. Ukázku najdete v řešeném příkladu.
Italský fyzik Amedeo Avogadro zveřejnil roku 1811 hypotézu, že všechny plyny obsahují ve stejné objemové jednotce při stejném tlaku a teplotě stejný počet molekul. V jeho době však zůstala hypotéza prakticky bez povšimnutí, nebo byla dokonce odmítána. Avogadro totiž nedokázal hypotézu přesně experimentálně ověřit. Dnes toto tvrzení nazýváme Avogadrův zákon a můžeme ho formulovat přesněji: 1 mol libovolného plynu zaujímá za normálních podmínek (tlak 1 bar, teplota 0 °C) objem 22,4 l. Odvoďte Avogadrův zákon pomocí stavové rovnice.
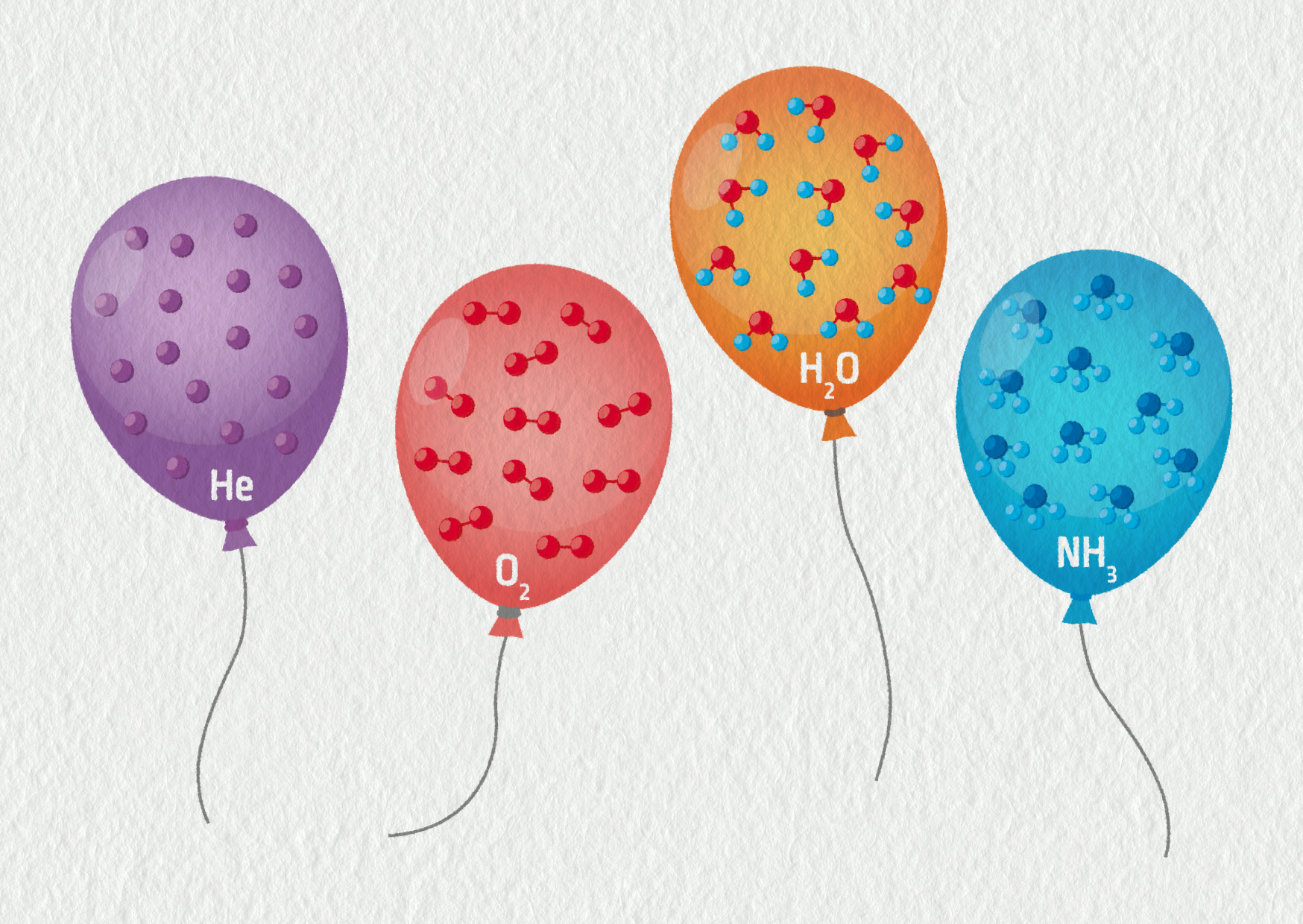
Zdroj
Ze stavové rovnice ve tvaru \(pV=nRT\) vyjádříme objem a dosadíme všechny hodnoty v základních jednotkách:
\[ V = \frac{nRT}{p} = \frac{1\cdot 8{,}3\cdot 273}{101\,300}\ \mathrm{m}^2 = 0{,}0224\ \mathrm{m}^3 = 22{,}4\ \mathrm{l} \]Další možností použití stavové rovnice je porovnání dvou různých stavů konkrétního plynného tělesa (N je konstantní). Pak můžeme napsat rovnici ve tvaru
Pokud je navíc některá z veličin \(p\), \(V\), \(T\) neměnná, její hodnota na obou stranách rovnice je stejná, a můžeme ji zkrátit. Například pro děj, který probíhá za stálé teploty, bude platit
\[ \frac{p_1V_1}{T_1} = \frac{p_2V_2}{T_2}\;,\quad T_1=T_2=T \quad\Rightarrow\quad \frac{p_1V_1}{T} = \frac{p_2V_2}{T} \quad\Rightarrow\quad p_1V_1 = p_2V_2 \quad\Rightarrow\quad pV=\mathrm{konst.} \]Speciální děje, při kterých je stálá hodnota jedné stavové veličiny, mají své názvy. Můžeme je přehledně zapsat do následující tabulky.
| izotermický děj | stálá teplota \(T\) | \(pV = \mathrm{konst.}\) |
| izochorický děj | stálý objem \(V\) | \(p/T = \mathrm{konst.}\) |
| izobarický děj | stálý tlak \(p\) | \(V/T = \mathrm{konst.}\) |
Konkrétní použití uvidíme v řešených příkladech.
Pokud zapomenete nafouknutý gumový člun na přímém slunci, může se stát, že tlak v lodi se nebezpečně zvýší a loď se může poškodit. Vypočítejte, jak vzroste tlak v lodi, která byla nafouknutá přetlakem 0,20 bar, pokud se teplota vzduchu v lodi zvýšila z 25 °C na 75 °C. Objem nafouknuté lodi se nemění.
Objem již nafouknuté lodi se nemění, proto \(V=\mathrm{konst.}\) a platí
\[ \frac{p_1}{T_1} = \frac{p_2}{T_2} \]Odtud
\[ p_2 = \frac{T_2}{T_1}p_1 = \frac{348\ \mathrm{K}}{298\ \mathrm{K}}\cdot1{,}20\ \mathrm{bar} = 1{,}40\ \mathrm{bar} \]Přetlak proto vzroste o 0,2 bar na 0,4 bar.
Všimněte si, že teplotu jsme dosazovali v kelvinech. Pokud by někdo tvrdil, že teplota stoupla na trojnásobek (z 25 °C na 75 °C), nemá jeho tvrzení fyzikální smysl, protože Celsiova stupnice umožňuje i záporné hodnoty teploty.
V létě roku 1982 se Američan Larry Walters zapsal do dějin, když uskutečnil 45minutový let v zahradním křesle neseném pomocí 45 meteorologických balónů plněných heliem. Při svém letu dosáhl maximální výšky zhruba 4 600 m a nakonec se mu podařilo bezpečně přistát na pevnině, což lze považovat za velké štěstí. Meteorologický balón je vyroben z velmi pružného materiálu, a může tak snadno zvětšovat svůj objem.
- Odhadněte, o kolik procent vzroste objem balónu ve výšce 4600 m oproti nulové startovní výšce. Teplota na zemi je 20 °C, teplota ve výšce 4 600 m je −3 °C.
- Některé meteorologické balóny dokážou vystoupat až do výšky kolem 25 km, kde prasknou a malá sonda s přístrojovým vybavením pak spadne zpět na padáku. Vysvětlete, proč balón ve velké výšce praskne.
a) Při řešení nesmíme zapomenout na pokles atmosférického tlaku s výškou. Pro výšku 4600 m vychází tlak 56 kPa (viz graf pro závislost tlaku na výšce). Vidíme, že v tomto případě se mění teplota, tlak i objem. Proto použijeme rovnici ve tvaru
\[ \frac{p_1V_1}{T_1} = \frac{p_2V_2}{T_2} \]Odtud
\[ V_2 = \frac{p_1T_2}{p_2T_1}V_1 = \frac{101\cdot270}{56\cdot293}\cdot V_1 = 1{,}66V_1 \]Ať už byl původní objem \(V_1\) jakýkoliv, můžeme říci, že objem vzrostl na 1,66 násobek neboli o 66 %.
b) Tlak ve výšce 25 km je už jen cca 4 kPa. Objem balónu by tak měl vzrůst cca dvacetinásobně (závisí také na teplotě). Tak velkou pružnost však stěny balónu nemají.
Rovnice se jmenuje na počest svého objevitele, kterým byl nizozemský fyzik Johannes Diderik van der Waals (1837–1923). V roce 1910 obdržel za svůj objev Nobelovu cenu za fyziku.
Van der Waalsovu rovnici zapisujeme ve tvaru
\[ \left(p + \frac{n^2a}{V^2} \right) (V-nb) = nRT \]kde \(a\), \(b\) jsou konstanty charakteristické pro daný plyn a jejich hodnoty se stanovují experimentálně. Například pro dusík N2 je \(a=0{,}137\ \mathrm{Pa}\cdot\mathrm{m}^6\cdot\mathrm{mol}^{-2}\), \(b=3{,}869\cdot10^{-5}\cdot\mathrm{m}^3\cdot\mathrm{mol}^{-1}\). Všimněte si, že pro \(a=b=0\) se korekční členy vynulují a dostaneme obyčejnou stavovou rovnici ideálního plynu.

