Nabitá tělesa svojí přítomností ovlivňují vlastnosti okolního prostoru – vytvářejí kolem sebe elektrické pole. Pokud se do takového pole dostane jiné nabité těleso nebo nabitá částice, bude na ni působit elektrická síla \(\Vec{F}_\mathrm{e}\). Říkáme, že elektrické pole má silové účinky. Elektrické pole zprostředkovává působení mezi náboji na dálku.
Jak znázornit elektrické pole?
Podobně jako u gravitačního pole můžeme elektrické pole znázornit pomocí siločar. Siločára je křivka, která v každém místě ukazuje směr elektrické síly, která by působila na kladný testovací náboj. Přesněji řečeno, vektor \(\Vec{F}_\mathrm{e}\) má směr tečny k siločáře. V obrázku 18.18 je nakresleno elektrické pole vytvořené kladnou a zápornou kuličkou. Všimněte si, že siločáry začínají na kladném tělese a končí na záporném.
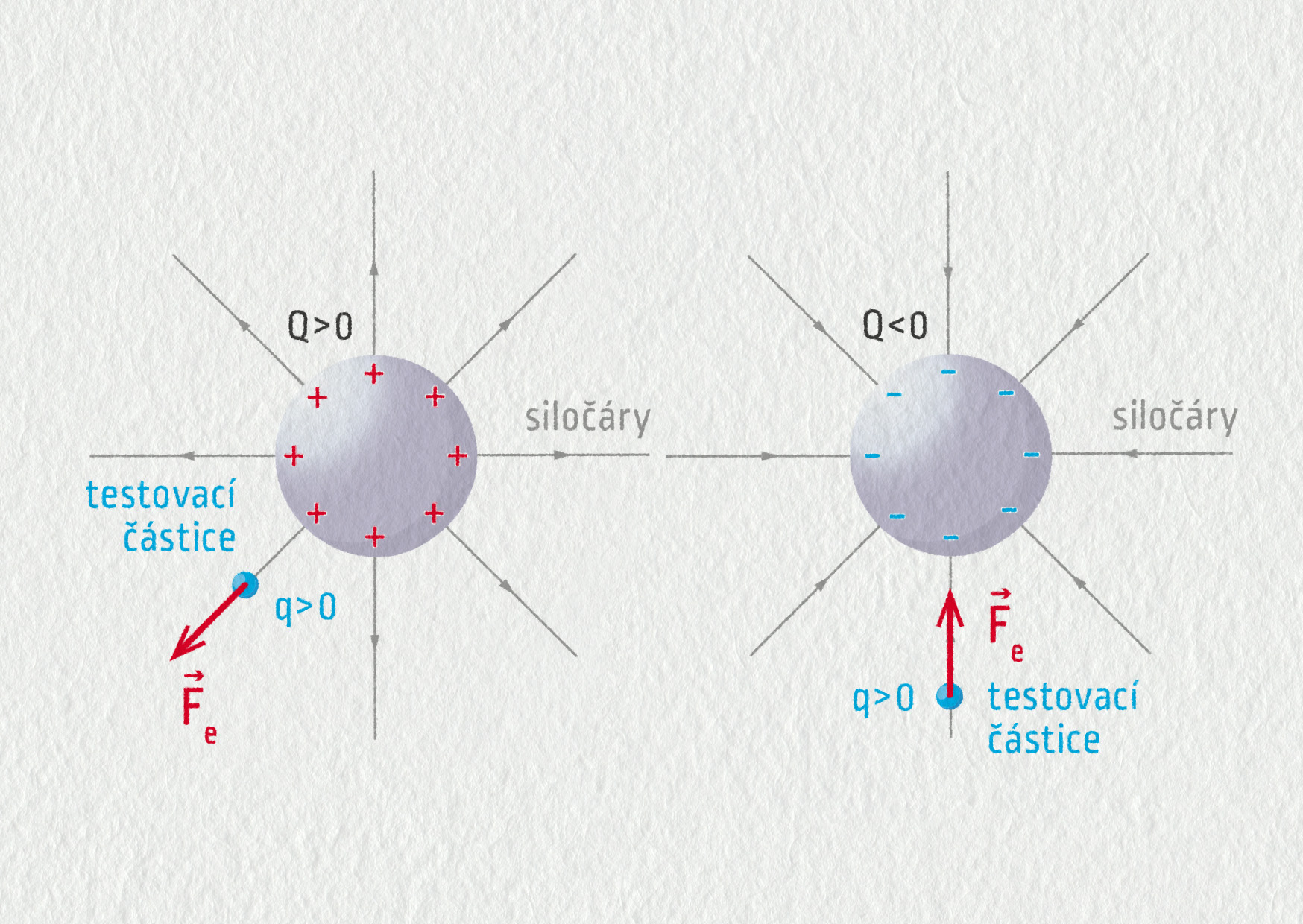
Zdroj
V centrálním elektrickém poli se siločáry paprsčitě rozbíhají nebo sbíhají. Takové pole existuje např. v okolí nabité částice nebo rovnoměrně nabité kuličky. V homogenním poli jsou siločáry rovnoběžné – toto pole má ve všech místech stejné vlastnosti. V prostoru mezi dvěma rovnoběžnými nabitými deskami vzniká téměř homogenní elektrické pole. Dokonale homogenní by bylo v případě nekonečně douhých desek.
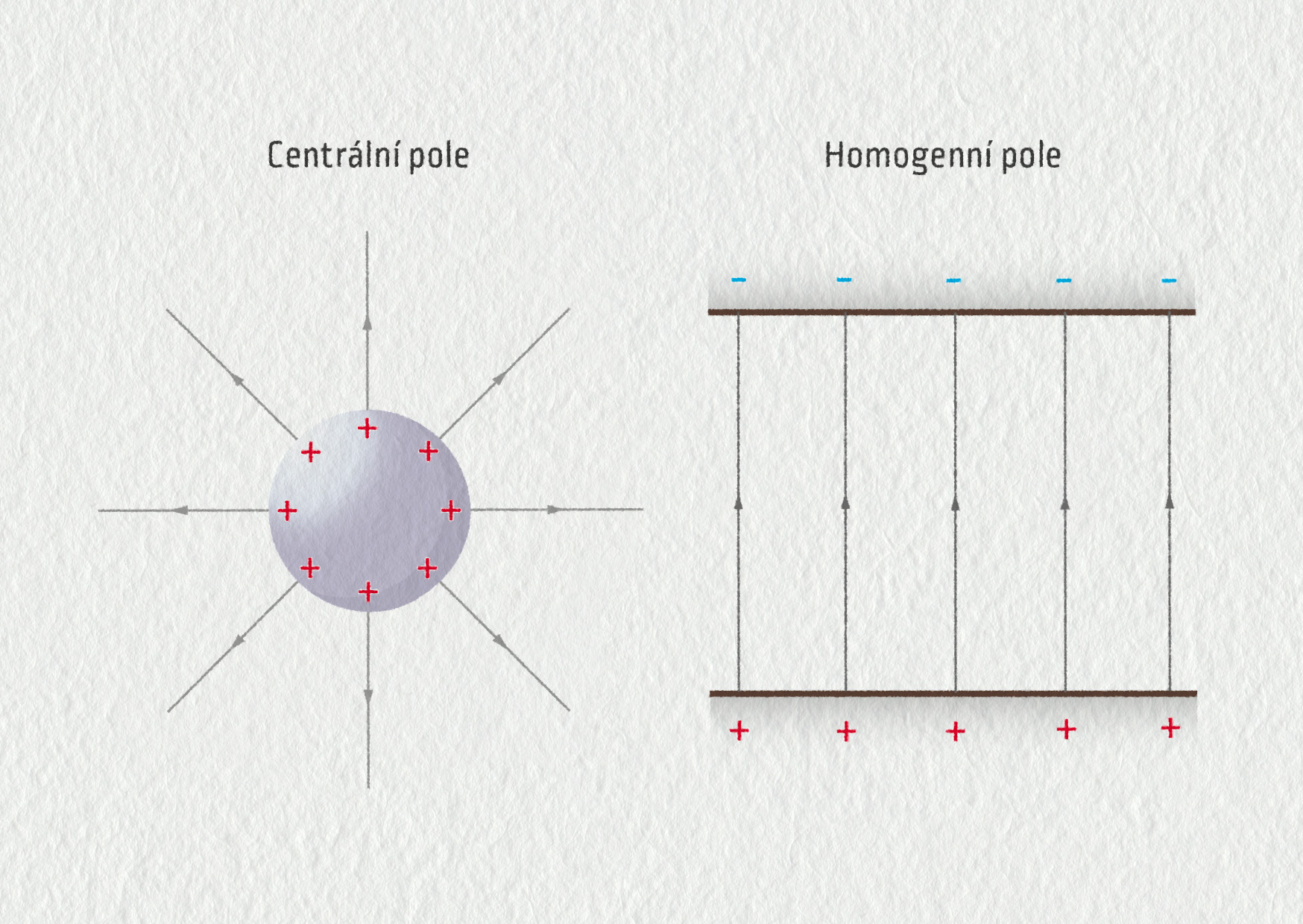
Zdroj
Intenzita elektrického pole
Zatímco siločáry dávají dobrou představu o směru pole, je obtížné z nich přesně určit, jak je pole v daném místě „silné“. Obě zmíněné vlastnosti – směr a „sílu pole“ – v sobě zahrnuje vektorová fyzikální veličina intenzita elektrického pole \(\Vec{E}\). Je definována vztahem
\[ \Vec{E} = \frac{\Vec{F}_\mathrm{e}}q\;, \]kde \(\Vec{F}_\mathrm{e}\) je elektrická síla působící na náboj \(q\) v určitém místě pole. Jednotkou intenzity elektrického pole je N/C.
Vektor \(\Vec{E}\) má vždy směr tečny k siločáře. Elektrická síla \(\Vec{F}_\mathrm{e}\) je vždy rovnoběžná s intenzitou pole \(\Vec{E}\).
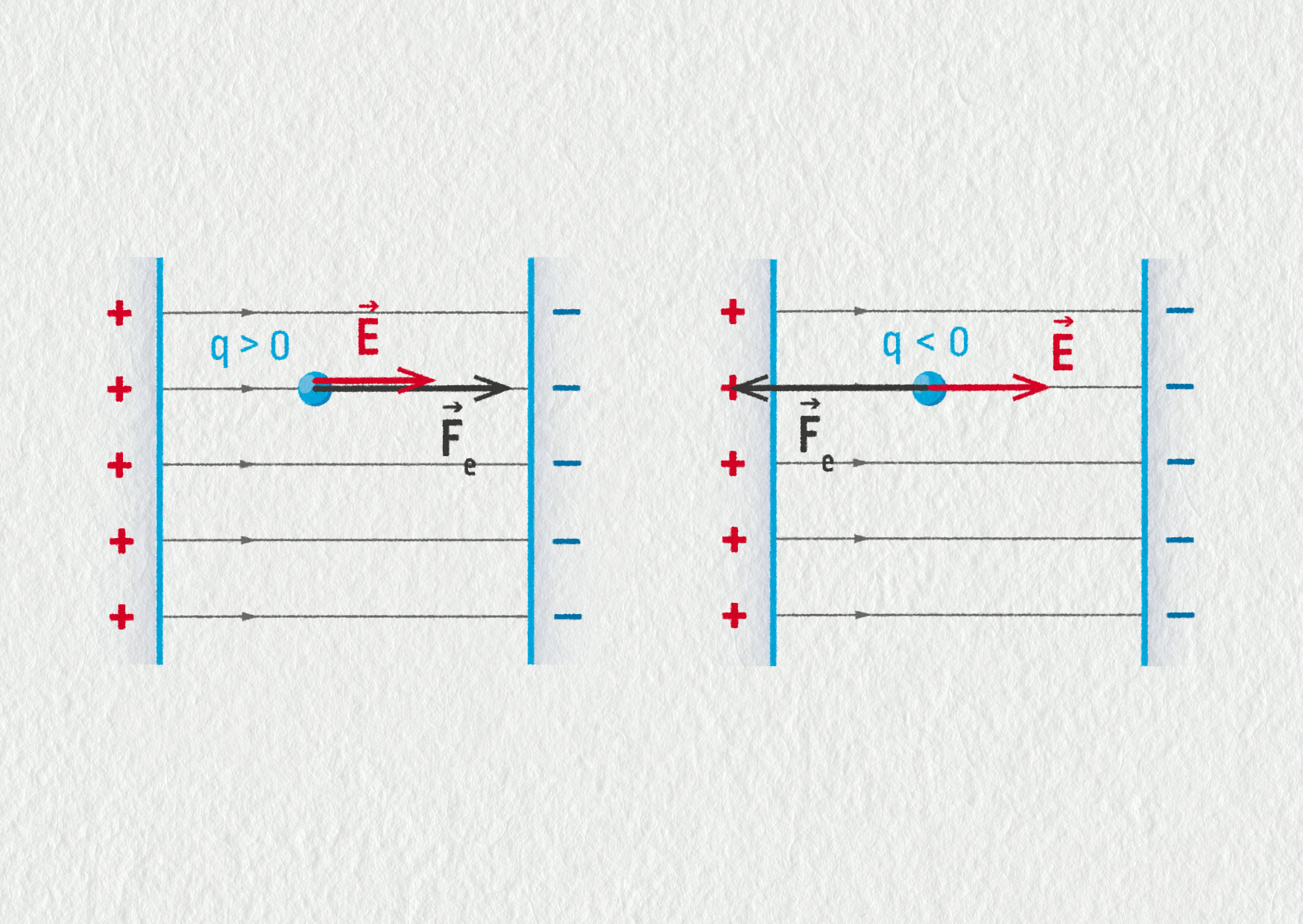
Zdroj
Pokud má částice nacházející se v poli kladný náboj, jsou \(\Vec{F}_\mathrm{e}\) a \(\Vec{E}\) souhlasně orientované. Pokud je náboj částice záporný, působí síla proti směru intenzity pole.
V případě centrálního pole lze velikost intenzity pole vypočítat z Coulombova zákona:
\[ E = \frac{F_\mathrm{e}}q = \frac{\displaystyle k\frac{|qQ|}{r^2}}{q} = k\frac{|Q|}{r^2}\;. \]Vidíme tedy, že pole slábne kvadraticky s rostoucí vzdáleností od nabitého tělesa.
V případě homogenního pole má intenzita elektrického pole \(\Vec{E}\) ve všech místech stejný směr i velikost. V následujícím oddílu ukážeme, že v poli vytvořeném mezi dvěma rovinnými deskami je velikost intenzity pole \(E=U/d\), kde \(d\) značí vzdálenost desek a \(U\) napětí mezi nimi. Proto se někdy jako jednotka intenzity používá V/m.
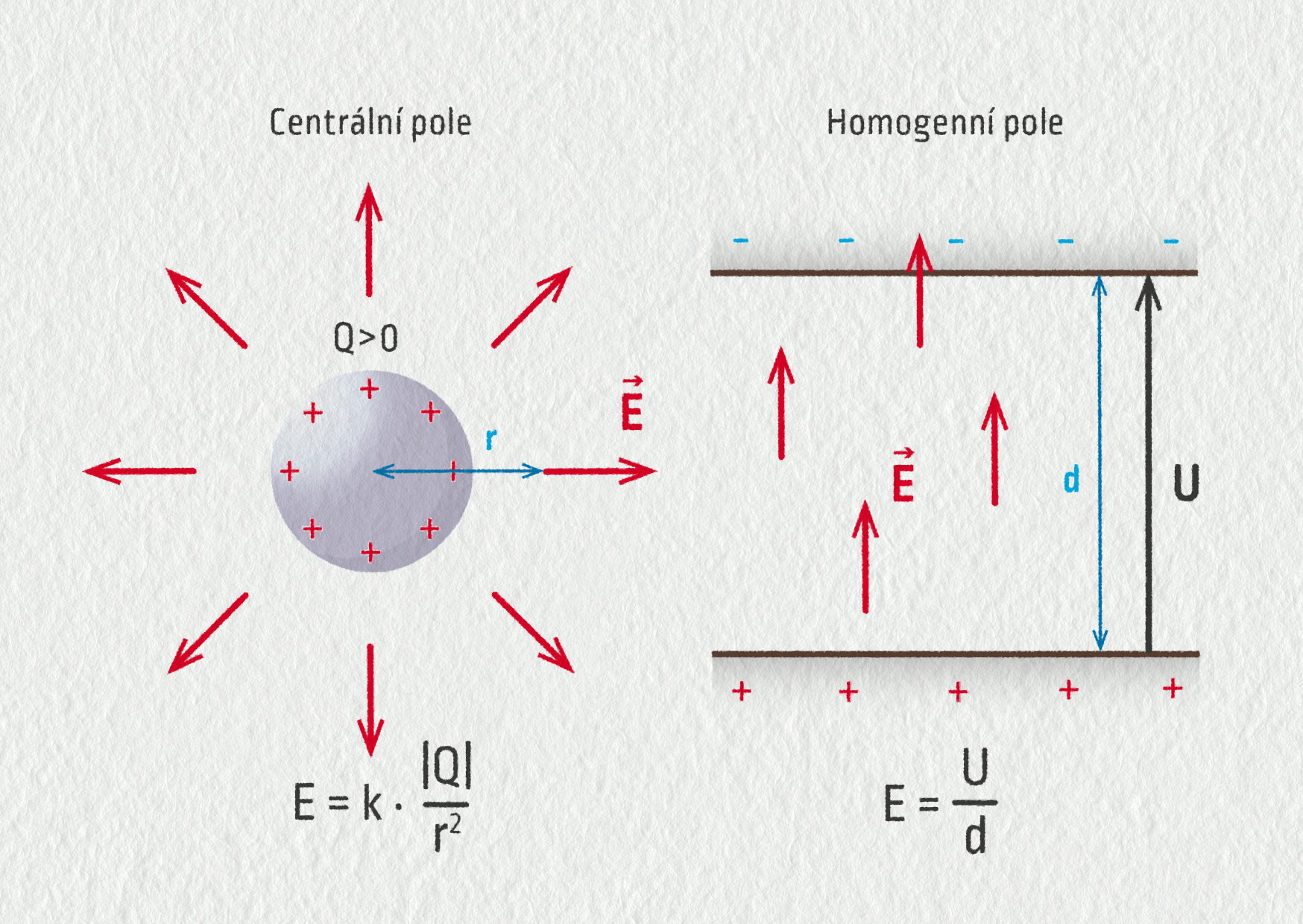
Zdroj
Do určitého bodu v prostoru může zasahovat elektrické pole vytvořené větším počtem nabitých těles (těleso 1 vytváří pole o intenzitě \(\Vec{E}_1\), těleso 2 vytváří pole o intenzitě \(\Vec{E}_2\) atd.). Výsledné pole v tomto bodě je pak vektorovým součtem jednotlivých intenzit: \(\Vec{E}=\Vec{E}_1+\Vec{E}_2+\dots\).
\(\Vec{F}_\mathrm{e}\) leží na tečně k siločáře. Pokud je \(q<0\), jsou siločára a \(\Vec{F}_\mathrm{e}\) opačně orientované.
Elektrické pole existuje nejen v prázdném prostoru nebo ve vzduchu kolem nabitých těles. Nejčastěji je vytváříme záměrně v elektrických obvodech. Zdroj připojený do obvodu vytváří ve vodičích a součástkách elektrické pole, které elektrickou silou působí na nabité částice v tomto obvodu, a ty se dávají do pohybu: vzniká elektrický proud. Třebaže se informace o připojení zdroje (čili elektrické pole) obvodem šíří rychlostí elektromagnetických vln (rychlostí řádově 108 m/s), elektrony v kovech se ke kladnému pólu zdroje posouvají velmi pomalu (rychlostí řádově 1 mm/s).
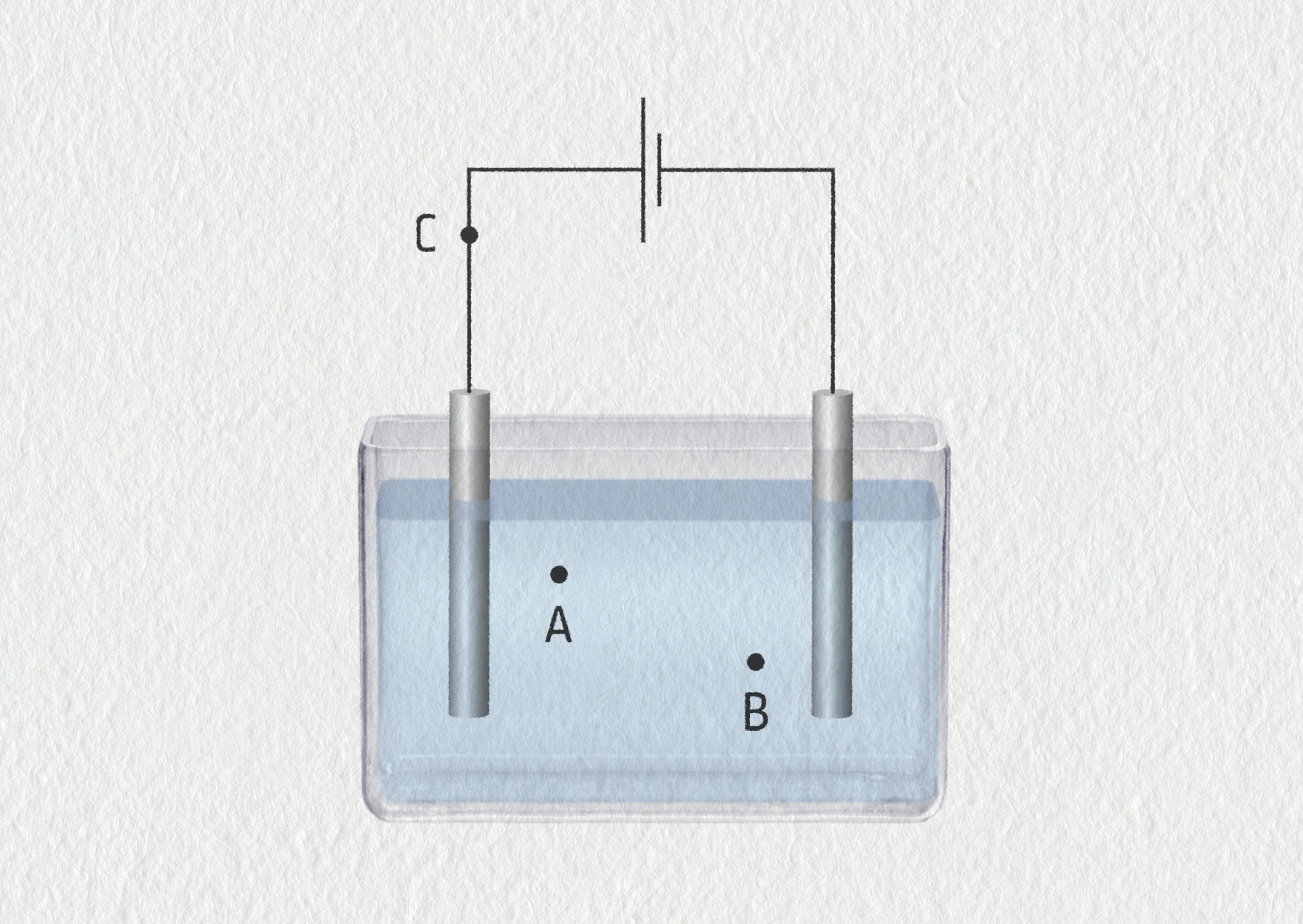
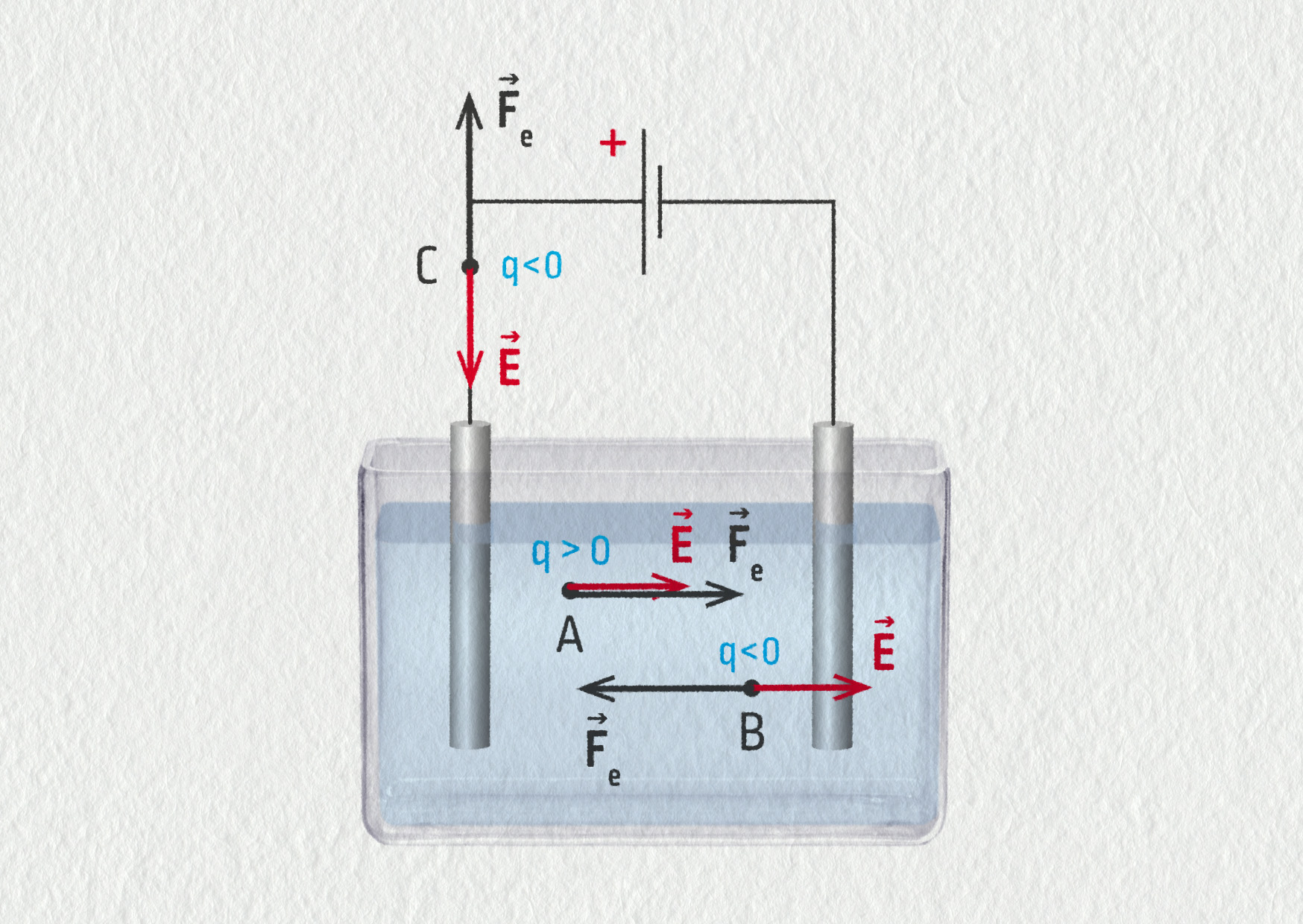
V roztoku modré skalice jsou ponořeny dvě elektrody a ty jsou připojeny ke stejnosměrnému zdroji. Na obrázku 18.23 se v bodě A nachází iont \(\mathrm{Cu}^{2+}\), v bodě B iont \(\mathrm{SO}_4^{2-}\), v bodě C je elektron. Znázorněte směr elektrického pole \(\Vec{E}\) v bodech A, B (v kapalině) a C (v kovovém vodiči) a směr elektrické síly \(\Vec{F}_\mathrm{e}\) působící na příslušnou částici.
Zdroj
Zdroj
Vektor \(\Vec{E}\) směřuje vždy od kladného k zápornému pólu zdroje pole. Pokud je \(q<0\), mají síla \(\Vec{F}_\mathrm{e}\) a pole \(\Vec{E}\) opačnou orientaci.
Elektrické napětí
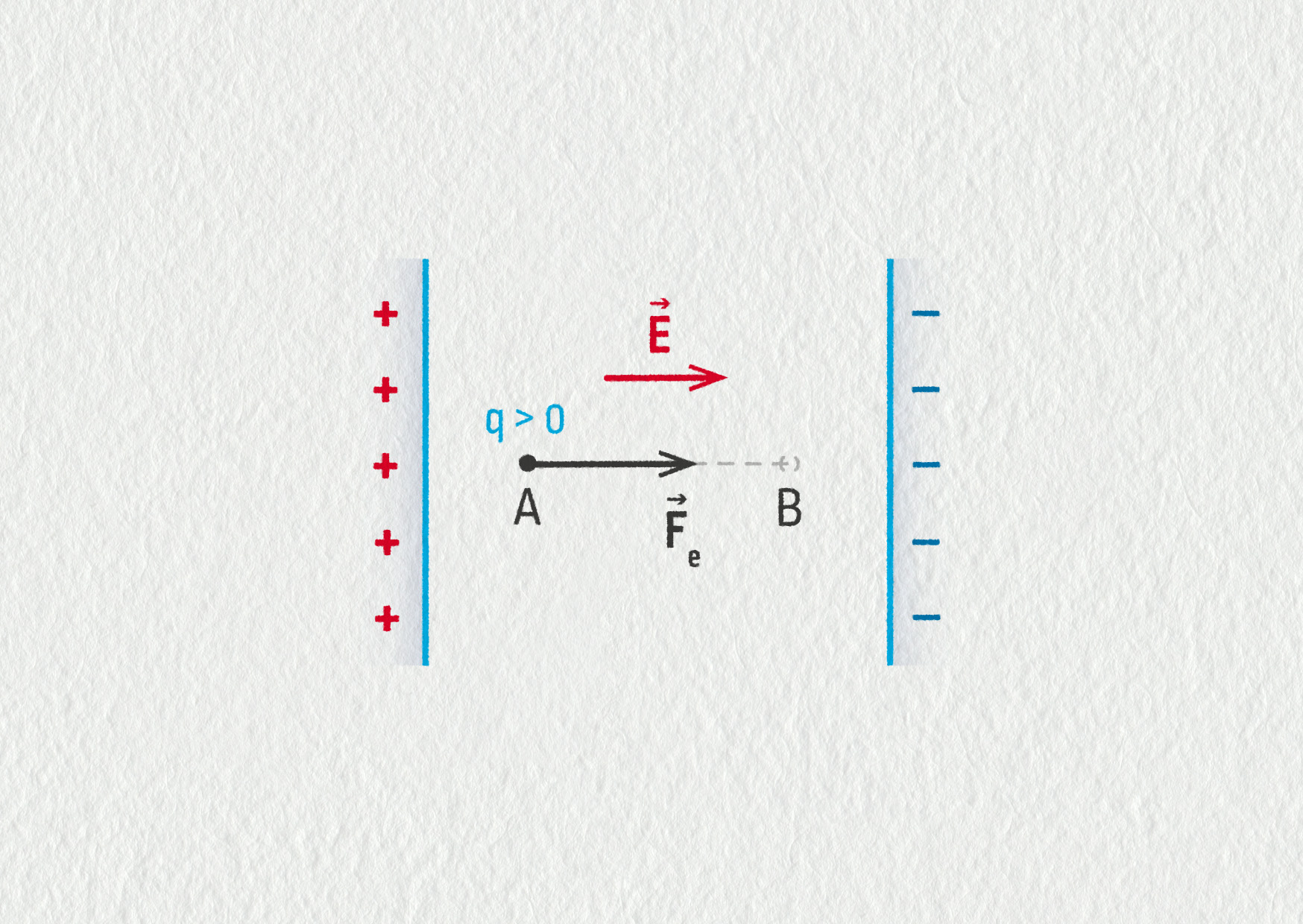
Uvažujme malý testovací náboj \(q>0\) nacházející se v bodě A v homogenním elektrickém poli – viz obrázek 18.25. Působí na něj elektrická síla \(\Vec{F}_\mathrm{e}\) ve směru pole \(\Vec{E}\). Posune-li se náboj z bodu A do bodu B, vykoná elektrická síla práci \(W=F_\mathrm{e}s=qEs\), kde dráha \(s=|AB|\). Pomocí práce elektrické síly je definováno elektrické napětí.
Zdroj
Definice elektrického napětí
Elektrické napětí \(U_{AB}\) je definováno pomocí práce \(W_\mathrm{e}\), kterou vykoná elektrická síla při přenesení náboje \(q\) z bodu A do bodu B.
\[ U_{AB} = \frac{W_\mathrm{e}}q \]Jednotkou napětí je volt V.
Veličina napětí \(U_{AB}\) má oproti elektrické síle a elektrické práci jednu obrovskou přednost: dá se jednoduše měřit. Stačí zapojit voltmetr mezi body A a B a už čteme hodnotu. Více podrobností o znaménku, měření a významu napětí v obvodech najdete v 7. kapitole.
Z definice napětí získáváme užitečný vztah pro výpočet práce elektrické síly:
\[W_\mathrm{e}=qU\]Bude se nám velice hodit k vyjadřování energie urychlených částic.
Zdroj
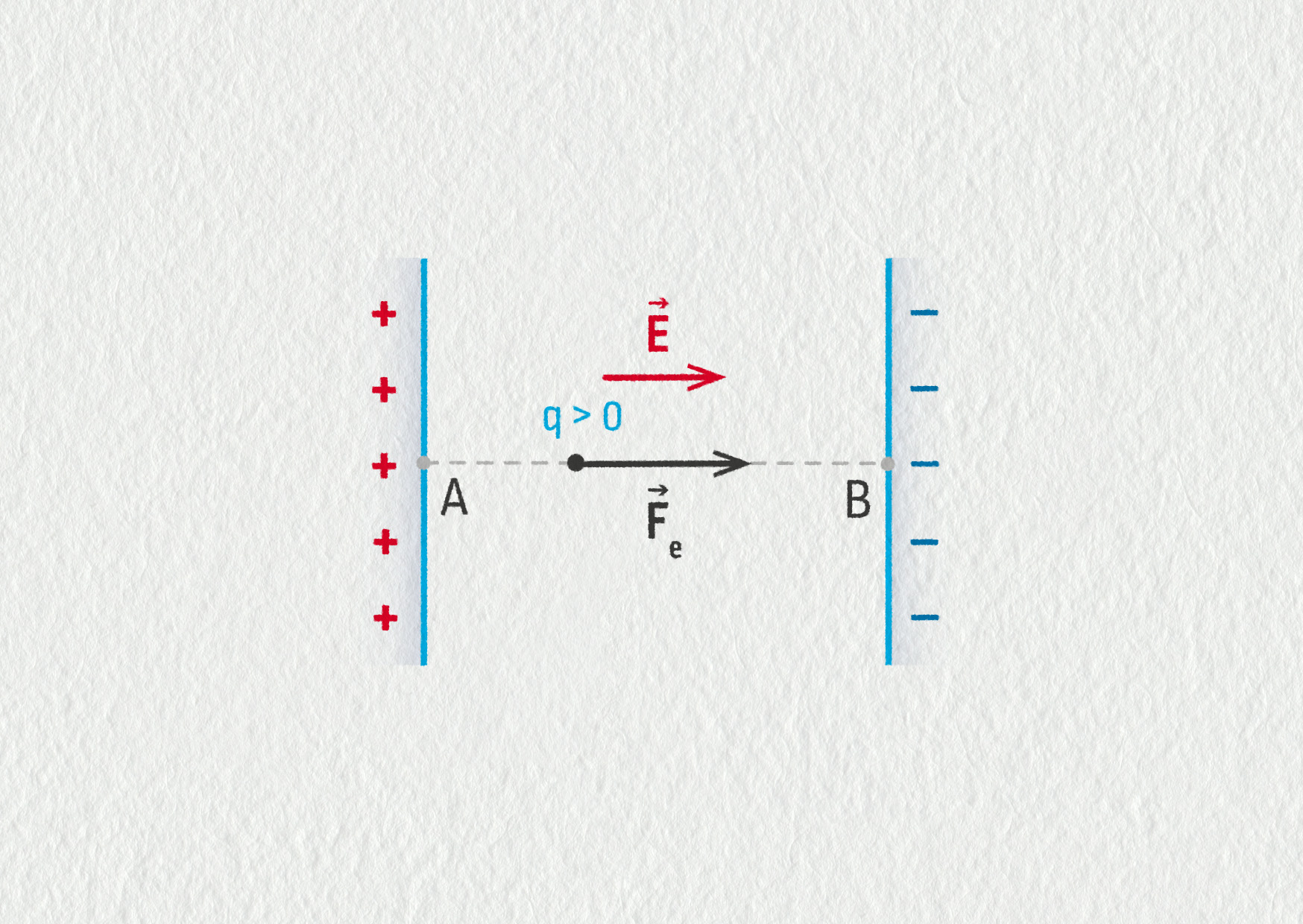
Předpokládejme, že v obrázku 18.26 bod A leží na kladné desce a bod B na desce záporné. Vzdálenost \(|AB|=d\) je zřejmě vzdálenost desek. Práce, kterou vykoná \(\Vec{F}_\mathrm{e}\) při přenesení náboje \(q\) z A do B, je \(W_\mathrm{e}=F_\mathrm{e}d=qEd\). Dosazením \(W_\mathrm{e}=qU\) získáváme \(qU=qEd\), odkud snadno vyjádříme \(E=U/d\). Můžete si všimnout, že jednotkou intenzity elektrického pole je volt na metr čili platí 1 N/C = 1 V/m. Dokázali byste vyjádřit volt pomocí základních jednotek SI?
Elektrická síla \(\Vec{F}_\mathrm{e}\) patří mezi konzervativní síly. Posouvá-li elektrická síla nábojem z A do B, práce \(W_\mathrm{e}\) nezávisí na tom, po jaké trajektorii se náboj z A do B přemístil. Prostě ať jdeme z A do B po úsečce nebo po jiné komplikovanější křivce, práce \(W_\mathrm{e}\) vyjde vždy stejně velká. Tato vlastnost elektrické síly umožňuje zavést potenciální energii.
Definice: Potenciální energie nabité částice v určitém místě elektrického pole je rovna práci, kterou vykoná elektrická síla při přenesení částice z daného místa do referenčního bodu.
Referenční bod je dohodou zvolené místo, kde je potenciální energie nulová. Často se volí neutrální těleso (Země), nebo se klade referenční bod do nekonečna. Aby nedošlo k záměně s vektorovou intenzitou pole \(\Vec{E}\), budeme potenciální energii částice v elektrickém poli značit zdobným písmem \(\mathcal{E}_\mathrm{P}\). Jednotkou \(\mathcal{E}_\mathrm{P}\) je joule J.
Homogenní pole
Zdroj
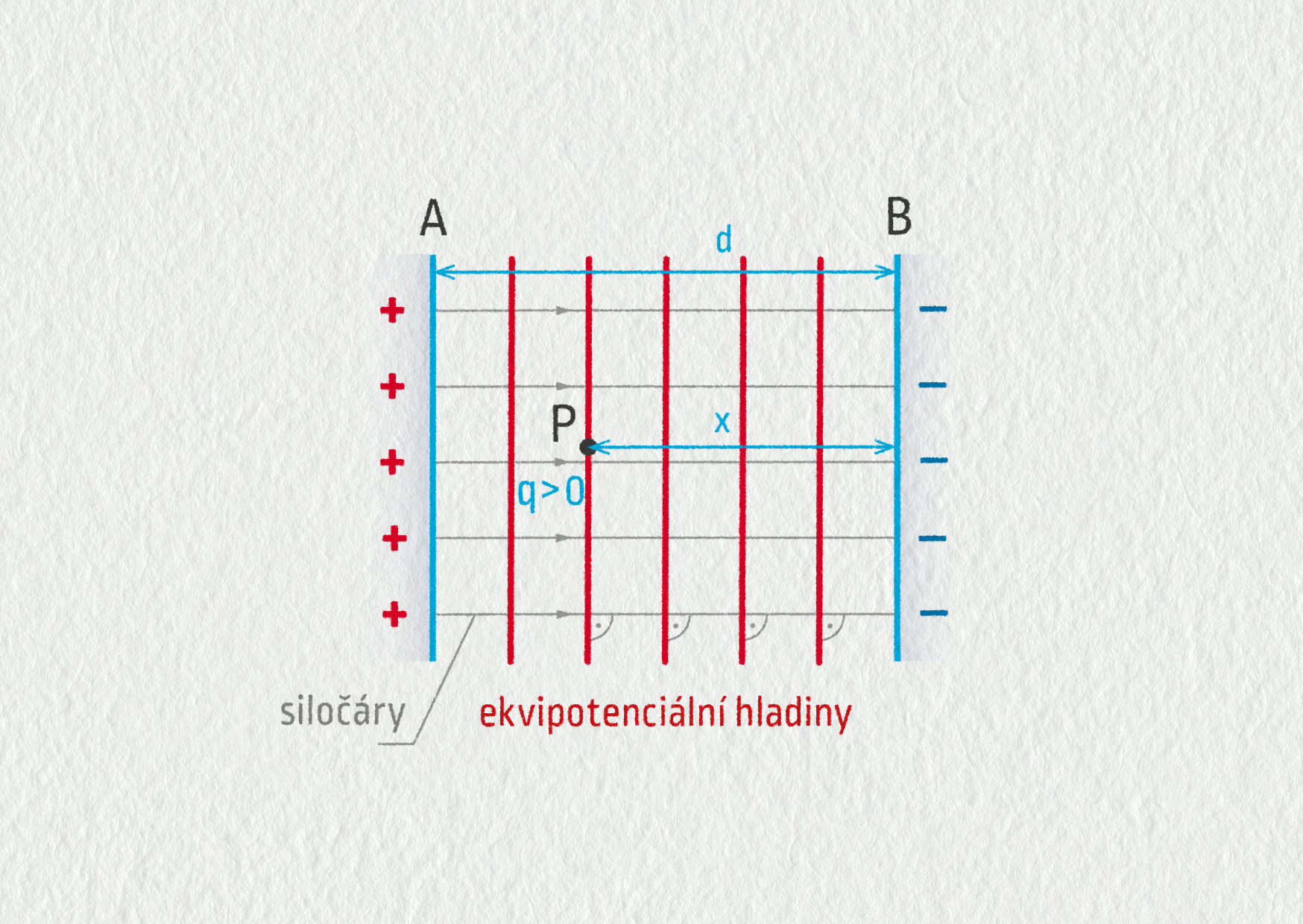
Odvodíme vztah pro potenciální energii částice v homogenním poli. Referenční bod si zvolíme na záporné desce B – viz obrázek 18.27. Potenciální energii \(\mathcal{E}_\mathrm{P}\), kterou má částice s nábojem \(q\) v bodě P homogenního pole, vypočítáme snadno podle definice: je to práce, kterou vykoná elektrická síla při přenesení částice z bodu P na desku B,
\[ \mathcal{E}_\mathrm{P} = W_\mathrm{e} = F_\mathrm{e}x = qEx = q\frac{U_{AB}}dx\;. \]Ekvipotenciální hladiny spojují místa v prostoru, kde má náboj \(q\) stejnou potenciální energii.
V homogenním poli se jedná o rovnoběžné plochy, neboť vzdálenost \(x\) od desky B je v těchto bodech konstantní. Samotné nabité desky A a B jsou rovněž ekvipotenciálními hladinami. Obecně platí, že ekvipotenciální hladiny jsou kolmé na siločáry.
Centrální pole
Spočítáme potenciální energii částice o náboji \(q\) umístěné v poli vytvořeném nábojem \(Q\) ve vzdálenosti \(r\) od centra. Referenční bod zvolíme v nekonečnu. Potenciální energie náboje \(q\) ve vzdálenosti \(r\) od zdroje pole se rovná práci, kterou vykoná elektrická síla \(\Vec{F}_\mathrm{e}\) při přenesení tohoto náboje z \(r\) do nekonečna. Pole je nehomogenní, síla není konstantní a podle Coulombova zákona klesá kvadraticky s rostoucí vzdáleností \(x\). Proto práci musíme počítat integrálem.
\[ \mathcal{E}_\mathrm{P} = W_\mathrm{e} = \int_r^\infty F_\mathrm{e}\,\mathrm{d}x =\] \[=\int_r^\infty k\frac{qQ}{x^2}\,\mathrm{d}x = kqQ\int_r^\infty \frac1{x^2}\,\mathrm{d}x =\] \[= kqQ\left[ -\frac1x \right]_r^\infty =\] \[= kqQ \left[ 0 - \left(-\frac1r\right)\right] = k\frac{qQ}r \]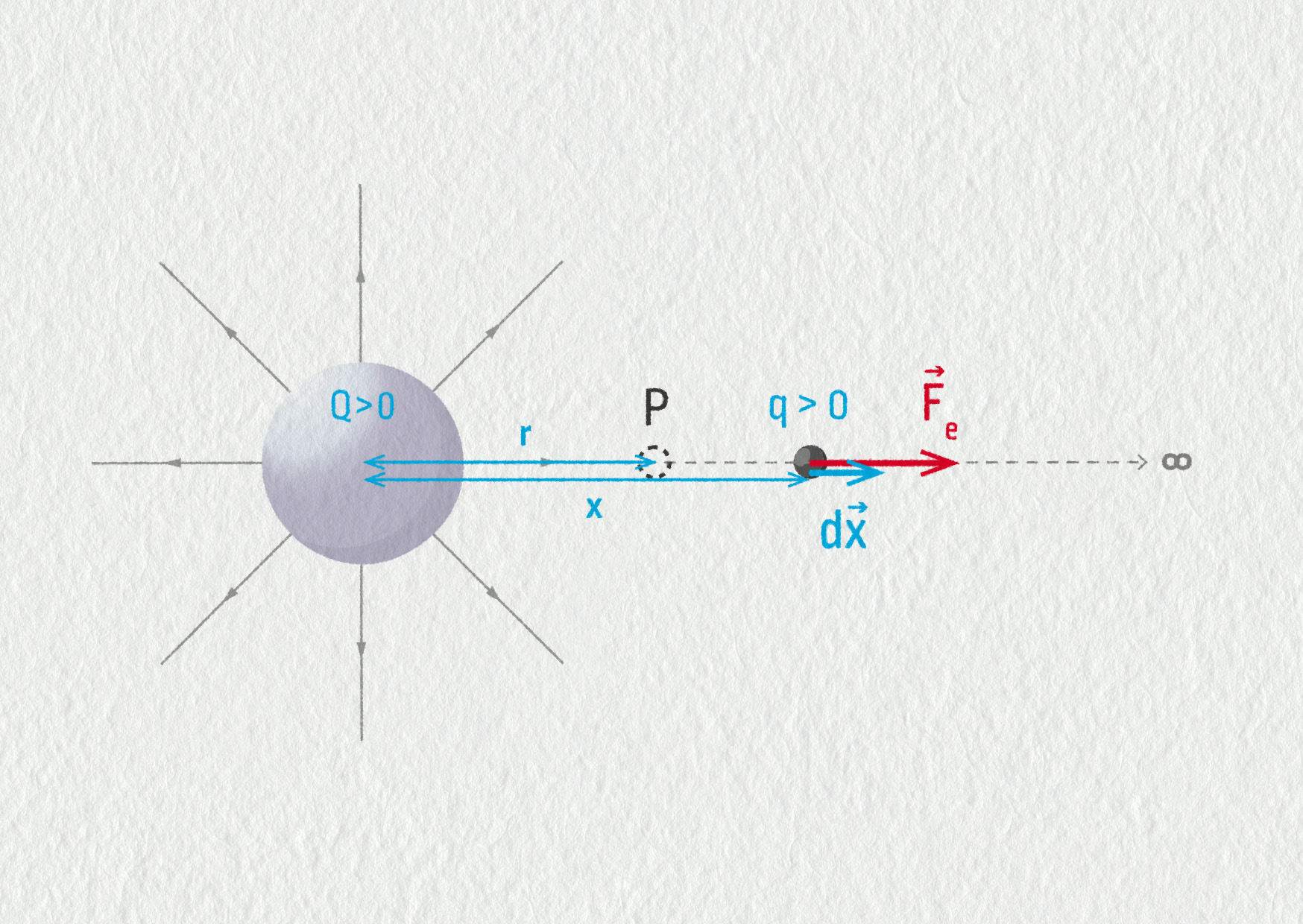
Zdroj
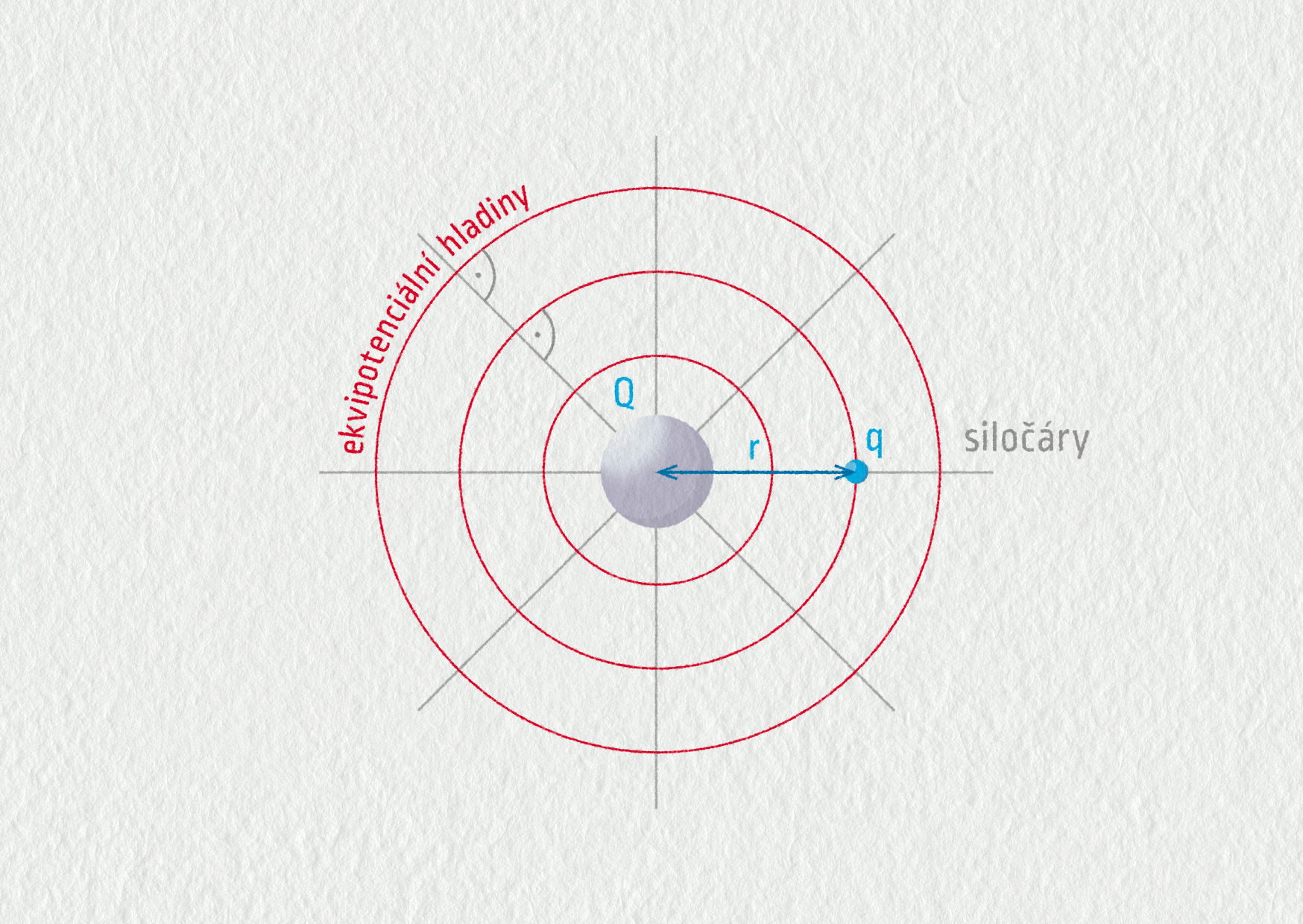
Zjišťujeme, že potenciální energie je nepřímo úměrná první mocnině vzdálenosti. Ekvipotenciální hladiny jsou soustředné kulové plochy. Potenciální energie je záporná, pokud náboje nemají stejné znaménko.
Zdroj
Potenciál a napětí
Na příkladu homogenního a centrálního pole jsme viděli, že potenciální energie \(\mathcal{E}_\mathrm{P}\) závisí na zdroji pole, na poloze částice v něm a na náboji částice samotné. K popisu pole samotného můžeme zavést skalární veličinu elektrický potenciál \(\varphi\) předpisem \(\varphi=\mathcal{E}_\mathrm{P}/q\). Potenciál \(\varphi_A\) je roven potenciální energii, kterou by měl náboj +1 C umístěný v bodě A elektrického pole.
Porovnáním definic potenciálu, potenciální energie a napětí můžeme postřehnout velice zajímavou vlastnost: potenciál \(\varphi_A\) v bodě A je roven elektrickému napětí mezi bodem A a referenčním bodem, kde je potenciál nulový. Prakticky to znamená, že každému bodu prostoru můžeme přiřadit určitou hodnotu ve voltech (potenciál), která nám říká, jakou potenciální energii by v tomto bodě měl náboj +1 C.
Odtud plyne známá vlastnost napětí: Elektrické napětí \(U_{AB}\) je rozdíl potenciálů mezi body A a B:
\[U_{AB}=\varphi_A-\varphi_B\;. \]Příklad
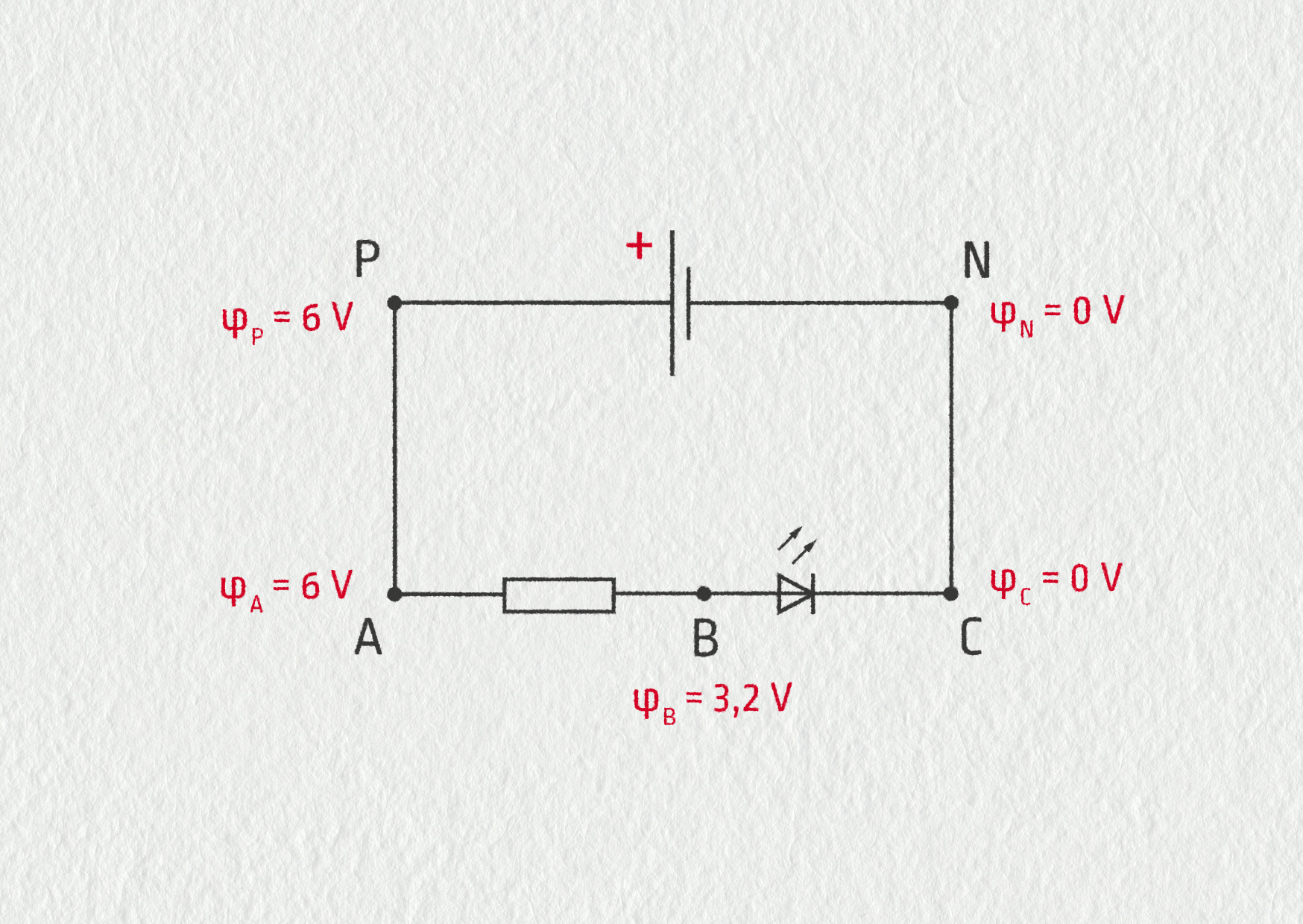
Vyložená teorie platí nejen ve vakuu nebo ve vzduchu, ale také v elektrických obvodech, které už známe. Vezměme například sériový obvod se zdrojem 6 V, rezistorem a modrou svítivou diodou o pracovním napětí 3,2 V a proudu 10 mA. V obvodu si vyznačme body A, B, C, P, N – viz obrázek 18.30.
Zdroj
Jako referenční bod zvolme třeba zápornou svorku zdroje N, tedy potenciál \(\varphi_N=0\ \mathrm{V}\). Potenciál libovolného bodu v tomto obvodu je roven napětí tohoto bodu vůči N. Tak například potenciál bodu P je \(\varphi_P=U_{PN}=6\ \mathrm{V}\). Body C a N jsou spojeny ideálním vodičem, a leží tudíž na stejné ekvipotenciální hladině, proto \(\varphi_C=\varphi_N=0\ \mathrm{V}\). Napětí \(U_{BC}=\varphi_B-\varphi_C=3{,}2\ \mathrm{V}\), takže \(\varphi_B=3{,}2\ \mathrm{V}\). Zatímco napětí měříme vždy mezi dvěma body a je určeno jednoznačně, potenciál se vztahuje pouze k určitému bodu obvodu a jeho hodnota závisí na tom, kde jsme si zvolili referenční bod.
Otázka pro šikovné: Proč musí být v diskutovaném obvodu zapojen rezistor a jaký je jeho odpor?

