Ohyb – pozorování
Při studiu mechanických vlnění jsme si všimli, že se vlny ohýbají, když například prochází otvorem v překážce, jehož rozměry jsou srovnatelné s vlnovou délkou.


Zdroj
Světlo se za podobných podmínek chová naprosto stejně. Již jsme se s tímto jevem seznámili v kapitole 2. při měření tloušťky lidského vlasu.
Zdroj
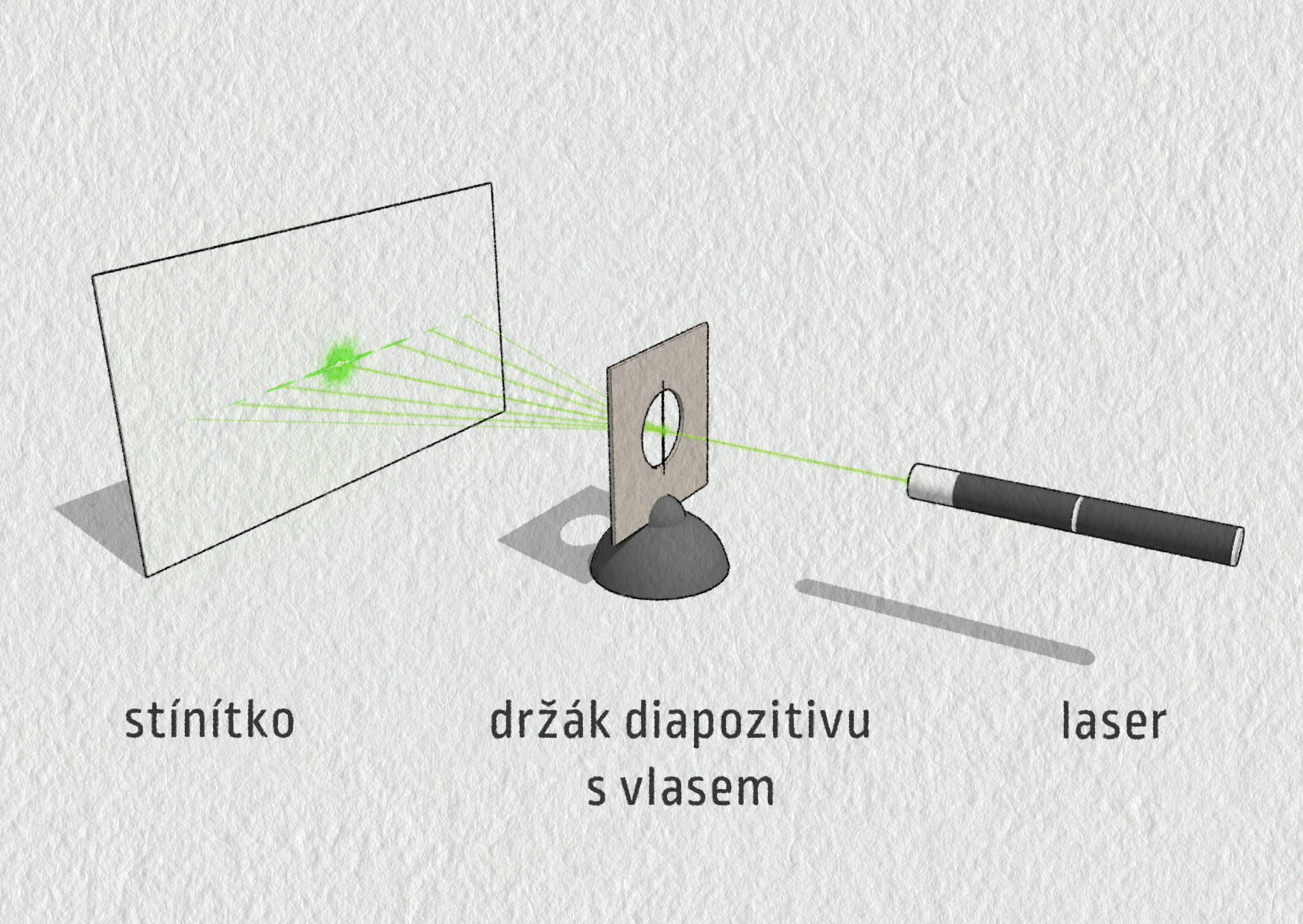
Laserový paprsek dopadající na tenký drát nebo úzkou štěrbinu se vlivem difrakce rozšíří, ohýbá se.
Difrakce/ohyb
Ohyb světla je deformace světelných vln překážkou. Světlo se tak může dostat i do míst geometrického stínu za překážkou.
Ohyb světla

Zdroj

Zdroj

Zdroj

Zdroj
Ohyb na štěrbině – vlastnosti
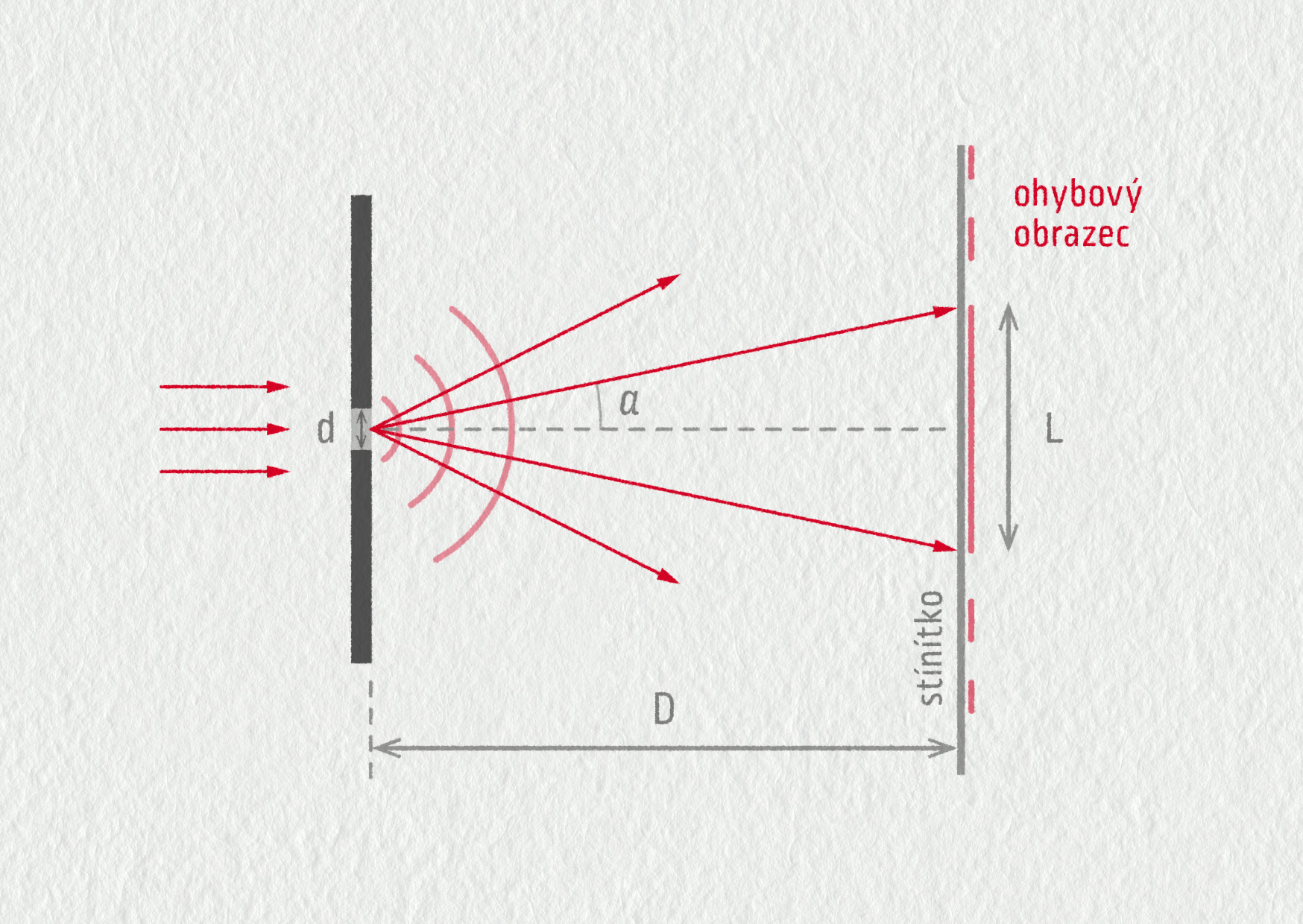
Uvažujme nyní světelnou vlnu, která dopadá na úzký podlouhlý otvor – štěrbinu, jejíž šířku označíme \(d\). Vlna se ohýbá do stran, rozšiřuje se. Na stínítku ve vzdálenosti \(D\) od štěrbiny pozorujeme ohybový obrazec, v němž je výrazné centrální maximum šířky \(L\). Čím je štěrbina užší (\(d\) je menší), tím je ohyb výraznější (\(L\) je větší). Kvůli ohybu světla tak není experimentálně možné vytvořit libovolně úzký světelný paprsek.
Zdroj
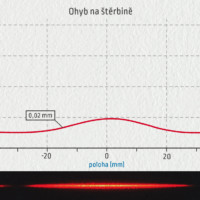
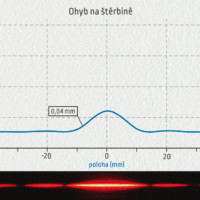
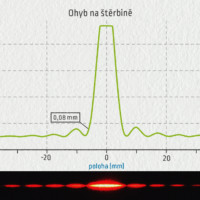
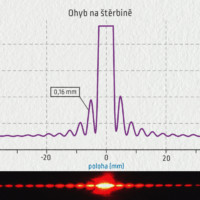
Prohlédněte si grafy naměřené pro čtyři různě široké štěrbiny.
Zdroj
Zdroj
Zdroj
Zdroj
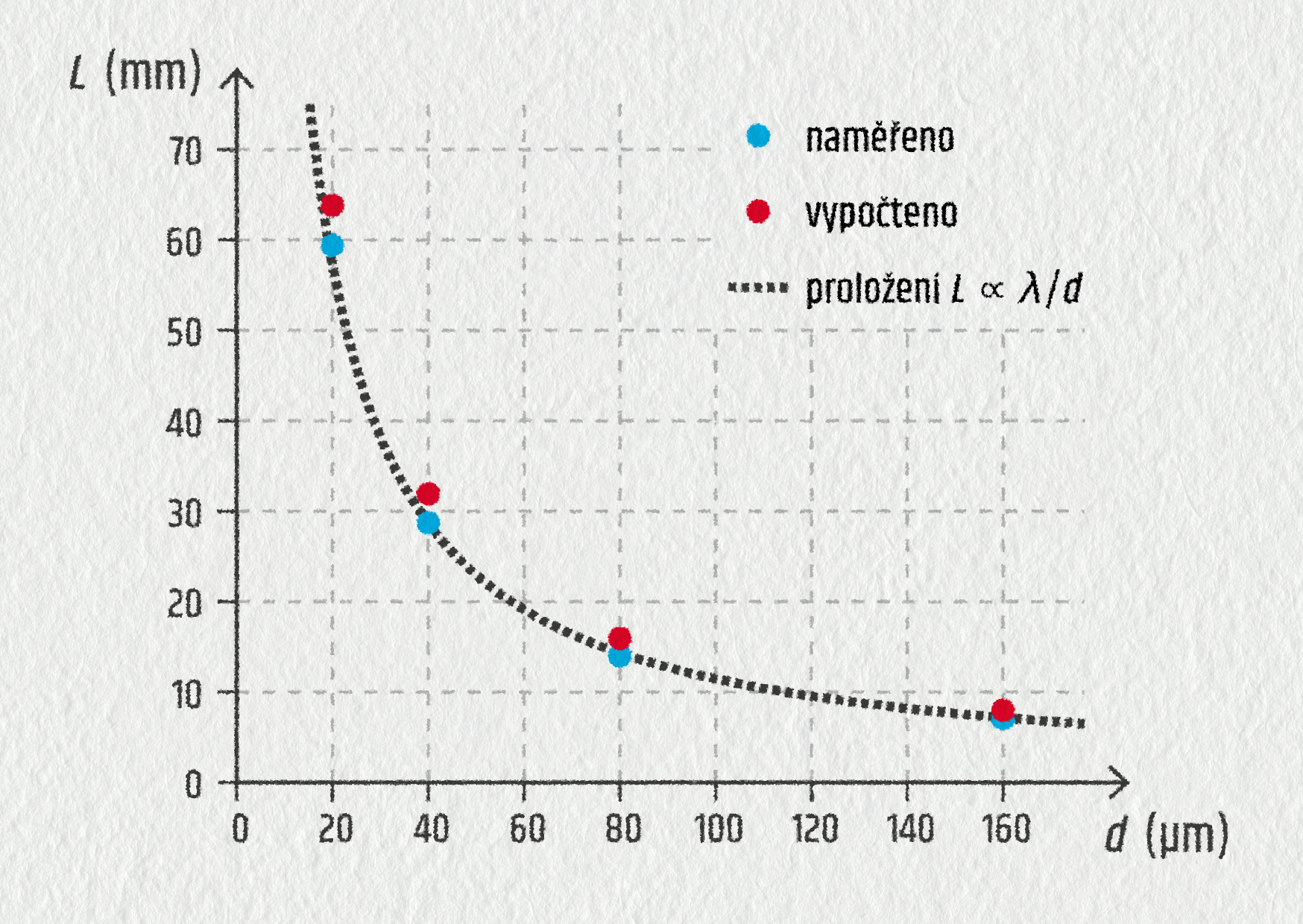
Výsledky měření lze také zpracovat do jednoduchého grafu, který ukazuje, že při ohybu na štěrbině je šířka centrálního maxima \(L\) nepřímo úměrná šířce štěrbiny \(d\) (matematicky zapsáno \(L\propto\lambda/d\)). Pokud bychom použili světlo o vyšší vlnové délce \(\lambda\), bude se šířka \(L\) opět zvětšovat.
Zdroj
Ze schématu experimentu (obrázek 24.26) můžeme vidět, že polovina centrálního maxima o velikosti \(L/2\) je vidět na vzdálenost \(D\) pod úhlem \(\theta\). Protože vzdálenost \(D\gg l\), úhel \(\theta\) je velmi malý, a můžeme tedy psát
\[ \theta\approx\tan\theta=\frac{L/2}D=\frac{L}{2D} \](viz matematické dodatky). Vzhledem k úměře \(\theta\propto\lambda/d\) lze také psát \(L/2D=\lambda/d\). Jestliže tedy ohybový obrazec pozorujeme na stínítku ve vzdálenosti \(D\) od štěrbiny, pak pro šířku centrálního ohybového maxima nalezneme vztah \(L=2\lambda D/d\).
Kdy vlastně můžeme ohyb na štěrbině pozorovat? Platí nějaká podmínka pro vlnovou délku světla a šířku štěrbiny?
Podívejme se na předchozí vztah podívat čistě matematicky. Uvažujme štěrbinu, jejíž šířka je celistvý násobek vlnové délky světla: \(d=k\lambda\). Vychýlení světelné vlny z jejího původního směru je tedy
\[ \theta = \frac{\lambda}d = \frac{\lambda}{k\lambda} = \frac1k\;. \]Jestliže vezmeme štěrbinu, jejíž šířka je 100krát větší než vlnová délka světla (\(d=100\lambda\)), dostaneme úhel
\[ \theta = \frac1k = \frac1{100} = 10^{-2}\ \mathrm{rad} = 0{,}57^\circ\;. \]Tento úhel způsobí na stínítku vzdáleném 3,0 m centrální maximum široké 3,0 cm. Ohyb tedy můžeme pozorovat.
V případě, že vezmeme štěrbinu užší (\(d=10\lambda\)), bude mít úhel \(\theta\) velikost 5,7°. Ohyb je tedy 10krát výraznější. Jestliže máme naopak štěrbinu o šířce \(d=1000\lambda\), bude mít úhel \(\theta\) velikost 0,06°, a ohyb tak nebude téměř pozorovatelný.
Vidíme tedy, že ohybové jevy pro světlo nejsou pozorovatelné, jestliže je rozměr štěrbiny o několik řádů větší než vlnová délka světla.
Neméně zajímavý výsledek dostaneme při ohybu světla na kruhovém otvoru průměru \(d\). První minimum (tmavý kroužek) tentokrát najdeme pod úhlem \(\theta\) splňujícím podmínku \(\theta=1{,}22\lambda/d\) (pro malé úhly). Tato podmínka nám umožní podívat se blíže na rozlišení optických přístrojů.
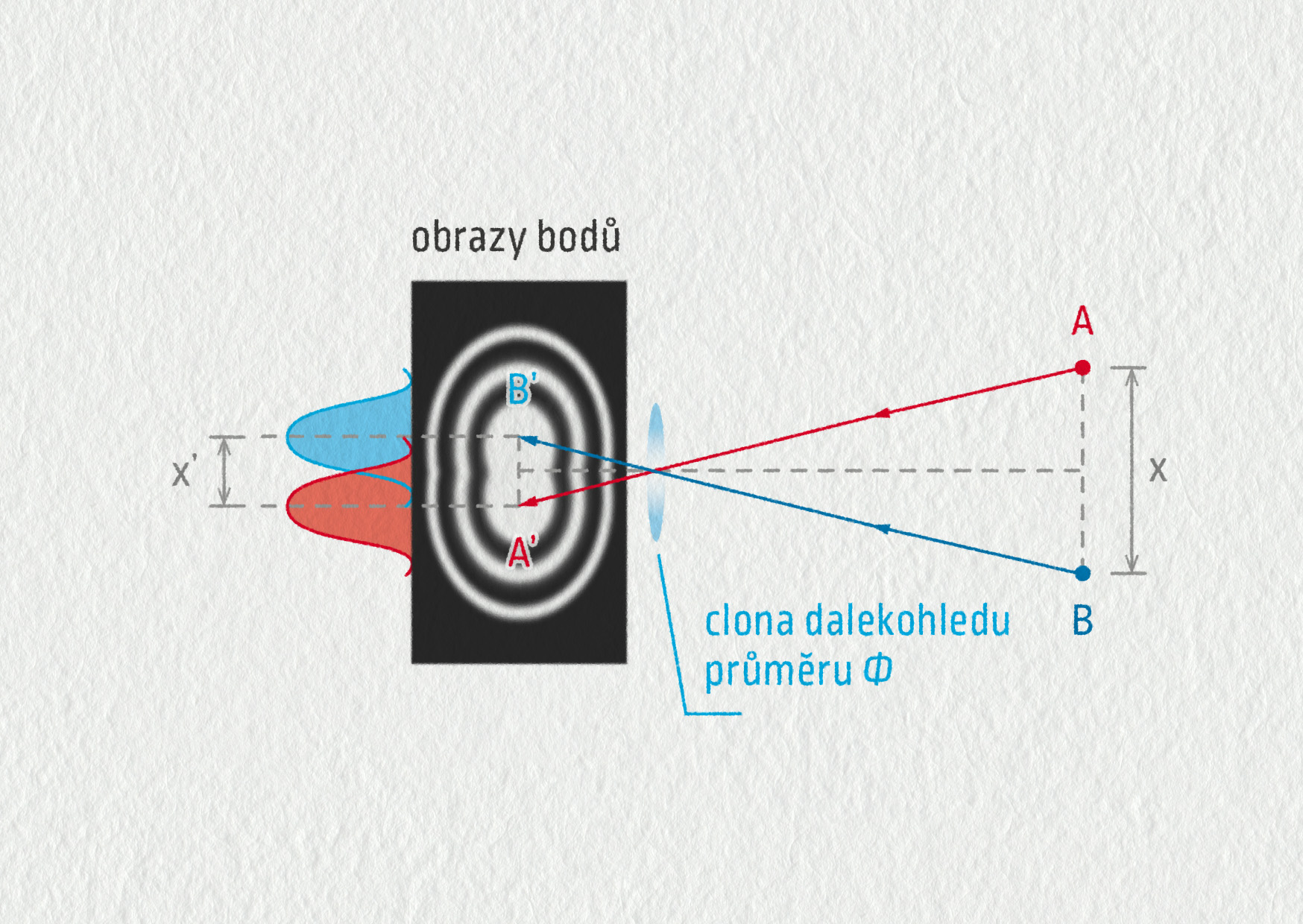
Ohyb světla má rozhodující vliv na to, jakým způsobem vidíme svět. Kruhové čočky dalekohledů a mikroskopů, zrcadla dalekohledů, stejně tak i lidské oko působí jako clona o průměru \(\Phi\), skrze kterou prochází světlo. Clona světlo ohýbá stejně jako štěrbina nebo kruhový otvor (viz Galerie – Ohyb světla).
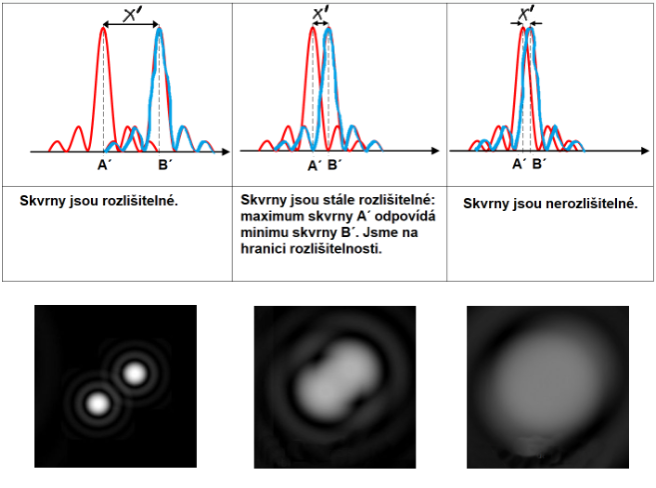
Obraz bodu tak není bodem, ale kruhovou skvrnou, kolem které jsou ještě soustředné prstence. Pozorujeme-li tedy dva body A a B, optický přístroj nám zobrazí dva body A′ a B′, které mají tvar difrakčních skvrn.
Zdroj
Zdroj
Obrazy A′ a B′dvou bodů jsou rozlišitelné, jestliže jejich vzdálenost \(x'=|A'B'|\) je větší než poloměr centrálních disků v ohybových skvrnách. Jinými slovy minimum ohybového obrazce jednoho bodu musí odpovídat maximu ohybového obrazce druhého bodu.
Pro úhel \(\theta\) tedy platí \(\theta>1{,}22\lambda/\Phi\), kde \(\Phi\) značí průměr objektivu přístroje.
Čím je průměr objektivu přístroje \(\Phi\) větší, tím menší detaily na obrazu dokážeme rozlišit. I to je jeden z důvodů, proč stavíme stále větší dalekohledy.
Jaký nejmenší předmět dokážeme na povrchu Měsíce rozlišit dalekohledem, který má průměr objektivu 5 m? (Vzdálenost Země–Měsíc činí 384 000 km, jako vlnovou délku světla zvolíme přibližně střed viditelné oblasti, tedy 580 nm.)
Vyjdeme z podmínky pro úhel \(\theta\), pod kterým vidíme daný předmět na povrchu Měsíce (viz obrázek). Úhel \(\theta\) je velmi malý, platí tedy
\[ \frac xD = \theta = 1{,}22\frac{\lambda}{\Phi}\;. \]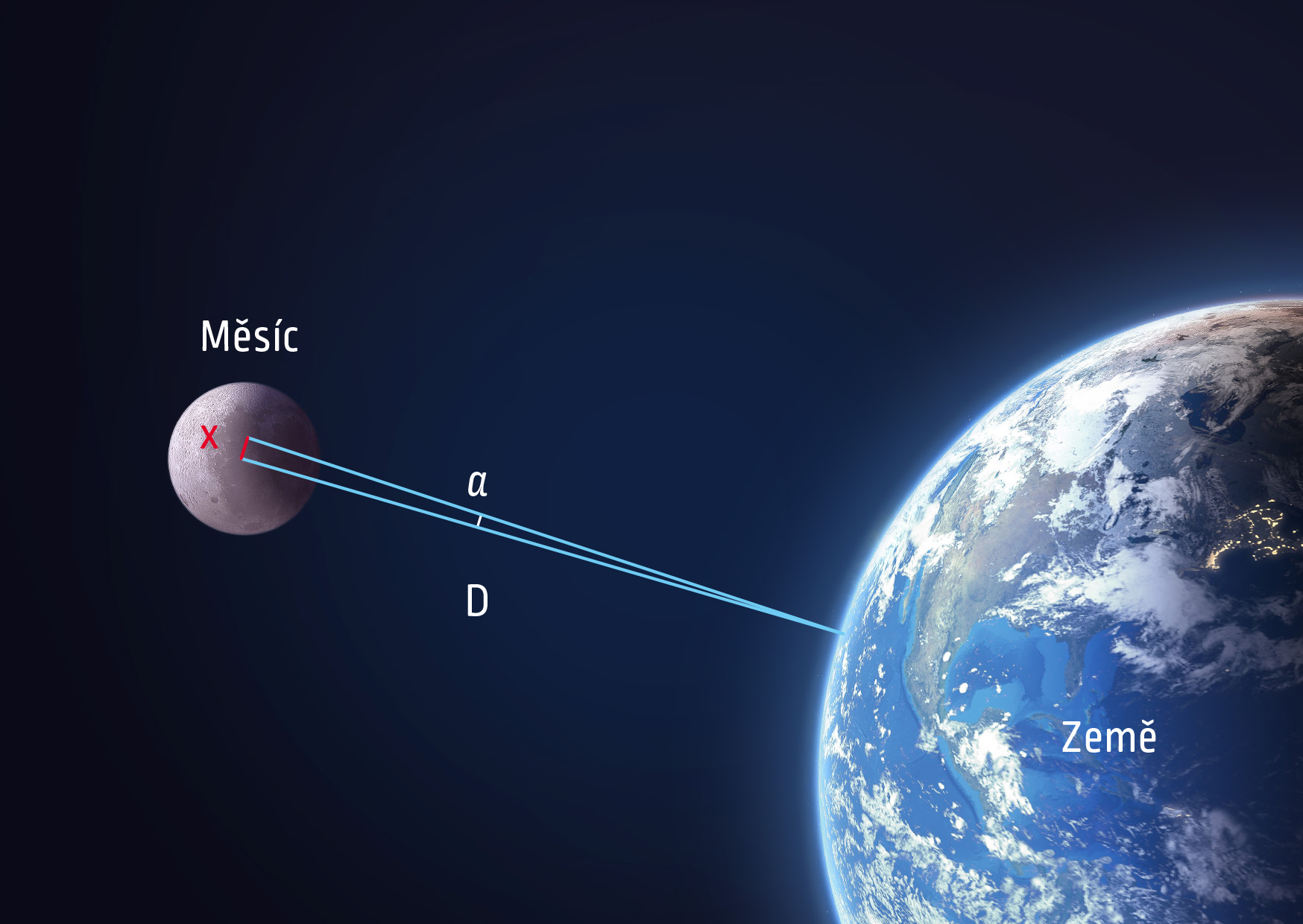
Zdroj
Odtud pak vyjádříme vztah pro velikost detailu na povrchu Měsíce: \(x=D\cdot1{,}22\lambda/\Phi\). Číselným dosazením vypočítáme
\[ x = 384\cdot10^6\cdot1{,}22\cdot\frac{5{,}80\cdot10^{-7}}{5}\ \mathrm{m} = 54\ \mathrm{m}\;. \]Jakmile ovšem dosáhneme úhlového rozlišení oka nebo čipu CCD, který zachytává světlo, zvětšovat průměr dalekohledu již nemá smysl. Technická konstrukce detektoru světla také omezuje rozlišovací schopnost přístroje.

