Interference na dvojštěrbině
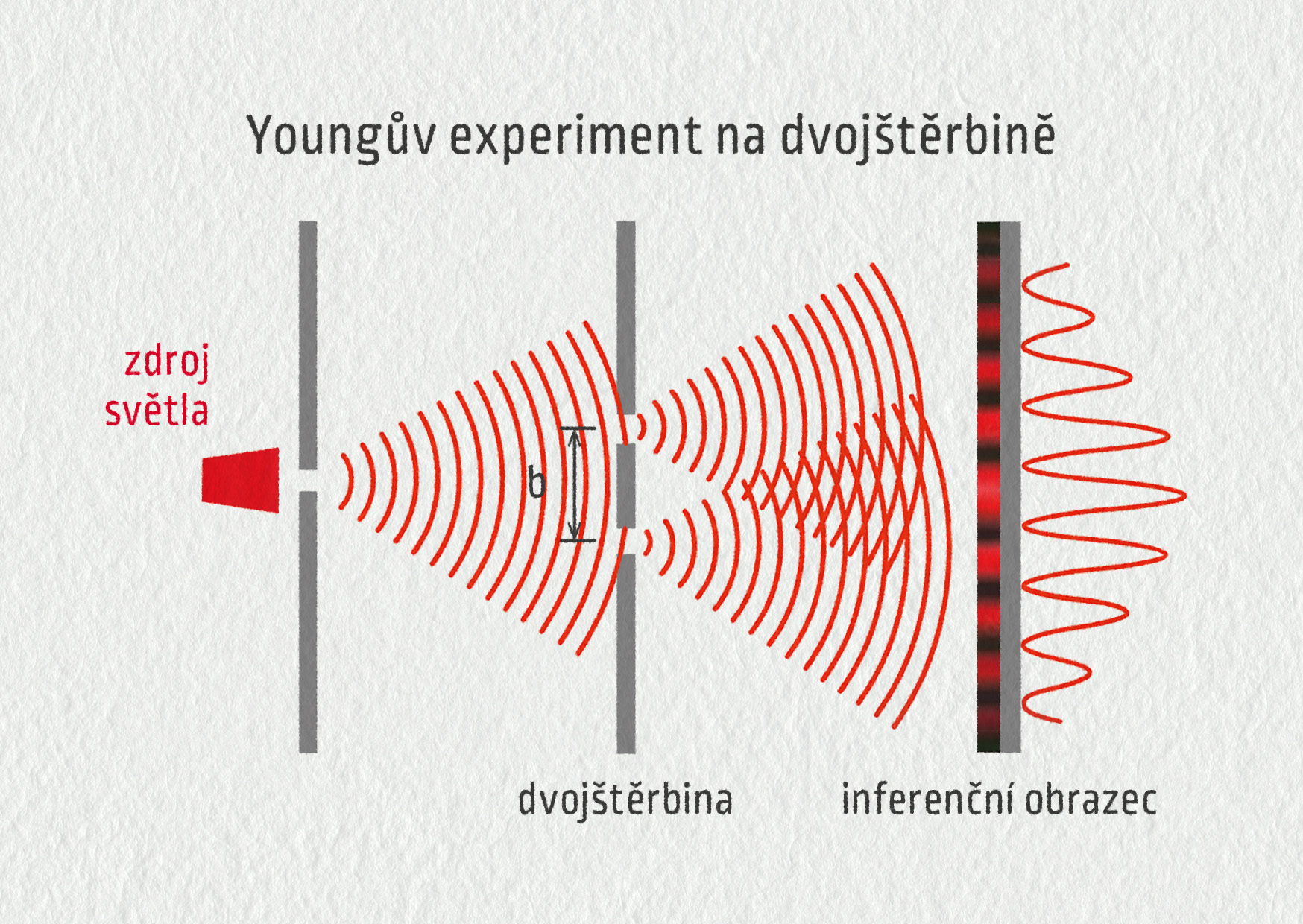
Dalším důkazem vlnové povahy světla je jeho interference. Dobře ji popisuje slavný Youngův pokus s dvojštěrbinou (viz schéma). Přestože Thomas Young prováděl svůj experiment s bílým slunečním světlem (viz video), v našem výkladu budeme pro jednoduchost předpokládat pouze monochromatické světlo.
Zdroj
V tomto experimentu nechal Thomas Young dopadat světelné vlnění z jednoho úzkého zdroje na dvě totožné úzké štěrbiny, které byly od sebe ve vzdálenosti \(b\). Dnes bychom jako zdroj použili laser. Vlnění vycházející ze štěrbin se spolu překrývala a v místě, kde docházelo k překrytí, Young pozoroval jejich skládání. Na stínítku vzniklo množství světlých a tmavých světelných čar – interferenční obrazec.

Zdroj
Interference světelných vlnění
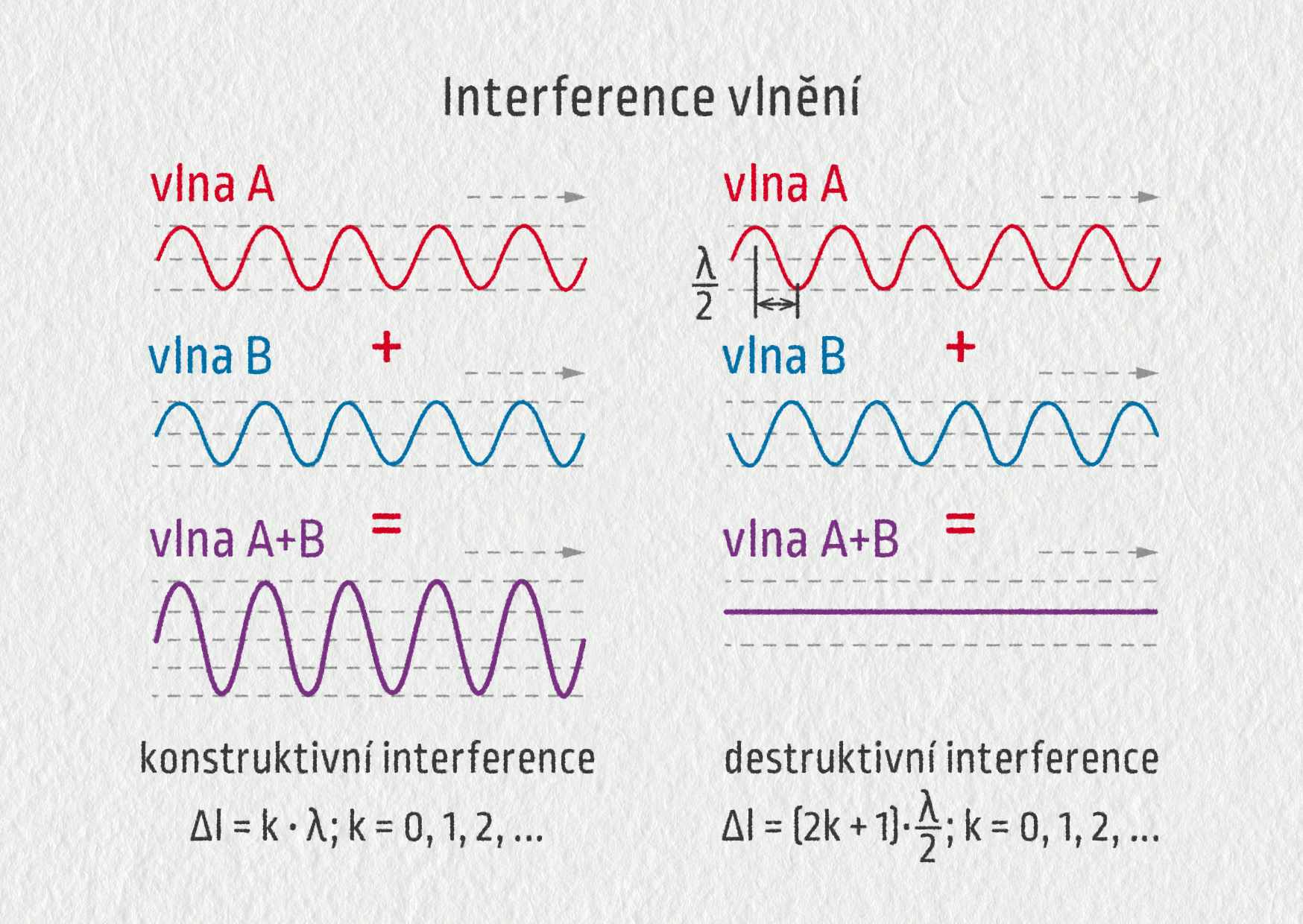
Interference světelných vlnění je jejich vzájemné skládání. Výsledkem může být jak světlý proužek (konstruktivní interference), tak tmavý proužek (destruktivní interference).
Štěrbiny se chovají jako dva téměř bodové zdroje světla o téže frekvenci (a téže vlnové délce). Oba tyto zdroje osvětlují plochu stínítka, kde pozorujeme jejich skládání.
Pokud do určitého bodu na stínítku dopadnou tyto vlny ve fázi (obě vlny nabývají současně v určitý okamžik maxima a v jiný okamžik minima), složí se spolu konstruktivně a vytvoří vlnění o vyšší amplitudě (viz obrázek 24.34). V takovém bodě vznikne na stínítku světlý proužek.
Pokud do jiného bodu na stínítku dopadnou světelné vlny s opačnou fází (v daný okamžik má jedna vlna maximum a současně druhá vlna minimum), jejich složením vzniká vlnění s menší, nebo dokonce nulovou amplitudou. Pak hovoříme o destruktivní interferenci. V tomto případě pozorujeme na stínítku tmavý proužek. Přestože je daný bod osvětlen oběma zdroji, složením dvou světel může vzniknout tma. Jde o jasný důkaz vlnového charakteru světla.
Zdroj
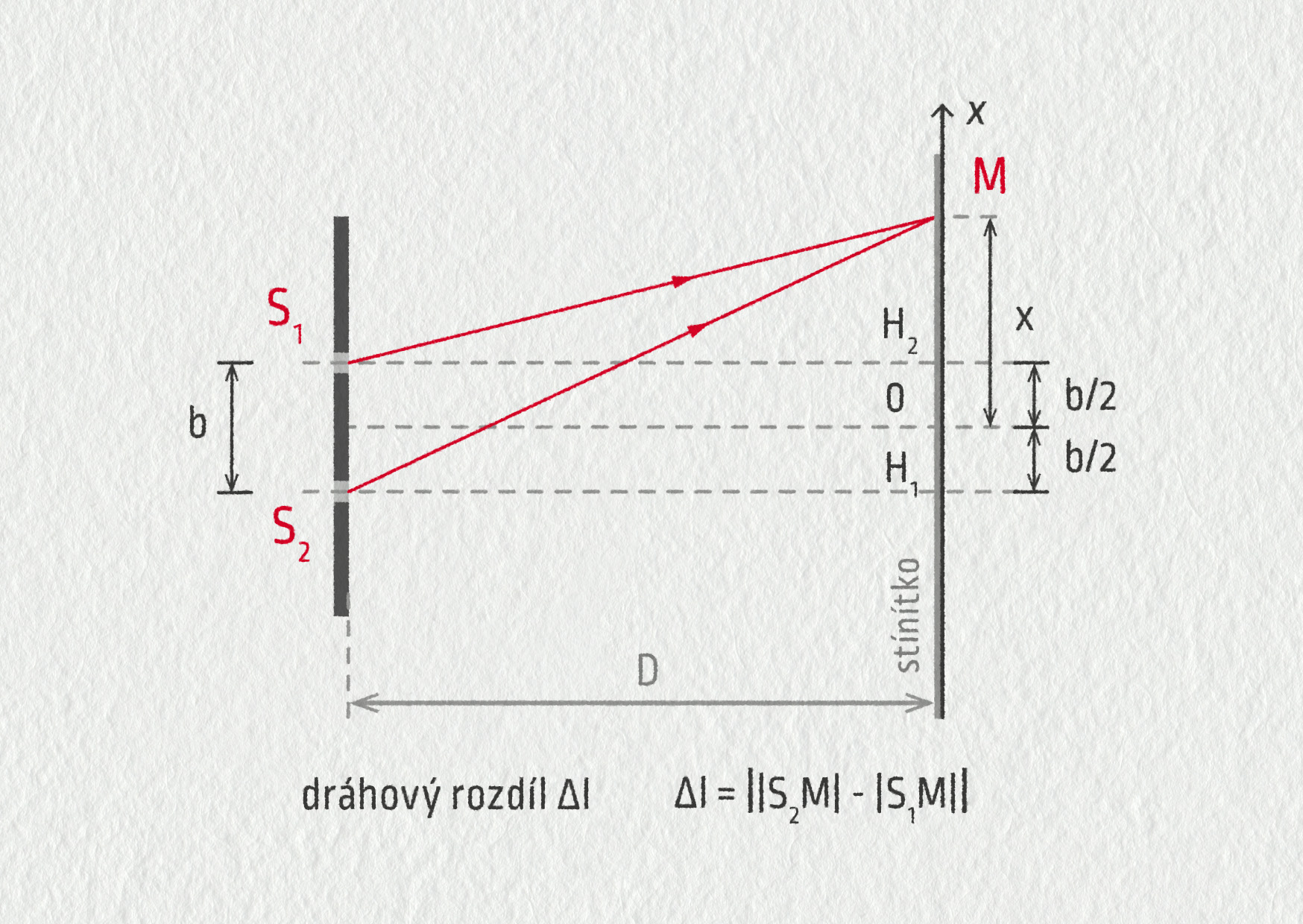
Podívejme se na Youngův experiment, jehož uspořádání je znázorněno na obrázku 24.35.
Zdroj
Dráhový rozdíl \(\Delta l=\bigl||S_2M|-|S_1M|\bigr|\) vyjadřuje rozdíl mezi vzdálenostmi, které urazí vlny šířící se z bodu S1 a S2 a interferující v bodě M na stínítku. Poloha bodu M je dána vzdáleností \(x\) od středu stínítka.
Na vzdáleném stínítku vzniká interferenční obrazec (obrázek 24.36) s množstvím střídajících se světlých a tmavých proužků, to znamená střídajících se interferenčních maxim a minim. Tato minima, stejně jako maxima, jsou na stínítku pravidelně rozmístěna.

Zdroj
Uprostřed stínítka (bod O) najdeme světlý proužek – interferenční maximum. To je bod, který je stejně daleko od obou štěrbin a obě vlnění do něj dorazila se stejnou fází, neboť na své cestě urazila stejnou dráhu. Došlo ke konstruktivní interferenci, dráhový rozdíl je \(\Delta l=0\) (\(k=0\)). Nalezli jsme centrální maximum.
Posuneme-li se na stínítku o malý kousek stranou (bod M), vlnění z jedné štěrbiny muselo urazit o kousek delší dráhu. Je-li dráhový rozdíl \(\Delta l=\lambda/2\), vlnění jsou v opačné fázi a na stínítku se objeví první tmavý proužek – interferenční minimum. Posuneme-li se ještě o kousek dále, znovu se ocitneme v místě s interferenčním maximem. Tentokrát je však dráhový rozdíl mezi oběma vlnami roven \(\Delta l=1\lambda\). Vlnění jsou opět ve fázi, dostáváme první postranní maximum (\(k=1\) pak označuje řád tohoto maxima).
Podobně můžeme vysvětlit i vznik dalších postranních maxim a minim.
Vztah pro interferenci na dvojštěrbině
Na stínítku tedy vidíme pravidelně se střídající minima a maxima, světlé a tmavé body nebo proužky. Pro jejich polohy platí následující vztah:
Určení polohy interferenčního maxima
\[ b\sin\theta = k\lambda \]\(b\) ... vzdálenost štěrbin
\(\lambda\) ... vlnová délka světla
\(\theta\) ... úhel, pod kterým vidíme polohu \(k\)-tého maxima z pozice štěrbiny
Tento vztah můžeme také vyjádřit pomocí \(xb/D=k\lambda\), kde jsme použili vztah \(\sin\theta\simeq\tan\theta=x/D\), který platí pro malé úhly \(\theta\), což je zde splněno.
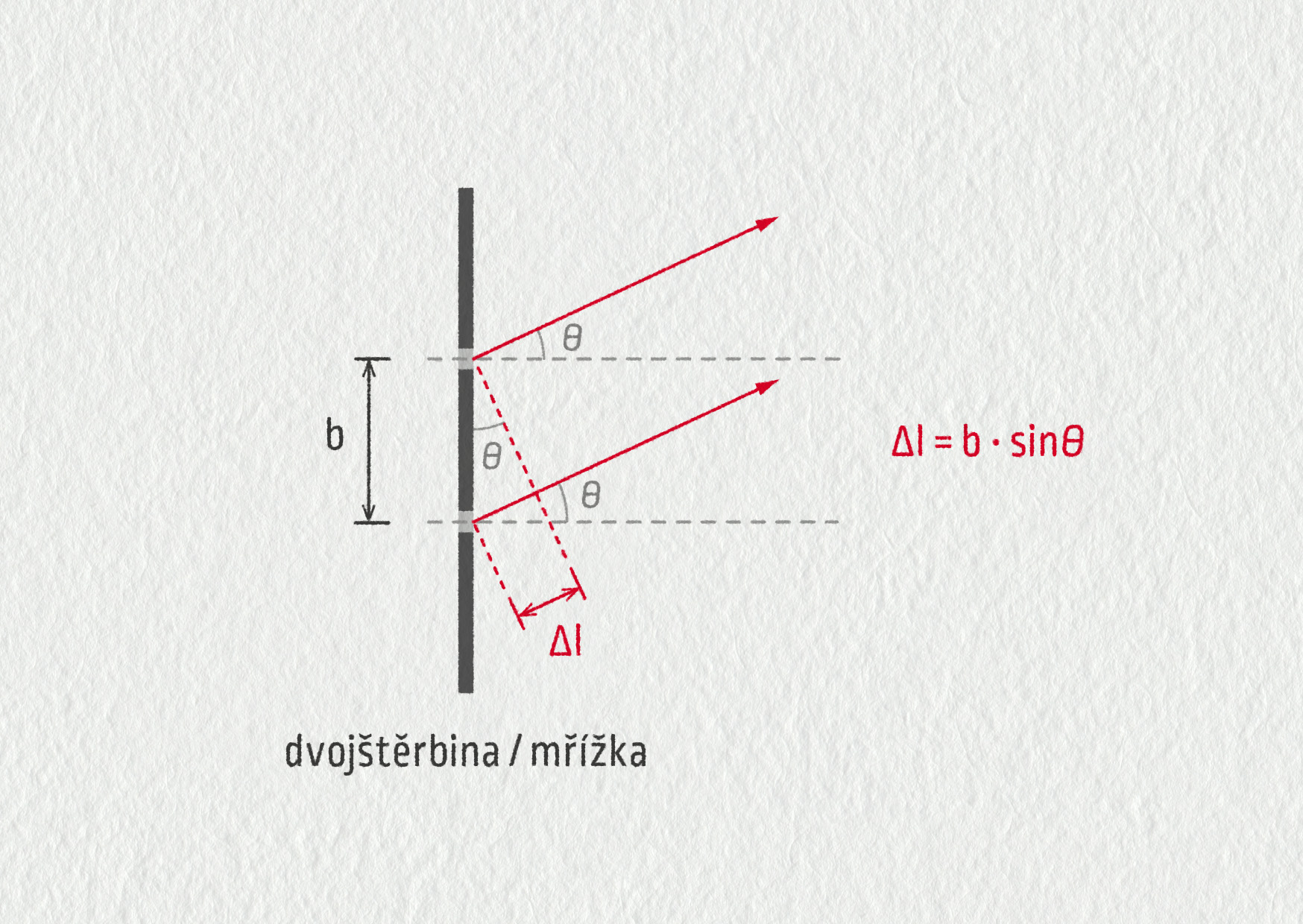
Podívejme se, jak tento vztah matematicky odvodit. Budeme předpokládat, že světelné vlnění dopadá na dvě rovnoběžné štěrbiny, které jsou od sebe vzdáleny \(b\). (Poznamenejme, že tento vztah platí také pro interferenci na mřížce – viz dále v této kapitole –, neboť tvar interferenčního obrazce je zcela stejný jako v případě dvojštěrbiny, pouze získáme jasnější obraz, protože mřížkou prochází více světla.) Matematická podmínka pro konstruktivní interferenci na dvojštěrbině platí tedy naprosto stejně i pro mřížku se stejnou vzdáleností štěrbin.
Zdroj
Jestliže uvažujeme velmi vzdálené stínítko, na kterém vzniká interferenční obrazec, jsou skládající se vlny prakticky rovnoběžné. Jejich dráhový rozdíl pak můžeme vyjádřit velmi jednoduše z pravoúhlého trojúhelníku jako \(\Delta l=b\sin\theta\), kde \(b\) je vzdálenost sousedních štěrbin a \(\theta\) úhel, pod kterým vidíme bod M z pozice mřížky.
V případě konstruktivní interference je dráhový rozdíl \(\Delta l=k\lambda\), a proto dostáváme hledaný vztah \(b\sin\theta=k\lambda\).
V Youngově experimentu osvěcujeme dvojštěrbinu monochromatickým zdrojem o vlnové délce \(\lambda=600\ \mathrm{nm}\). Uvažujme bod M na stínítku, který je od jedné štěrbiny vzdálen \(d_1\) a od druhé \(d_2\). Nastane v bodě M konstruktivní, nebo destruktivní interference, jestliže
- \(d_2-d_1=0\),
- \(d_2-d_1=3\ \mu\mathrm{m}\),
- \(d_2-d_1=4{,}5\ \mu\mathrm{m}\)?
Ke konstruktivní interferenci dojde, jestliže je dráhový rozdíl
\[ \Delta l=d_2-d_1=k\lambda=2k\frac{\lambda}2 \]neboli dráhový rozdíl je roven sudému násobku poloviny vlnové délky. Vypočítejme tedy podíl
\[ N = \frac{d_2-d_1}{\displaystyle\frac{\lambda}2} = \frac{2(d_2-d_1)}{\lambda}\;. \]Pokud bude tento podíl roven sudému číslu, nastane v bodě M konstruktivní interference, pokud lichému, nastane v bodě M destruktivní interference.
- Při nulovém rozdílu se nacházíme ve středu stínítka, kde je světlý proužek neboli konstruktivní interference.
- \(N=(3\cdot2)/0{,}6=10\), v tomto bodě je tedy interferenční maximum.
- \(N=(4{,}5\cdot2)/0{,}6=15\), v tomto bodě je tedy interferenční minimum.
Červené světlo o vlnové délce 752 nm prochází skrze dvojštěrbinu, jejíž štěrbiny jsou od sebe vzdáleny 6,20 ⋅ 10−5 m. Dvojštěrbina je ve vzdálenosti 2,20 m od stínítka.
- Pod jakým úhlem se odklání světelné vlnění odpovídající prvnímu světlému proužku na stínítku? V jaké vzdálenosti od středu stínítka toto maximum leží?
- Pod jakým úhlem se odklání světelné vlnění odpovídající druhému tmavému proužku na stínítku? V jaké vzdálenosti od středu stínítka toto maximum leží?
- Jak se změní poloha prvního centrálního maxima, jestliže v experimentu použijeme zelené světlo o vlnové délce 520 nm?
a) První maximum odpovídá \(k=1\). Interferenční podmínku pro maximum píšeme ve tvaru \(b\sin\theta_\mathrm{a}=k\lambda\). Pro velikost úhlu tedy platí:
\[ \theta_\mathrm{a} = \mathop{\mathrm{arcsin}}\frac{k\lambda}b\;. \]Číselným dosazením získáváme \(\theta_\mathrm{a}=0{,}695^\circ\). Poloha tohoto maxima na stínítku může být určena pomocí vztahu \(\tan\theta_\mathrm{a}=y_\mathrm{a}/D\), který vychází z pravoúhlého trojúhelníku (viz obrázek).
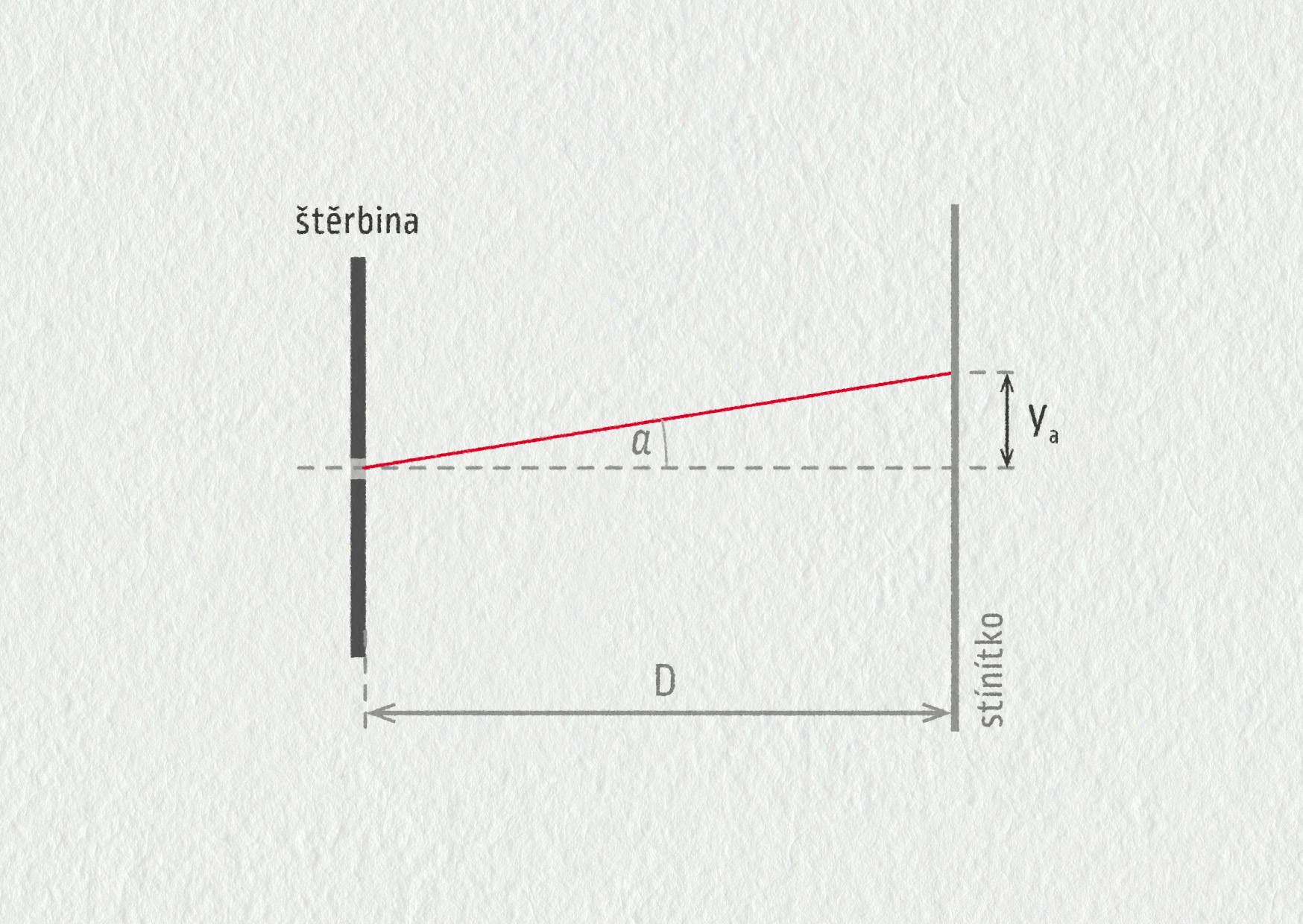
Zdroj
Pro polohu maxima na stínítku tak získáváme \(y_\mathrm{a}=D\tan\theta_\mathrm{a}=2{,}20\tan(0{,}695^\circ)=0{,}027\ \mathrm{m}\).
b) Druhý tmavý proužek (minimum) odpovídá také \(k=1\). Interferenční podmínku pro minimum píšeme ve tvaru
\[ b\sin\theta_\mathrm{b}=(2k+1)\frac{\lambda}2 \;. \]Pro velikost úhlu tedy platí:
\[ \theta_\mathrm{b} = \mathop{\mathrm{arcsin}}\frac{\displaystyle(2k+1)\frac{\lambda}2}b\;. \]Číselným dosazením získáváme \(\theta_\mathrm{b}=1{,}04^\circ\).
Podobně jako v předchozí části obdržíme \(y_\mathrm{b}=D\tan\theta_\mathrm{b}=2{,}20\tan(1{,}04^\circ)=0{,}040\ \mathrm{m}\).
c) Protože vlnová délka zeleného světla je menší než vlnová délka červeného světla, bude i poloha minima nebo maxima pro zelené světlo v kratší vzdálenosti než pro červené světlo. Vypočítejme znovu část a), tentokrát ale pro zelené světlo:
\[ y_\mathrm{az}=\frac{\lambda_\mathrm{z}D}d=\frac{5{,}20\cdot10^{-7}\cdot2{,}20}{6{,}2\cdot10^{-5}}=0{,}018\ \mathrm{m}\; \]Interference na mřížce
Optická mřížka je vlastně větší množství štěrbin, které jsme srovnali rovnoběžně vedle sebe. Obvykle ji charakterizujeme počtem štěrbin \(N\) na 1 mm nebo mřížkovou konstantou \(b=1/N\), která vyjadřuje, jak daleko jsou od sebe sousední štěrbiny. Mřížkovou konstantu také nazýváme perioda mřížky.

Zdroj
Jestliže mřížku osvěcujeme laserovým svazkem, jednotlivé štěrbiny se chovají přibližně jako bodové zdroje světla a na stínítku se skládá interferenční obrazec. Ten je tvořen sérií jasných maxim (světelných bodů odpovídajících hlavním maximům) a poměrně širokých tmavých pásů, kde bychom nalezli pravidelně se opakující velmi slabá sekundární maxima. Hlavní maxima jsou od sebe vzdálena tím více, čím je menší perioda mřížky. Při kolmém dopadu světla na mřížku platí pro konstruktivní interferenci na mřížce stejný vztah jako pro interferenci na dvojštěrbině \(b\sin\theta=k\lambda\). Jestliže má mřížka hodně štěrbin (mřížková konstanta \(b\) je menší), jsou hlavní maxima velmi úzká, sekundární maxima pak lze zcela zanedbat.
Ze zmíněného vztahu vidíme, že odchýlení světla od původního směru (úhel \(\theta\)) je větší, jestliže použijeme světlo s vyšší vlnovou délkou \(\lambda\). Proto se v interferenčním obrazci na mřížce maxima stejného řádu pro zelené světlo nacházejí ve větší vzájemné vzdálenosti než pro modré světlo (viz obrázek).

Zdroj
Pokud optickou mřížku osvítíme bílým světlem, pak mřížka rozloží světlo stejně jako optický hranol. Tohoto jevu využíváme při analýze světla v mnoha vědních oborech. Většina současných spektroskopů je vybavena kvalitními optickými mřížkami, které mají několik tisíc vrypů na 1 mm.

Zdroj
Více o spektroskopii a jejím využití se dozvíte v kapitole 25.
Jaká je mřížková konstanta mřížky, která vytvoří ve světle o vlnové délce 450 nm maximum prvního řádu pod úhlem 15°? Kolik má tato mřížka vrypů na 1 mm?
Pro mřížku platí vztah \(b\sin\theta=k\lambda\), musíme z něj tedy vyjádřit mřížkovou konstantu \(b\) vztahem
\[ b = \frac{k\lambda}{\sin\theta} = \frac{1\cdot4{,}50\cdot10^{-7}}{\sin(15^\circ)} = 1{,}7\cdot10^{-6}\ \mathrm{m}\;. \]To odpovídá počtu vrypů
\[ N = \frac1b = \frac1{1{,}7\cdot10^{-6}} = 588\,235\ \mathrm{m}^{-1}=588\ \mathrm{mm}^{-1}\;. \]Interference světla na tenké vrstvě
Při dopadu světla na tenkou vrstvu oleje na hladině vody nebo na mýdlové bublině vznikají zajímavé barevné skvrny. Co je způsobuje a jak můžeme jejich vznik vysvětlit?

Zdroj

Zdroj

Zdroj
Příčinou vzniku barev v těchto situacích, jak již víme, je konstruktivní a destruktivní interference na tenké vrstvě v odraženém světle. Jak k tomu dochází, se můžete podívat na následujícím schématu znázorňujícím vznik červené barvy v odraženém světle na mýdlové bublině.
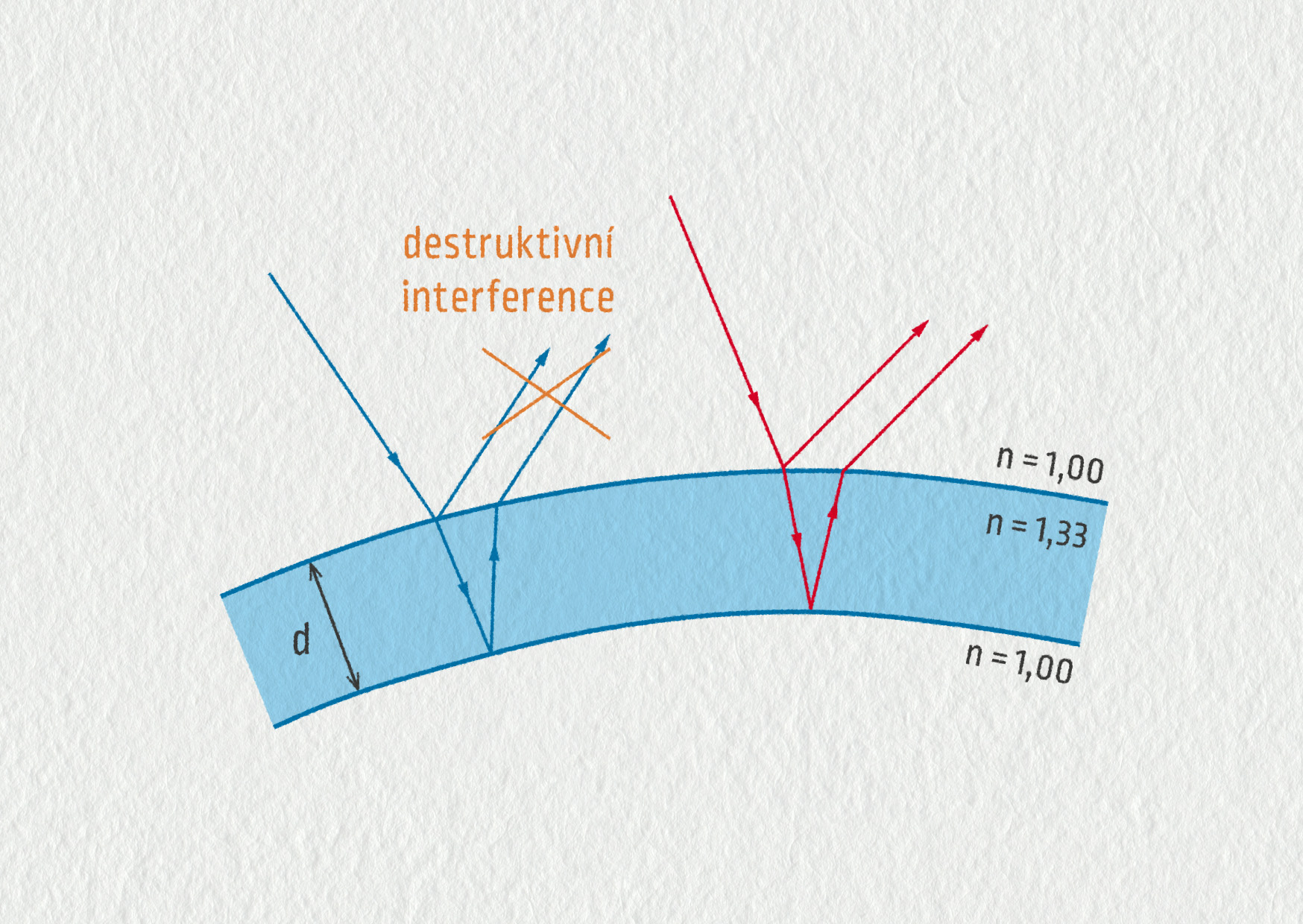
Zdroj
Abychom takovou interferenci dokázali alespoň přibližně popsat, podívejme se, co se děje při kolmém dopadu světla na tenkou vrstvu. Podaří se nám stanovit podmínku pro konstruktivní interferenci odražených vln 1′) a 2′)?
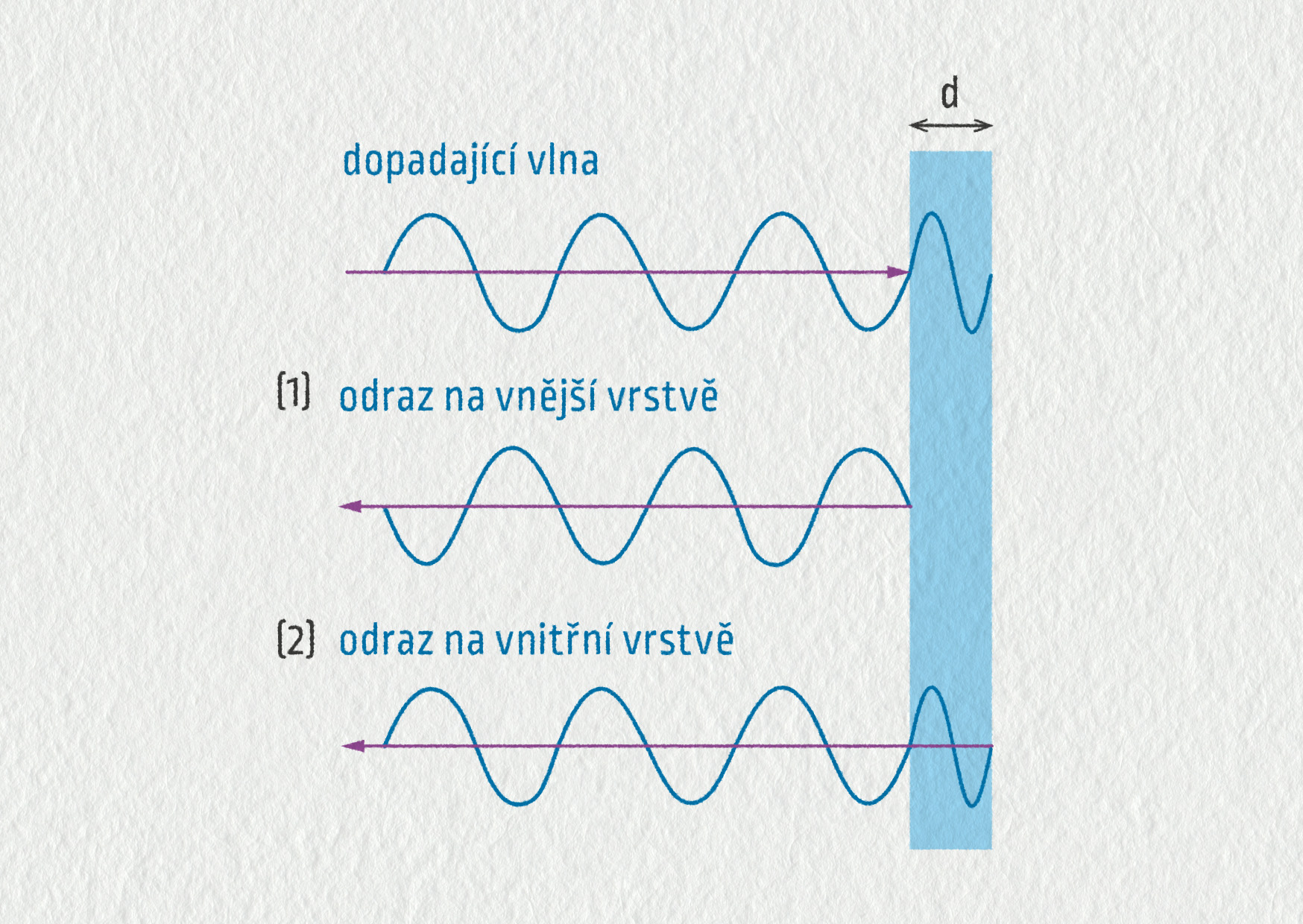
Zdroj
Dopadající světelná vlna se odráží na rozhraní vzduch–kapalina. Protože je kapalina opticky hustší než vzduch (index lomu \(n\)), dochází zde k otočení fáze (stejně jako při odrazu vlnění na pevném konci lana). Část světelné vlny pak pokračuje v kapalině, odráží se až na rozhraní kapalina–vzduch (zde již bez otočení fáze) a vrací se zpět jako vlna (2).
Jaký je dráhový rozdíl mezi vlnami (1) a (2)? Zatímco vlna (1) se šířila vzduchem, vlna (2) urazila v kapalině vzdálenost \(2d\) (\(d\) je tloušťka vrstvy). Protože se však v kapalině šíří \(n\)-krát menší rychlostí, vlna (1) mezitím ve vzduchu urazila \(n\)-krát větší vzdálenost, tedy \(2nd\). Navíc se jí otočila fáze, tudíž dráhový rozdíl \(\Delta l\) mezi odraženými vlnami (1) a (2) je možné vyjádřit jako
\[ \Delta l = 2nd + \frac{\lambda}2\;. \]Podmínka pro konstruktivní interferenci na tenké vrstvě je tedy
\[ 2k\frac{\lambda}2 = 2nd + \frac{\lambda}2\;. \]V odraženém světle proto uvidíme právě tu barvu, která splňuje předchozí podmínku. Ostatní barvy budou kvůli interferenci vln potlačeny. Protože se tloušťka vrstvy mění, můžeme na bublině pozorovat mnoho barevných proužků či skvrn. Jejich barva vždy odpovídá určité tloušťce vrstvy. Velmi pěkně je to vidět na svislé bublině, která kvůli gravitaci mění směrem dolů svou tloušťku.

Zdroj
S interferenčními jevy se setkáme i v přírodě. Struktura tělesných schránek některých brouků, křídel motýlů nebo minerálů je tak jemná a pravidelná, že tvoří optickou mřížku a barva je pak dána interferencí světla na této mřížce.
Interference v přírodě

Zdroj

Zdroj

Zdroj

Zdroj

Zdroj
Interferenci světla na tenké vrstvě také můžeme využít v technice. Optické prvky dalekohledů nebo třeba brýlí pokrýváme tenkou antireflexní vrstvou. Tato vrstva má za úkol eliminovat vznik parazitních odlesků na přední i zadní ploše čočky, přičemž využívá tzv. destruktivní interferenci. Dosahuje se toho pomocí nanesení tenké vrstvy (obvykle kolem 500 nm) různých oxidů tak, aby byl minimalizován odraz pro určitou vlnovou délku. Vrstev může být i několik na sobě. Zejména u slunečních brýlových čoček je důležité, aby byla antireflexní vrstva nanesena na zadní ploše čočky a do oka se nedostávaly paprsky odražené od vnitřní strany brýlí. Takové paprsky by komplikovaly vidění.
Využití antireflexní vrstvy

Zdroj

Zdroj

Zdroj

