Všechny elektrické jevy jsou důsledkem existence elektrického náboje. Náboj je vlastností některých elementárních částic – proton nese kladný náboj, elektron náboj záporný. Částice neutron má náboj nulový. Odpovídající fyzikální veličina elektrický náboj se značí písmenem \(q\), pokud jde o částice, nebo \(Q\), pokud jde o nabitá makroskopická tělesa. Jednotkou elektrického náboje je coulomb C.
Náboj protonu je nejmenší nedělitelný náboj, nazýváme jej elementární náboj, značíme jej \(e\), jeho hodnota je \(q_\mathrm{p}=e=+1{,}602\cdot10^{-19}\ \mathrm{C}\). Náboj elektronu je pak \(q_\mathrm{e}=-e=-1{,}602\cdot10^{-19}\ \mathrm{C}\).
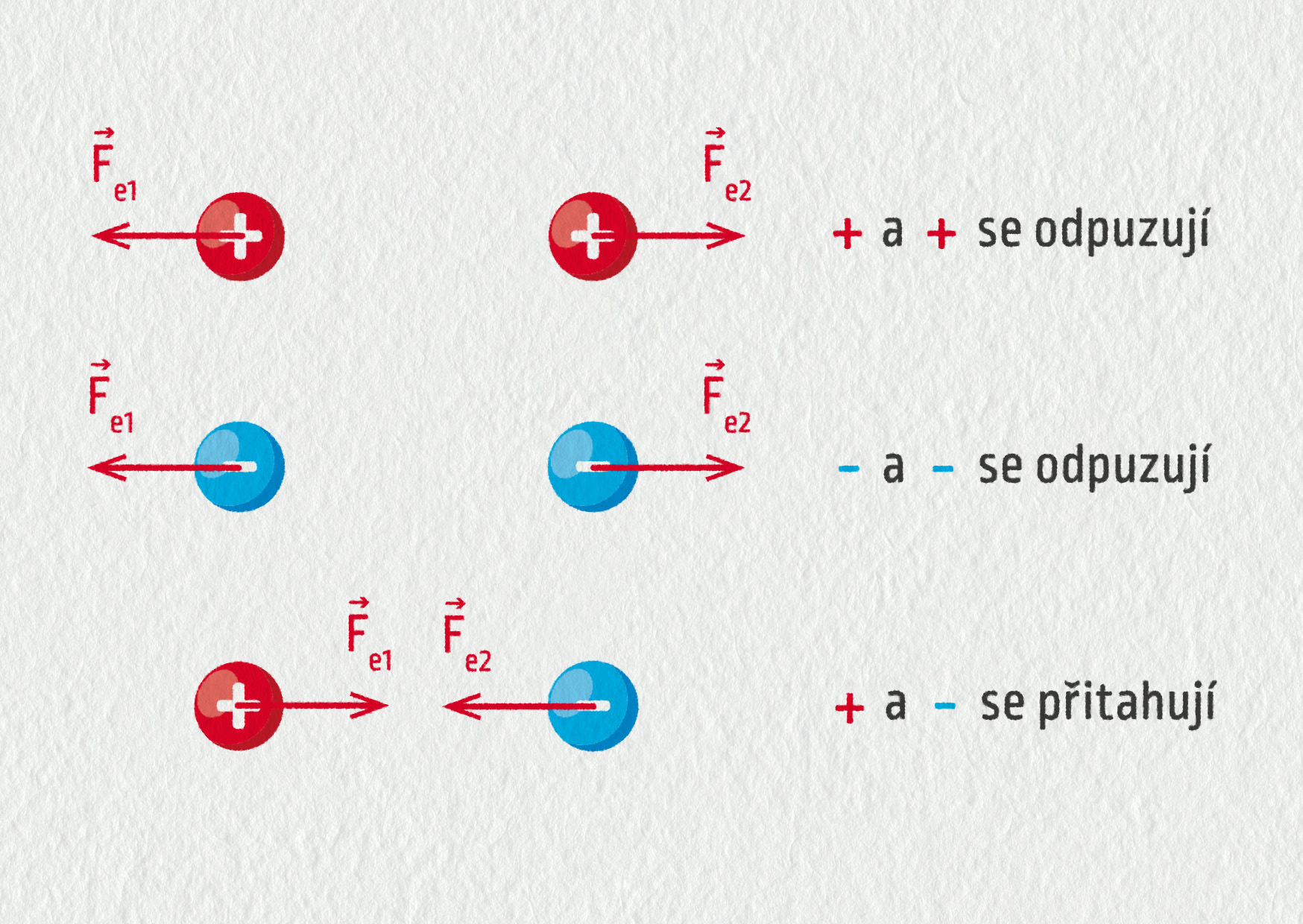
Náboje na sebe působí elektrickými silami: náboje stejného znaménka se odpuzují, náboje opačného znaménka se přitahují.
Zdroj
V této kapitole věnované elektrickému poli, pohybu nabitých částic, urychlovačům a výbojům v plynech budeme potřebovat základní znalosti o nábojích. Pokud byste v tuto chvíli váhali, jak určit například celkový náboj iontu \({}^6_3\mathrm{Li}^+\), vřele doporučujeme zopakovat první oddíl kapitoly Elektrické veličiny.
Coulombův zákon
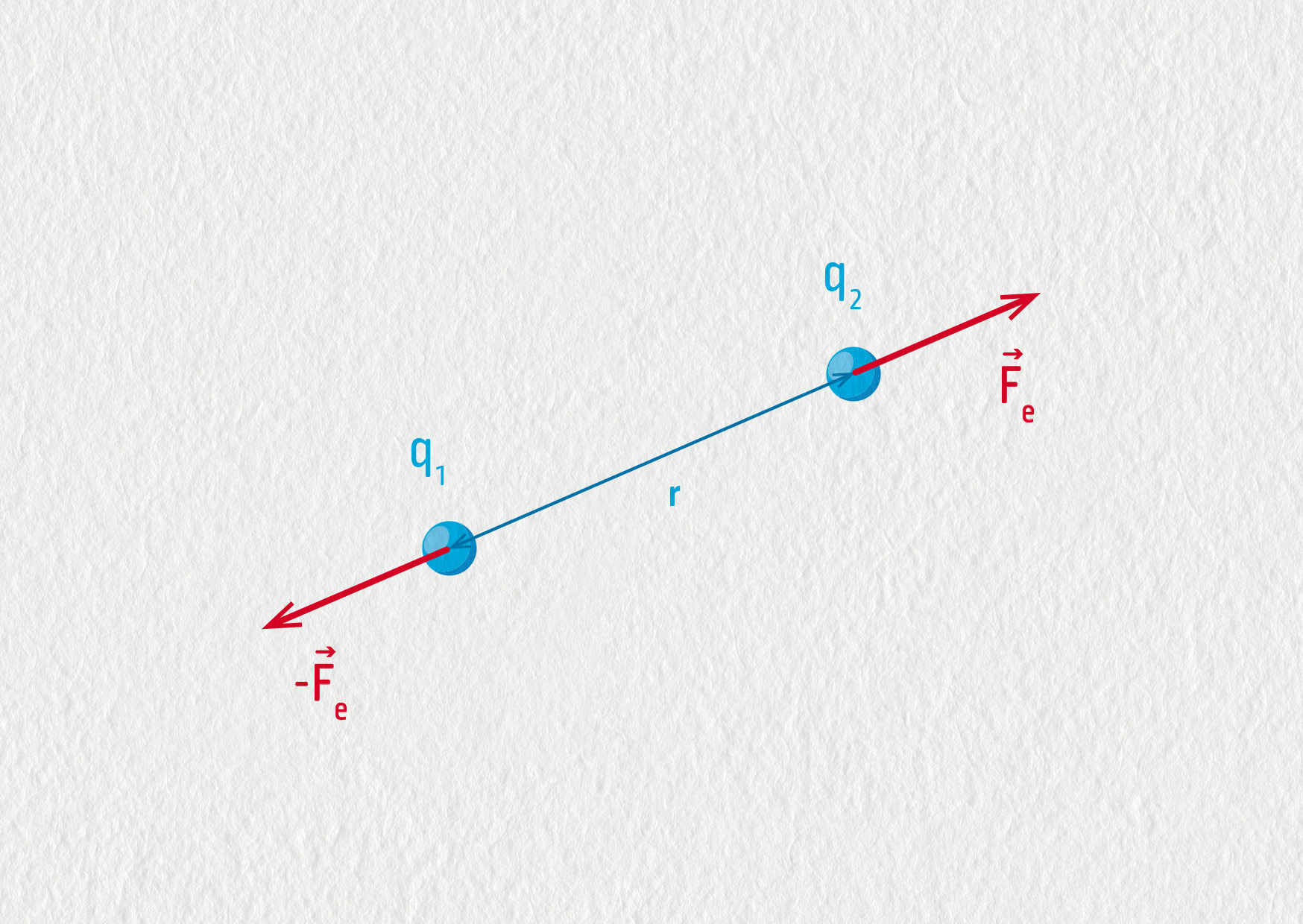
Uvažujme dvě částice nesoucí elektrický náboj \(q_1\) a \(q_2\). Předpokládejme, že částice jsou v klidu a jejich vzdálenost je \(r\). Elektrické síly, jimiž na sebe tyto částice působí, mají směr spojnice a orientaci podle znaménka nábojů („stejná znaménka = odpuzování“, „opačná znaménka = přitahování“). Velikost elektrické síly \(\Vec{F}_\mathrm{e}\) vypočítáme podle Coulombova zákona.
Zdroj
Coulombův zákon
\[F_\mathrm{e} = k\frac{|q_1q_2|}{r^2}\]\(F_\mathrm{e}\) ... elektrická síla v N
\(q_1\), \(q_2\) ... náboje částic v C
\(r\) ... vzdálenost nábojů v m
\(k\) ... konstanta
Ve vakuu a ve vzduchu \(k=9{,}0\cdot10^9\ \mathrm{N}\cdot\mathrm{m}^2\cdot\mathrm{C}^{-2}\)
Coulombův zákon říká, že elektrická síla je přímo úměrná součinu velikostí nábojů a nepřímo úměrná druhé mocnině jejich vzdálenosti. Ve vzorci pro \(F_\mathrm{e}\) musíme vzít absolutní hodnotu ze součinu nábojů, neboť velikost elektrické síly \(F_\mathrm{e}\) je vždy kladná hodnota.
Coulombův zákon v tomto tvaru platí také pro makroskopická tělesa s kulově symetrickým rozložením náboje a pro tělesa, jejichž rozměry jsou zanedbatelné vzhledem k jejich vzdálenosti.
Velikost elektrické síly je ovlivněna také prostředím, v němž se náboje nacházejí. Nejčastěji uvažujeme částice ve vakuu nebo nabitá tělesa ve vzduchu, ale mohou se vyskytovat i v jiném prostředí, např. být zalita v plastu. Tato závislost je skryta v konstantě, která se v současné fyzice vyjadřuje pomocí permitivity prostředí \(\varepsilon\)
\[ k = \frac1{4\pi\varepsilon}\;. \]Permitivita je veličina popisující elektrické vlastnosti prostředí, v němž se náboje nacházejí. Její jednotkou je farad na metr F ⋅ m−1. Permitivita vakua se značí \(\varepsilon_0\) a má hodnotu \(\varepsilon_0=8{,}854\cdot10^{-12}\ \mathrm{F}\cdot\mathrm{m}^{-1}\).
Působení mezi náboji je podle třetího Newtonova zákona vzájemné: působí-li náboj \(q_1\) na náboj \(q_2\) silou \(\Vec{F}_\mathrm{e}\), pak také náboj \(q_2\) působí na \(q_1\) elektrickou silou \(-\Vec{F}_\mathrm{e}\), která je stejně velká a opačně orientovaná.
Coulombův zákon je analogií Newtonova gravitačního zákona pro elektrické náboje v klidu. Podobně jako hmotnost je příčinou gravitace, je náboj příčinou elektrického působení. Gravitační síla je přímo úměrná součinu hmotností, elektrická síla přímo úměrná součinu nábojů. Obě síly jsou nepřímo úměrné druhé mocnině vzdálenosti.
Dvě malé kuličky umístěné ve vzduchu 30 cm od sebe nesou náboj 100 nC a –2 µC. Jak velkou silou se přitahují?
Zadané veličiny vyjádříme v základních jednotkách:
\(q_1=100\ \mathrm{nC}=10^{-7}\ \mathrm{C}\)
\(q_2=-2\ \mu\mathrm{C}=-2\cdot10^{-6}\ \mathrm{C}\)
\(r=30\ \mathrm{cm}=0{,}3\ \mathrm{m}\)
Ve vzduchu je \(k=9{,}0\cdot10^9\ \mathrm{N}\cdot\mathrm{m}^2\cdot\mathrm{C}^{-2}\).
Dosadíme do Coulombova zákona
\[F_\mathrm{e}=k\frac{|q_1q_2|}{r^2}=9\cdot10^9\cdot\frac{|10^{-7}\cdot(-2\cdot10^{-6})|}{0{,}3^2}\ \mathrm{N}=0{,}02\ \mathrm{N}\]Permitivity různých prostředí se v tabulkách nejčastěji uvádějí jakožto násobky permitivity vakua. Permitivitu hmotného prostředí tedy spočítáme jako \(\varepsilon=\varepsilon_0\varepsilon_\mathrm{r}\), kde \(\varepsilon_\mathrm{r}\) je tabelovaná relativní permitivita prostředí. Relativní permitivita číselně udává, kolikrát dané prostředí zeslabuje elektrickou sílu oproti vakuu.
| látka | \(\varepsilon_\mathrm{r}\) |
|---|---|
| vzduch | 1,00054 |
| papír | 3,5 |
| sklo | 3,8 až 19 |
| led | 4,8 |
| voda | 81 |
Poznamenejme, že permitivita prostředí ovlivňuje i rychlost šíření elektromagnetických vln. Dá se ukázat, že pro rychlost světla platí \(v=1/\sqrt{\varepsilon\mu}\), kde vedle elektrické permitivity \(\varepsilon\) vystupuje i magnetická permeabilita \(\mu\). Obě veličiny \(\varepsilon\) i \(\mu\) závisí na frekvenci vlnění.
Otázka pro šikovné: Dokázali byste vyjádřit jednotku farad (F) pomocí základních jednotek SI?
S elektrickou silou \(\Vec{F}_\mathrm{e}\) se počítá stejně jako s ostatními silami – můžeme porovnávat jejich velikosti, vektorově sčítat, dosazovat je do Newtonových zákonů. Pojďme si to ukázat na příkladech.
Porovnejte velikost elektrické a gravitační síly, kterou se přitahuje jádro a elektron v atomu vodíku. Hmotnosti částic jsou: hmotnost protonu \(m_\mathrm{p}=1{,}67\cdot10^{-27}\ \mathrm{kg}\), hmotnost elektronu \(m_\mathrm{e}=9{,}11\cdot10^{-31}\ \mathrm{kg}\).
Ještě než začneme počítat, tipněte si, která ze sil je větší a kolikrát.
Jádro atomu vodíku je tvořeno protonem. Mezi protonem a elektronem v obalu nejsou žádné jiné hmotné částice, nachází se tedy ve vakuu. Jejich vzdálenost označíme \(r\) – nebyla zadána, číselnou hodnotu nebudeme potřebovat.
Poměr velikostí elektrické a gravitační síly vyjádříme z Coulombova a gravitačního zákona
\[ \frac{F_\mathrm{e}}{F_\mathrm{g}} = \frac{\displaystyle k\frac{|q_1q_2|}{r^2}}{\displaystyle G\frac{m_pm_e}{r^2}} = \frac{k|q_1q_2|}{Gm_pm_e} =\] \[=\frac{9{,}0\cdot10^9\cdot|1{,}602\cdot10^{-19}(-1{,}602\cdot10^{-19})|}{6{,}67\cdot10^{-11}\cdot1{,}67\cdot10^{-27}\cdot9{,}11\cdot10^{-31}} =\] \[=2{,}3\cdot10^{39} \]Na úrovni atomů je tedy gravitační síla o 39 řádů slabší než síla elektrická. To znamená, že elektron je v obalu atomu vodíku vázán elektricky, gravitace je zanedbatelná. Přesto na úrovni planet, hvězd a galaxií převládá gravitace, neboť tyto vesmírné útvary jsou elektricky neutrální, a proto na sebe elektricky nepůsobí.
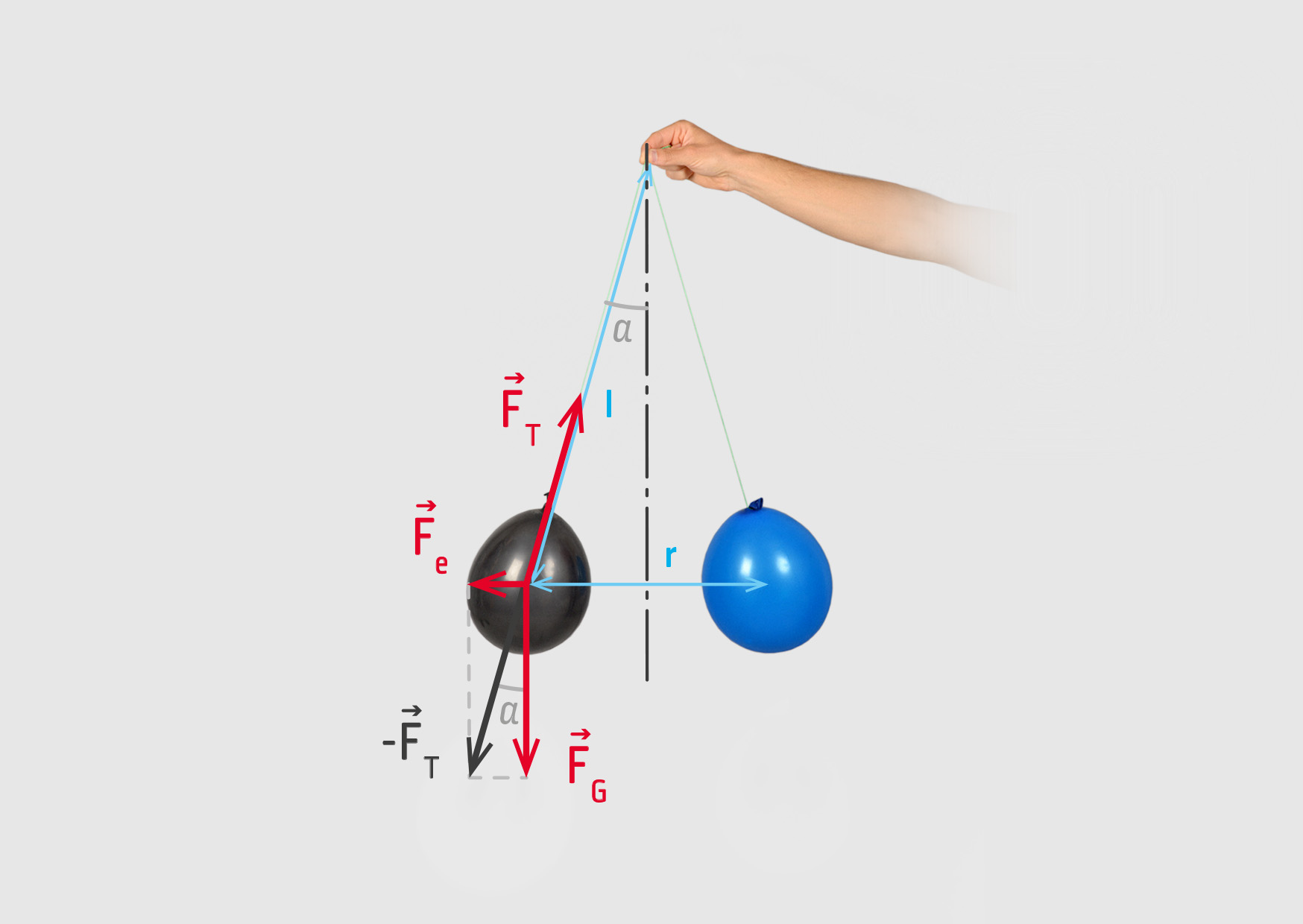
Dva pouťové balónky nafoukneme, přivážeme na tenkou nit a třením rovnoměrně zelektrujeme. Pro jednoduchost předpokládejme, že mají téměř kulový tvar, že jsou nabity stejně velkým nábojem \(q_1=q_2=q\) a že jejich hmotnost je stejná \(m_1=m_2=2{,}7\ \mathrm{g}\). Volný konec nití uchytíme v pevném bodě – viz obrázek 18.16. Vzdálenost těžiště balónku od bodu závěsu je 75 cm, nit svírá úhel 12° se svislým směrem. Jak velkým nábojem q jsou balónky nabity?

Zdroj
Ještě než začneme počítat, tipněte si, jak velký náboj balónky nesou 🙂
Řešení úlohy provedeme ve dvou krocích: nejdříve vypočítáme velikost elektrické síly \(F_\mathrm{e}\) a pak z Coulombova zákona určíme velikost nábojů \(q\).
Na černý balónek působí tři síly: tíhová síla \(\Vec{F}_\mathrm{G}\) svisle dolů, tahová síla \(\Vec{F}_\mathrm{T}\) ve směru provázku a elektrická síla \(\Vec{F}_\mathrm{e}\) vodorovně směrem doleva (stejné náboje se odpuzují) – viz obrázek 18.17.
Zdroj
Balónky setrvávají v klidu, takže podle prvního Newtonova zákona se působící síly musí vyrušit:
\[ \Vec{F}_\mathrm{G} + \Vec{F}_\mathrm{e} + \Vec{F}_\mathrm{T} = \Vec{0} \]To znamená, že současné působení \(\Vec{F}_\mathrm{G}\) a \(\Vec{F}_\mathrm{e}\) musí přesně kompenzovat tahová síla \(\Vec{F}_\mathrm{T}\):
\[ \Vec{F}_\mathrm{G} + \Vec{F}_\mathrm{e} = -\Vec{F}_\mathrm{T} \]Vektory \(\Vec{F}_\mathrm{G}\), \(\Vec{F}_\mathrm{e}\) a \(-\Vec{F}_\mathrm{T}\) tvoří pravoúhlý trojúhelník, v němž pro délky vektorů platí
\[ \tan\alpha=\frac{F_\mathrm{e}}{F_\mathrm{G}}\;. \]Velikost elektrické síly tedy spočítáme
\[ F_\mathrm{e} = F_\mathrm{G}\tan\alpha = mg\tan\alpha = 0{,}0027\ \mathrm{kg}\cdot9{,}81\ \mathrm{N/kg}\cdot\tan12^\circ = 0{,}0265\ \mathrm{N} = 26{,}5\ \mathrm{mN}\;. \]Známe-li elektrickou sílu, můžeme určit náboj \(q\). Z Coulombova zákona \(F_\mathrm{e}=kq^2/r^2\) vyjádříme neznámou
\[ |q| = r\sqrt{\frac{F_\mathrm{e}}k}\;, \]kde písmenem \(r\) jsme označili vzdálenost těžišť balónků. Vzdálenost \(r\) vypočítáme z pravoúhlého trojúhelníka – viz obrázek 18.17:
\[ \sin\alpha = \frac{r/2}l\;, \]takže
\[ r = 2l\sin\alpha = 2\cdot0{,}75\ \mathrm{m}\cdot\sin12^\circ = 0{,}312\ \mathrm{m} = 31{,}2\ \mathrm{cm}\;. \]Dosazením získáváme výsledek
\[ |q| = r\sqrt{\frac{F_\mathrm{e}}k} = 0{,}321\,\sqrt{\frac{0{,}0265}{9{,}0\cdot10^9}}\ \mathrm{C}=5{,}5\cdot10^{-7}\ \mathrm{C} = 550\ \mathrm{nC}\;. \]Balónky nesou náboj o velikosti 550 nC, buď jsou oba kladné, nebo oba záporné.
Tento výpočet vám může dát orientační představu, jak velký náboj mají běžná zelektrovaná tělesa – řádově stovky nanocoulombů. Jednotka 1 C tedy představuje obrovský náboj.

