Problémové úlohy

Cvičení 1

Vyšetření ultrazvukem

Problémová úloha – podle maturitního zadání z fyziky, Francie, 2005 (přeloženo a upraveno)

Dokument 1: Princip sonografie (podle C. Ray, J. C. Poizat – La physique par les objets quotidiens, Belin, 2007)

Sonda sonografu funguje současně jako vysílač i detektor ultrazvuku. Jakmile echo (odražená vlna) dopadne na sondu, vytvoří na převodníku malou změnu napětí. Pulzy trvají jen několik mikrosekund a opakují se po několika milisekundách, takže zvuková vlna má dost času vrátit se a být zaregistrována (zvuk v měkkých tkáních urazí přibližně 1,5 cm za 10 mikrosekund).

V závislosti na oblasti, kterou chceme zobrazit, se používají různé frekvence. Vlny o nízkých frekvencích se méně tlumí, takže prostředím pronikají hlouběji. Například při 5 MHz můžeme zkoumat oblasti až 12 cm hluboko, zatímco při 10 MHz dosáhneme jen 6 cm. Proč tedy nepoužívat vždy jen nízké frekvence? Protože na frekvenci závisí také přesnost měření, a to opačným způsobem, to znamená, že rozlišení je tím lepší, čím je frekvence vyšší (například při 5 MHz je rozlišení 0,3 mm a při 10 MHz až 0,15 mm).

Dokument 2: Schéma sonografického vyšetření mozku

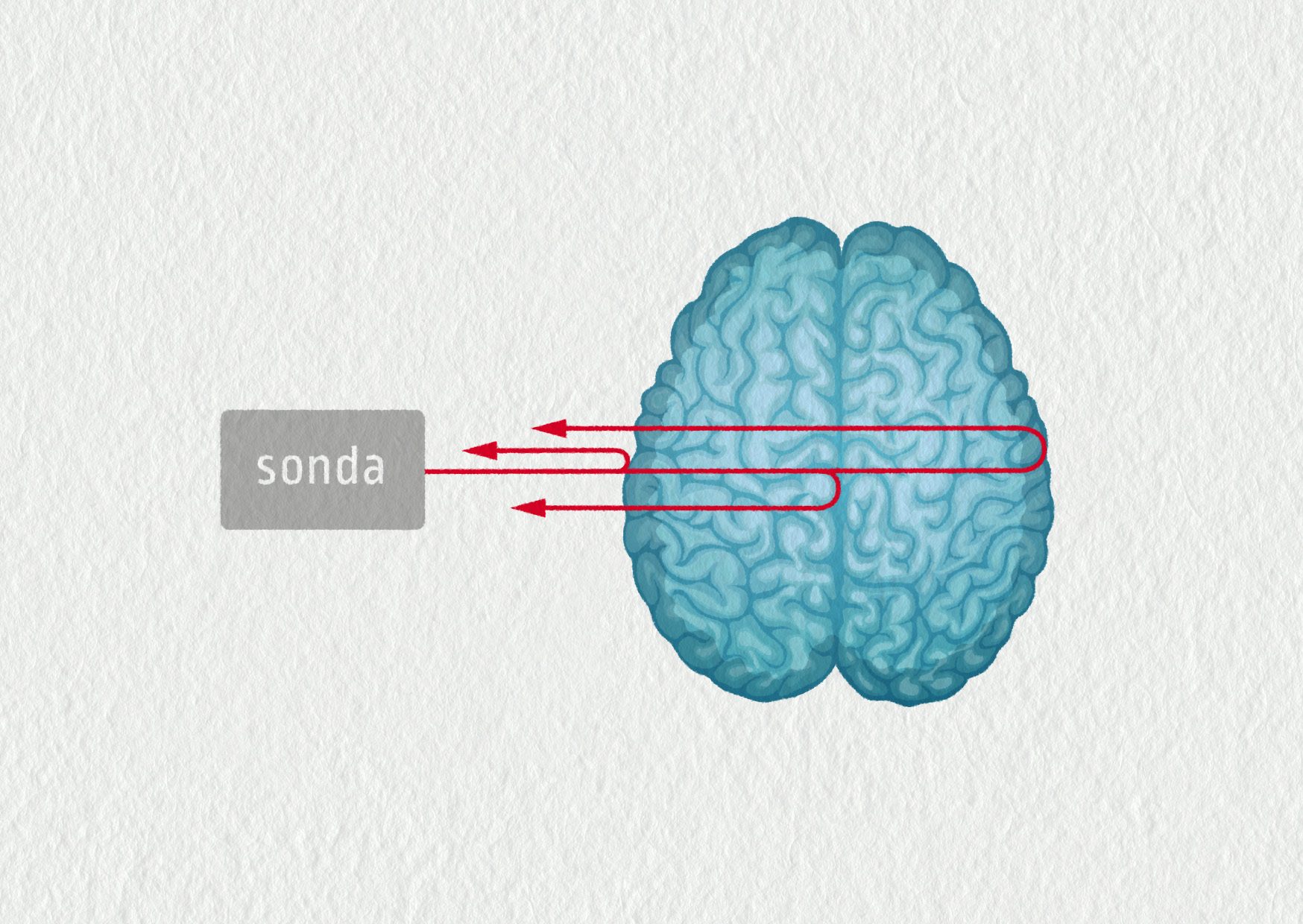
22.84 – Schéma sonografického vyšetření mozku.
Zdroj

Otázky:

Nakreslete časový průběh signálu vysílaného sondou a do grafu vyznačte časy charakteristické pro jednotlivé děje.
Jaká je rychlost ultrazvuku v měkkých tkáních?
Když se zvýší frekvence vlnění, jak se při tom změní
1. hloubka h zkoumané oblasti,
2. absolutní nejistota \(\Delta l\) měření délky?
Vypočítejte periodu a vlnovou délku pro frekvence 5,0 MHz a 10 MHz.
Jaký je vztah mezi vlnovou délkou a \(\Delta l / \lambda \)?
Jak se určí vzdálenost \(d\) okraje orgánu od sondy, když známe časový interval \(\Delta t\) mezi vysláním pulzu a jeho zachycením detektorem?
Použitelnost metody:
1. Do jaké největší vzdálenosti můžeme sonografem dohlédnout, jestliže interval \(\Delta t\) musí být menší než interval mezi dvěma pulzy?
2. Od jaké nejmenší vzdálenosti můžeme sonografem dohlédnout, jestliže interval \(\Delta t\) musí být delší než trvání jednoho pulzu?
Při vyšetření podle obrázku 22.84 zaregistrujeme tři odezvy: 10 µs, 160 µs a 310 µs po vyslání ultrazvukového pulzu. Jaká je šířka levé mozkové hemisféry?

22.85 – Snímek lidského plodu pořízený při ultrazvukovém vyšetření.
Zdroj

22.86 – Průběh signálu vysílaného sondou v závislosti na čase.
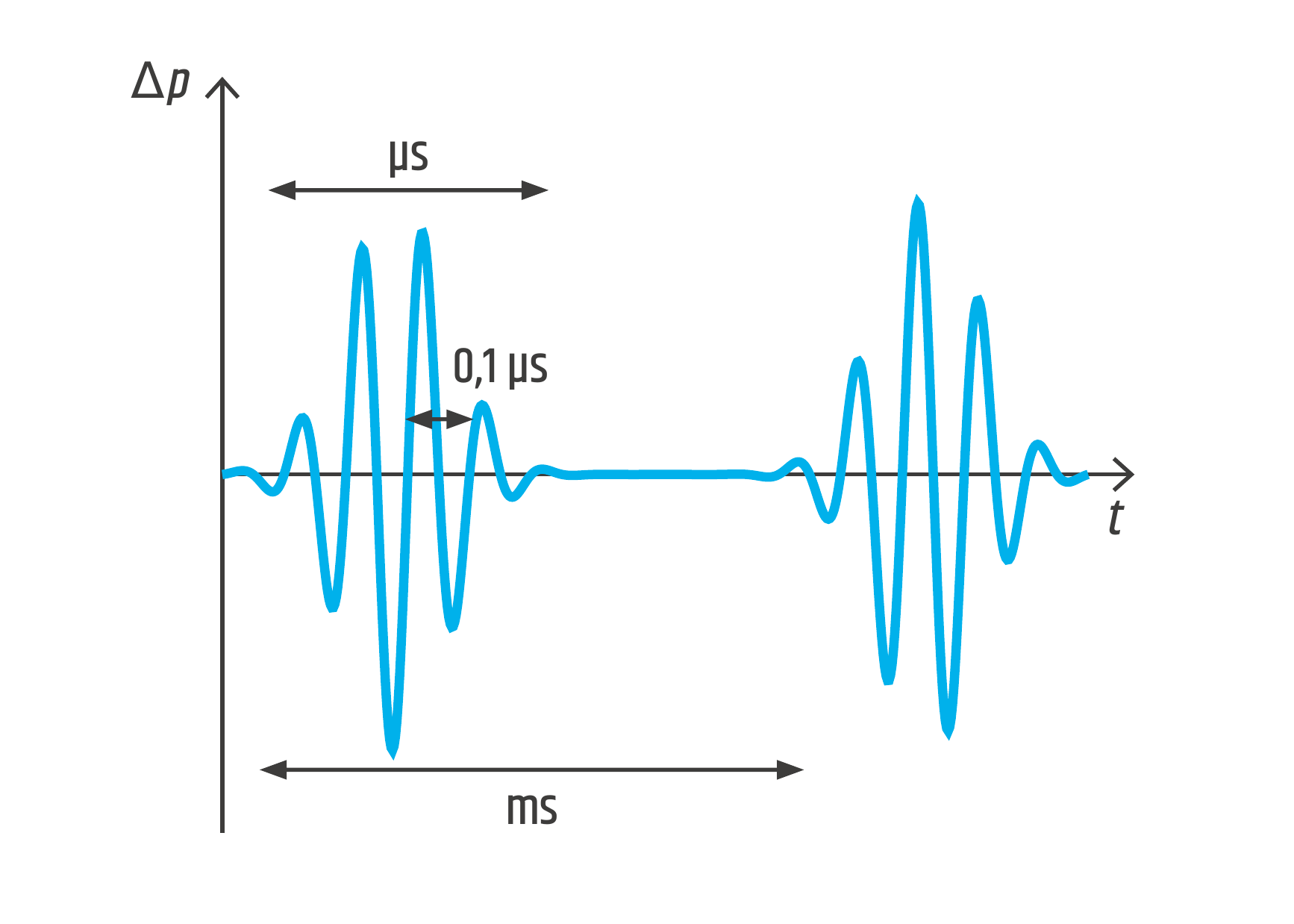
Zdroj

2) \(v = \frac{1{,}5\ \mathrm{cm}}{10\ \mu\mathrm{s}} = 1\,500\ \mathrm{m/s} \)

3a) Když se zvýší frekvence, hloubka zobrazované oblasti se sníží (nepřímá úměrnost).

3b) Když se zvýší frekvence, absolutní nejistota měření délky se zmenší (nepřímá úměrnost).

4) Pro 5,0 MHz: \(T=0{,}2\ \mu\mathrm{s}\) a \(\lambda=0{,}3\ \mathrm{mm}\) pro \(f=5\ \mathrm{MHz}\).

Pro 10 MHz: \(T=0{,}1\ \mu\mathrm{s}\) a \(\lambda=0{,}15\ \mathrm{mm}\) pro \(f=10\ \mathrm{MHz}\).

5) Pro určitou frekvenci je \(\Delta\lambda/\lambda=1\) čili nejistota měření je dána vlnovou délkou použitého vlnění.

6) \( d = v\frac{\Delta t}2 \)

7a) Odražený ultrazvuk musíme zachytit dříve, než sonda začne vysílat následující pulz: \(\Delta t<1\ \mathrm{ms}\), \(d_\mathrm{max}=0{,}75\ \mathrm{m}\).

7b) Odražený ultrazvuk můžeme zaznamenávat až po vyslání celého pulzu: \(\Delta t>1\ \mu\mathrm{s}\), \(d_\mathrm{min}=0{,}75\ \mathrm{mm}\).

8) 11 cm

Cvičení 2

Alpský roh

Problémová úloha – podle maturitního zadání z fyziky, Francie, 2014 (přeloženo a upraveno)

Alpský roh byl kdysi používán pastýři k vzájemnému dorozumívání. Hráč se nachází na vrcholku hory Bec de la Montau. Na svůj alpský roh hraje nejhlubší tón. Délka nástroje je 3,4 m a hladina intenzity zvuku ve vzdálenosti jeden metr od nástroje je 100 dB.

Je možné vzniklý zvuk slyšet v obci Haute Nendaz?

22.87 – Je možné, aby v obci Haute Nendaz bylo slyšet alpský roh pastýře, který se nachází na hoře Bec de la Montau?
Zdroj

22.88 – Mezinárodní setkání hráčů na alpský roh se koná každoročně v červenci ve švýcarské obci Haute Nendaz.
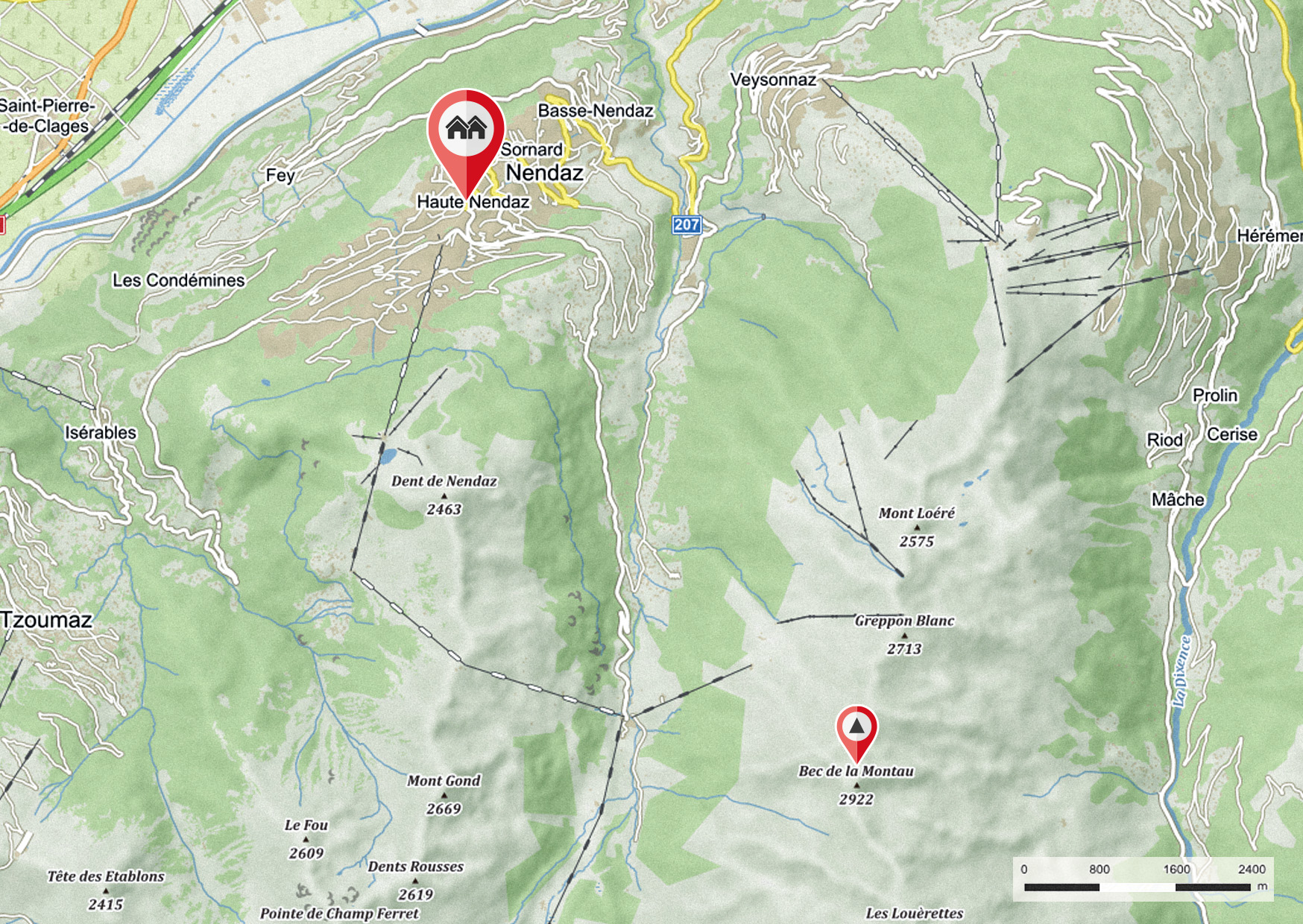
Zdroj

Předpoklady:

Tlumení zvukových vln neuvažujeme – ztráty energie během šíření jsou zanedbatelné.
Nástroj je izotropním zdrojem zvuku – vysílá vlny do všech směrů se stejnou intenzitou.
Zadaná hodnota: Referenční hodnota intenzity zvuku \(I_0=10^{-12}\ \mathrm{W/m}^2\).

Dokument 1: Rychlost šíření zvuku ve vzduchu v závislosti na teplotě

Teplota ve °C	10	20	30	40
Rychlost zvuku v m/s	337	343	349	355

Dokument 2: Alpský roh – dechový hudební nástroj

Když fouknete do alpského rohu poprvé, zdá se téměř nemožné vyloudit z něj jediný hezký tón. Ale po troše tréninku se na něm dá zahrát až dvacet dva not, a to bez jakýchkoli klapek nebo pístů. Řada tónů, které lze na tomto nástroji vytvořit, závisí na jeho geometrii a na nadání hráče. První alpské rohy pocházejí ze 14. století a byly tradičně používány hlídači stád ke komunikaci na vzdálenost kolem deseti kilometrů. Tento nástroj patřící mezi žestě je vyroben z jediného kusu dřeva. Má tvar na jednom konci zahnuté trubice a měří obvykle dva až čtyři metry. Při hraní hráč fouká do nátrubku. Když zní nejhlubší tón, vlnová délka příslušné zvukové vlny je rovna dvojnásobku délky rohu.

22.89 – Alpský roh je vyroben ze dřeva a měří obvykle dva až čtyři metry.
Zdroj

Dokument 3: Intenzita zvuku izotropního zdroje

Izotropní zdroj vysílá vlny do všech směrů se stejnou intenzitou. Je-li jeho celkový akustický výkon \(P\), závisí intenzita zvuku \(I\) na vzdálenosti \(r\) od zdroje podle vztahu.

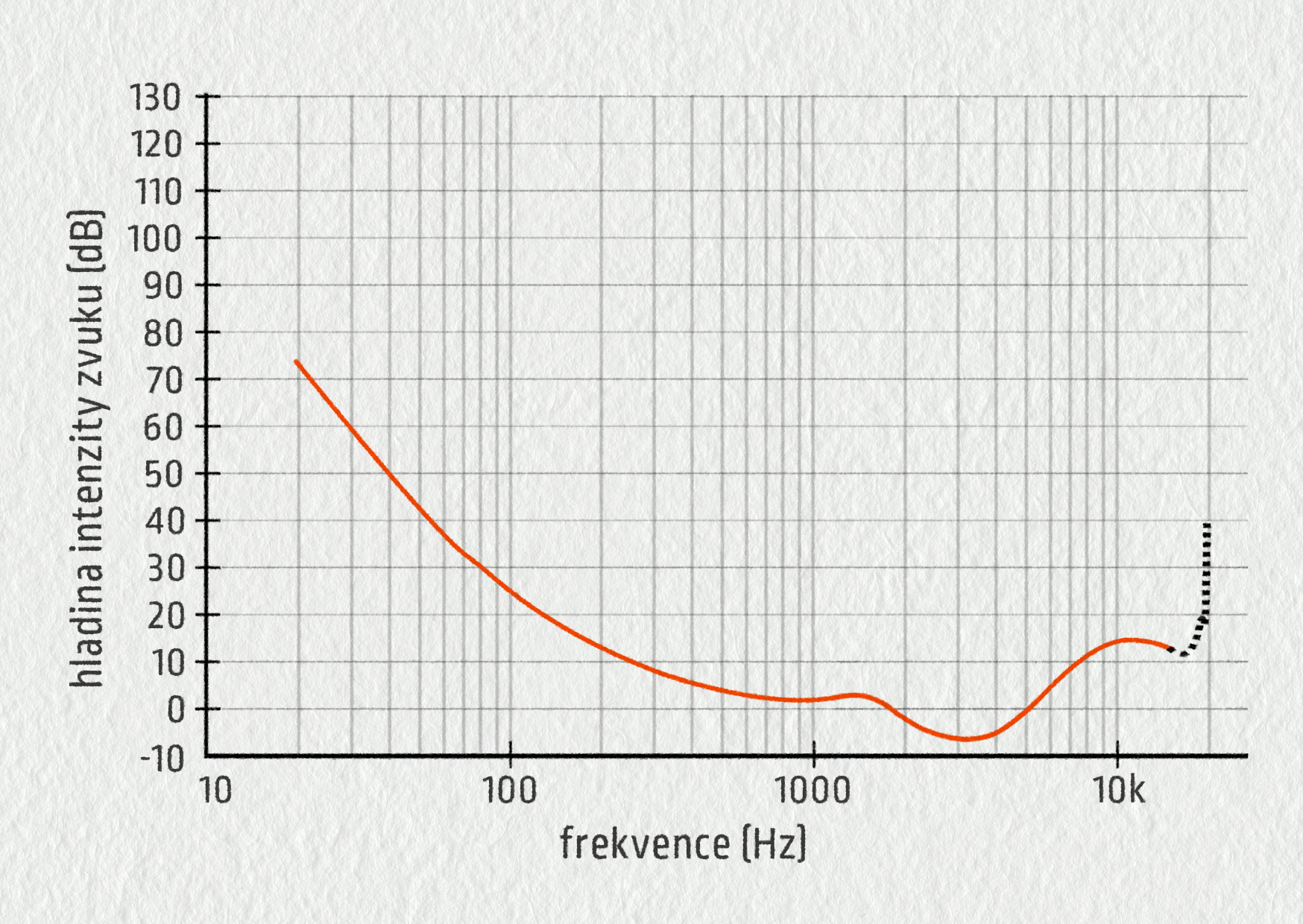
\[ I = \frac{P}{4\pi r^2}\;. \]

Dokument 4: Práh slyšení v závislosti na frekvenci

22.90 – Práh slyšení v závislosti na frekvenci. Graf znázorňuje minimální hodnoty hladiny intenzity zvuku, které je lidský sluch schopen zaregistrovat.
Zdroj

Podle mapy je vzdálenost z vrcholu hory Bec de la Montau do vesnice Haute Nendaz přibližně 7,3 km.

Teplotu v červenci ve švýcarské vysočině odhadujeme na 20 °C.

Vlnová délka základního tónu je 6,8 m a frekvence 51 Hz.

Intenzita zvuku ve vzdálenosti 1,0 m od nástroje je 1,0 ⋅ 10⁻² W/m². Ve vzdálenosti 7,3 km od nástroje má intenzita zvuku hodnotu 1,9 ⋅ 10⁻¹⁰ W/m², což odpovídá hladině intenzity 23 dB.

Podle grafu 22.90 vidíme, že hladina 23 dB je při 51 Hz pod prahem slyšení, a tedy nejhlubší tón slyšet nemůžeme.