V této závěrečné části kapitoly věnované mechanickým vlnám se podrobněji podíváme na fyzikální princip strunných a dechových hudebních nástrojů. Pokusíme se podat vysvětlení, jak tón vzniká, jaké vlastnosti nástroje ovlivňují výšku vytvářeného tónu a jak vše souvisí s hudebními intervaly a laděním.
Strunné hudební nástroje
Vlnění na struně
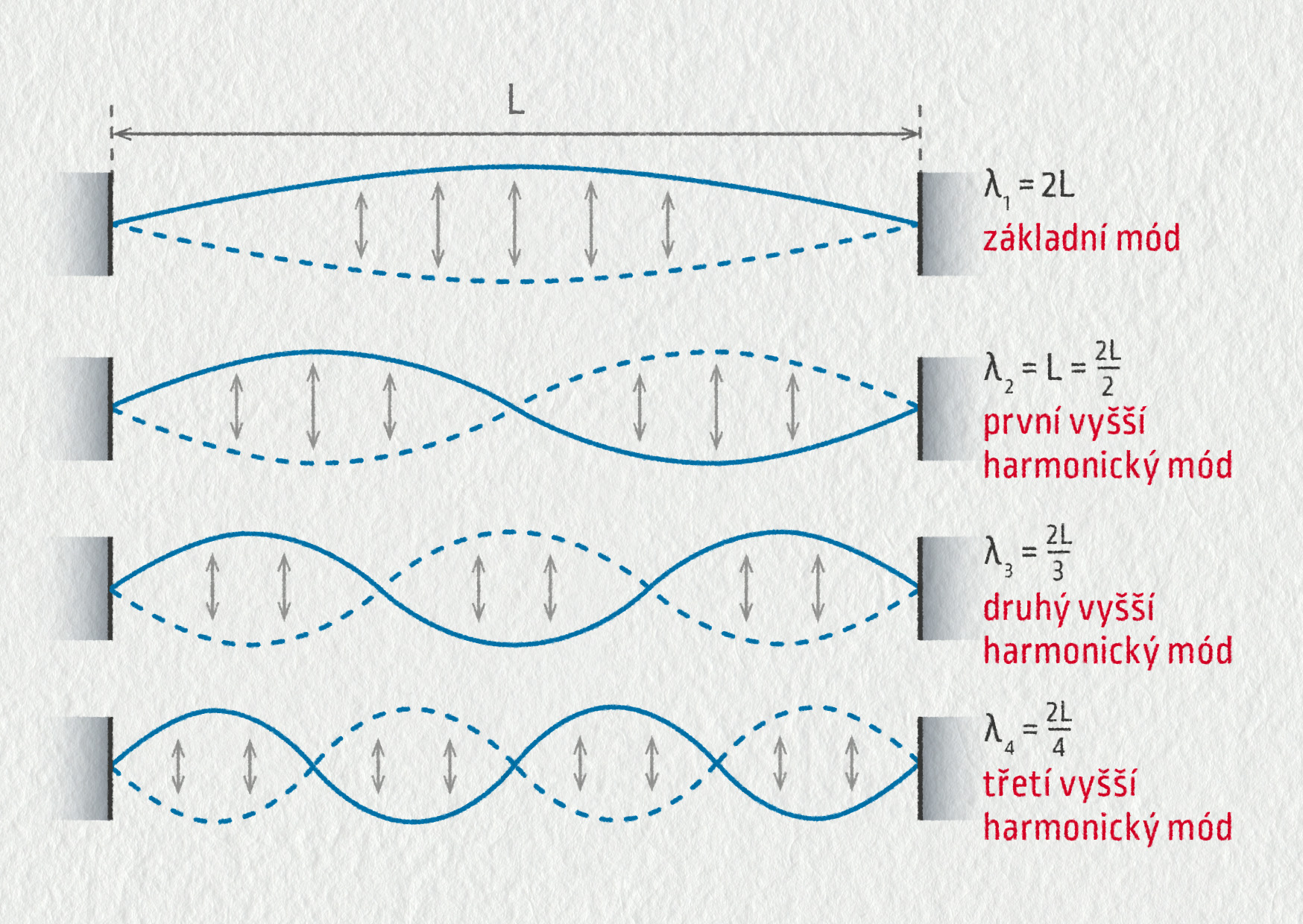
Uvažujme strunu napjatou mezi dvěma pevnými konci – jejich vzdálenost budeme značit \(L\). Strunu bychom mohli chápat jako těleso kmitající s určitou frekvencí, ale k vysvětlení hlubších souvislostí je výhodné se na ni dívat jako na pružné prostředí, kterým se mohou šířit vlny. Přesněji řečeno, po počátečním impulzu (brnknutí) se strunou šíří příčná mechanická vlna až k okraji (pražec, kobylka), kde se odráží, a odražená vlna interferuje s původní přímou vlnou. Tím vzniká na struně stojaté vlnění s uzly a kmitnami. Je zřejmé, že pevné konce představují vždy uzly stojaté vlny. Obrázek 22.66 znázorňuje první čtyři vibrační módy struny (mód znamená způsob, jakým může dané těleso kmitat). Všimněte si, že kvůli upevnění struny na koncích nemůže vlnová délka stojaté vlny nabývat libovolných hodnot, ale je dána podmínkou \(\lambda_k=2L/k\), kde \(k=1,2,3,\dots\) je řád vibračního módu.
Zdroj
Vlnová délka souvisí s frekvencí vztahem \(\lambda=v/f\), takže frekvence vydávaná strunou kmitající v základním módu je \(f_1=v/\lambda_1=v/(2L)\). Při kmitání v \(k\)-tém módu bude tato struna vydávat zvuk o frekvenci
\[ f_k = \frac v{\lambda_k} = \frac{v}{2L}k = kf_1\;. \]Zjišťujeme tedy velice zajímavou věc: struna může vydávat jen zvuk o frekvencích, které jsou celočíselným násobkem základní frekvence \(f_1\). Základní frekvence \(f_1\) je dána jednoznačně délkou struny \(L\) a rychlostí \(v\) šíření vlnění na struně. Frekvencím \(f_2=2f_1\), \(f_3=3f_1\), … se říká vyšší harmonické frekvence. Ve skutečnosti mohou vibrace v různých kmitových módech probíhat současně – prostě se skládají, takže reálná struna vydává zároveň více frekvencí daných předchozí podmínkou.
Podle základní frekvence \(f_1=v/(2L)\) identifikuje lidský sluch výšku tónu. Amplitudy vyšších harmonických frekvencí (módů) určují barvu tónu.
Výška tónu vydávaného strunou
Výška tónu je určena pomocí základní frekvence kmitání \(f_1=v/(2L)\).
V tomto vztahu představuje \(L\) aktivní délku struny – je to ta část struny, která kmitá. Čím je tato aktivní délka větší, tím hlubší tón zní. U některých nástrojů existuje pro každý tón samostatná struna (klavír), u jiných (kytara, housle) může hráč aktivní délku zkrátit stiskem struny v určitém místě a tím zvýšit vydávaný tón.
Rychlost šíření vlnění \(v\) na struně závisí na napínací síle \(F\) a lineární hustotě struny \(\mu\) (hmotnost na jednotku délky). Dá se odvodit, že \(v=\sqrt{F/\mu}\). Lineární hustota struny je dána při její výrobě a hráč ji nemůže ovlivnit. Struny pro vysoké tóny bývají tenké a lehké (malá hodnota \(\mu\)), struny pro hluboké tóny těžké a často spletené z více vláken.
Napínací sílu \(F\) může hráč ovlivnit utahováním nebo povolováním ladicího kolíku, na nějž je struna na jednom konci navinuta. Se zvětšováním napínací síly \(F\) se zvyšuje rychlost šíření vlnění na struně \(v\), což vede ke vzrůstu základní frekvence \(f_1\), tedy k vyššímu tónu.

Zdroj
Rozezvučení struny
Podle způsobu rozezvučení dělíme strunné nástroje na smyčcové, drnkací a úderové.
U drnkacích (kytara, banjo, ukulele, cembalo…) a úderových (klavír, cimbál) po počátečním impulzu vykonává struna volné tlumené kmity.
Fyzikálně zajímavější je hra pomocí smyčce. Vlákna smyčce se statickým třením zachytí o strunu a pohybem do strany ji vychylují. V okamžiku, kdy vratná síla struny (roste s výchylkou) převýší maximální sílu statického tření, začne struna klouzat zpět k rovnovážné poloze, tedy proti směru pohybu smyčce. V tomto případě jde o tření dynamické s nižším součinitelem smykového tření. Jakmile dojde k opětovnému zachycení, situace se opakuje. Jedná se tedy o příklad nuceného kmitání, v němž je smyčec budičem a struna rezonátorem s velmi ostrým rezonančním maximem.

Zdroj
Tělo nástroje jako rezonátor
Tenká kmitající struna má malý povrch a je v kontaktu s relativně malým objemem vzduchu. Samotná by tedy vydávala jen těžko slyšitelný zvuk, asi jako když brnknete na provázek upnutý mezi dva háčky. Proto musí být strunný hudební nástroj opatřen rezonanční deskou nebo skříní s velkým povrchem. Přes upevnění se kmity struny přenáší na tuto rezonanční desku, která rozkmitá velký objem vzduchu.
V tomto případě je struna budičem a rezonanční deska rezonátorem. Fyzikálně se jedná o rezonátor se silným tlumením, jehož rezonanční křivka má velmi široké maximum. Znamená to, že nízké i vysoké frekvence vydávané strunou jsou rezonátorem „zesilovány“ přibližně stejně.

Zdroj
Dechové hudební nástroje
Vznik vlnění v dechovém nástroji
Zvuk vzniká foukáním vzduchu do nástroje, který funguje jako rezonátor.
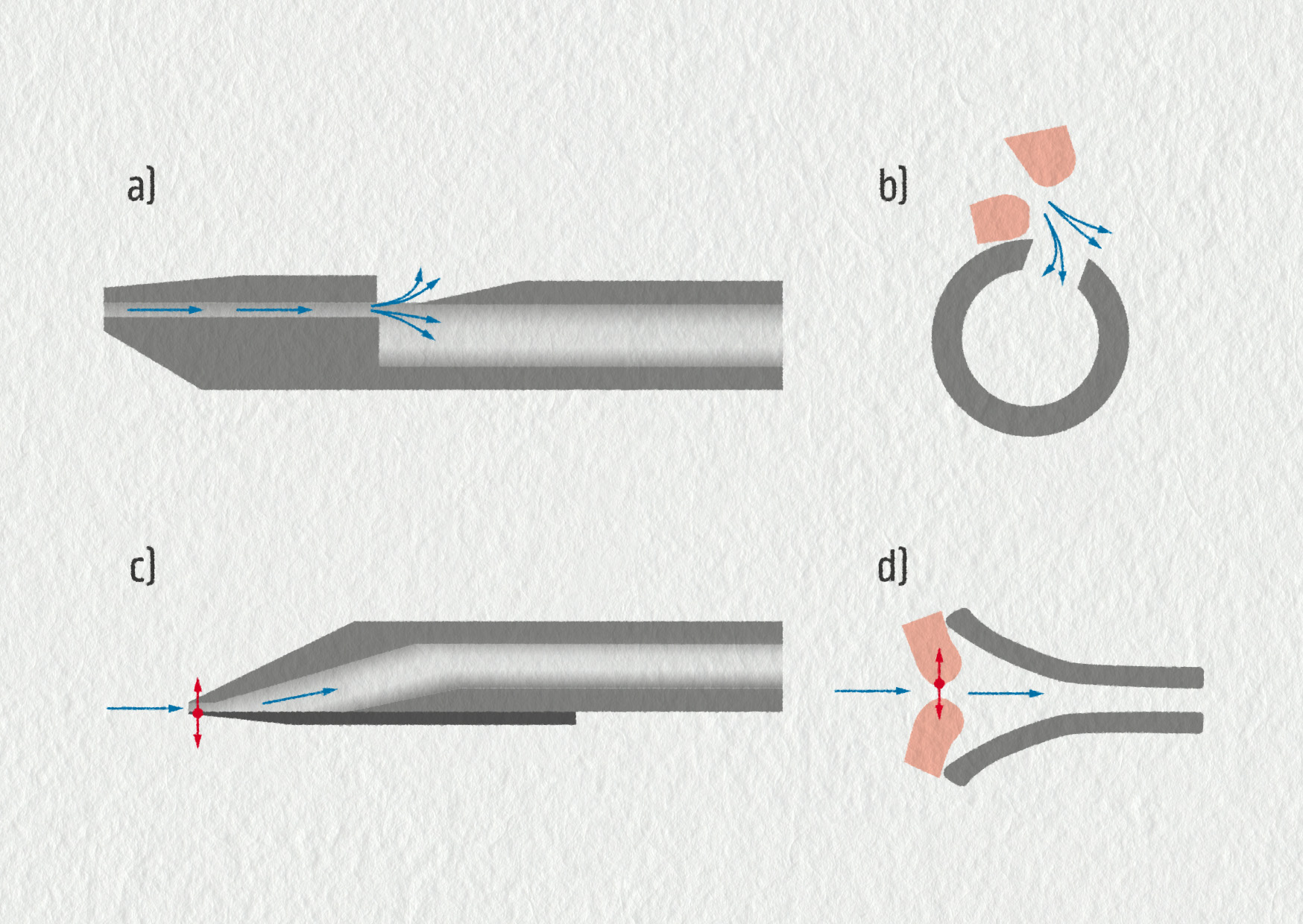
Dechové hudební nástroje se klasicky dělí na dřevěné (píšťaly, plátkové, …) a žesťové. U píšťal a fléten dopadá proud vzduchu hráče na ostrou hranu na okraji trubice, na hraně vzniká turbulentní proudění, jímž se rozechvěje sloupec vzduchu v nástroji. U klarinetu a hoboje (plátkové nástroje) zvukové vlny vytváří proud vzduchu, který rozkmitá plátek sevřený mezi rty. Kmitání plátku v proudu vzduchu vytváří tlakové vlny uvnitř ozvučné trubice. Podobné je to i v případě žesťových nástrojů. Hráč fouká vzduch mezi napjaté sevřené rty opřené o nátrubek. Mezi rty pravidelně vzniká štěrbina, kterou pokaždé projde malé množství vzduchu, vzniklé tlakové vlny rozechvívají vzduchový sloupec v nástroji.
Zdroj
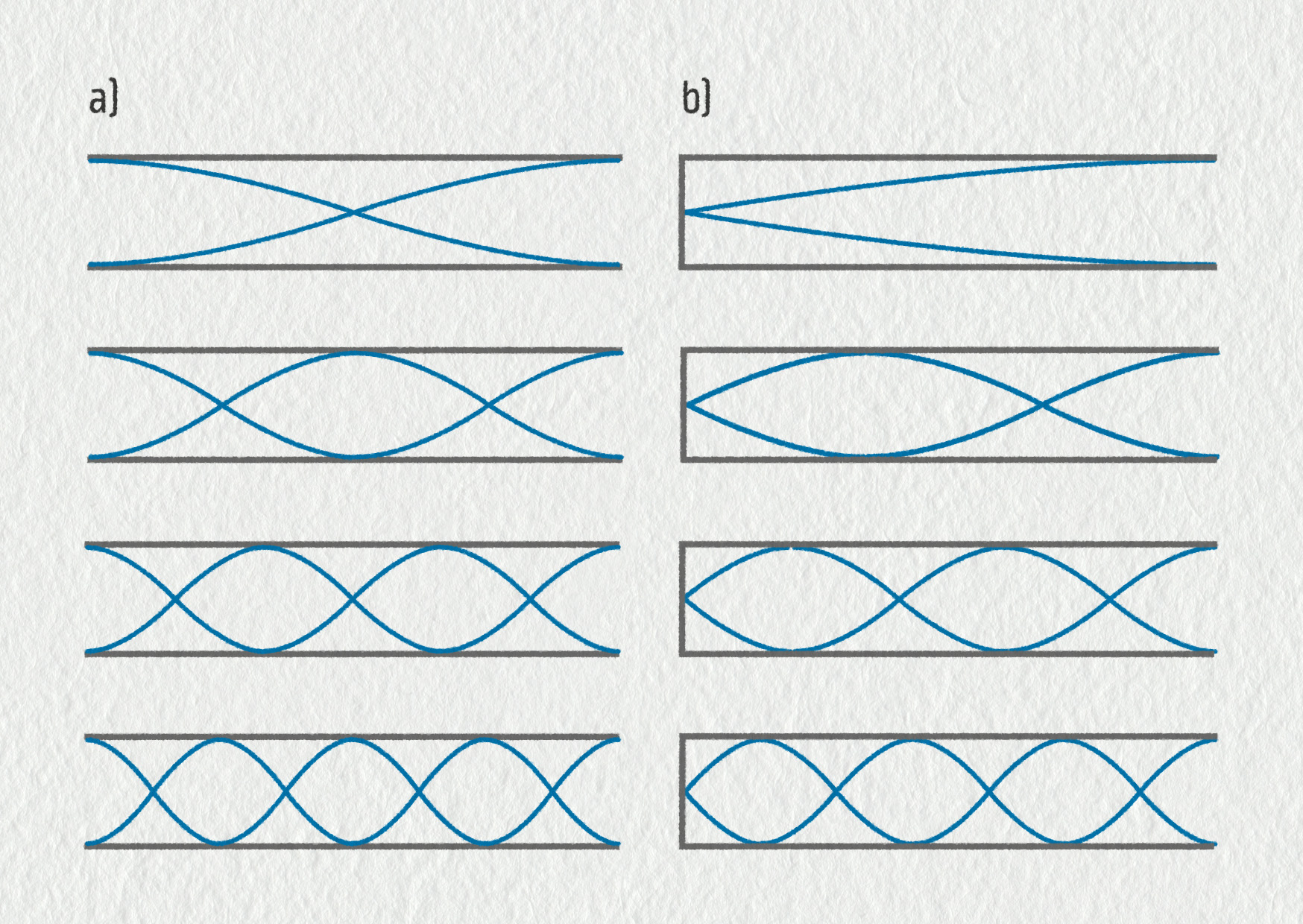
Tělo samotného dechového nástroje je pouhá dutá trubice válcového nebo kuželovitého tvaru vyplněná vzduchem. Na jednom konci hráč svým dechem vzduch rozkmitává, trubicí se šíří podélné vlnění k druhému (otevřenému) konci, kde se odráží a skládá s vlnou přímou. Ve vzduchu uvnitř nástroje tak vzniká podélné stojaté vlnění. Toto stojaté vlnění má vždy uzel na uzavřeném konci a kmitnu na konci otevřeném – viz obrázek 22.71. Podobně jako u struny, délka dechového nástroje tedy určuje přípustné vlnové délky, potažmo frekvence, jež mohou v nástroji existovat. Jinými slovy, trubice funguje jako rezonátor s velmi ostrými rezonančními maximy. Ze všech možných frekvencí vydávaných např. vibrujícími rty se rozezní jen ty, které splňují podmínku danou délkou nástroje, všechny ostatní frekvence se utlumí.
Zdroj
V případě píšťaly (rezonátor s oběma konci otevřenými, viz obrázek 22.71 a) splňují přípustné vlnové délky stejnou podmínku jako na struně, totiž \(\lambda_k=2L/k\), kde \(L\) je délka trubice a \(k=1,2,3,\dots\) je řád vibračního módu. S využitím vztahu pro frekvenci \(f=v/\lambda\) můžeme snadno odvodit podobné závěry jako pro strunné nástroje:
- základní frekvence určující výšku tónu je dána vztahem \(f_1=v/(2L)\), kde \(v\) je rychlost šíření zvuku ve vzduchu uvnitř nástroje,
- v trubici nástroje existují i vlny s frekvencemi \(f_k=kf_1\), kde \(k=2,3,4,\dots\) (tzv. vyšší harmonické frekvence), jejichž zastoupení dává zvuku nástroje charakteristickou barvu.
Výška tónu dechového nástroje
Výšku tónu určuje délka rezonujícího vzduchového sloupce \(L\). Mohli bychom pro každý tón ve stupnici vyrobit trubici jiné délky (varhany, Panova flétna, skleněné varhany v motivační aktivitě), ale existují i jiná řešení. U dřevěných nástrojů (píšťaly a flétny, klarinet, hoboj, …) lze efektivní délku \(L\) ozvučné trubice zmenšovat odkrýváním dírek v nástroji – to vede ke zvýšení tónu. U žesťových nástrojů (trubka, lesní roh, tuba, …) se efektivní délka ozvučné trubice prodlužuje připojováním „odboček“ nebo vysouváním snižce, jak je tomu u trombonu. To vede ke snížení tónu.
Výška tónu závisí také na rychlosti šíření zvuku ve vzduchu uvnitř nástroje, a tím pádem na jeho teplotě: při zvýšení teploty vzduchu v nástroji vzroste i výška hraného tónu.
Zdroj

Zdroj
Dechové nástroje mají ještě jednu vymoženost, jak změnit výšku tónu – tak zvané přefukování. Při silnějším proudu vzduchu může hráč vytvořit v nástroji proudění s vyšší frekvencí, než je základní frekvence \(f_1\) ozvučné trubice. V tom případě se kmitání s frekvencí \(f_1\) nevybudí, a naopak se rozezní některá z vyšších harmonických frekvencí (a její násobky). Jedná se o zcela běžnou techniku hry. Hráčovo umění spočívá v přizpůsobení množství vzduchu a napětí rtů tak, aby se vytvořenými turbulencemi právě „strefil“ do správného vibračního módu rezonujícího vzduchového sloupce.
Posloupnost tónů, které lze na dechovém nástroji vytvořit pouhým přefukováním, se nazývá alikvotní tóny a je základem hudebních intervalů a čistého ladění.

Zdroj
Čisté a temperované ladění
Hudební intervaly
Hudební interval je vzdálenost mezi dvěma tóny na výškové škále. Lidský sluch vnímá jako libozvučné intervaly mezi tóny, jejichž frekvence jsou v poměru malých celých čísel – viz následující tabulka.
| Interval | Poměr frekvencí | Příklad ve stupnici C dur |
|---|---|---|
| prima | 1 : 1 | c1–c1 |
| oktáva | 2 : 1 | c1–c2 |
| kvinta | 3 : 2 | c1–g1 |
| kvarta | 4 : 3 | c1–f1 |
| velká tercie | 5 : 4 | c1–e1 |
| malá tercie | 6 : 5 | e1–g1 |
| velká sexta | 5 : 3 | c1–a1 |
| velká sekunda | 9 : 8 | c1–d1 |
Tyto intervaly vznikají přirozeně mezi frekvencemi jednotlivých vibračních módů struny nebo vzduchového sloupce v píšťale. Definují tak čisté (přirozené) ladění.
Tón a1 má frekvenci 440 Hz (komorní a). Jakou frekvenci má tón a2 o oktávu vyšší? Napište číselnou hodnotu frekvence v hertzech Hz.
Tón a1 má frekvenci 440 Hz (komorní a). Tón e1 je o kvartu nižší než tón a1. Jakou má frekvenci tón e1? Napište číselnou hodnotu frekvence v hertzech Hz.
Poměr frekvencí odpovídající kvartě je 4 : 3. Tedy \(f_\mathrm{a^1}/f_\mathrm{e^1}=4/3\).
Jedna oktáva odpovídá zvýšení frekvence na dvojnásobek, čili e2 má frekvenci \(2\cdot330\ \mathrm{Hz}=660\ \mathrm{Hz}\) a e3 má frekvenci \(2\cdot660\ \mathrm{Hz}=1\,320\ \mathrm{Hz}\).
Temperované ladění
Z přirozených intervalů bychom mohli sestavit stupnici a hrát v čistém ladění jako v období renesance. Skladba by zněla dokonale, pokud bychom trvale zůstávali v tónině, na kterou máme naladěný nástroj. Problém nevyhnutelně nastane, pokud skladba přejde do jiné tóniny. Například Bachovo Preludium č. 1 by znělo na klavíru v čistém ladění do C dur takto:
https://upload.wikimedia.org/wikipedia/commons/4/49/Prelude_1%2C_Just_intonation.ogg
Aby byly všechny tóniny rovnocenné a skladba zahraná od různých tónů zněla vždy stejně čistě, používá se v Evropě již od doby baroka temperované ladění. Interval oktávy (poměr frekvencí 2 : 1) se rozdělí na dvanáct stejně velkých půltónů. Jeden půltón tedy odpovídá poměru frekvencí \(^{12}\sqrt{2}:1=1{,}05946:1\). V tomto rovnoměrně temperovaném ladění například interval kvarty odpovídá pěti půltónům a poměr frekvencí není přesně \(4:3=1{,}\bar3:1\), nýbrž \((^{12}\sqrt{2})^5:1=1{,}3348:1\). Výsledek můžete sluchově posoudit na téže skladbě – Bachovo Preludium č. 1 zahrané na dobře temperovaný klavír:
https://upload.wikimedia.org/wikipedia/commons/e/eb/Prelude_1%2C_Equal_temperament.ogg
Tón a1 (komorní a) má frekvenci 440 Hz. Jakou frekvenci má v temperovaném ladění tón c2?

Zdroj
V obrázku 22.75 vidíme, že c2 je od a1 vzdáleno o jeden a půl tónu, tzn. o tři půltóny. Poměr jejich frekvencí je \((^{12}\sqrt{2})^3\), tedy frekvence tónu c2 je \((^{12}\sqrt{2})^3\)-krát vyšší než frekvence tónu a1.
Frekvence tónu c2 je \((^{12}\sqrt{2})^3\cdot440\ \mathrm{Hz}=523\ \mathrm{Hz}\).

